鲁教版数学七年级下册 11.5 一元一次不等式与一次函数( 第2课时)课件 (共14张PPT)
文档属性
| 名称 | 鲁教版数学七年级下册 11.5 一元一次不等式与一次函数( 第2课时)课件 (共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 11:01:37 | ||
图片预览





文档简介
(共14张PPT)
5 一元一次不等式与一次函数 (第2课时)
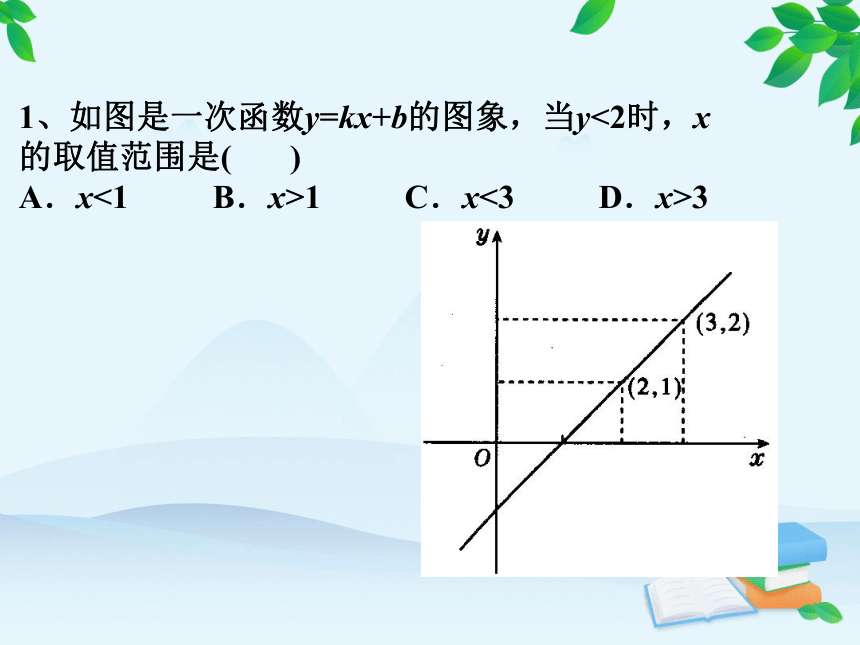
1、如图是一次函数y=kx+b的图象,当y<2时,x
的取值范围是( )
A.x<1 B.x>1 C.x<3 D.x>3
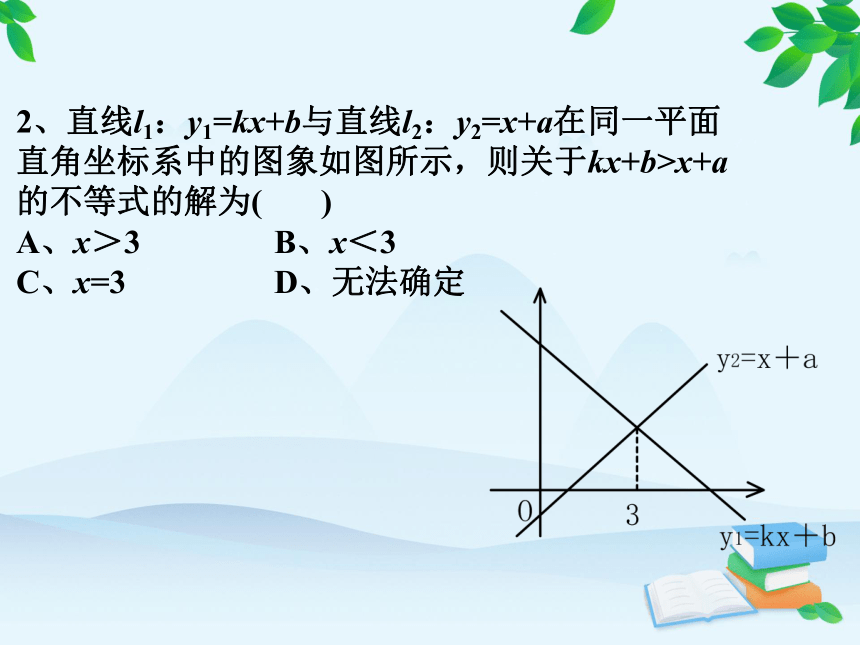
2、直线l1:y1=kx+b与直线l2:y2=x+a在同一平面
直角坐标系中的图象如图所示,则关于kx+b>x+a
的不等式的解为( )
A、x>3 B、x<3
C、x=3 D、无法确定
某电信公司有甲、乙两种手机收费业务.甲种业务规定月租费10元,每通话1 min收费0.3 元;乙种业务不收月租费,但每通话1min收费0.4 元.你认为何时选择甲种业务对顾客更合算?何时选择乙种业务对顾客更合算?
解:设顾客每月通话时长为x min,那么甲种业务每个月的消费额为y1,乙种业务每个月的消费额为y2,根据题意可知
y1=10+0.3x y2=0.4x
当甲乙两种业务消费额 一样时
即y1= y2,得10+0.3x=0.4x,解得x=100;
当甲乙两种业务消费额不一样时,
①由y1>y2,得10+0.3x>0.4x,解得x<100;
此时选择乙种业务比较合算.
②由y1100.
此时选择甲种业务比较合算.
所以当顾客每个月的通话时长等于100 min时,选择甲乙两种业务一样合算;如果通话时长大于100 min,选择甲种业务比较合算;如果通话时长小于100 min,选择乙种业务比较合算.
方案选择问题解题思路:
(1)根据题意分别写出方案A、B的函数解析式yA、yB;
(2)将方案A、B进行比较:①yA>yB , ②yA(3)根据实际情况选择方案。
某公司40名员工到一景点集体参观,该景点规定满40人可以购买团体票,票价打八折。这天恰逢妇女节,该景点做活动,女士票价打五折,但不能同时享受两种优惠。请你帮助他们选择购票方案。
解:设该公司参观者中有女士x人,选择购买女士五折票时所需费用为y1元,选择购买团体票时所需费用为y2元,则
由y1 = y2,得0.5x+40-x=40×0.8,解得x=16
由y1 > y2,得0.5x+40-x>40×0.8 ,解得x<16
由y1 < y2,得0.5x+40-x<40×0.8 ,解得x>16
答:当女士不足16人时,购买团体票合算;当女士恰好是16人时,两种方案所需费用相同;当女士多于16人时,购买女士五折票合算。
例1 某单位要制作一批宣传材料。甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费。
(1)什么情况下选择甲公司比较合算
(2)什么情况下选择乙公司比较合算
(3)什么情况下两公司的收费相同
(1)当制作材料超过300份时,选择甲公司比较合算;
(2)当制作材料少于300份时,选择乙公司比较合算;
(3)当制作材料为300份时,两公司收费相同。
例2 某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为6000元,并且多买都有一定的优惠。
甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%。
(1)什么情况下到甲商场购买更优惠?
(2)什么情况下到乙商场购买更优惠?
(3)什么情况下两家商场的收费相同?
例3 某乳品公司向某地运输一批牛奶,由铁路运输每千克需运费0.58元,由公路运输,每千克需运费0.28元,另需补贴600元。
(1)设该公司运输的这批牛奶为xkg,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1 、y2与x之间的关系式;
(2)若公司支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500kg牛奶,则选用哪种运输方式所需费用较少?
例4 红枫湖门票是每位45元,20人以上(包含20人)的团体票七五折优惠,现在有18位游客买20人的团体票
(1)比买普通票总共便宜多少钱?
(2)不足20人时,多少人买20人的团体票才比普通票便宜?
解决实际问题步骤:
(1)理清题目中的数量关系,把这些数量关系分解为几个函数关系;
(2)列出这些函数关系式;
(3)根据题意,将列出的函数关系式转化为不等式;
(4)解不等式;
(5)选择符合题意的不等式的解集.
5 一元一次不等式与一次函数 (第2课时)
1、如图是一次函数y=kx+b的图象,当y<2时,x
的取值范围是( )
A.x<1 B.x>1 C.x<3 D.x>3
2、直线l1:y1=kx+b与直线l2:y2=x+a在同一平面
直角坐标系中的图象如图所示,则关于kx+b>x+a
的不等式的解为( )
A、x>3 B、x<3
C、x=3 D、无法确定
某电信公司有甲、乙两种手机收费业务.甲种业务规定月租费10元,每通话1 min收费0.3 元;乙种业务不收月租费,但每通话1min收费0.4 元.你认为何时选择甲种业务对顾客更合算?何时选择乙种业务对顾客更合算?
解:设顾客每月通话时长为x min,那么甲种业务每个月的消费额为y1,乙种业务每个月的消费额为y2,根据题意可知
y1=10+0.3x y2=0.4x
当甲乙两种业务消费额 一样时
即y1= y2,得10+0.3x=0.4x,解得x=100;
当甲乙两种业务消费额不一样时,
①由y1>y2,得10+0.3x>0.4x,解得x<100;
此时选择乙种业务比较合算.
②由y1
此时选择甲种业务比较合算.
所以当顾客每个月的通话时长等于100 min时,选择甲乙两种业务一样合算;如果通话时长大于100 min,选择甲种业务比较合算;如果通话时长小于100 min,选择乙种业务比较合算.
方案选择问题解题思路:
(1)根据题意分别写出方案A、B的函数解析式yA、yB;
(2)将方案A、B进行比较:①yA>yB , ②yA
某公司40名员工到一景点集体参观,该景点规定满40人可以购买团体票,票价打八折。这天恰逢妇女节,该景点做活动,女士票价打五折,但不能同时享受两种优惠。请你帮助他们选择购票方案。
解:设该公司参观者中有女士x人,选择购买女士五折票时所需费用为y1元,选择购买团体票时所需费用为y2元,则
由y1 = y2,得0.5x+40-x=40×0.8,解得x=16
由y1 > y2,得0.5x+40-x>40×0.8 ,解得x<16
由y1 < y2,得0.5x+40-x<40×0.8 ,解得x>16
答:当女士不足16人时,购买团体票合算;当女士恰好是16人时,两种方案所需费用相同;当女士多于16人时,购买女士五折票合算。
例1 某单位要制作一批宣传材料。甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费。
(1)什么情况下选择甲公司比较合算
(2)什么情况下选择乙公司比较合算
(3)什么情况下两公司的收费相同
(1)当制作材料超过300份时,选择甲公司比较合算;
(2)当制作材料少于300份时,选择乙公司比较合算;
(3)当制作材料为300份时,两公司收费相同。
例2 某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为6000元,并且多买都有一定的优惠。
甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%。
(1)什么情况下到甲商场购买更优惠?
(2)什么情况下到乙商场购买更优惠?
(3)什么情况下两家商场的收费相同?
例3 某乳品公司向某地运输一批牛奶,由铁路运输每千克需运费0.58元,由公路运输,每千克需运费0.28元,另需补贴600元。
(1)设该公司运输的这批牛奶为xkg,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1 、y2与x之间的关系式;
(2)若公司支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500kg牛奶,则选用哪种运输方式所需费用较少?
例4 红枫湖门票是每位45元,20人以上(包含20人)的团体票七五折优惠,现在有18位游客买20人的团体票
(1)比买普通票总共便宜多少钱?
(2)不足20人时,多少人买20人的团体票才比普通票便宜?
解决实际问题步骤:
(1)理清题目中的数量关系,把这些数量关系分解为几个函数关系;
(2)列出这些函数关系式;
(3)根据题意,将列出的函数关系式转化为不等式;
(4)解不等式;
(5)选择符合题意的不等式的解集.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
