鲁教版数学七年级下册 8.6三角形内角和定理 (第1课时) 课件 (共18张PPT)
文档属性
| 名称 | 鲁教版数学七年级下册 8.6三角形内角和定理 (第1课时) 课件 (共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 11:05:59 | ||
图片预览




文档简介
(共18张PPT)
5 三角形内角和定理
第1课时
1
A
B
D
2
3
C
如图,我们把∠A移到了∠1的
位置,∠B移到了∠2的位置.就得到
了三角形三个内角的和等于
180°.
根据前面的公理和定理,你能用自己的语言说说这一结论的证明思路吗 你能用比较简捷的语言写出这一证明过程吗 与同伴交流.
情境导入
已知:如图,△ABC.
求证:∠A+∠B+∠C=180°.
分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
A
B
C
知识讲解
证明:作BC的延长线CD,过点C作射线CE∥AB,则
∠1=∠A(两直线平行,内错角相等),
∠2= ∠B(两直线平行,同位角相等).
又∵∠1+∠2+∠3= 180° (平角的定义),
∴∠A+∠B+∠ACB= 180° (等量代换).
你还有其他方法来证明三角形内角和定理吗
这里的CD,CE称为辅助线,辅助线通常画成虚线.
A
B
C
E
2
1
3
D
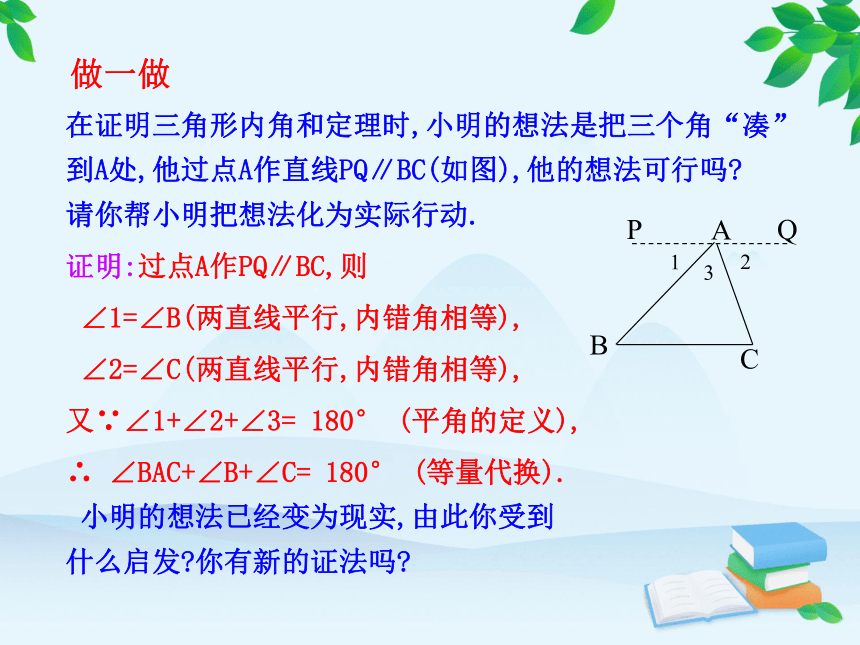
在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可行吗
请你帮小明把想法化为实际行动.
证明:过点A作PQ∥BC,则
∠1=∠B(两直线平行,内错角相等),
∠2=∠C(两直线平行,内错角相等),
又∵∠1+∠2+∠3= 180° (平角的定义),
∴ ∠BAC+∠B+∠C= 180° (等量代换).
小明的想法已经变为现实,由此你受到
什么启发 你有新的证法吗
A
B
C
P
Q
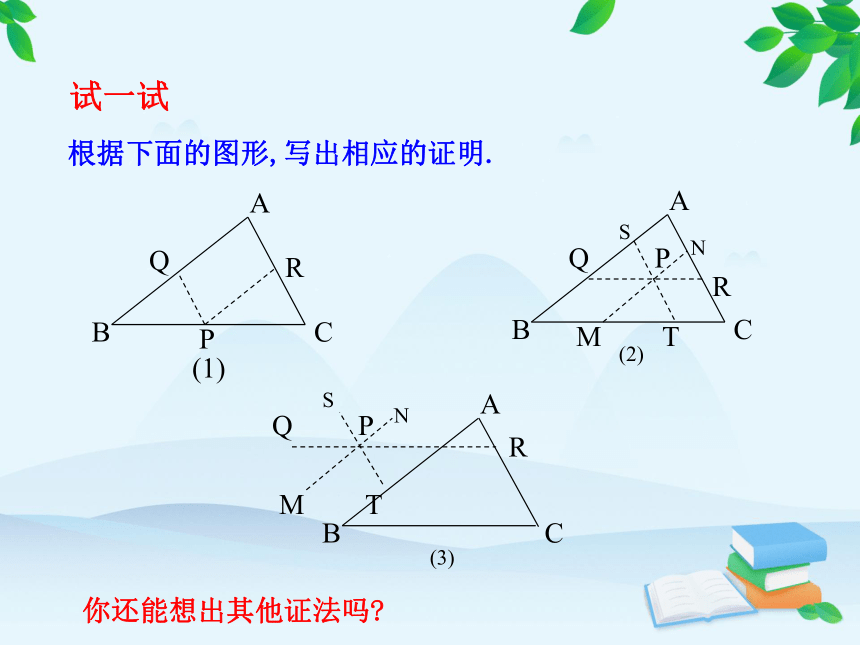
做一做
2
3
1
根据下面的图形,写出相应的证明.
你还能想出其他证法吗
(1)
A
B
C
P
Q
R
T
S
N
(3)
A
B
C
P
Q
R
M
T
S
N
(2)
A
B
C
P
Q
R
M
试一试
A
C
B
图1
B
A
C
图2
B A
C
图3
BAC
图4
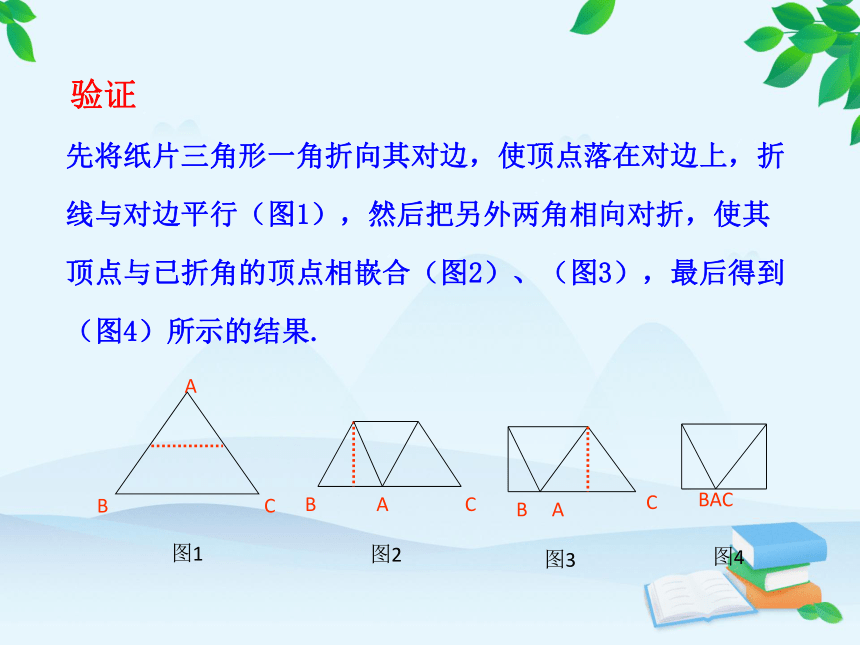
先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另外两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果.
验证
C
B
A
如果BC不动,把点A“拉离”BC,
那么当点A越来越远离BC时,∠A就
越来越小(越来越接近0°),而
∠B和∠C则越来越大,它们的和
越来越接近180°, 当把点A拉
到无穷远时,便有AB∥AC,∠B和
∠C成为同旁内角,它们的和等于180°.由此你能想到什么
读一读
C
B
A
在△ABC中,如果BC不动,把点A“压”向BC,那么当点A越来越接近BC时, ∠A就越来越大(越来越接近180°),而∠B和∠C越来越小(越来越接近0°).由此你能想到什么
用橡皮筋构成△ABC,其中顶点B,C为定点,A为动点,放松橡皮筋后,点A自动收缩于BC上,请同学们考察点A变化时所形成的一系列的三角形,其内角会产生怎样的变化呢?
当点A远离BC时,∠A越来越趋近于0°,而AB与AC逐渐趋向平行,这时,∠B,∠C逐渐接近为互补的同旁内角,即∠B+∠C接近于180°.
试一试
结论
1.(昆明·中考)如图所示,
在△ABC中,CD是∠ACB的平分线,
∠A=80°,∠B=60°,
那么∠BDC=( )
A.80° B.90°
C.100° D.110°
练一练
2.(济宁·中考)若一个三角形三个内角度数的比为2∶3∶4,那么这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
【解析】选B.由题意可设这个三角形的三个内角度数分别
为2x,3x,4x,根据三角形内角和定理可得:2x+3x+4x=180°,
得x=20°,因此可得三个内角度数分别为40°,60°,80°.
3.(红河·中考) 如图,D,E分别是AB,AC上的点,若∠A=70°,∠B=60°,DE∥BC,则∠AED的度数是____.
【解析】因为∠A=70°,∠B=60°,所以∠C=50°,
又因为DE//BC,所以∠AED=∠C=50°.
答案:50°
4.(郴州·中考) 如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=___度.
【解析】如图,根据题意可知∠5=90°,
∴∠3+∠4=90°,
∴∠1+∠2=180°+180°-(∠3+∠4)
=360°-90°=270°.
答案:270
5. 如图,在△ABC中,∠A=60°,
∠B=70°,∠ACB的平分线交AB于D,
DE∥BC交AC于E,求∠EDC和∠BDC的
度数.
【解析】∵∠A=60°,∠B=70°,∴∠ACB=180°-60°
-70°=50°,∵CD是∠ACB的平分线,
∴∠ACD=∠BCD=25°,∵DE∥BC,∴∠EDC=∠BCD=25°.
在△BCD中,∠B=70°,∠BCD=25°,
∴∠BDC=180°-70°-25°=85°.
通过本课时的学习,需要我们掌握:
1.三角形的内角和是180°.
2.证明三角形内角和是180°,不仅可以通过实验操作验证,还可以通过严密的推理得到证明.通过平行线将三个内角拼在一起,得到一个平角或构造同旁内角是常用方法.
小结
5 三角形内角和定理
第1课时
1
A
B
D
2
3
C
如图,我们把∠A移到了∠1的
位置,∠B移到了∠2的位置.就得到
了三角形三个内角的和等于
180°.
根据前面的公理和定理,你能用自己的语言说说这一结论的证明思路吗 你能用比较简捷的语言写出这一证明过程吗 与同伴交流.
情境导入
已知:如图,△ABC.
求证:∠A+∠B+∠C=180°.
分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
A
B
C
知识讲解
证明:作BC的延长线CD,过点C作射线CE∥AB,则
∠1=∠A(两直线平行,内错角相等),
∠2= ∠B(两直线平行,同位角相等).
又∵∠1+∠2+∠3= 180° (平角的定义),
∴∠A+∠B+∠ACB= 180° (等量代换).
你还有其他方法来证明三角形内角和定理吗
这里的CD,CE称为辅助线,辅助线通常画成虚线.
A
B
C
E
2
1
3
D
在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可行吗
请你帮小明把想法化为实际行动.
证明:过点A作PQ∥BC,则
∠1=∠B(两直线平行,内错角相等),
∠2=∠C(两直线平行,内错角相等),
又∵∠1+∠2+∠3= 180° (平角的定义),
∴ ∠BAC+∠B+∠C= 180° (等量代换).
小明的想法已经变为现实,由此你受到
什么启发 你有新的证法吗
A
B
C
P
Q
做一做
2
3
1
根据下面的图形,写出相应的证明.
你还能想出其他证法吗
(1)
A
B
C
P
Q
R
T
S
N
(3)
A
B
C
P
Q
R
M
T
S
N
(2)
A
B
C
P
Q
R
M
试一试
A
C
B
图1
B
A
C
图2
B A
C
图3
BAC
图4
先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另外两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果.
验证
C
B
A
如果BC不动,把点A“拉离”BC,
那么当点A越来越远离BC时,∠A就
越来越小(越来越接近0°),而
∠B和∠C则越来越大,它们的和
越来越接近180°, 当把点A拉
到无穷远时,便有AB∥AC,∠B和
∠C成为同旁内角,它们的和等于180°.由此你能想到什么
读一读
C
B
A
在△ABC中,如果BC不动,把点A“压”向BC,那么当点A越来越接近BC时, ∠A就越来越大(越来越接近180°),而∠B和∠C越来越小(越来越接近0°).由此你能想到什么
用橡皮筋构成△ABC,其中顶点B,C为定点,A为动点,放松橡皮筋后,点A自动收缩于BC上,请同学们考察点A变化时所形成的一系列的三角形,其内角会产生怎样的变化呢?
当点A远离BC时,∠A越来越趋近于0°,而AB与AC逐渐趋向平行,这时,∠B,∠C逐渐接近为互补的同旁内角,即∠B+∠C接近于180°.
试一试
结论
1.(昆明·中考)如图所示,
在△ABC中,CD是∠ACB的平分线,
∠A=80°,∠B=60°,
那么∠BDC=( )
A.80° B.90°
C.100° D.110°
练一练
2.(济宁·中考)若一个三角形三个内角度数的比为2∶3∶4,那么这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
【解析】选B.由题意可设这个三角形的三个内角度数分别
为2x,3x,4x,根据三角形内角和定理可得:2x+3x+4x=180°,
得x=20°,因此可得三个内角度数分别为40°,60°,80°.
3.(红河·中考) 如图,D,E分别是AB,AC上的点,若∠A=70°,∠B=60°,DE∥BC,则∠AED的度数是____.
【解析】因为∠A=70°,∠B=60°,所以∠C=50°,
又因为DE//BC,所以∠AED=∠C=50°.
答案:50°
4.(郴州·中考) 如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=___度.
【解析】如图,根据题意可知∠5=90°,
∴∠3+∠4=90°,
∴∠1+∠2=180°+180°-(∠3+∠4)
=360°-90°=270°.
答案:270
5. 如图,在△ABC中,∠A=60°,
∠B=70°,∠ACB的平分线交AB于D,
DE∥BC交AC于E,求∠EDC和∠BDC的
度数.
【解析】∵∠A=60°,∠B=70°,∴∠ACB=180°-60°
-70°=50°,∵CD是∠ACB的平分线,
∴∠ACD=∠BCD=25°,∵DE∥BC,∴∠EDC=∠BCD=25°.
在△BCD中,∠B=70°,∠BCD=25°,
∴∠BDC=180°-70°-25°=85°.
通过本课时的学习,需要我们掌握:
1.三角形的内角和是180°.
2.证明三角形内角和是180°,不仅可以通过实验操作验证,还可以通过严密的推理得到证明.通过平行线将三个内角拼在一起,得到一个平角或构造同旁内角是常用方法.
小结
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
