苏科版七年级数学下册第11章 一元一次不等式小结与思考 课件 (共21张PPT)
文档属性
| 名称 | 苏科版七年级数学下册第11章 一元一次不等式小结与思考 课件 (共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 180.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 11:31:16 | ||
图片预览








文档简介
(共21张PPT)
小结与思考
不等式
不等式的性质
1、不等式的两边都加上(或减去)
同一个数,所得不等式仍成立
2、不等式的两边都乘(或都除以)
同一个正数,所得不等式仍成立
不等式的两边都都乘(或都除以)
同一个负数,必须把不等号改变方向,
所得不等式仍成立
一元一次
不等式(组)
解一元一次不等式
解一元一次不等式组
在数轴上表示
不等式(组的
解集
知识结构图
一元一次不等式的应用
专题一
概念
一元一次不等式的定义:
1、含有一个未知数
2、未知数的最高次数为1
含有一个未知数,未知数的
次数是1的不等式,叫做
一元一次不等式.
一元一次不等式组的定义:
3、未知数的系数不为0
不等式的定义:
下列各式中,一元一次不等式有( )
(1)
(2)
(3)
(5)
(6)
(7)
(4)
A 5个 B 4个 C 6个 D 3个
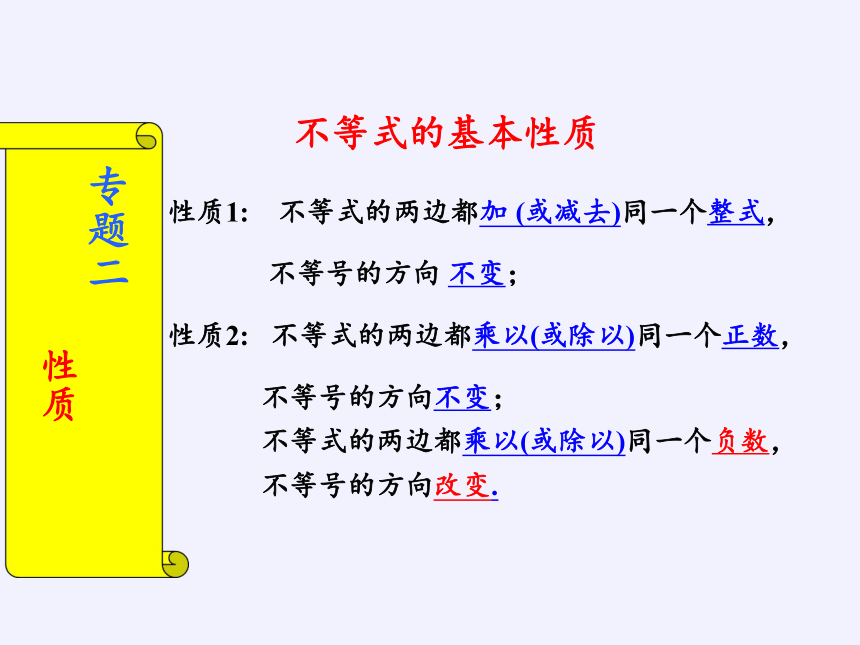
性质1: 不等式的两边都加 (或减去)同一个整式,
不等号的方向 不变;
性质2: 不等式的两边都乘以(或除以)同一个正数,
不等号的方向不变;
不等式的两边都乘以(或除以)同一个负数,
不等号的方向改变.
不等式的基本性质
专题二
性质
不等式的性质
<1> 若a>b, 则a+c>b+c
<2>若a>b, c>0 则ac>bc
若a>b, c<0, 则ac(1)若 的解集为 ,
求a的取值范围________。
(2)若不等式(a-2)x>a-2的解集为x<1,
求a的取值范围( )。
A a < -2 B a < 2 Ca >-2 D a >2
解下列不等式,并把解集表示在数轴上。
专题三
解一元一次不等式(组)
步骤 依据
去分母
不等式的性质2
去括号法则
不等式的性质1
合并同类项法则
不等式的性质2或3
归纳1、解一元一次不等式步骤及每一步变形的依据是什么?
系数化为1
合并同类项
移项
去括号
用数轴表示不等式的解集的步骤:
1.画数轴;
2.定界点;
3.定方向.
4.定虚实.
(1)求出不等式的最大整数解
最大整数解
(2)求出不等式的正整数解
(3)求出不等式的非负整数解
(4)不等式的整数解的个数?
(1)
(2)
解下列不等式组
(1)
(2)
同大取大
的解集是
当a>b时,
X>a
X>b
X>a
同小取小
的解集是
当a>b时,
X<a
X<b
X<b
大于小,小于大,在中间
的解集是
当a>b时,
X<a
X > b
b的解集是
当a>b时,
X > a
X < b
无解
文字记忆
数学语言
图形
归纳2、一元一次不等式组的解集及记忆方法
a
b
a
b
a
b
a
b
大于大,小于小,不存在
例1:已知不等式3x-a≤0的解是x≤3,求a的值
变式1:
不等式3x-a ≤ 0的正整数解为1,2,3,
变式2:
不等式3x-a<0的正整数解为1,2,3,求a的范围
变式3:
不等式3x-a≥0的负整数解为-1,-2,求a 的范围
例题讲解
求a的范围
数形结合思想
例2:不等式组 的解是
求 的值
不等式组
,求a的范围
变式一:
不等式组
无解,求a的范围
变式二:
有解
大显身手
数形结合思想
专题四
一元一次不等式的应用
娃哈哈饮料每瓶售价2元,现甲、乙两家商场给出优惠政策:甲商场全部9折,乙商场20瓶以上的部分8折。若你是消费者,选哪家商场购买比较合算?
如果关于x的方程3x+a=x+4的解是非负数,求a的取值范围。
X是非负数
不等式与方程结合的应用
总结归纳
本节课你收获了什么?
1、不等式、一元一次不等式(组)的定义
3、解一元一次不等式(组)
4、一元一次不等式的应用
5、数学思想的应用
2、不等式的基本性质
4、由不等式(m-5)x>m-5变形为x< 1,
则m需满足的条件是___________
2、若a >b,且a、b 、 c为有理数,则ac2___bc2
5、若y=-x+7,且2≤y≤7,则x的取值范围是_____
3、已知不等式 3(x+1) ≥5x-3 正整数解是_____
当堂反馈:
1、若a>b,则a-2___b-2,3a___3b,2-a___2-b
作业:
导学案055反面
谢 谢
小结与思考
不等式
不等式的性质
1、不等式的两边都加上(或减去)
同一个数,所得不等式仍成立
2、不等式的两边都乘(或都除以)
同一个正数,所得不等式仍成立
不等式的两边都都乘(或都除以)
同一个负数,必须把不等号改变方向,
所得不等式仍成立
一元一次
不等式(组)
解一元一次不等式
解一元一次不等式组
在数轴上表示
不等式(组的
解集
知识结构图
一元一次不等式的应用
专题一
概念
一元一次不等式的定义:
1、含有一个未知数
2、未知数的最高次数为1
含有一个未知数,未知数的
次数是1的不等式,叫做
一元一次不等式.
一元一次不等式组的定义:
3、未知数的系数不为0
不等式的定义:
下列各式中,一元一次不等式有( )
(1)
(2)
(3)
(5)
(6)
(7)
(4)
A 5个 B 4个 C 6个 D 3个
性质1: 不等式的两边都加 (或减去)同一个整式,
不等号的方向 不变;
性质2: 不等式的两边都乘以(或除以)同一个正数,
不等号的方向不变;
不等式的两边都乘以(或除以)同一个负数,
不等号的方向改变.
不等式的基本性质
专题二
性质
不等式的性质
<1> 若a>b, 则a+c>b+c
<2>若a>b, c>0 则ac>bc
若a>b, c<0, 则ac
求a的取值范围________。
(2)若不等式(a-2)x>a-2的解集为x<1,
求a的取值范围( )。
A a < -2 B a < 2 Ca >-2 D a >2
解下列不等式,并把解集表示在数轴上。
专题三
解一元一次不等式(组)
步骤 依据
去分母
不等式的性质2
去括号法则
不等式的性质1
合并同类项法则
不等式的性质2或3
归纳1、解一元一次不等式步骤及每一步变形的依据是什么?
系数化为1
合并同类项
移项
去括号
用数轴表示不等式的解集的步骤:
1.画数轴;
2.定界点;
3.定方向.
4.定虚实.
(1)求出不等式的最大整数解
最大整数解
(2)求出不等式的正整数解
(3)求出不等式的非负整数解
(4)不等式的整数解的个数?
(1)
(2)
解下列不等式组
(1)
(2)
同大取大
的解集是
当a>b时,
X>a
X>b
X>a
同小取小
的解集是
当a>b时,
X<a
X<b
X<b
大于小,小于大,在中间
的解集是
当a>b时,
X<a
X > b
b
当a>b时,
X > a
X < b
无解
文字记忆
数学语言
图形
归纳2、一元一次不等式组的解集及记忆方法
a
b
a
b
a
b
a
b
大于大,小于小,不存在
例1:已知不等式3x-a≤0的解是x≤3,求a的值
变式1:
不等式3x-a ≤ 0的正整数解为1,2,3,
变式2:
不等式3x-a<0的正整数解为1,2,3,求a的范围
变式3:
不等式3x-a≥0的负整数解为-1,-2,求a 的范围
例题讲解
求a的范围
数形结合思想
例2:不等式组 的解是
求 的值
不等式组
,求a的范围
变式一:
不等式组
无解,求a的范围
变式二:
有解
大显身手
数形结合思想
专题四
一元一次不等式的应用
娃哈哈饮料每瓶售价2元,现甲、乙两家商场给出优惠政策:甲商场全部9折,乙商场20瓶以上的部分8折。若你是消费者,选哪家商场购买比较合算?
如果关于x的方程3x+a=x+4的解是非负数,求a的取值范围。
X是非负数
不等式与方程结合的应用
总结归纳
本节课你收获了什么?
1、不等式、一元一次不等式(组)的定义
3、解一元一次不等式(组)
4、一元一次不等式的应用
5、数学思想的应用
2、不等式的基本性质
4、由不等式(m-5)x>m-5变形为x< 1,
则m需满足的条件是___________
2、若a >b,且a、b 、 c为有理数,则ac2___bc2
5、若y=-x+7,且2≤y≤7,则x的取值范围是_____
3、已知不等式 3(x+1) ≥5x-3 正整数解是_____
当堂反馈:
1、若a>b,则a-2___b-2,3a___3b,2-a___2-b
作业:
导学案055反面
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
