人教版七年级数学上册第一章 有理数《1.5.1乘方》教学设计
文档属性
| 名称 | 人教版七年级数学上册第一章 有理数《1.5.1乘方》教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 75.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 00:00:00 | ||
图片预览

文档简介
人教版七年级上册第一章 有理数
《1.5.1乘方》教学设计
一、教材分析
(一)教材的地位:本课时是在小学学过平方和立方、七上刚学习了有理数的乘法等计算以后的一个新知识点,即学生有一定的基础,但又是一个新内容。这一内容是后面即将学习的幂的乘方等内容的基础,所以学生要弄清弄懂“乘方”的概念,好为今后的学习打下良好的基础。
(二)教学目标:
1.知识与技能:
(1)理解有理数乘方的意义;
(2)正确理解乘方、幂、指数、底数等概念,会进行有理数乘方的运算;
(3)能熟练进行有理数的混合运算。
2.过程与方法:
(1)使学生能够灵活地进行乘方运算。
(2)通过对乘方意义的理解,培养学生观察、比较、分析、归纳、概括的能力,渗透转化的数学思想。
3.情感、态度和价质观
(1)通过对实例的感悟,让学生体会数学与生活的密切联系。
(2)学会数学的转化思想,培养学生灵活处理现实问题的能力。
(三)教学重点、难点
1.教学重点:正确理解乘方的意义,弄清底数、指数、幂等概念,掌握乘方运算法则。
2.教学难点:正确理解乘方的意义。
二、教法与学法
1、教法:引导探索,尝试指导,充分体现学生的主体地位。
2、学法:尝试探究、独立思考、合作与交流
三、教学过程
(一)创设情境,初探概念
问题组1:
1、边长为2cm的正方形的面积为 ;棱长为2cm的正方体的体积为 ;
2、把一张纸对折1次可得2层;把一张纸对折2次可得4层,即2×2层;
对折3次可得8层,即2×2×2层;
如果对折10次可得多少层?(请用一个算式表示,不用算出结果)
如果对折100次,算式中有几个2相乘?
师生活动:学生回答上面问题,教师引导:
如果2×2记作22;2×2×2记作23,那么(-2)×(-2)×(-2)应记作多少呢?呢?
设计意图:通过生活实例和问题情境,吸引学生的注意力,唤起学生的好奇心,激发学生兴趣和主动学习的欲望,营造一个让学生主动思考、探索的氛围。
(二)类比推理,归纳概念
问题组2:
上面这些式子都有什么共同特征?
你能用一般形式把它们表现出来吗?
这个式子实际上是对哪两种运算的一个转化?
为什么要进行这样的转化?
师生活动:学生充分交流的基础上,教师评议:1、都是乘法运算,2、因数相同。从而与学生共同得出概念.
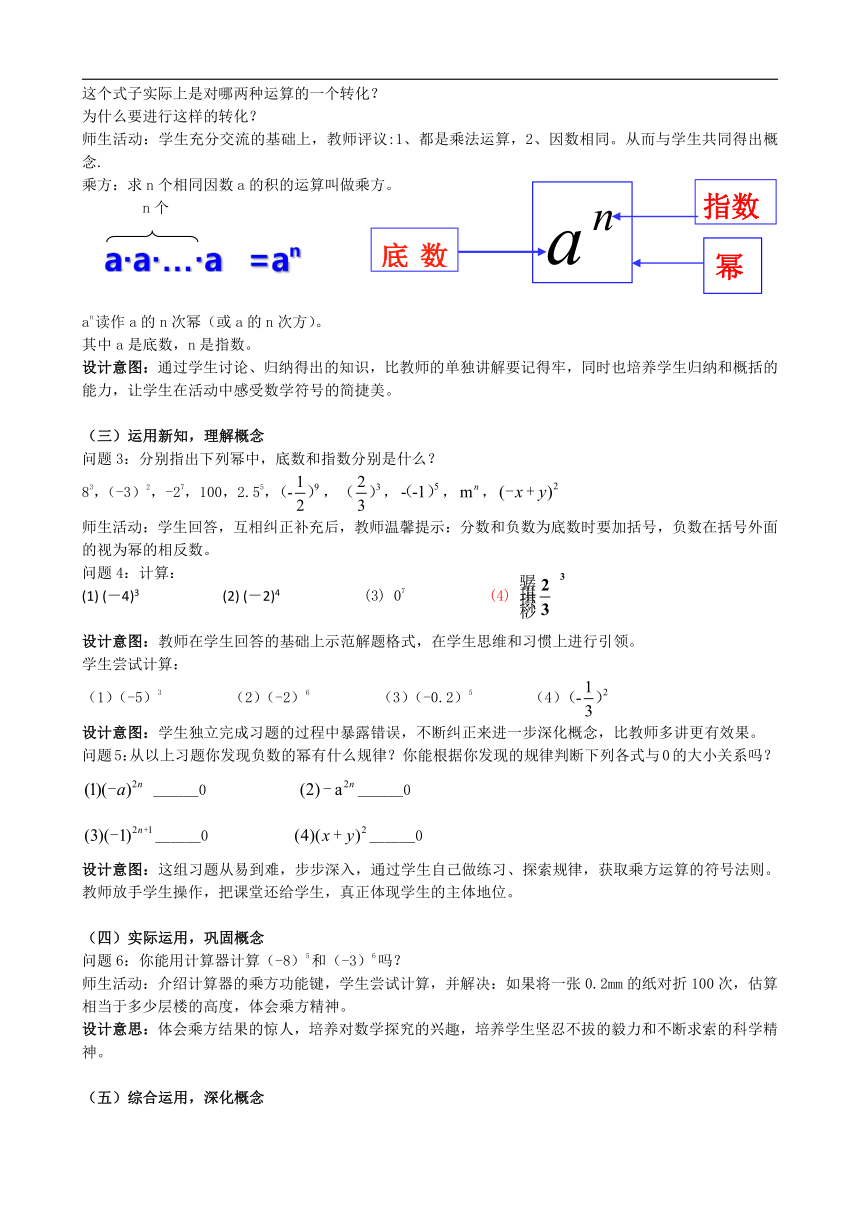
乘方:求n个相同因数a的积的运算叫做乘方。
n个
an读作a的n次幂(或a的n次方)。
其中a是底数,n是指数。
设计意图:通过学生讨论、归纳得出的知识,比教师的单独讲解要记得牢,同时也培养学生归纳和概括的能力,让学生在活动中感受数学符号的简捷美。
(三)运用新知,理解概念
问题3:分别指出下列幂中,底数和指数分别是什么?
83,(-3)2,-27,100,2.55,, ,,,
师生活动:学生回答,互相纠正补充后,教师温馨提示:分数和负数为底数时要加括号,负数在括号外面的视为幂的相反数。
问题4:计算:
(1) (-4)3 (2) (-2)4 (3) 07 (4)
设计意图:教师在学生回答的基础上示范解题格式,在学生思维和习惯上进行引领。
学生尝试计算:
(1)(-5)3 (2)(-2)6 (3)(-0.2)5 (4)
设计意图:学生独立完成习题的过程中暴露错误,不断纠正来进一步深化概念,比教师多讲更有效果。
问题5:从以上习题你发现负数的幂有什么规律?你能根据你发现的规律判断下列各式与0的大小关系吗?
___0 ___0
___0 ___0
设计意图:这组习题从易到难,步步深入,通过学生自己做练习、探索规律,获取乘方运算的符号法则。教师放手学生操作,把课堂还给学生,真正体现学生的主体地位。
(四)实际运用,巩固概念
问题6:你能用计算器计算(-8)5和(-3)6吗?
师生活动:介绍计算器的乘方功能键,学生尝试计算,并解决:如果将一张0.2mm的纸对折100次,估算相当于多少层楼的高度,体会乘方精神。
设计意思:体会乘方结果的惊人,培养对数学探究的兴趣,培养学生坚忍不拔的毅力和不断求索的科学精神。
(五)综合运用,深化概念
例2: 例3:
问题组7:
算式中含有哪些运算运算顺序应该是怎样的?
例2中你有其他方法解决吗?
设计意图:学生围绕问题独立思考并计算,小组内纠错并在全班交流练习经历:哪些地方喜欢出错,今后计算要注意哪些问题,把学生反馈、纠错培养成自觉行为,在提高计算能力的同时,让学生学会自我检查,自我反思。
问题8:观察下列三行数,你能回答下列问题?
-2,4,-8,16,-32,64,… ①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)取每行数的第10个数,计算这三个数的和.
设计意图:让学生在数列中巩固今天所学,把学数学转为用数学,体会学数学的乐趣。
(六)总结反思,升华提高
本节课你学到了什么?(知识?技能?思想方法等?)
1. 有理数的乘方的意义和相关概念。
2. 乘方的有关运算。
3. 体会化归的数学思想方法。
设计意图:让学生通过知识性内容的小结,把课堂教学传授的知识尽快转化为学生的素质;通过数学思想方法的小结,使学生更深刻地理解数学思想方法在解题中的地位和作用,逐步提高学生的归纳能力和语言表达能力。
附:课堂达标检测:
1、下列各式正确的是( )。
A.-12 = 1 B.- (-1)2 = 1 C.(-3)2 =-6 D.(-1)2n+1 = -1(n为正整数)
2、a为有理数,下列说法正确的是( )
A.(a+1)2的值总是正数 B.a2+1的值总是正数
C.(a-1)2的值总是正数 D.-a2+1的值总比1小
3、比较(-2)n和2 n的大小
4、计算:(1) (2)
四、板书设计:
数学方法: 数学思想: 例1: 课题
知识点:1、 2、 3、 a×a×a×……×a = an n个a
学生板演 例2: 例3: 学生板演
五、效果预测与反思
预测:本节课的教学设计是以新课程标准为依据,结合学生的实际情况,总体上采取教师创设问题———学生合作交流与自主探索———师生概括、评议、总结———学生练习、巩固、自查,四环节的教学思路,整个教学过程环环相扣,层层深入,以问题为线索,启发学生思考和探索,这样的设计符合学生的认知规律,使学生易于接受。学生在积极参与教师问题的探索和习题训练过程中,对于乘方的意义和概念的理解应该可以得到很好的突破和巩固,整个过程也可以培养学生探究问题,总结规律的能力,希望能让每位学生得到不同程度的知识提升和能力培养。
反思:
《1.5.1乘方》教学设计
一、教材分析
(一)教材的地位:本课时是在小学学过平方和立方、七上刚学习了有理数的乘法等计算以后的一个新知识点,即学生有一定的基础,但又是一个新内容。这一内容是后面即将学习的幂的乘方等内容的基础,所以学生要弄清弄懂“乘方”的概念,好为今后的学习打下良好的基础。
(二)教学目标:
1.知识与技能:
(1)理解有理数乘方的意义;
(2)正确理解乘方、幂、指数、底数等概念,会进行有理数乘方的运算;
(3)能熟练进行有理数的混合运算。
2.过程与方法:
(1)使学生能够灵活地进行乘方运算。
(2)通过对乘方意义的理解,培养学生观察、比较、分析、归纳、概括的能力,渗透转化的数学思想。
3.情感、态度和价质观
(1)通过对实例的感悟,让学生体会数学与生活的密切联系。
(2)学会数学的转化思想,培养学生灵活处理现实问题的能力。
(三)教学重点、难点
1.教学重点:正确理解乘方的意义,弄清底数、指数、幂等概念,掌握乘方运算法则。
2.教学难点:正确理解乘方的意义。
二、教法与学法
1、教法:引导探索,尝试指导,充分体现学生的主体地位。
2、学法:尝试探究、独立思考、合作与交流
三、教学过程
(一)创设情境,初探概念
问题组1:
1、边长为2cm的正方形的面积为 ;棱长为2cm的正方体的体积为 ;
2、把一张纸对折1次可得2层;把一张纸对折2次可得4层,即2×2层;
对折3次可得8层,即2×2×2层;
如果对折10次可得多少层?(请用一个算式表示,不用算出结果)
如果对折100次,算式中有几个2相乘?
师生活动:学生回答上面问题,教师引导:
如果2×2记作22;2×2×2记作23,那么(-2)×(-2)×(-2)应记作多少呢?呢?
设计意图:通过生活实例和问题情境,吸引学生的注意力,唤起学生的好奇心,激发学生兴趣和主动学习的欲望,营造一个让学生主动思考、探索的氛围。
(二)类比推理,归纳概念
问题组2:
上面这些式子都有什么共同特征?
你能用一般形式把它们表现出来吗?
这个式子实际上是对哪两种运算的一个转化?
为什么要进行这样的转化?
师生活动:学生充分交流的基础上,教师评议:1、都是乘法运算,2、因数相同。从而与学生共同得出概念.
乘方:求n个相同因数a的积的运算叫做乘方。
n个
an读作a的n次幂(或a的n次方)。
其中a是底数,n是指数。
设计意图:通过学生讨论、归纳得出的知识,比教师的单独讲解要记得牢,同时也培养学生归纳和概括的能力,让学生在活动中感受数学符号的简捷美。
(三)运用新知,理解概念
问题3:分别指出下列幂中,底数和指数分别是什么?
83,(-3)2,-27,100,2.55,, ,,,
师生活动:学生回答,互相纠正补充后,教师温馨提示:分数和负数为底数时要加括号,负数在括号外面的视为幂的相反数。
问题4:计算:
(1) (-4)3 (2) (-2)4 (3) 07 (4)
设计意图:教师在学生回答的基础上示范解题格式,在学生思维和习惯上进行引领。
学生尝试计算:
(1)(-5)3 (2)(-2)6 (3)(-0.2)5 (4)
设计意图:学生独立完成习题的过程中暴露错误,不断纠正来进一步深化概念,比教师多讲更有效果。
问题5:从以上习题你发现负数的幂有什么规律?你能根据你发现的规律判断下列各式与0的大小关系吗?
___0 ___0
___0 ___0
设计意图:这组习题从易到难,步步深入,通过学生自己做练习、探索规律,获取乘方运算的符号法则。教师放手学生操作,把课堂还给学生,真正体现学生的主体地位。
(四)实际运用,巩固概念
问题6:你能用计算器计算(-8)5和(-3)6吗?
师生活动:介绍计算器的乘方功能键,学生尝试计算,并解决:如果将一张0.2mm的纸对折100次,估算相当于多少层楼的高度,体会乘方精神。
设计意思:体会乘方结果的惊人,培养对数学探究的兴趣,培养学生坚忍不拔的毅力和不断求索的科学精神。
(五)综合运用,深化概念
例2: 例3:
问题组7:
算式中含有哪些运算运算顺序应该是怎样的?
例2中你有其他方法解决吗?
设计意图:学生围绕问题独立思考并计算,小组内纠错并在全班交流练习经历:哪些地方喜欢出错,今后计算要注意哪些问题,把学生反馈、纠错培养成自觉行为,在提高计算能力的同时,让学生学会自我检查,自我反思。
问题8:观察下列三行数,你能回答下列问题?
-2,4,-8,16,-32,64,… ①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)取每行数的第10个数,计算这三个数的和.
设计意图:让学生在数列中巩固今天所学,把学数学转为用数学,体会学数学的乐趣。
(六)总结反思,升华提高
本节课你学到了什么?(知识?技能?思想方法等?)
1. 有理数的乘方的意义和相关概念。
2. 乘方的有关运算。
3. 体会化归的数学思想方法。
设计意图:让学生通过知识性内容的小结,把课堂教学传授的知识尽快转化为学生的素质;通过数学思想方法的小结,使学生更深刻地理解数学思想方法在解题中的地位和作用,逐步提高学生的归纳能力和语言表达能力。
附:课堂达标检测:
1、下列各式正确的是( )。
A.-12 = 1 B.- (-1)2 = 1 C.(-3)2 =-6 D.(-1)2n+1 = -1(n为正整数)
2、a为有理数,下列说法正确的是( )
A.(a+1)2的值总是正数 B.a2+1的值总是正数
C.(a-1)2的值总是正数 D.-a2+1的值总比1小
3、比较(-2)n和2 n的大小
4、计算:(1) (2)
四、板书设计:
数学方法: 数学思想: 例1: 课题
知识点:1、 2、 3、 a×a×a×……×a = an n个a
学生板演 例2: 例3: 学生板演
五、效果预测与反思
预测:本节课的教学设计是以新课程标准为依据,结合学生的实际情况,总体上采取教师创设问题———学生合作交流与自主探索———师生概括、评议、总结———学生练习、巩固、自查,四环节的教学思路,整个教学过程环环相扣,层层深入,以问题为线索,启发学生思考和探索,这样的设计符合学生的认知规律,使学生易于接受。学生在积极参与教师问题的探索和习题训练过程中,对于乘方的意义和概念的理解应该可以得到很好的突破和巩固,整个过程也可以培养学生探究问题,总结规律的能力,希望能让每位学生得到不同程度的知识提升和能力培养。
反思:
