2021-2022学年数学苏科版七年级下册9.4乘法公式——完全平方公式同步训练(Word版 含答案)
文档属性
| 名称 | 2021-2022学年数学苏科版七年级下册9.4乘法公式——完全平方公式同步训练(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 109.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 00:00:00 | ||
图片预览



文档简介
9.4 乘法公式
一、单选题
1. 等于( )
A. B. C. D.
2.下列整式运算正确的是( )
A. (a﹣b)2=a2﹣b2 B. (a+2)(a﹣2)=a2﹣2
C. (a+2)(a﹣2)=a2﹣4 D.
3.若 , ,那么 值等于( )
A. 5200 B. 1484 C. 5804 D. 9904
4.如果 ,那么代数式 的值是( )
A. 2 B. 3 C. 5 D. 6
5、(﹣a﹣b)2等于( )
A.a2-2ab+b2 B.-a2+2ab﹣b2 C.a2+2ab+b2 D.-a2﹣2ab-b2
6、设,则( )
A.3 B. C.0 D.
7、若是完全平方式,则的值为( )
A.13 B. C.11或 D.或13.
8.下列计算中:①(2x)3·(-5x2y)=-10x5y;②(2a2-b)(2a2+b)=4a2-b2;③(x+3)(3-x)=x2-9;④(-x+y)(x+y)=-(x-y)(x+y)=-x2-y2 . 其中错误的有( )
A. 1个 B. 2个 C. 3个 D. 4个
9.为了应用平方差公式计算(a﹣b+c)(a+b﹣c),必须先适当变形,下列变形中,正确的是( )
A. [(a+c)﹣b] [(a﹣c)+b] B. [(a﹣b)+c][(a+b)﹣c]
C. [a﹣(b+c)] [a+(b﹣c)] D. [a﹣(b﹣c)] [a+(b﹣c)]
10.计算(x4+1)(x2+1)(x+1)(x﹣1)的结果是( )
A. x +1 B. x ﹣1 C. (x+1) D. (x﹣1)
二、填空题
11.计算:20202﹣4040×2019+20192=________.
12.如果是完全平方式,则的值是___________________.
13.计算:______________.
14.已知,,则__________.
15.我围古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)“的展开式的各项系数,此三角形称为“杨辉三角”.
根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为________.
三、解答题
16.计算
(1)
(2)(﹣a)2 a4÷a3
(3)(2x﹣1)(x﹣3)
(4)(3x﹣2y)2(3x+2y)2
(5)(x﹣2y+4)(x﹣2y﹣4)
17课堂上,老师让同学们计算 ,左边文本框中是小方的解题过程.请你作为小老师对其进行评价,判断其是否正确?如果有错误,请写出正确的解题过程.
21.某同学化简a(a+2b)﹣(a+b)(a﹣b)出现了不正确,解答过程如下:
原式=a2+2ab﹣(a2﹣b2) (第一步)
=a2+2ab﹣a2﹣b2(第二步)
=2ab﹣b2 (第三步)
(1)该同学解答过程从第________步开始出错,不正确原因是________;
(2)写出此题正确的解答过程.
18.观察下列等式: (x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(x﹣1)(x4+x3+x2+x+1)=x5﹣1…
运用上述规律,试求26+25+24+23+22+2+1的值.
19 .(1)当 , 时,分别求代数式 和 的值;
(2)当 , 时, ________ (填“ ”,“ ”,“ ”)
(3)观察(1)(2)中代探索代数式 和 有何数量关系,并把探索的结果写出来: ________ (填“ ”,“ ”,“ ”)
(4)利用你发现的规律,求 的值.
20.如图1,A纸片是边长为a的正方形,B纸片是边长为b的正方形,C纸片是长为b,宽为a的长方形.现用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积.
方法1:________;方法2:________;
(2)观察图2,请你写出下列三个代数式:(a+b)2 , a2+b2 , ab之间的等量关系________;
(3)根据(2)题中的等量关系,解决如下问题:若a+b=5,a2+b2=13,求ab的值;
21(阅读理解)“若 满足 ,求 的值”.
解:设 , ,则 ,
,
(解决问题)
(1)若 满足 ,则 的值为________;
(2)若满足 ,则 的值为________;
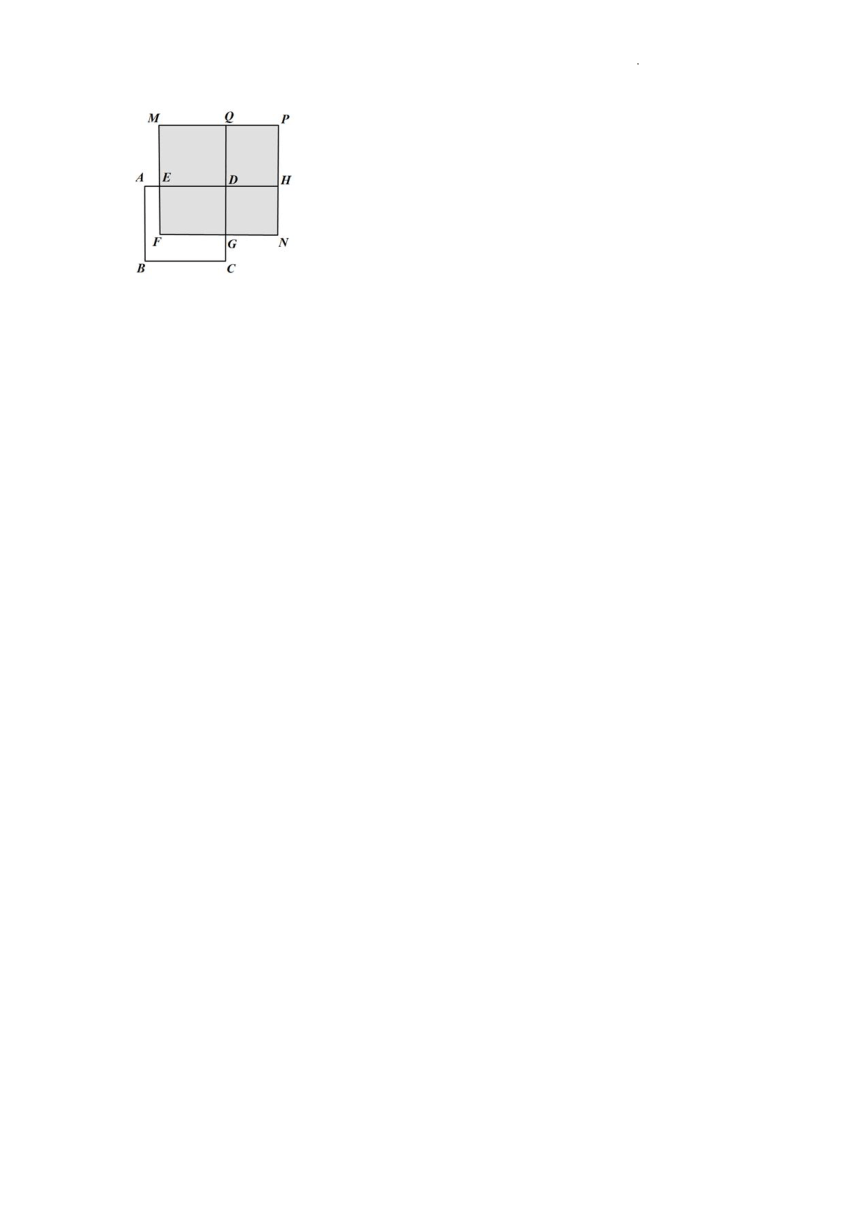
(3)如图,正方形 的边长为 , , ,长方形 的面积是200,四边形 和 都是正方形,四边形 是长方形,求图中阴影部分的面积(结果必须是一个具体的数值).
1.B2.C 3.D 4.C 5.C 6.D 7.D 8.D9.D 10.B
11. 1
12.
13.250000
14.29.
15.190
16. 解:(1)
=﹣4﹣2+1
=﹣5;
(2)(﹣a)2 a4÷a3
=a2 a4÷a3
=a3;
(3)(2x﹣1)(x﹣3)
=2x2﹣6x﹣x+3
=2x2﹣7x+3;
(4)(3x﹣2y)2(3x+2y)2
=[(3x﹣2y)(3x+2y)]2
=(9x2﹣4y2)2
=81x4﹣72x2y2+16y4
(5)(x﹣2y+4)(x﹣2y﹣4)
=(x﹣2y)2﹣42
=x2﹣4xy+4y2﹣16
【考点】完全平方公式及运用,平方差公式及应用,0指数幂的运算性质
【分析】(1)根据有理数的乘方法则、负整数指数幂的定义和零指数幂的定义计算,再合并即可;
(2)根据同底数幂的乘除法法则计算即可;
(3)根据多项式与多项式相乘的法则计算,再合并即可;
(4)先运用平方差公式计算,再运用完全平方公式计算即可;
(5)先运用平方差公式计算,再运用完全平方公式计算即可.
17【答案】解:小方的解题过程不正确.
正确的解答:原式=
【考点】单项式乘多项式,平方差公式
【分析】先利用平方差公式计算,再利用单项式乘以多项式法则去括号,合并同类项即可.
18【答案】 (1)二;去括号时没有变号
(2)解:原式=a2+2ab﹣(a2﹣b2)
=a2+2ab﹣a2+b2
=2ab+b2 .
【考点】平方差公式及应用,整式的混合运算
解:(1)该同学解答过程从第 二步开始出错,不正确原因是去括号时没有变号;
故答案为:二,去括号时没有变号;
【分析】(1)逐步分析查找不符合运算法则的步骤即可.(2)先计算乘法,然后计算减法.
18.【答案】解:设26+25+…+2+1=S, 则(2﹣1)S=(2﹣1)(26+25+…+2+1)=27﹣1,
∴S=27﹣1.
【考点】平方差公式
【分析】设26+25+…+2+1=S,两边都乘以(2﹣1),根据已知式子得出的规律求出即可.
19.【答案】 (1)解:当 , 时,
,
.
(2)=
(3)=
(4)解:
【考点】完全平方公式及运用
解:(2)当 , 时,
,
;
;
故答案为:=;
(3)前两个小题计算结果经验证,可得: ;
故答案为:=;
【分析】(1)将a、b的值代入代数式计算即可求解;
(2)将a、b的值代入代数式计算,并比较计算结果即可判断求解;
(3)观察(1)和(2)的结果可判断求解;
(4)由(3)可知,把135.7看作a,35.7看作b,代入公式(a-b)2计算即可求解.
20.【答案】 (1)(a+b)2;a2+b2+2ab
(2)(a+b)2=a2+b2+2ab
(3)解:因为a+b=5,a2+b2=13,
所以52=13+2ab,所以ab=6.
【考点】完全平方公式及运用,完全平方公式的几何背景
解:(1)方法1:图2大正方形的面积=(a+b)2 , 图2大正方形的面积= a2+b2+2ab;
故答案为:(a+b)2 , a2+b2+2ab;
( 2 )根据同一图形的面积相等可得:(a+b)2= a2+b2+2ab;
故答案为:(a+b)2= a2+b2+2ab;
【分析】(1)正方形的面积可以直接求,也可以是四个图形面积的和,据此解答即可;
(2)根据同一图形的面积相等即得答案;
(3)将已知的式子代入(2)题中的等式计算即可.
21.【答案】 (1)140
(2)10
(3)解:由题意得: , ,∴ ,设 , ,
则 , ,
∵四边形 和 都是正方形,∴ , ,
∴ .
【考点】完全平方公式及运用,完全平方公式的几何背景
解:(1)设 , ,
则 , ,
∴ =a2+b2 ;
故答案为:140;
( 2 )设 , ,
则 , ,
∴ ;
故答案为:10;
【分析】(1)根据阅读理解中提供的思路和方法解答即可;
(2)设 , ,求出ab和﹣a+2b的值后再根据阅读理解中提供的方法求解即可;(3)由题意可得: ,设 , ,易得ab与a-b的值,然后根据 解答即可.
一、单选题
1. 等于( )
A. B. C. D.
2.下列整式运算正确的是( )
A. (a﹣b)2=a2﹣b2 B. (a+2)(a﹣2)=a2﹣2
C. (a+2)(a﹣2)=a2﹣4 D.
3.若 , ,那么 值等于( )
A. 5200 B. 1484 C. 5804 D. 9904
4.如果 ,那么代数式 的值是( )
A. 2 B. 3 C. 5 D. 6
5、(﹣a﹣b)2等于( )
A.a2-2ab+b2 B.-a2+2ab﹣b2 C.a2+2ab+b2 D.-a2﹣2ab-b2
6、设,则( )
A.3 B. C.0 D.
7、若是完全平方式,则的值为( )
A.13 B. C.11或 D.或13.
8.下列计算中:①(2x)3·(-5x2y)=-10x5y;②(2a2-b)(2a2+b)=4a2-b2;③(x+3)(3-x)=x2-9;④(-x+y)(x+y)=-(x-y)(x+y)=-x2-y2 . 其中错误的有( )
A. 1个 B. 2个 C. 3个 D. 4个
9.为了应用平方差公式计算(a﹣b+c)(a+b﹣c),必须先适当变形,下列变形中,正确的是( )
A. [(a+c)﹣b] [(a﹣c)+b] B. [(a﹣b)+c][(a+b)﹣c]
C. [a﹣(b+c)] [a+(b﹣c)] D. [a﹣(b﹣c)] [a+(b﹣c)]
10.计算(x4+1)(x2+1)(x+1)(x﹣1)的结果是( )
A. x +1 B. x ﹣1 C. (x+1) D. (x﹣1)
二、填空题
11.计算:20202﹣4040×2019+20192=________.
12.如果是完全平方式,则的值是___________________.
13.计算:______________.
14.已知,,则__________.
15.我围古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)“的展开式的各项系数,此三角形称为“杨辉三角”.
根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为________.
三、解答题
16.计算
(1)
(2)(﹣a)2 a4÷a3
(3)(2x﹣1)(x﹣3)
(4)(3x﹣2y)2(3x+2y)2
(5)(x﹣2y+4)(x﹣2y﹣4)
17课堂上,老师让同学们计算 ,左边文本框中是小方的解题过程.请你作为小老师对其进行评价,判断其是否正确?如果有错误,请写出正确的解题过程.
21.某同学化简a(a+2b)﹣(a+b)(a﹣b)出现了不正确,解答过程如下:
原式=a2+2ab﹣(a2﹣b2) (第一步)
=a2+2ab﹣a2﹣b2(第二步)
=2ab﹣b2 (第三步)
(1)该同学解答过程从第________步开始出错,不正确原因是________;
(2)写出此题正确的解答过程.
18.观察下列等式: (x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(x﹣1)(x4+x3+x2+x+1)=x5﹣1…
运用上述规律,试求26+25+24+23+22+2+1的值.
19 .(1)当 , 时,分别求代数式 和 的值;
(2)当 , 时, ________ (填“ ”,“ ”,“ ”)
(3)观察(1)(2)中代探索代数式 和 有何数量关系,并把探索的结果写出来: ________ (填“ ”,“ ”,“ ”)
(4)利用你发现的规律,求 的值.
20.如图1,A纸片是边长为a的正方形,B纸片是边长为b的正方形,C纸片是长为b,宽为a的长方形.现用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积.
方法1:________;方法2:________;
(2)观察图2,请你写出下列三个代数式:(a+b)2 , a2+b2 , ab之间的等量关系________;
(3)根据(2)题中的等量关系,解决如下问题:若a+b=5,a2+b2=13,求ab的值;
21(阅读理解)“若 满足 ,求 的值”.
解:设 , ,则 ,
,
(解决问题)
(1)若 满足 ,则 的值为________;
(2)若满足 ,则 的值为________;
(3)如图,正方形 的边长为 , , ,长方形 的面积是200,四边形 和 都是正方形,四边形 是长方形,求图中阴影部分的面积(结果必须是一个具体的数值).
1.B2.C 3.D 4.C 5.C 6.D 7.D 8.D9.D 10.B
11. 1
12.
13.250000
14.29.
15.190
16. 解:(1)
=﹣4﹣2+1
=﹣5;
(2)(﹣a)2 a4÷a3
=a2 a4÷a3
=a3;
(3)(2x﹣1)(x﹣3)
=2x2﹣6x﹣x+3
=2x2﹣7x+3;
(4)(3x﹣2y)2(3x+2y)2
=[(3x﹣2y)(3x+2y)]2
=(9x2﹣4y2)2
=81x4﹣72x2y2+16y4
(5)(x﹣2y+4)(x﹣2y﹣4)
=(x﹣2y)2﹣42
=x2﹣4xy+4y2﹣16
【考点】完全平方公式及运用,平方差公式及应用,0指数幂的运算性质
【分析】(1)根据有理数的乘方法则、负整数指数幂的定义和零指数幂的定义计算,再合并即可;
(2)根据同底数幂的乘除法法则计算即可;
(3)根据多项式与多项式相乘的法则计算,再合并即可;
(4)先运用平方差公式计算,再运用完全平方公式计算即可;
(5)先运用平方差公式计算,再运用完全平方公式计算即可.
17【答案】解:小方的解题过程不正确.
正确的解答:原式=
【考点】单项式乘多项式,平方差公式
【分析】先利用平方差公式计算,再利用单项式乘以多项式法则去括号,合并同类项即可.
18【答案】 (1)二;去括号时没有变号
(2)解:原式=a2+2ab﹣(a2﹣b2)
=a2+2ab﹣a2+b2
=2ab+b2 .
【考点】平方差公式及应用,整式的混合运算
解:(1)该同学解答过程从第 二步开始出错,不正确原因是去括号时没有变号;
故答案为:二,去括号时没有变号;
【分析】(1)逐步分析查找不符合运算法则的步骤即可.(2)先计算乘法,然后计算减法.
18.【答案】解:设26+25+…+2+1=S, 则(2﹣1)S=(2﹣1)(26+25+…+2+1)=27﹣1,
∴S=27﹣1.
【考点】平方差公式
【分析】设26+25+…+2+1=S,两边都乘以(2﹣1),根据已知式子得出的规律求出即可.
19.【答案】 (1)解:当 , 时,
,
.
(2)=
(3)=
(4)解:
【考点】完全平方公式及运用
解:(2)当 , 时,
,
;
;
故答案为:=;
(3)前两个小题计算结果经验证,可得: ;
故答案为:=;
【分析】(1)将a、b的值代入代数式计算即可求解;
(2)将a、b的值代入代数式计算,并比较计算结果即可判断求解;
(3)观察(1)和(2)的结果可判断求解;
(4)由(3)可知,把135.7看作a,35.7看作b,代入公式(a-b)2计算即可求解.
20.【答案】 (1)(a+b)2;a2+b2+2ab
(2)(a+b)2=a2+b2+2ab
(3)解:因为a+b=5,a2+b2=13,
所以52=13+2ab,所以ab=6.
【考点】完全平方公式及运用,完全平方公式的几何背景
解:(1)方法1:图2大正方形的面积=(a+b)2 , 图2大正方形的面积= a2+b2+2ab;
故答案为:(a+b)2 , a2+b2+2ab;
( 2 )根据同一图形的面积相等可得:(a+b)2= a2+b2+2ab;
故答案为:(a+b)2= a2+b2+2ab;
【分析】(1)正方形的面积可以直接求,也可以是四个图形面积的和,据此解答即可;
(2)根据同一图形的面积相等即得答案;
(3)将已知的式子代入(2)题中的等式计算即可.
21.【答案】 (1)140
(2)10
(3)解:由题意得: , ,∴ ,设 , ,
则 , ,
∵四边形 和 都是正方形,∴ , ,
∴ .
【考点】完全平方公式及运用,完全平方公式的几何背景
解:(1)设 , ,
则 , ,
∴ =a2+b2 ;
故答案为:140;
( 2 )设 , ,
则 , ,
∴ ;
故答案为:10;
【分析】(1)根据阅读理解中提供的思路和方法解答即可;
(2)设 , ,求出ab和﹣a+2b的值后再根据阅读理解中提供的方法求解即可;(3)由题意可得: ,设 , ,易得ab与a-b的值,然后根据 解答即可.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
