2021-2022学年苏科版七年级数学下册7~8章阶段练(4)(培优)(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册7~8章阶段练(4)(培优)(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 992.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 23:12:10 | ||
图片预览



文档简介
7~8章 阶段练(4)(培优)【平面图形的认识(二)、幂的运算】
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、下列是四个汽车标志图案,其中可看作由“基本图案”经过平移得到的是( )
A. B. C. D.
2、(2020南通期末)若,则n=( )
A.2022 B.2021 C.2020 D.2019
3、(2020·淮阳市七年级期末)计算的结果为( )
A. B. C. D.2
4、(2020·山东德州市·八年级期末)已知,则的值是( )
A.48 B.16 C.12 D.8
5、(2021春 济阳区期末)如果a=(﹣99)0,b=(﹣0.1)﹣1,c=,那么a、b、c的大小关系为( )
A.a>b>c B.c>a>b C.a>c>b D.c>b>a
6、如图,△EFG 的三个顶点 E,G 和 F 分别在平行线 AB,CD 上,FH 平分∠EFG,交线段 EG 于 点 H,若∠AEF=36°,∠BEG=57°,则∠EHF 的大小为( )
A.105° B.75° C.90° D.95°
(6题) (7题) (8题)
7、(2020春 天宁区校级期中)如图,将长方形ABCD沿直线EF折叠到ED 'C 'F的位置,若∠DEF=70°,则∠BFC '的度数为( )
A.20° B.30° C.40° D.50°
8、(2020春 仪征市期中)如图在五边形ABCDE中,∠A=∠B=∠C=∠D,∠DEF=3∠AEF,则∠AFE度数是( )
A.45° B.60° C.72° D.无法确定
9、(2020春 常州期中)如图,将△ABC纸片沿DE折叠,点A的对应点为A’,若∠B=60°,∠C=80°,则∠1+∠2等于( )
A.40° B.60° C.80° D.140°
(9题) (10题)
10、(2020春 泰兴市校级期中)如图,在△ABC中,∠A=48°,∠ABC与∠ACD的平分线交于点,得∠;∠BC与∠CD的平分线相交于点,得∠;……;∠BC与∠CD的平分线交于点,要使∠的度数为整数,则n的最大值为( )
A.2 B.3 C.4 D.5
二、填空题
11、(2020·江西南昌市·七年级期中)计算的结果是_________.
12、(2020常州期末)已知2x﹣6y+6=0,则2x÷8y=_____.
13、若(am+1bn+2)(a2n﹣1b2n)=a5b3,则求m+n的值=__________.
14、若ma=2,mb=3,mc=4,则m2a+b﹣c= .
15、(2020春 玄武区期中)233、418、810的大小关系是(用>号连接) .
16、将一副直角三角板如图摆放,点A落在边上,,则______.
(16题) (17题)
17、(2020春 高新区期中)如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD= .
18、阅读材料:①1的任何次幂都等于1;②﹣1的奇数次幂都等于﹣1;③﹣1的偶数次幂都等于1;
④任何不等于零的数的零次幂都等于1,
试根据以上材料探索使等式(2x+3)x+2016=1成立的x的值为 .
三、解答题
19、(2019春 漳浦县期中)计算
(1)(m﹣n)2 (n﹣m)3 (n﹣m)4 (2)(b2n)3(b3)4n÷(b5)n+1
(3)(a2)3﹣a3 a3+(2a3)2; (4)(﹣4am+1)3÷[2(2am)2 a].
20、(2021春 仪征市期中)(1)已知10m=5,10n=2,求103m+2n的值;
(2)已知8m÷4n=16,求(﹣3)2n﹣3m的值.
21、(2020苏州七年级期中)已知:如图,,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:;
(2)若∠BFE=110°,∠A=60°,求∠B的度数.
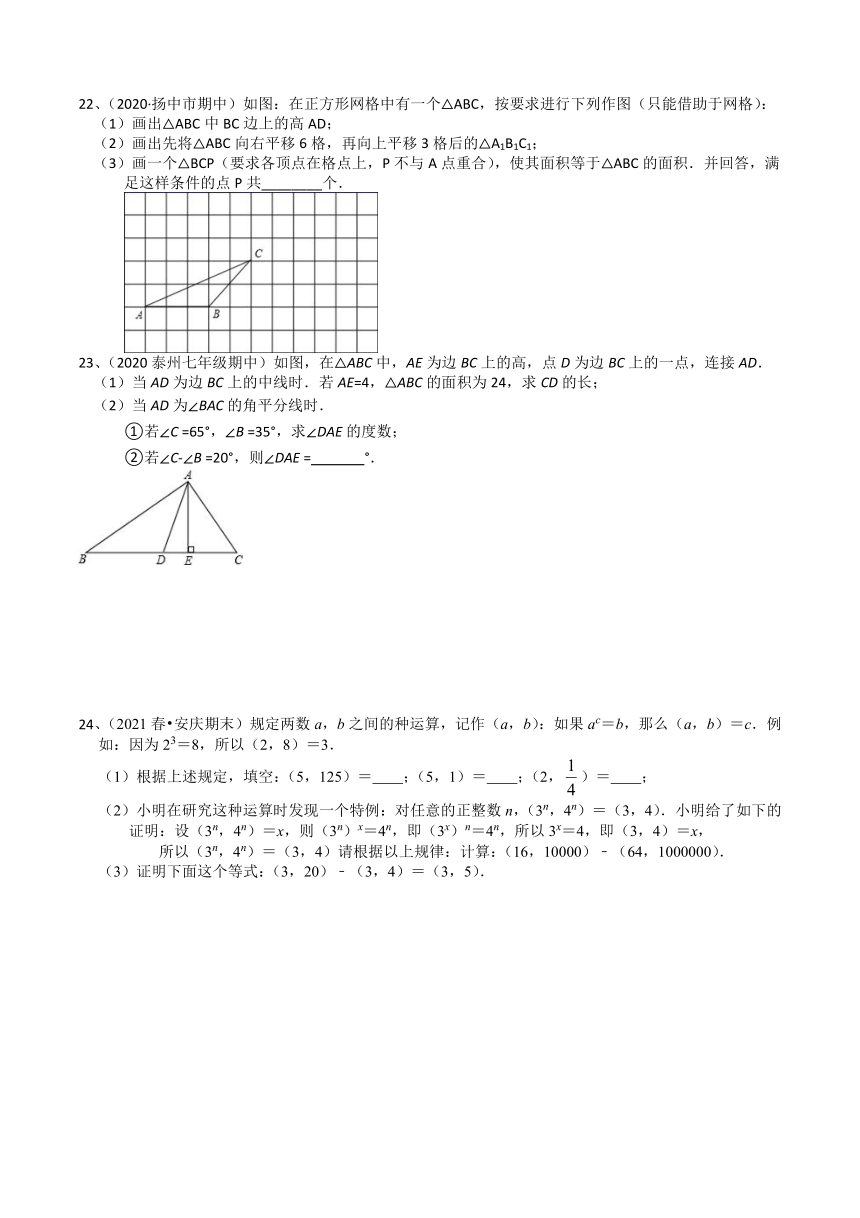
22、(2020·扬中市期中)如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)画一个△BCP(要求各顶点在格点上,P不与A点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共________个.
23、(2020泰州七年级期中)如图,在△ABC中,AE为边BC上的高,点D为边BC上的一点,连接AD.
(1)当AD为边BC上的中线时.若AE=4,△ABC的面积为24,求CD的长;
(2)当AD为∠BAC的角平分线时.
①若∠C =65°,∠B =35°,求∠DAE的度数;
②若∠C-∠B =20°,则∠DAE = °.
24、(2021春 安庆期末)规定两数a,b之间的种运算,记作(a,b):如果ac=b,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:(5,125)= ;(5,1)= ;(2,)= ;
(2)小明在研究这种运算时发现一个特例:对任意的正整数n,(3n,4n)=(3,4).小明给了如下的 证明:设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n,所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4)请根据以上规律:计算:(16,10000)﹣(64,1000000).
(3)证明下面这个等式:(3,20)﹣(3,4)=(3,5).
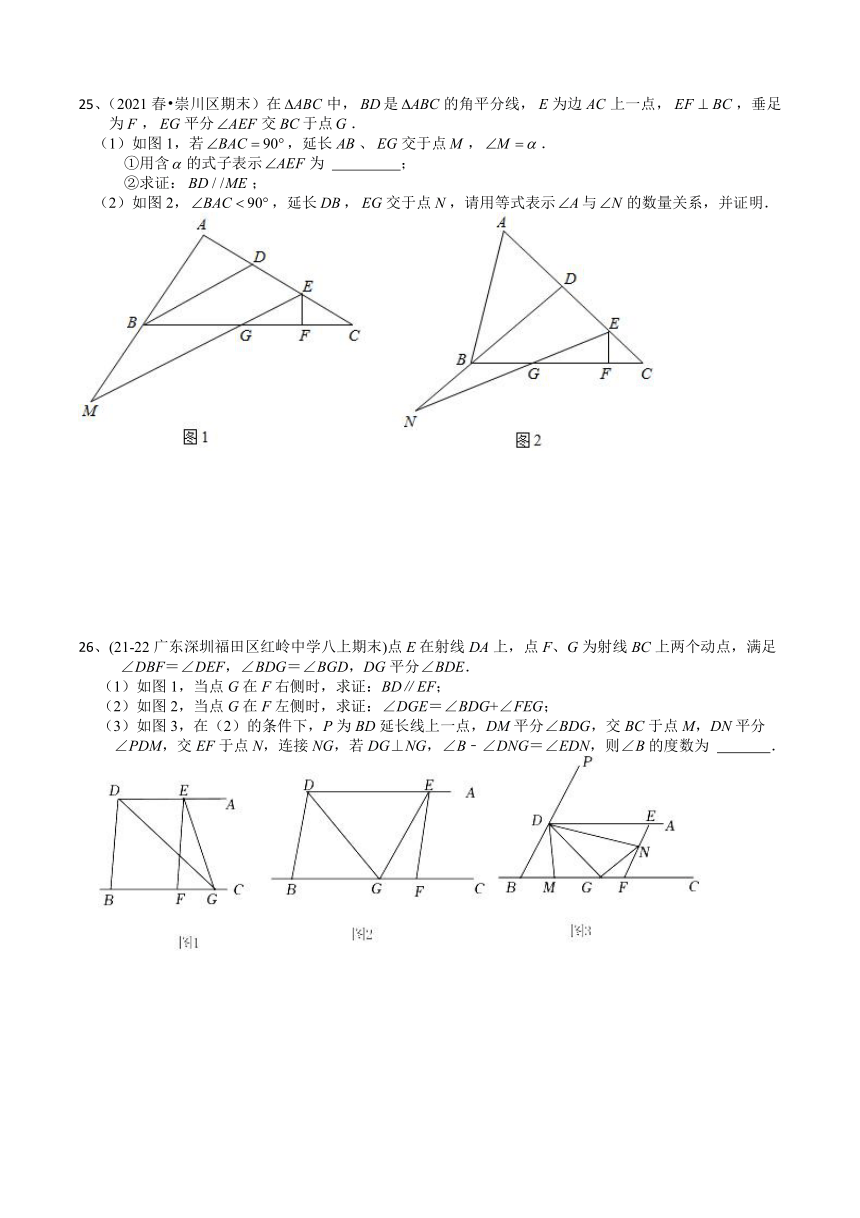
25、(2021春 崇川区期末)在中,是的角平分线,为边上一点,,垂足为,平分交于点.
(1)如图1,若,延长、交于点,.
①用含的式子表示为 ;
②求证:;
(2)如图2,,延长,交于点,请用等式表示与的数量关系,并证明.
26、(21-22广东深圳福田区红岭中学八上期末)点E在射线DA上,点F、G为射线BC上两个动点,满足
∠DBF=∠DEF,∠BDG=∠BGD,DG平分∠BDE.
(1)如图1,当点G在F右侧时,求证:BD∥EF;
(2)如图2,当点G在F左侧时,求证:∠DGE=∠BDG+∠FEG;
(3)如图3,在(2)的条件下,P为BD延长线上一点,DM平分∠BDG,交BC于点M,DN平分
∠PDM,交EF于点N,连接NG,若DG⊥NG,∠B﹣∠DNG=∠EDN,则∠B的度数为 .
7~8章 阶段练(4)(培优)【平面图形的认识(二)、幂的运算】
-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、下列是四个汽车标志图案,其中可看作由“基本图案”经过平移得到的是( )
A. B. C. D.
【答案】B
【分析】
根据平移的概念观察即可
【详解】
解:由“基本图案”经过旋转得到
由“基本图案”经过平移得到
由“基本图案”经过翻折得到
不能由 “基本图案”经过平移得到
故选:B
2、(2020南通期末)若,则n=( )
A.2022 B.2021 C.2020 D.2019
【答案】A
【分析】本题考查了乘方的意义,以及同底数幂的乘法运算.注意:求n个相同因数乘积的运算,叫做乘方,乘方的结果叫做幂.
2020个2020相乘,可以写成,2020个2020相加,可以写成,计算即可得到答案.
【详解】∵,
,
∴原式左边,
即,∴.
故选:A.
3、(2020·淮阳市七年级期末)计算的结果为( )
A. B. C. D.2
【答案】B
【分析】本题考查了有理数的混合运算,解题的关键是合理利用同底数幂的乘法法则进行简便运算.
根据同底数幂的乘法法则运算即可.
【详解】
解:
=
=
=
=
故选B.
4、(2020·山东德州市·八年级期末)已知,则的值是( )
A.48 B.16 C.12 D.8
【答案】A
【分析】本题是对同底数幂乘除的考查,熟练掌握整式的乘除是解决本题的关键.
先把化成,再计算即可.
【详解】先把化成,
原式===48,
故选A.
5、(2021春 济阳区期末)如果a=(﹣99)0,b=(﹣0.1)﹣1,c=,那么a、b、c的大小关系为( )
A.a>b>c B.c>a>b C.a>c>b D.c>b>a
【分析】根据负整数指数次幂等于正整数指数次幂的倒数,任何非零数的零指数次幂等于1求出a、b、c,然后按照从大到小的顺序排列即可.
【解答】解:a=(﹣99)0=1,
b=(﹣0.1)﹣1=﹣10,
c=()﹣2=9,
所以c>a>b.
故选:B.
6、如图,△EFG 的三个顶点 E,G 和 F 分别在平行线 AB,CD 上,FH 平分∠EFG,交线段 EG 于 点 H,若∠AEF=36°,∠BEG=57°,则∠EHF 的大小为( )
A.105° B.75° C.90° D.95°
【答案】B
【分析】
首先根据∠AEF=36°,∠BEG=57°,求出∠FEH的大小;然后根据AB∥CD,求出∠EFG的大小,再根据FH平分∠EFG,求出∠EFH的大小;最后根据三角形内角和定理,求出∠EHF的大小为多少即可.
【详解】
解:∵∠AEF=36°,∠BEG=57°,∴∠FEH=180°-36°-57°=87°;
∵AB∥CD,∴∠EFG=∠AEF=36°,
∵FH平分∠EFG,∴∠EFH=∠EFG=×36°=18°,
∴∠EHF=180°-∠FEH-∠EFH=180°-87°-18°=75°.
故选:B.
7、(2020春 天宁区校级期中)如图,将长方形ABCD沿直线EF折叠到ED 'C 'F的位置,若∠DEF=70°,则∠BFC '的度数为( )
A.20° B.30° C.40° D.50°
解:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠DEF=∠EFB(两直线平行,内错角相等),
∵∠DEF=70°,
∴∠EFB=70°,
∵长方形ABCD沿直线EF折叠到ED'C'F的位置,
∴ED′∥FC′,∠D′EF=∠DEF=70°,
∴∠D′EF+∠C′FE=180°(两直线平行,同旁内角互补),
∴∠C′FE=110°,
∴∠BFC'=∠C′FE﹣∠EFB=110°﹣70°=40°,
故选:C.
8、(2020春 仪征市期中)如图在五边形ABCDE中,∠A=∠B=∠C=∠D,∠DEF=3∠AEF,则∠AFE度数是( )
A.45° B.60° C.72° D.无法确定
解:设∠A=∠B=∠C=∠D=x°,∠AEF=y°,则∠DEF=3y°,依题意有
4x+4y=540,
解得x+y=135,
则∠AFE=180°﹣135°=45°.
故选:A.
9、(2020春 常州期中)如图,将△ABC纸片沿DE折叠,点A的对应点为A’,若∠B=60°,∠C=80°,则∠1+∠2等于( )
A.40° B.60° C.80° D.140°
解:连接AA′.
∵∠B=60°,∠C=80°,
∴∠A=40°
∵∠2=∠EA′A+∠EAA′,∠1=∠DA′A+∠DAA′,∠BAC=∠EA′D,
∴∠1+∠2=∠EA′A+∠EAA′+∠DA′A+∠DAA′=∠EAD+∠EA′D=2∠EAD=80°,
故选:C.
10、(2020春 泰兴市校级期中)如图,在△ABC中,∠A=48°,∠ABC与∠ACD的平分线交于点,得∠;∠BC与∠CD的平分线相交于点,得∠;……;∠BC与∠CD的平分线交于点,要使∠的度数为整数,则n的最大值为( )
A.2 B.3 C.4 D.5
解:∵∠ABC与∠ACD的平分线交于点A1,
∴∠A1=180°﹣∠ACD﹣∠ACB﹣∠ABC
=180°﹣(∠ABC+∠A)﹣(180°﹣∠A﹣∠ABC)﹣∠ABC
=∠A
=;
同理可得∠A2=∠A1=,…
∴∠An=.
∴要使∠An的度数为整数,则n的最大值为4,此时∠A4=3°.
故选:C.
二、填空题
11、(2020·江西南昌市·七年级期中)计算的结果是_________.
【答案】
【分析】本题主要考查幂的运算法则,熟练掌握幂的运算法则是解答本题的关键.
先用同底数幂乘法逆运算将变为,再提公因数计算即可.
【详解】,
故答案为:
12、(2020常州期末)已知2x﹣6y+6=0,则2x÷8y=_____.
【答案】
【分析】此题考查的是幂的运算性质,掌握幂的乘方的逆运算、同底数幂的除法和负指数幂的性质是解决此题的关键.
根据已知条件,先求出x﹣3y=﹣3,然后根据幂的乘方的逆运算和同底数幂的除法即可求出结论.
【详解】
解:2x﹣6y+6=0,
2(x﹣3y)=﹣6,
x﹣3y=﹣3,
∴2x÷8y=2x÷23y=2x﹣3y=2﹣3=.
故答案为:.
13、若(am+1bn+2)(a2n﹣1b2n)=a5b3,则求m+n的值=__________.
解:(am+1bn+2)(a2n﹣1b2n)=am+1×a2n﹣1×bn+2×b2n
=am+1+2n﹣1×bn+2+2n
=am+2nb3n+2=a5b3.
∴m+2n=5,3n+2=3,解得:n=,m=,
m+n=.
14、若ma=2,mb=3,mc=4,则m2a+b﹣c= .
解:∵ma=2,mb=3,mc=4,
∴m2a+b﹣c=(ma)2 mb÷mc=4×3÷4=3.
故答案为:3.
15、(2020春 玄武区期中)233、418、810的大小关系是(用>号连接) .
【分析】直接利用幂的乘方运算法则将原式变形,进而比较得出答案.
【解答】解:∵233、418=236、810=(23)10=230,
∴236>233>230,
∴418>233>810.
16、将一副直角三角板如图摆放,点A落在边上,,则______.
【答案】75°
【分析】
如图,设AB与EF的交点为G,先根据平行的性质,得到∠AGE=∠F=45°,再根据外角定理得到∠1=30°+45°=75°.
【详解】
如图,设AB与EF的交点为G.
∵AB//BF
∴∠AGE=∠F=45°(两直线平行,同位角相等)
∴∠1=30°+45°=75°(三角形外角定理)
故答案为:75°.
17、(2020春 高新区期中)如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD= .
【解析】∵AB∥CD,∴∠ABE=∠4,∠1=∠2,
∵∠BED=90°,∠BED=∠4+∠EDC,∴∠ABE+∠EDC=90°,
∵BF平分∠ABE,DF平分∠CDE,∴∠1+∠3=45°,
∵∠5=∠2+∠3,∴∠5=∠1+∠3=45°,即∠BFD=45°,
故答案为:45°.
18、阅读材料:①1的任何次幂都等于1;②﹣1的奇数次幂都等于﹣1;③﹣1的偶数次幂都等于1;
④任何不等于零的数的零次幂都等于1,
试根据以上材料探索使等式(2x+3)x+2016=1成立的x的值为 .
解:①当2x+3=1时,解得:x=﹣1,此时x+2016=2015,
则(2x+3)x+2016=12015=1,所以x=﹣1.
②当2x+3=﹣1时,解得:x=﹣2,此时x+2016=2014,
则(2x+3)x+2016=(﹣1)2014=1,所以x=﹣2.
③当x+2016=0时,x=﹣2016,此时2x+3=﹣4029,
则(2x+3)x+2016=(﹣4029)0=1,所以x=﹣2016.
综上所述,当x=﹣1,或x=﹣2,或x=﹣2016时,代数式(2x+3)x+2016的值为1.
故答案为:﹣1或﹣2或﹣2016.
三、解答题
19、(2019春 漳浦县期中)计算
(1)(m﹣n)2 (n﹣m)3 (n﹣m)4 (2)(b2n)3(b3)4n÷(b5)n+1
(3)(a2)3﹣a3 a3+(2a3)2; (4)(﹣4am+1)3÷[2(2am)2 a].
【分析】(1)根据同底数幂的乘法计算即可;
(2)根据幂的乘方和同底数幂的除法计算即可;
(3)根据幂的乘方、同底数幂的乘法和合并同类项解答即可;
(4)根据积的乘方和同底数幂的除法计算即可.
【解答】解:(1)(m﹣n)2 (n﹣m)3 (n﹣m)4=(n﹣m)2+3+4=(n﹣m)9;
(2)(b2n)3(b3)4n÷(b5)n+1=b6n b12n÷b5n+5=b6n+12n﹣5n﹣5=b13n﹣5;
(3)(a2)3﹣a3 a3+(2a3)2=a6﹣a6+4a6=4a6;
(4)(﹣4am+1)3÷[2(2am)2 a]=﹣64a3m+3÷8a2m+1=﹣8am+2
20、(2021春 仪征市期中)(1)已知10m=5,10n=2,求103m+2n的值;
(2)已知8m÷4n=16,求(﹣3)2n﹣3m的值.
【分析】(1)逆向运用同底数幂的乘法法则以及幂的乘方运算法则计算即可;
(2)逆向运用同底数幂的除法法则以及幂的乘方运算法则计算即可.
【解答】解:(1)∵10m=5,10n=2,
∴103m+2n=(10m)3 (10n)2=53×22=125×4=500;
(2)∵8m÷4n=23m÷22n=23m﹣2n=16=24,
∴3m﹣2n=4,
∴2n﹣3m=﹣4,
∴(﹣3)2n﹣3m.
21、(2020苏州七年级期中)已知:如图,,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:;
(2)若∠BFE=110°,∠A=60°,求∠B的度数.
【答案】(1)见详解;(2)50°.
【分析】
(1)由,可知∠A=∠C ,然后等量代换得到∠C=∠1,利用同位角相等两直线平行即可得证;
(2)由EF与OC平行,利用两直线平行同旁内角互补得到∠BFE+∠DOC=180°,然后通过三角形内角和即可求出∠B的度数.
【详解】
(1)证明:∵AB∥CD,∴∠A=∠C ,
又∵∠1=∠A,∴∠C=∠1,∴FE∥OC;
(2)解:∵FE∥OC,∴∠BFE+∠DOC=180°,
又∵∠BFE=110°,∴∠DOC=180°-110°=70°,∴∠AOB=∠DOC=70°,
∵∠A=60°,∴∠B=180°-60°-70°=50°.
22、(2020·扬中市期中)如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)画一个△BCP(要求各顶点在格点上,P不与A点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共________个.
【答案】(1)答案见解析;(2)答案见解析;(3)14.
【分析】用到的知识点为:三角形一边上的高为这边所对的顶点向这边所引的垂线段;图形的平移要归结为各顶点的平移,平行线见距离处处相等.
(1)过点A作AG⊥BC,交CB的延长线于点G,AG就是所求的△ABC中BC边上的高;
(2)把△ABC的三个顶点向右平移6格,再向上平移3格即可得到所求的△DEF;
(3)过A作BC的平行线与网格的交点(除A外都满足条件),过F作BC的平行线与网格的所有交点都满足条件.
【详解】解:(1)如图所示;
(2)如图所示;
如图所示,AG就是所求的△ABC中BC边上的高.
(3)如图所示,l1、l2和网格的交点除A外都满足条件,一共有14个点.
故答案为:14.
23、(2020泰州七年级期中)如图,在△ABC中,AE为边BC上的高,点D为边BC上的一点,连接AD.
(1)当AD为边BC上的中线时.若AE=4,△ABC的面积为24,求CD的长;
(2)当AD为∠BAC的角平分线时.
①若∠C =65°,∠B =35°,求∠DAE的度数;
②若∠C-∠B =20°,则∠DAE = °.
【答案】(1)6 ;(2)①15°;②10.
【分析】本题考查三角形的面积,三角形的中线与高等知识,解题的关键是熟练掌握基本知识,属于中基础题.
(1)利用三角形的面积公式求出BC即可解决问题;
(2)①根据三角形内角和求出∠BAC和∠CAE的度数,然后根据角平分线的定义求得∠CAD的度数,从而求解;
②设∠C=x°,则∠B=(x+20)°,然后根据三角形内角和用含x的式子表示出∠BAC和∠CAE的度数,然后根据角平分线的定义求得∠CAD的度数,从而求解.
【详解】
解:(1)由题意可知:AE⊥BC,AE=4,△ABC的面积为24,
∴×BC×AE=24,∴×BC×4=24,∴BC=12,
∵AD是△ABC的中线,∴CD=BC=6,
(2)①在△ABC中,∠BAC=180°-∠C-∠B =80°,
在△AEC中,∵AE⊥BC∴∠CAE=180°-90°-∠C=25°
∵AD为∠BAC的角平分线∴∠CAD= ,∴∠DAE的度数为∠CAD -∠CAE =15°
②设∠C=x°,则∠B=(x+20)°
在△ABC中,∠BAC=180°-∠C-∠B =(160-2x)°,
在△AEC中,∵AE⊥BC∴∠CAE=180°-90°-∠C=(90-x)°
∵AD为∠BAC的角平分线∴∠CAD=
∴∠DAE的度数为∠CAE- ∠CAD =10°
故答案为:10.
24、(2021春 安庆期末)规定两数a,b之间的种运算,记作(a,b):如果ac=b,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:(5,125)= ;(5,1)= ;(2,)= ;
(2)小明在研究这种运算时发现一个特例:对任意的正整数n,(3n,4n)=(3,4).小明给了如下的 证明:设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n,所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4)请根据以上规律:计算:(16,10000)﹣(64,1000000).
(3)证明下面这个等式:(3,20)﹣(3,4)=(3,5).
【分析】(1)根据题目中的规定,进行运算即可得出结果;
(2)(16,10000)可转化为(24,104),(64,1000000)可转化为(26,106),从而可求解;
(3)设(3,20)=x,(3,4)=y,则3x=20,3y=4,从而可得3x÷3y=5,得3x﹣y=5,即有(3,5)=x﹣y,从而得证.
【解答】解:(1)∵53=125,∴(5,125)=3;
∵50=1,∴(5,1)=0;
∵,∴(2,)=﹣2.
故答案为:3,0,﹣2;
(2)(16,10000)﹣(64,1000000)
=(24,104)﹣(26,106)
=(2,10)﹣(2,10)
=0;
(3)证明:设(3,20)=x,(3,4)=y,则3x=20,3y=4,
∴3x÷3y=20÷4=5,
∴3x﹣y=5,
∴(3,5)=x﹣y,
又∵(3,20)﹣(3,4)=x﹣y,
∴(3,20)﹣(3,4)=(3,5)
25、(2021春 崇川区期末)在中,是的角平分线,为边上一点,,垂足为,平分交于点.
(1)如图1,若,延长、交于点,.
①用含的式子表示为 ;
②求证:;
(2)如图2,,延长,交于点,请用等式表示与的数量关系,并证明.
【分析】(1)①根据三角形的内角和定理和角平分线的定义即可得到结论;
②根据垂直的定义得到,求得,根据角平分线的定义得到,求得,于是得到结论;
(2)设,,根据角平分线的定义得到,,求得①,②,于是得到结论.
【解析】(1)①,,
,
平分,,
故答案为:;
②证明:,,,
,,
,
,,,
是的角平分线,,
,;
(2),
证明:平分,平分,
设,,,,
,,
,①,
中,,
中,,
,②,
由①和②得:,.
26、(21-22广东深圳福田区红岭中学八上期末)点E在射线DA上,点F、G为射线BC上两个动点,满足
∠DBF=∠DEF,∠BDG=∠BGD,DG平分∠BDE.
(1)如图1,当点G在F右侧时,求证:BD∥EF;
(2)如图2,当点G在F左侧时,求证:∠DGE=∠BDG+∠FEG;
(3)如图3,在(2)的条件下,P为BD延长线上一点,DM平分∠BDG,交BC于点M,DN平分
∠PDM,交EF于点N,连接NG,若DG⊥NG,∠B﹣∠DNG=∠EDN,则∠B的度数为 .
【分析】(1)通过证明∠DBF=∠EFG,利用同位角相等,两直线平行即可得出结论;
(2)过点E作GH∥BD,交AD于点H,利用(1)的结论和平行线的性质即可得出结论;
(3)设∠BDM=∠MDG=α,则∠BDG=∠EDG=∠DGB=2α,∠PDE=180°﹣4α,∠PDM=180°﹣α;利用已知条件用含α的式子表示∠PDN,∠EDN,∠GDN,∠DNG,再利用∠B﹣∠DNG=∠EDN,得到关于α的方程,解方程求得α的值,则∠B=180°﹣4α,结论可求.
【解答】证明:(1)∵DG平分∠BDE,∴∠BDG=∠ADG.
又∵∠BDG=∠BGD,∴∠ADG=∠DGB.
∴AD∥BC.∴∠DEF=∠EFG.
∵∠DBF=∠DEF,∴∠DBF=∠EFG.∴BD∥EF.
(2)过点G作GH∥BD,交AD于点H,如图,
∵BD∥EF,∴GH∥EF.
∴∠BDG=∠DGH,∠GEF=∠HGE,
∵∠DGE=∠DGH+∠HGE,∴∠DGE=∠BDG+∠FEG.
(3)设∠BDM=∠MDG=α,则∠BDG=∠EDG=∠DGB=2α,∠PDE=180°﹣4α.
∴∠PDM=180°﹣α.
∵DN平分∠PDM,∴.
∴∠EDN=∠PDN ∠PDE=90°﹣﹣(180°﹣4α)=﹣90°.
∴∠GDN=∠MDN﹣∠MDG=90°﹣﹣α=90°﹣.
∵DG⊥ON,∴∠DNG=90°.∴∠DNG=90° (90° )=.
∵DE∥BF,∴∠B=∠PDE=180°﹣4α.
∵∠B﹣∠DNG=∠EDN,∴180° 4α =﹣90°,解得:α=30°.
∴∠B=180°﹣4α=60°,
故答案为:60°.
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、下列是四个汽车标志图案,其中可看作由“基本图案”经过平移得到的是( )
A. B. C. D.
2、(2020南通期末)若,则n=( )
A.2022 B.2021 C.2020 D.2019
3、(2020·淮阳市七年级期末)计算的结果为( )
A. B. C. D.2
4、(2020·山东德州市·八年级期末)已知,则的值是( )
A.48 B.16 C.12 D.8
5、(2021春 济阳区期末)如果a=(﹣99)0,b=(﹣0.1)﹣1,c=,那么a、b、c的大小关系为( )
A.a>b>c B.c>a>b C.a>c>b D.c>b>a
6、如图,△EFG 的三个顶点 E,G 和 F 分别在平行线 AB,CD 上,FH 平分∠EFG,交线段 EG 于 点 H,若∠AEF=36°,∠BEG=57°,则∠EHF 的大小为( )
A.105° B.75° C.90° D.95°
(6题) (7题) (8题)
7、(2020春 天宁区校级期中)如图,将长方形ABCD沿直线EF折叠到ED 'C 'F的位置,若∠DEF=70°,则∠BFC '的度数为( )
A.20° B.30° C.40° D.50°
8、(2020春 仪征市期中)如图在五边形ABCDE中,∠A=∠B=∠C=∠D,∠DEF=3∠AEF,则∠AFE度数是( )
A.45° B.60° C.72° D.无法确定
9、(2020春 常州期中)如图,将△ABC纸片沿DE折叠,点A的对应点为A’,若∠B=60°,∠C=80°,则∠1+∠2等于( )
A.40° B.60° C.80° D.140°
(9题) (10题)
10、(2020春 泰兴市校级期中)如图,在△ABC中,∠A=48°,∠ABC与∠ACD的平分线交于点,得∠;∠BC与∠CD的平分线相交于点,得∠;……;∠BC与∠CD的平分线交于点,要使∠的度数为整数,则n的最大值为( )
A.2 B.3 C.4 D.5
二、填空题
11、(2020·江西南昌市·七年级期中)计算的结果是_________.
12、(2020常州期末)已知2x﹣6y+6=0,则2x÷8y=_____.
13、若(am+1bn+2)(a2n﹣1b2n)=a5b3,则求m+n的值=__________.
14、若ma=2,mb=3,mc=4,则m2a+b﹣c= .
15、(2020春 玄武区期中)233、418、810的大小关系是(用>号连接) .
16、将一副直角三角板如图摆放,点A落在边上,,则______.
(16题) (17题)
17、(2020春 高新区期中)如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD= .
18、阅读材料:①1的任何次幂都等于1;②﹣1的奇数次幂都等于﹣1;③﹣1的偶数次幂都等于1;
④任何不等于零的数的零次幂都等于1,
试根据以上材料探索使等式(2x+3)x+2016=1成立的x的值为 .
三、解答题
19、(2019春 漳浦县期中)计算
(1)(m﹣n)2 (n﹣m)3 (n﹣m)4 (2)(b2n)3(b3)4n÷(b5)n+1
(3)(a2)3﹣a3 a3+(2a3)2; (4)(﹣4am+1)3÷[2(2am)2 a].
20、(2021春 仪征市期中)(1)已知10m=5,10n=2,求103m+2n的值;
(2)已知8m÷4n=16,求(﹣3)2n﹣3m的值.
21、(2020苏州七年级期中)已知:如图,,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:;
(2)若∠BFE=110°,∠A=60°,求∠B的度数.
22、(2020·扬中市期中)如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)画一个△BCP(要求各顶点在格点上,P不与A点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共________个.
23、(2020泰州七年级期中)如图,在△ABC中,AE为边BC上的高,点D为边BC上的一点,连接AD.
(1)当AD为边BC上的中线时.若AE=4,△ABC的面积为24,求CD的长;
(2)当AD为∠BAC的角平分线时.
①若∠C =65°,∠B =35°,求∠DAE的度数;
②若∠C-∠B =20°,则∠DAE = °.
24、(2021春 安庆期末)规定两数a,b之间的种运算,记作(a,b):如果ac=b,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:(5,125)= ;(5,1)= ;(2,)= ;
(2)小明在研究这种运算时发现一个特例:对任意的正整数n,(3n,4n)=(3,4).小明给了如下的 证明:设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n,所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4)请根据以上规律:计算:(16,10000)﹣(64,1000000).
(3)证明下面这个等式:(3,20)﹣(3,4)=(3,5).
25、(2021春 崇川区期末)在中,是的角平分线,为边上一点,,垂足为,平分交于点.
(1)如图1,若,延长、交于点,.
①用含的式子表示为 ;
②求证:;
(2)如图2,,延长,交于点,请用等式表示与的数量关系,并证明.
26、(21-22广东深圳福田区红岭中学八上期末)点E在射线DA上,点F、G为射线BC上两个动点,满足
∠DBF=∠DEF,∠BDG=∠BGD,DG平分∠BDE.
(1)如图1,当点G在F右侧时,求证:BD∥EF;
(2)如图2,当点G在F左侧时,求证:∠DGE=∠BDG+∠FEG;
(3)如图3,在(2)的条件下,P为BD延长线上一点,DM平分∠BDG,交BC于点M,DN平分
∠PDM,交EF于点N,连接NG,若DG⊥NG,∠B﹣∠DNG=∠EDN,则∠B的度数为 .
7~8章 阶段练(4)(培优)【平面图形的认识(二)、幂的运算】
-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、下列是四个汽车标志图案,其中可看作由“基本图案”经过平移得到的是( )
A. B. C. D.
【答案】B
【分析】
根据平移的概念观察即可
【详解】
解:由“基本图案”经过旋转得到
由“基本图案”经过平移得到
由“基本图案”经过翻折得到
不能由 “基本图案”经过平移得到
故选:B
2、(2020南通期末)若,则n=( )
A.2022 B.2021 C.2020 D.2019
【答案】A
【分析】本题考查了乘方的意义,以及同底数幂的乘法运算.注意:求n个相同因数乘积的运算,叫做乘方,乘方的结果叫做幂.
2020个2020相乘,可以写成,2020个2020相加,可以写成,计算即可得到答案.
【详解】∵,
,
∴原式左边,
即,∴.
故选:A.
3、(2020·淮阳市七年级期末)计算的结果为( )
A. B. C. D.2
【答案】B
【分析】本题考查了有理数的混合运算,解题的关键是合理利用同底数幂的乘法法则进行简便运算.
根据同底数幂的乘法法则运算即可.
【详解】
解:
=
=
=
=
故选B.
4、(2020·山东德州市·八年级期末)已知,则的值是( )
A.48 B.16 C.12 D.8
【答案】A
【分析】本题是对同底数幂乘除的考查,熟练掌握整式的乘除是解决本题的关键.
先把化成,再计算即可.
【详解】先把化成,
原式===48,
故选A.
5、(2021春 济阳区期末)如果a=(﹣99)0,b=(﹣0.1)﹣1,c=,那么a、b、c的大小关系为( )
A.a>b>c B.c>a>b C.a>c>b D.c>b>a
【分析】根据负整数指数次幂等于正整数指数次幂的倒数,任何非零数的零指数次幂等于1求出a、b、c,然后按照从大到小的顺序排列即可.
【解答】解:a=(﹣99)0=1,
b=(﹣0.1)﹣1=﹣10,
c=()﹣2=9,
所以c>a>b.
故选:B.
6、如图,△EFG 的三个顶点 E,G 和 F 分别在平行线 AB,CD 上,FH 平分∠EFG,交线段 EG 于 点 H,若∠AEF=36°,∠BEG=57°,则∠EHF 的大小为( )
A.105° B.75° C.90° D.95°
【答案】B
【分析】
首先根据∠AEF=36°,∠BEG=57°,求出∠FEH的大小;然后根据AB∥CD,求出∠EFG的大小,再根据FH平分∠EFG,求出∠EFH的大小;最后根据三角形内角和定理,求出∠EHF的大小为多少即可.
【详解】
解:∵∠AEF=36°,∠BEG=57°,∴∠FEH=180°-36°-57°=87°;
∵AB∥CD,∴∠EFG=∠AEF=36°,
∵FH平分∠EFG,∴∠EFH=∠EFG=×36°=18°,
∴∠EHF=180°-∠FEH-∠EFH=180°-87°-18°=75°.
故选:B.
7、(2020春 天宁区校级期中)如图,将长方形ABCD沿直线EF折叠到ED 'C 'F的位置,若∠DEF=70°,则∠BFC '的度数为( )
A.20° B.30° C.40° D.50°
解:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠DEF=∠EFB(两直线平行,内错角相等),
∵∠DEF=70°,
∴∠EFB=70°,
∵长方形ABCD沿直线EF折叠到ED'C'F的位置,
∴ED′∥FC′,∠D′EF=∠DEF=70°,
∴∠D′EF+∠C′FE=180°(两直线平行,同旁内角互补),
∴∠C′FE=110°,
∴∠BFC'=∠C′FE﹣∠EFB=110°﹣70°=40°,
故选:C.
8、(2020春 仪征市期中)如图在五边形ABCDE中,∠A=∠B=∠C=∠D,∠DEF=3∠AEF,则∠AFE度数是( )
A.45° B.60° C.72° D.无法确定
解:设∠A=∠B=∠C=∠D=x°,∠AEF=y°,则∠DEF=3y°,依题意有
4x+4y=540,
解得x+y=135,
则∠AFE=180°﹣135°=45°.
故选:A.
9、(2020春 常州期中)如图,将△ABC纸片沿DE折叠,点A的对应点为A’,若∠B=60°,∠C=80°,则∠1+∠2等于( )
A.40° B.60° C.80° D.140°
解:连接AA′.
∵∠B=60°,∠C=80°,
∴∠A=40°
∵∠2=∠EA′A+∠EAA′,∠1=∠DA′A+∠DAA′,∠BAC=∠EA′D,
∴∠1+∠2=∠EA′A+∠EAA′+∠DA′A+∠DAA′=∠EAD+∠EA′D=2∠EAD=80°,
故选:C.
10、(2020春 泰兴市校级期中)如图,在△ABC中,∠A=48°,∠ABC与∠ACD的平分线交于点,得∠;∠BC与∠CD的平分线相交于点,得∠;……;∠BC与∠CD的平分线交于点,要使∠的度数为整数,则n的最大值为( )
A.2 B.3 C.4 D.5
解:∵∠ABC与∠ACD的平分线交于点A1,
∴∠A1=180°﹣∠ACD﹣∠ACB﹣∠ABC
=180°﹣(∠ABC+∠A)﹣(180°﹣∠A﹣∠ABC)﹣∠ABC
=∠A
=;
同理可得∠A2=∠A1=,…
∴∠An=.
∴要使∠An的度数为整数,则n的最大值为4,此时∠A4=3°.
故选:C.
二、填空题
11、(2020·江西南昌市·七年级期中)计算的结果是_________.
【答案】
【分析】本题主要考查幂的运算法则,熟练掌握幂的运算法则是解答本题的关键.
先用同底数幂乘法逆运算将变为,再提公因数计算即可.
【详解】,
故答案为:
12、(2020常州期末)已知2x﹣6y+6=0,则2x÷8y=_____.
【答案】
【分析】此题考查的是幂的运算性质,掌握幂的乘方的逆运算、同底数幂的除法和负指数幂的性质是解决此题的关键.
根据已知条件,先求出x﹣3y=﹣3,然后根据幂的乘方的逆运算和同底数幂的除法即可求出结论.
【详解】
解:2x﹣6y+6=0,
2(x﹣3y)=﹣6,
x﹣3y=﹣3,
∴2x÷8y=2x÷23y=2x﹣3y=2﹣3=.
故答案为:.
13、若(am+1bn+2)(a2n﹣1b2n)=a5b3,则求m+n的值=__________.
解:(am+1bn+2)(a2n﹣1b2n)=am+1×a2n﹣1×bn+2×b2n
=am+1+2n﹣1×bn+2+2n
=am+2nb3n+2=a5b3.
∴m+2n=5,3n+2=3,解得:n=,m=,
m+n=.
14、若ma=2,mb=3,mc=4,则m2a+b﹣c= .
解:∵ma=2,mb=3,mc=4,
∴m2a+b﹣c=(ma)2 mb÷mc=4×3÷4=3.
故答案为:3.
15、(2020春 玄武区期中)233、418、810的大小关系是(用>号连接) .
【分析】直接利用幂的乘方运算法则将原式变形,进而比较得出答案.
【解答】解:∵233、418=236、810=(23)10=230,
∴236>233>230,
∴418>233>810.
16、将一副直角三角板如图摆放,点A落在边上,,则______.
【答案】75°
【分析】
如图,设AB与EF的交点为G,先根据平行的性质,得到∠AGE=∠F=45°,再根据外角定理得到∠1=30°+45°=75°.
【详解】
如图,设AB与EF的交点为G.
∵AB//BF
∴∠AGE=∠F=45°(两直线平行,同位角相等)
∴∠1=30°+45°=75°(三角形外角定理)
故答案为:75°.
17、(2020春 高新区期中)如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD= .
【解析】∵AB∥CD,∴∠ABE=∠4,∠1=∠2,
∵∠BED=90°,∠BED=∠4+∠EDC,∴∠ABE+∠EDC=90°,
∵BF平分∠ABE,DF平分∠CDE,∴∠1+∠3=45°,
∵∠5=∠2+∠3,∴∠5=∠1+∠3=45°,即∠BFD=45°,
故答案为:45°.
18、阅读材料:①1的任何次幂都等于1;②﹣1的奇数次幂都等于﹣1;③﹣1的偶数次幂都等于1;
④任何不等于零的数的零次幂都等于1,
试根据以上材料探索使等式(2x+3)x+2016=1成立的x的值为 .
解:①当2x+3=1时,解得:x=﹣1,此时x+2016=2015,
则(2x+3)x+2016=12015=1,所以x=﹣1.
②当2x+3=﹣1时,解得:x=﹣2,此时x+2016=2014,
则(2x+3)x+2016=(﹣1)2014=1,所以x=﹣2.
③当x+2016=0时,x=﹣2016,此时2x+3=﹣4029,
则(2x+3)x+2016=(﹣4029)0=1,所以x=﹣2016.
综上所述,当x=﹣1,或x=﹣2,或x=﹣2016时,代数式(2x+3)x+2016的值为1.
故答案为:﹣1或﹣2或﹣2016.
三、解答题
19、(2019春 漳浦县期中)计算
(1)(m﹣n)2 (n﹣m)3 (n﹣m)4 (2)(b2n)3(b3)4n÷(b5)n+1
(3)(a2)3﹣a3 a3+(2a3)2; (4)(﹣4am+1)3÷[2(2am)2 a].
【分析】(1)根据同底数幂的乘法计算即可;
(2)根据幂的乘方和同底数幂的除法计算即可;
(3)根据幂的乘方、同底数幂的乘法和合并同类项解答即可;
(4)根据积的乘方和同底数幂的除法计算即可.
【解答】解:(1)(m﹣n)2 (n﹣m)3 (n﹣m)4=(n﹣m)2+3+4=(n﹣m)9;
(2)(b2n)3(b3)4n÷(b5)n+1=b6n b12n÷b5n+5=b6n+12n﹣5n﹣5=b13n﹣5;
(3)(a2)3﹣a3 a3+(2a3)2=a6﹣a6+4a6=4a6;
(4)(﹣4am+1)3÷[2(2am)2 a]=﹣64a3m+3÷8a2m+1=﹣8am+2
20、(2021春 仪征市期中)(1)已知10m=5,10n=2,求103m+2n的值;
(2)已知8m÷4n=16,求(﹣3)2n﹣3m的值.
【分析】(1)逆向运用同底数幂的乘法法则以及幂的乘方运算法则计算即可;
(2)逆向运用同底数幂的除法法则以及幂的乘方运算法则计算即可.
【解答】解:(1)∵10m=5,10n=2,
∴103m+2n=(10m)3 (10n)2=53×22=125×4=500;
(2)∵8m÷4n=23m÷22n=23m﹣2n=16=24,
∴3m﹣2n=4,
∴2n﹣3m=﹣4,
∴(﹣3)2n﹣3m.
21、(2020苏州七年级期中)已知:如图,,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:;
(2)若∠BFE=110°,∠A=60°,求∠B的度数.
【答案】(1)见详解;(2)50°.
【分析】
(1)由,可知∠A=∠C ,然后等量代换得到∠C=∠1,利用同位角相等两直线平行即可得证;
(2)由EF与OC平行,利用两直线平行同旁内角互补得到∠BFE+∠DOC=180°,然后通过三角形内角和即可求出∠B的度数.
【详解】
(1)证明:∵AB∥CD,∴∠A=∠C ,
又∵∠1=∠A,∴∠C=∠1,∴FE∥OC;
(2)解:∵FE∥OC,∴∠BFE+∠DOC=180°,
又∵∠BFE=110°,∴∠DOC=180°-110°=70°,∴∠AOB=∠DOC=70°,
∵∠A=60°,∴∠B=180°-60°-70°=50°.
22、(2020·扬中市期中)如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)画一个△BCP(要求各顶点在格点上,P不与A点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共________个.
【答案】(1)答案见解析;(2)答案见解析;(3)14.
【分析】用到的知识点为:三角形一边上的高为这边所对的顶点向这边所引的垂线段;图形的平移要归结为各顶点的平移,平行线见距离处处相等.
(1)过点A作AG⊥BC,交CB的延长线于点G,AG就是所求的△ABC中BC边上的高;
(2)把△ABC的三个顶点向右平移6格,再向上平移3格即可得到所求的△DEF;
(3)过A作BC的平行线与网格的交点(除A外都满足条件),过F作BC的平行线与网格的所有交点都满足条件.
【详解】解:(1)如图所示;
(2)如图所示;
如图所示,AG就是所求的△ABC中BC边上的高.
(3)如图所示,l1、l2和网格的交点除A外都满足条件,一共有14个点.
故答案为:14.
23、(2020泰州七年级期中)如图,在△ABC中,AE为边BC上的高,点D为边BC上的一点,连接AD.
(1)当AD为边BC上的中线时.若AE=4,△ABC的面积为24,求CD的长;
(2)当AD为∠BAC的角平分线时.
①若∠C =65°,∠B =35°,求∠DAE的度数;
②若∠C-∠B =20°,则∠DAE = °.
【答案】(1)6 ;(2)①15°;②10.
【分析】本题考查三角形的面积,三角形的中线与高等知识,解题的关键是熟练掌握基本知识,属于中基础题.
(1)利用三角形的面积公式求出BC即可解决问题;
(2)①根据三角形内角和求出∠BAC和∠CAE的度数,然后根据角平分线的定义求得∠CAD的度数,从而求解;
②设∠C=x°,则∠B=(x+20)°,然后根据三角形内角和用含x的式子表示出∠BAC和∠CAE的度数,然后根据角平分线的定义求得∠CAD的度数,从而求解.
【详解】
解:(1)由题意可知:AE⊥BC,AE=4,△ABC的面积为24,
∴×BC×AE=24,∴×BC×4=24,∴BC=12,
∵AD是△ABC的中线,∴CD=BC=6,
(2)①在△ABC中,∠BAC=180°-∠C-∠B =80°,
在△AEC中,∵AE⊥BC∴∠CAE=180°-90°-∠C=25°
∵AD为∠BAC的角平分线∴∠CAD= ,∴∠DAE的度数为∠CAD -∠CAE =15°
②设∠C=x°,则∠B=(x+20)°
在△ABC中,∠BAC=180°-∠C-∠B =(160-2x)°,
在△AEC中,∵AE⊥BC∴∠CAE=180°-90°-∠C=(90-x)°
∵AD为∠BAC的角平分线∴∠CAD=
∴∠DAE的度数为∠CAE- ∠CAD =10°
故答案为:10.
24、(2021春 安庆期末)规定两数a,b之间的种运算,记作(a,b):如果ac=b,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:(5,125)= ;(5,1)= ;(2,)= ;
(2)小明在研究这种运算时发现一个特例:对任意的正整数n,(3n,4n)=(3,4).小明给了如下的 证明:设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n,所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4)请根据以上规律:计算:(16,10000)﹣(64,1000000).
(3)证明下面这个等式:(3,20)﹣(3,4)=(3,5).
【分析】(1)根据题目中的规定,进行运算即可得出结果;
(2)(16,10000)可转化为(24,104),(64,1000000)可转化为(26,106),从而可求解;
(3)设(3,20)=x,(3,4)=y,则3x=20,3y=4,从而可得3x÷3y=5,得3x﹣y=5,即有(3,5)=x﹣y,从而得证.
【解答】解:(1)∵53=125,∴(5,125)=3;
∵50=1,∴(5,1)=0;
∵,∴(2,)=﹣2.
故答案为:3,0,﹣2;
(2)(16,10000)﹣(64,1000000)
=(24,104)﹣(26,106)
=(2,10)﹣(2,10)
=0;
(3)证明:设(3,20)=x,(3,4)=y,则3x=20,3y=4,
∴3x÷3y=20÷4=5,
∴3x﹣y=5,
∴(3,5)=x﹣y,
又∵(3,20)﹣(3,4)=x﹣y,
∴(3,20)﹣(3,4)=(3,5)
25、(2021春 崇川区期末)在中,是的角平分线,为边上一点,,垂足为,平分交于点.
(1)如图1,若,延长、交于点,.
①用含的式子表示为 ;
②求证:;
(2)如图2,,延长,交于点,请用等式表示与的数量关系,并证明.
【分析】(1)①根据三角形的内角和定理和角平分线的定义即可得到结论;
②根据垂直的定义得到,求得,根据角平分线的定义得到,求得,于是得到结论;
(2)设,,根据角平分线的定义得到,,求得①,②,于是得到结论.
【解析】(1)①,,
,
平分,,
故答案为:;
②证明:,,,
,,
,
,,,
是的角平分线,,
,;
(2),
证明:平分,平分,
设,,,,
,,
,①,
中,,
中,,
,②,
由①和②得:,.
26、(21-22广东深圳福田区红岭中学八上期末)点E在射线DA上,点F、G为射线BC上两个动点,满足
∠DBF=∠DEF,∠BDG=∠BGD,DG平分∠BDE.
(1)如图1,当点G在F右侧时,求证:BD∥EF;
(2)如图2,当点G在F左侧时,求证:∠DGE=∠BDG+∠FEG;
(3)如图3,在(2)的条件下,P为BD延长线上一点,DM平分∠BDG,交BC于点M,DN平分
∠PDM,交EF于点N,连接NG,若DG⊥NG,∠B﹣∠DNG=∠EDN,则∠B的度数为 .
【分析】(1)通过证明∠DBF=∠EFG,利用同位角相等,两直线平行即可得出结论;
(2)过点E作GH∥BD,交AD于点H,利用(1)的结论和平行线的性质即可得出结论;
(3)设∠BDM=∠MDG=α,则∠BDG=∠EDG=∠DGB=2α,∠PDE=180°﹣4α,∠PDM=180°﹣α;利用已知条件用含α的式子表示∠PDN,∠EDN,∠GDN,∠DNG,再利用∠B﹣∠DNG=∠EDN,得到关于α的方程,解方程求得α的值,则∠B=180°﹣4α,结论可求.
【解答】证明:(1)∵DG平分∠BDE,∴∠BDG=∠ADG.
又∵∠BDG=∠BGD,∴∠ADG=∠DGB.
∴AD∥BC.∴∠DEF=∠EFG.
∵∠DBF=∠DEF,∴∠DBF=∠EFG.∴BD∥EF.
(2)过点G作GH∥BD,交AD于点H,如图,
∵BD∥EF,∴GH∥EF.
∴∠BDG=∠DGH,∠GEF=∠HGE,
∵∠DGE=∠DGH+∠HGE,∴∠DGE=∠BDG+∠FEG.
(3)设∠BDM=∠MDG=α,则∠BDG=∠EDG=∠DGB=2α,∠PDE=180°﹣4α.
∴∠PDM=180°﹣α.
∵DN平分∠PDM,∴.
∴∠EDN=∠PDN ∠PDE=90°﹣﹣(180°﹣4α)=﹣90°.
∴∠GDN=∠MDN﹣∠MDG=90°﹣﹣α=90°﹣.
∵DG⊥ON,∴∠DNG=90°.∴∠DNG=90° (90° )=.
∵DE∥BF,∴∠B=∠PDE=180°﹣4α.
∵∠B﹣∠DNG=∠EDN,∴180° 4α =﹣90°,解得:α=30°.
∴∠B=180°﹣4α=60°,
故答案为:60°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
