2021-2022学年苏科版七年级数学下册9.3多项式乘多项式提优训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册9.3多项式乘多项式提优训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 258.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 00:00:00 | ||
图片预览


文档简介
学习-----好资料
学习-----好资料
9.3 多项式乘多项式 提优训练
一、单选题
1.计算(a+3)(﹣a+1)的结果是( )
A.﹣a2﹣2a+3 B.﹣a2+4a+3 C.﹣a2+4a﹣3 D.a2﹣2a﹣3
2若的乘积中不含的二次项和一次项,则常数、的值为
A. , B. ,
C. , D. ,
3.如图,是一楼房的平面图,下列式子中不能表示它的面积的是( )
A. B. C. D.
4.下列计算错误的是( )
A. (x+1)(x+4)=x2+5x+4 B. (m-2)(m+3)=m2+m-6
C. (x-3)(x-6)=x2-9x+18 D. (y+4)(y-5)=y2+9y-20
5.展开后不含和的项,则、的值为( )
A. B. C. D.
6.用图1的面积可以验证多项式的乘法运算,那么用图2的面积可以验证的乘法运算是( )
A. B.
C. D.
7.用下列各式分别表示图中阴影部分的面积,其中表示正确的有( )
①;②;③;④;
A.4个 B.3个 C.2个 D.1个
8.观察下列多项式的乘法计算:
①(x+3)(x+4)=x2+7x+12;②(x+3)(x﹣4)=x2﹣x﹣12;
③(x﹣3)(x+4)=x2+x﹣12;④(x﹣3)(x﹣4)=x2﹣7x+12
根据你发现的规律,若(x+p)(x+q)=x2﹣8x+15,则p+q的值为( )
A. ﹣8 B. ﹣2 C. 2 D. 8
9.下列有四个结论,其中正确的是( )
①若(x -1) x+1 = 1,则 x 只能是 2;
②若(x -1)(x2 + ax +1)的运算结果中不含 x2项,则 a=1;
③若(2x - 4) - 2(x - 3) -1 有意义,则 x 的取值范围是 x ≠ 2 ;
④若 4x = a,8y = b,则22x-3y 可表示为
A. ②④ B. ②③④ C. ①③④ D. ①②③④
10已知多项式与的乘积展开式中不含的一次项,且常数项为,则的值为
A. B. C. D.
二、填空题
11、计算:(a+3)(2a﹣6)= .
12、已知(x+a)(x2﹣x)的展开式中不含x2项,则a= .
13、已知2x=4,2y=8,则(x﹣2)(y﹣2)+3(xy﹣3)的值为 .
14、若三角形的一边长为2a+4,这边上的高为2a﹣3,则此三角形的面积为 .
15.(2021·全国九年级专题练习)如图,现有A,C两类正方形卡片和B类长方形卡片各若干张,用它们可以拼成一些新的长方形.如果要拼成一个长为(3a+b),宽为(a+2b)的长方形,那么需要B类长方形卡片__张.
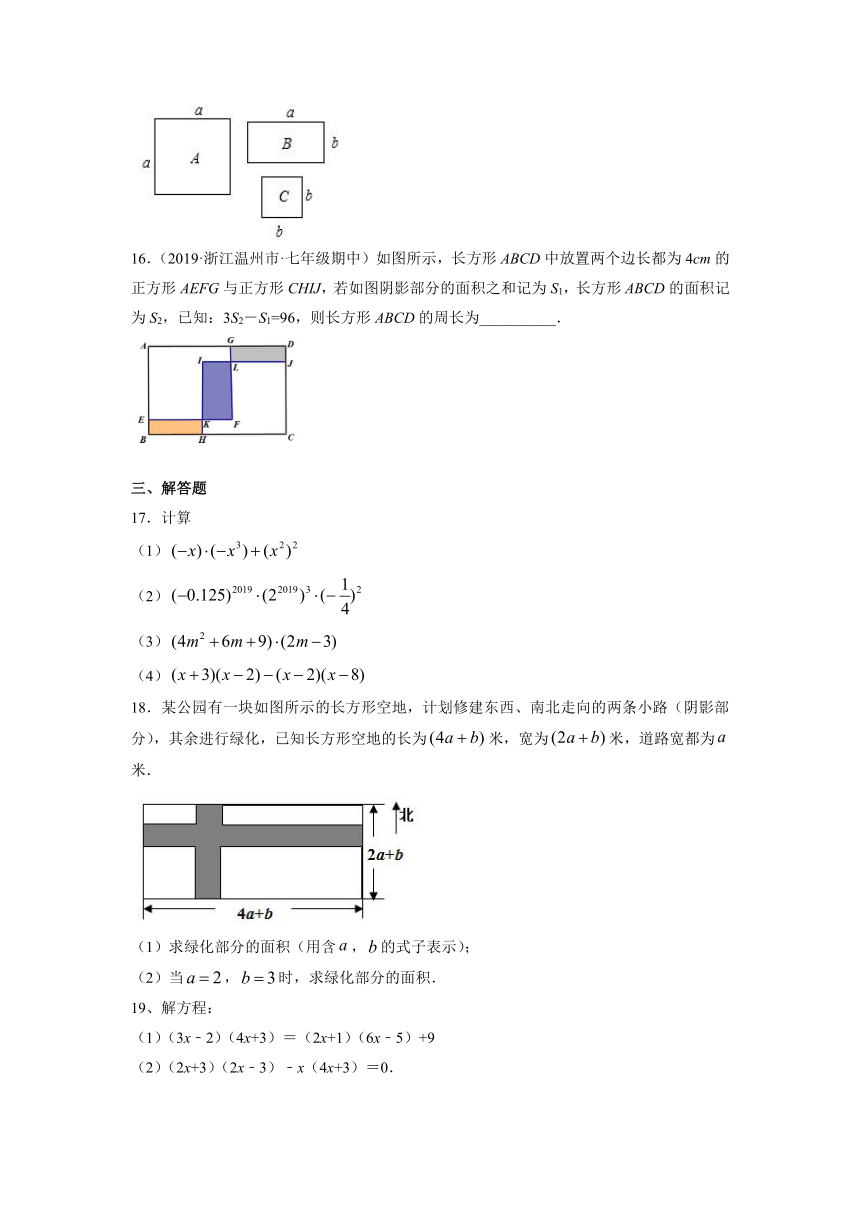
16.(2019·浙江温州市·七年级期中)如图所示,长方形ABCD中放置两个边长都为4cm的正方形AEFG与正方形CHIJ,若如图阴影部分的面积之和记为S1,长方形ABCD的面积记为S2,已知:3S2-S1=96,则长方形ABCD的周长为__________.
三、解答题
17.计算
(1)
(2)
(3)
(4)
18.某公园有一块如图所示的长方形空地,计划修建东西、南北走向的两条小路(阴影部分),其余进行绿化,已知长方形空地的长为米,宽为米,道路宽都为米.
(1)求绿化部分的面积(用含,的式子表示);
(2)当,时,求绿化部分的面积.
19、解方程:
(1)(3x﹣2)(4x+3)=(2x+1)(6x﹣5)+9
(2)(2x+3)(2x﹣3)﹣x(4x+3)=0.
20、(1)运用多项式乘法,计算下列各题:
①(x+3)(x+4)= ; ②(x+3)(x﹣4)= ;
③(x﹣3)(x+4)= ;④(x﹣3)(x﹣4)= ;
根据你所发现的规律,你能直接写出(x+a)(x+b)的结果吗?
(2)请运用此规律进行以下运算:
①(x+5)(x+7) ②(x+8)(x﹣4)
③(a﹣3)(a+5) ④(y2﹣2)(y2﹣4)
21、先阅读材料,再解答问题:
例:已知x=123456789×123456786,y=123456788×123456787,试比较x、y的大小.
解:设123456788=a,则x=(a+1)(a﹣2)=a2﹣a﹣2,y=a(a﹣1)=a2﹣a,
∵x﹣y=(a2﹣a﹣2)﹣(a2﹣a)=﹣2,∴x<y.
问题:已知x=20182018×20182022﹣20182019×20182021,
y=20182019×20182023﹣20182020×20182022,
试比较x、y的大小.
参考答案
1.A 2.A 3.D 4.D 5.A 6.A 7.A 8.D 9.A 10.A
11、2a2﹣18.
12、1.
13、9.
14、2a2+a﹣6.
15.7
16.24
17.(1);(2);(3);(4)
【详解】
(1)原式
(2)原式
(3)原式
(4)原式
18(1)平方米;(2)45平方米
【详解】
解:(1)由题意,得,
所以绿化部分的面积是平方米.
(2)当,时,原式,
所以绿化部分的面积为平方米.
19、解方程:解:(1)12x2+9x﹣8x﹣6=12x2﹣10x+6x﹣5+9,
12x2+9x﹣8x﹣12x2+10x﹣6x=﹣5+9+6,
5x=10,
x=2;
(2)4x2﹣9﹣4x2﹣3x=0,
4x2﹣4x2﹣3x=9,
﹣3x=9,
x=﹣3.
20、解:(1)①(x+3)(x+4)=x2+7x+12;
②(x+3)(x﹣4)=x2﹣x﹣12;
③(x﹣3)(x+4)=x2+x﹣12;
④(x﹣3)(x﹣4)=x2﹣7x+12
则(x+a)(x+b)=x2+(a+b)x+ab,
故答案为:①x2+7x+12;②x2﹣x﹣12;③x2+x﹣12;④x2﹣7x+12;
(2)请运用此规律进行以下运算:
①(x+5)(x+7)=x2+12x+35,
②(x+8)(x﹣4)=﹣2x+4x﹣32=+2x﹣32,
③(a﹣3)(a+5)=a2+2a﹣15,
④(y2﹣2)(y2﹣4)=y4﹣6y2+8.
21、
解:设20182019=a,
那么x=(a﹣1)(a+3)﹣(a+2)a=﹣3,
y=a(a+4)﹣(a+1)(a+3)=﹣3,
所以x=y.
更多精品文档
更多精品文档
学习-----好资料
9.3 多项式乘多项式 提优训练
一、单选题
1.计算(a+3)(﹣a+1)的结果是( )
A.﹣a2﹣2a+3 B.﹣a2+4a+3 C.﹣a2+4a﹣3 D.a2﹣2a﹣3
2若的乘积中不含的二次项和一次项,则常数、的值为
A. , B. ,
C. , D. ,
3.如图,是一楼房的平面图,下列式子中不能表示它的面积的是( )
A. B. C. D.
4.下列计算错误的是( )
A. (x+1)(x+4)=x2+5x+4 B. (m-2)(m+3)=m2+m-6
C. (x-3)(x-6)=x2-9x+18 D. (y+4)(y-5)=y2+9y-20
5.展开后不含和的项,则、的值为( )
A. B. C. D.
6.用图1的面积可以验证多项式的乘法运算,那么用图2的面积可以验证的乘法运算是( )
A. B.
C. D.
7.用下列各式分别表示图中阴影部分的面积,其中表示正确的有( )
①;②;③;④;
A.4个 B.3个 C.2个 D.1个
8.观察下列多项式的乘法计算:
①(x+3)(x+4)=x2+7x+12;②(x+3)(x﹣4)=x2﹣x﹣12;
③(x﹣3)(x+4)=x2+x﹣12;④(x﹣3)(x﹣4)=x2﹣7x+12
根据你发现的规律,若(x+p)(x+q)=x2﹣8x+15,则p+q的值为( )
A. ﹣8 B. ﹣2 C. 2 D. 8
9.下列有四个结论,其中正确的是( )
①若(x -1) x+1 = 1,则 x 只能是 2;
②若(x -1)(x2 + ax +1)的运算结果中不含 x2项,则 a=1;
③若(2x - 4) - 2(x - 3) -1 有意义,则 x 的取值范围是 x ≠ 2 ;
④若 4x = a,8y = b,则22x-3y 可表示为
A. ②④ B. ②③④ C. ①③④ D. ①②③④
10已知多项式与的乘积展开式中不含的一次项,且常数项为,则的值为
A. B. C. D.
二、填空题
11、计算:(a+3)(2a﹣6)= .
12、已知(x+a)(x2﹣x)的展开式中不含x2项,则a= .
13、已知2x=4,2y=8,则(x﹣2)(y﹣2)+3(xy﹣3)的值为 .
14、若三角形的一边长为2a+4,这边上的高为2a﹣3,则此三角形的面积为 .
15.(2021·全国九年级专题练习)如图,现有A,C两类正方形卡片和B类长方形卡片各若干张,用它们可以拼成一些新的长方形.如果要拼成一个长为(3a+b),宽为(a+2b)的长方形,那么需要B类长方形卡片__张.
16.(2019·浙江温州市·七年级期中)如图所示,长方形ABCD中放置两个边长都为4cm的正方形AEFG与正方形CHIJ,若如图阴影部分的面积之和记为S1,长方形ABCD的面积记为S2,已知:3S2-S1=96,则长方形ABCD的周长为__________.
三、解答题
17.计算
(1)
(2)
(3)
(4)
18.某公园有一块如图所示的长方形空地,计划修建东西、南北走向的两条小路(阴影部分),其余进行绿化,已知长方形空地的长为米,宽为米,道路宽都为米.
(1)求绿化部分的面积(用含,的式子表示);
(2)当,时,求绿化部分的面积.
19、解方程:
(1)(3x﹣2)(4x+3)=(2x+1)(6x﹣5)+9
(2)(2x+3)(2x﹣3)﹣x(4x+3)=0.
20、(1)运用多项式乘法,计算下列各题:
①(x+3)(x+4)= ; ②(x+3)(x﹣4)= ;
③(x﹣3)(x+4)= ;④(x﹣3)(x﹣4)= ;
根据你所发现的规律,你能直接写出(x+a)(x+b)的结果吗?
(2)请运用此规律进行以下运算:
①(x+5)(x+7) ②(x+8)(x﹣4)
③(a﹣3)(a+5) ④(y2﹣2)(y2﹣4)
21、先阅读材料,再解答问题:
例:已知x=123456789×123456786,y=123456788×123456787,试比较x、y的大小.
解:设123456788=a,则x=(a+1)(a﹣2)=a2﹣a﹣2,y=a(a﹣1)=a2﹣a,
∵x﹣y=(a2﹣a﹣2)﹣(a2﹣a)=﹣2,∴x<y.
问题:已知x=20182018×20182022﹣20182019×20182021,
y=20182019×20182023﹣20182020×20182022,
试比较x、y的大小.
参考答案
1.A 2.A 3.D 4.D 5.A 6.A 7.A 8.D 9.A 10.A
11、2a2﹣18.
12、1.
13、9.
14、2a2+a﹣6.
15.7
16.24
17.(1);(2);(3);(4)
【详解】
(1)原式
(2)原式
(3)原式
(4)原式
18(1)平方米;(2)45平方米
【详解】
解:(1)由题意,得,
所以绿化部分的面积是平方米.
(2)当,时,原式,
所以绿化部分的面积为平方米.
19、解方程:解:(1)12x2+9x﹣8x﹣6=12x2﹣10x+6x﹣5+9,
12x2+9x﹣8x﹣12x2+10x﹣6x=﹣5+9+6,
5x=10,
x=2;
(2)4x2﹣9﹣4x2﹣3x=0,
4x2﹣4x2﹣3x=9,
﹣3x=9,
x=﹣3.
20、解:(1)①(x+3)(x+4)=x2+7x+12;
②(x+3)(x﹣4)=x2﹣x﹣12;
③(x﹣3)(x+4)=x2+x﹣12;
④(x﹣3)(x﹣4)=x2﹣7x+12
则(x+a)(x+b)=x2+(a+b)x+ab,
故答案为:①x2+7x+12;②x2﹣x﹣12;③x2+x﹣12;④x2﹣7x+12;
(2)请运用此规律进行以下运算:
①(x+5)(x+7)=x2+12x+35,
②(x+8)(x﹣4)=﹣2x+4x﹣32=+2x﹣32,
③(a﹣3)(a+5)=a2+2a﹣15,
④(y2﹣2)(y2﹣4)=y4﹣6y2+8.
21、
解:设20182019=a,
那么x=(a﹣1)(a+3)﹣(a+2)a=﹣3,
y=a(a+4)﹣(a+1)(a+3)=﹣3,
所以x=y.
更多精品文档
更多精品文档
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
