2021-2022学年苏科版七年级数学下册7~8章阶段练(1)(基础)(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册7~8章阶段练(1)(基础)(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 834.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 23:18:03 | ||
图片预览




文档简介
7~8章 阶段练(1)(基础)【平面图形的认识(二)、幂的运算】
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、下列计算正确的是( )
A.a4÷a3=1 B.a4+a3=a7 C.a4 a3=a7 D.(2a3)4=8a12
2、(2020春 姜堰区期中)已知三角形的两边长分别为1和4,且第三边长为整数,则第三边长为( )
A.3 B.4 C.5 D.6
3、将数5.01×10﹣5用小数表示,正确的是( )
A.0.0000501 B.0.00000501 C.0.000501 D.﹣0.0000501
4、将()﹣1,(﹣3)0,(﹣2)3这三个数按从小到大的顺序排列,正确的顺序是( )
A.()﹣1<(﹣3)0<(﹣2)3 B.(﹣3)0<(﹣2)3<()﹣1
C.(﹣2)3<()﹣1<(﹣3)0 D.(﹣2)3<(﹣3)0<()﹣1
5、(2020春 赣榆区期中)如图,下列条件中不能判断a∥b的是( )
A.∠1=∠2 B.∠3+∠4=90° C.∠2=∠3 D.∠3=∠4
(5题) (6题)
6、如图,一条公路经过两次转弯后又回到原来的方向,如果第一次的拐角为150°,则第二次的拐角为( )
A.40° B.50° C.140° D.150°
7、(2020春 江阴市期中)如图,AB∥CD,直线l分别交AB、CD于E、F,∠1=58°,则∠2的度数是( )
A.58° B.148° C.132° D.122°
8、(2020秋 武进区期中)正九边形的每个内角的度数为( )
A.40° B.80° C.120° D.140°
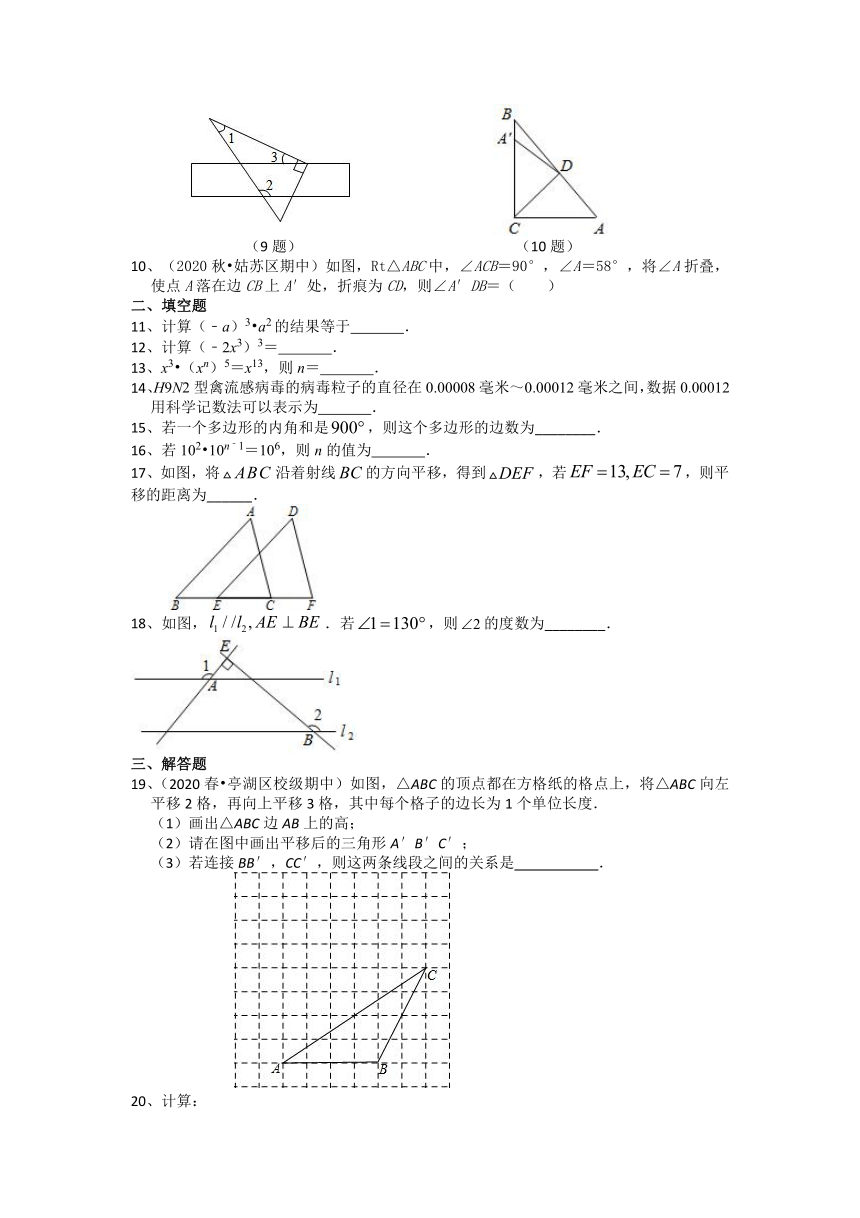
9、(2020春 常州期中)如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=125°,则∠3等于( )
A.45° B.35° C.25° D.15°
(9题) (10题)
10、(2020秋 姑苏区期中)如图,Rt△ABC中,∠ACB=90°,∠A=58°,将∠A折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
二、填空题
11、计算(﹣a)3 a2的结果等于 .
12、计算(﹣2x3)3= .
13、x3 (xn)5=x13,则n= .
14、H9N2型禽流感病毒的病毒粒子的直径在0.00008毫米~0.00012毫米之间,数据0.00012用科学记数法可以表示为 .
15、若一个多边形的内角和是,则这个多边形的边数为________.
16、若102 10n﹣1=106,则n的值为 .
17、如图,将沿着射线的方向平移,得到,若,则平移的距离为______.
18、如图,.若,则的度数为________.
三、解答题
19、(2020春 亭湖区校级期中)如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移2格,再向上平移3格,其中每个格子的边长为1个单位长度.
(1)画出△ABC边AB上的高;
(2)请在图中画出平移后的三角形A′B′C′;
(3)若连接BB′,CC′,则这两条线段之间的关系是 .
20、计算:
(1) ( ) ·() (2) ( -)÷(-)·(-)
(3)()÷()·()(≠0) (4) (-2)-(-)·(-2)
(5)(-1)+2-()+(π-3.14) (6) (-0.125) ×(-1)×(-8) ×(-)
21、(1)已知m+4n﹣3=0,求2m 16n的值.
(2)已知n为正整数,且x2n=4,求(x3n)2﹣2(x2)2n的值.
22、如图,已知DE∥AF,∠CDA=∠DAB.求证:∠1=∠2.
23、如图:已知AC∥DE,DC∥EF,CD平分∠BCA.求证:EF平分∠BED.
24、如图,BD是△ABC的角平分线,ED∥BC,交AB于点E.
(1)若∠A=44°,∠BDC=60°,求∠BED的度数;
(2)若∠A﹣∠ABD=31°,∠EDC=76°,求∠ADB的度数.
25、(2021春 靖江市月考)如图①,中,平分,且与的外角的角平分线交于点.
(1)若,,求的度数;
(2)若把截去,得到四边形,如图②,猜想、、的关系,并说明理由.
26、如图,直线HD∥GE,点A在直线HD上,点C在直线GE上,点B在直线HD、GE之间,∠DAB=120°.
(1)如图1,若∠BCG=40°,求∠ABC的度数;
(2)如图2,AF平分∠HAB,BC平分∠FCG,∠BCG=20°,比较∠B,∠F的大小;
(3)如图3,点P是线段AB上一点,PN平分∠APC,CN平分∠PCE,探究∠HAP和∠N的数量关系,并说明理由.
7~8章 阶段练(1)(基础)【平面图形的认识(二)、幂的运算】
-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、下列计算正确的是( )
A.a4÷a3=1 B.a4+a3=a7 C.a4 a3=a7 D.(2a3)4=8a12
解:A、a4÷a3=a,故此选项错误;
B、a4+a3,无法合并,故此选项错误;
C、a4 a3=a7,正确;
D、(2a3)4=16a12,故此选项错误.
故选:C.
2、(2020春 姜堰区期中)已知三角形的两边长分别为1和4,且第三边长为整数,则第三边长为( )
A.3 B.4 C.5 D.6
解:根据三角形的三边关系,得
4﹣1<第三边长<4+1,即3<第三边长<5,
又第三条边长为整数,
则第三边长为4.
故选:B.
3、将数5.01×10﹣5用小数表示,正确的是( )
A.0.0000501 B.0.00000501 C.0.000501 D.﹣0.0000501
解:将数5.01×10﹣5用小数表示,正确的是0.0000501.
故选:A.
4、将()﹣1,(﹣3)0,(﹣2)3这三个数按从小到大的顺序排列,正确的顺序是( )
A.()﹣1<(﹣3)0<(﹣2)3 B.(﹣3)0<(﹣2)3<()﹣1
C.(﹣2)3<()﹣1<(﹣3)0 D.(﹣2)3<(﹣3)0<()﹣1
解:∵()﹣1=4,(﹣3)0=1,(﹣2)3=﹣8,
∴(﹣2)3<(﹣3)0<()﹣1.
故选:D.
5、(2020春 赣榆区期中)如图,下列条件中不能判断a∥b的是( )
A.∠1=∠2 B.∠3+∠4=90° C.∠2=∠3 D.∠3=∠4
解:A、∠1=∠2可以判定a,b平行,不符合题意;
B、∠3+∠4=90°,∠3+∠4+90°=180°,可以判定a,b平行,不符合题意;
C、∠2=∠3可以判定a,b平行,不符合题意;
D、∠3=∠4不能判断直线a、b平行,符合题意.
故选:D.
6、如图,一条公路经过两次转弯后又回到原来的方向,如果第一次的拐角为150°,则第二次的拐角为( )
A.40° B.50° C.140° D.150°
【分析】直接根据平行线的性质即可得出结论.
解:∵AB∥CD,∠B=150°,
∴∠C=∠B=150°.
故选:D.
7、(2020春 江阴市期中)如图,AB∥CD,直线l分别交AB、CD于E、F,∠1=58°,则∠2的度数是( )
A.58° B.148° C.132° D.122°
解:∵AB∥CD,
∴∠CFE=∠1=58°,
∴∠2=180°﹣58°=122°,
故选:D.
8、(2020秋 武进区期中)正九边形的每个内角的度数为( )
A.40° B.80° C.120° D.140°
解:(9﹣2)×180°÷9=140°,
故选:D.
9、(2020春 常州期中)如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=125°,则∠3等于( )
A.45° B.35° C.25° D.15°
解:如下图所示,
∵AB∥CD,
∴∠4+∠2=180°(两直线平行,同旁内角互补),
∴∠4=180°﹣∠2=180°﹣125°=55°,
∴∠3=∠4﹣∠1=55°﹣30°=25°,
故选:C.
10、(2020秋 姑苏区期中)如图,Rt△ABC中,∠ACB=90°,∠A=58°,将∠A折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
A.16° B.20° C.26° D.28°
解:∵∠ACB=90°,∠A=58°,
∴∠B=90°﹣∠A=32°,
由翻折的性质可知,∠CA′D=∠A=58°,
∵∠CA′D=′B+′A′DB,
∴∠A′DB=58°﹣32°=26°,
故选:C.
二、填空题
11、计算(﹣a)3 a2的结果等于 .
解:(﹣a)3 a2=﹣a3 a2=﹣a5,
故答案为:﹣a5.
12、计算(﹣2x3)3= .
解:(﹣2x3)3=﹣8x9,
故答案为:﹣8x9.
13、x3 (xn)5=x13,则n= .
解:∵x3 (xn)5=x13,
∴3+5n=13,
解得:n=2.
故答案为:2.
14、H9N2型禽流感病毒的病毒粒子的直径在0.00008毫米~0.00012毫米之间,数据0.00012用科学记数法可以表示为 .
解:数据0.00012用科学记数法可以表示为1.2×10﹣4.
故答案为:1.2×10﹣4.
15、若一个多边形的内角和是,则这个多边形的边数为________.
【答案】七
【分析】
根据多边形的内角和公式(n-2) 180°,列式求解即可.
【详解】
解:设这个多边形是n边形,根据题意得,
(n-2) 180°=900°,
解得n=7.
故答案为:七.
16、若102 10n﹣1=106,则n的值为 .
解:∵102 10n﹣1=106,
∴102+n﹣1=106,
∴2+n﹣1=6,
解得n=5,
故答案为:5.
17、如图,将沿着射线的方向平移,得到,若,则平移的距离为______.
【答案】6
【分析】
根据平移的性质,结合图形与已知条件可直接求得结果.
【详解】
解:根据图形可得:线段CF的长度即为平移的距离,
∵EF=13,EC=7,
∴CF=EF EC=13 7=6.
故答案为:6.
18、如图,.若,则的度数为________.
【答案】
【分析】
根据平角的定义得出,由三角形外角的性质得出,根据平行线的性质得出即可.
【详解】
解:如图,
∵,∴,
∵.∴,
∵,∴.
故答案为:.
三、解答题
19、(2020春 亭湖区校级期中)如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移2格,再向上平移3格,其中每个格子的边长为1个单位长度.
(1)画出△ABC边AB上的高;
(2)请在图中画出平移后的三角形A′B′C′;
(3)若连接BB′,CC′,则这两条线段之间的关系是 .
【分析】(1)依据三角形高线的概念即可得到△ABC边AB上的高;
(2)依据平移的方向和距离,即可得到平移后的三角形A′B′C′;
(3)依据平移的性质,即可得到BB′,CC′这两条线段之间的关系是平行且相等.
【解析】(1)如图所示,CD即为△ABC的边AB上的高;
(2)如图所示,△A'B'C'即为所求;
(3)若连接BB′,CC′,则这两条线段之间的关系是平行且相等.
故答案为:平行且相等.
20、计算:
(1) ( ) ·() (2) ( -)÷(-)·(-)
(3)()÷()·()(≠0) (4) (-2)-(-)·(-2)
(5)(-1)+2-()+(π-3.14) (6) (-0.125) ×(-1)×(-8) ×(-)
解:(1)原式= ·(-)=-
(2)原式=
(3)原式=÷·==
(4)原式==-28
(5)原式=-1+-+1=
(6)原式=()×[-()]×[-8]×()
=(×8)×8×(×)×=
21、(1)已知m+4n﹣3=0,求2m 16n的值.
(2)已知n为正整数,且x2n=4,求(x3n)2﹣2(x2)2n的值.
解:(1)∵m+4n﹣3=0
∴m+4n=3
原式=2m 24n
=2m+4n
=23
=8.
(2)原式=(x2n)3﹣2(x2n)2,
=43﹣2×42,
=32,
22、如图,已知DE∥AF,∠CDA=∠DAB.求证:∠1=∠2.
证明:∵DE∥AF,
∴∠EDA=∠DAF,
∵∠CDA=∠DAB,
∴∠CDA﹣∠EDA=∠DAB﹣∠DAF,
∴∠1=∠2.
23、如图:已知AC∥DE,DC∥EF,CD平分∠BCA.求证:EF平分∠BED.
证明:
∵AC∥DE,∴∠3=∠5,
∵DC∥EF,∴∠2=∠3,∠1=∠4,∴∠2=∠5,
∵CD平分∠BCA,∴∠4=∠5,∴∠1=∠5,
∴∠1=∠2,∴EF平分∠BED.
24、如图,BD是△ABC的角平分线,ED∥BC,交AB于点E.
(1)若∠A=44°,∠BDC=60°,求∠BED的度数;
(2)若∠A﹣∠ABD=31°,∠EDC=76°,求∠ADB的度数.
解:如图,∵∠BDC=60°,∴∠ADB=120°.
又∵∠A=44°,∴∠2=180°﹣44°﹣120°=16°.
∵BD是△ABC的角平分线,∴∠1=∠2=16°.
又ED∥BC,∴∠BED+2∠1=180°,
∴∠BED=180°﹣32°=148°;
(2)∵ED∥BC,∴∠EDC+∠C=180°.
又∵∠EDC=76°,∴∠C=104°.
BD是△ABC的角平分线,∴∠1=∠2.
∵∠A﹣∠2=31°,∠A+2∠2+∠C=180°∴∠1=∠2=15°,
∴∠ADB=∠1+∠C=119°.
25、(2021春 靖江市月考)如图①,中,平分,且与的外角的角平分线交于点.
(1)若,,求的度数;
(2)若把截去,得到四边形,如图②,猜想、、的关系,并说明理由.
【分析】(1)根据三角形内角和定理以及角平分线性质,先求出、的等式,推出,最后代入求出即可;
(2)根据(1)中的结论即可得到结论.
【解析】(1),
,,
又平分,平分,,,
,,,
,,
,;
(2);
理由:延长、交于点,
,,,
,
则,
由(1)知,,
.
26、如图,直线HD∥GE,点A在直线HD上,点C在直线GE上,点B在直线HD、GE之间,∠DAB=120°.
(1)如图1,若∠BCG=40°,求∠ABC的度数;
(2)如图2,AF平分∠HAB,BC平分∠FCG,∠BCG=20°,比较∠B,∠F的大小;
(3)如图3,点P是线段AB上一点,PN平分∠APC,CN平分∠PCE,探究∠HAP和∠N的数量关系,并说明理由.
解:(1)过点B作BM∥HD,则HD∥GE∥BM,如图1,
∴∠ABM=180°﹣∠DAB,∠CBM=∠BCG,
∵∠DAB=120°,∠BCG=40°,
∴∠ABM=60°,∠CBM=40°,∴∠ABC=∠ABM+∠CBM=100°;
(2)过B作BP∥HD∥GH,过F作FQ∥HD∥GH,如图2,
∴∠ABP=∠HAB,∠CBP=∠BCG,∠AFQ=∠HAF,∠CFQ=∠FCG,
∴∠ABC=∠HAB+∠BCG,∠AFC=∠HAF+∠FCG,
∵∠DAB=120°,∴∠HAB=180°﹣120°=60°,
∵AF平分∠HAB,BC平分∠FCG,∠BCG=20°,∴∠HAF=30°,∠FCG=40°,
∴∠ABC=60°+20°=80°,∠AFC=30°+40°=70°,∴∠ABC>∠AFC;
(3)过P作PK∥HD∥GE,如图3,∴∠APK=∠HAP,∠CPK=∠PCG,
∴∠APC=∠HAP+∠PCG,
∵PN平分∠APC,∴∠NPC=∠HAP+∠PCG,
∵∠PCE=180°﹣∠PCG,CN平分∠PCE,∴∠PCN==90°﹣∠PCG,
∵∠N+∠NPC+∠PCN=180°,
∴∠N=180°﹣∠HAP﹣∠PCG﹣90°+∠PCG=90°﹣∠HAP,
即,∠N=90°﹣∠HAP.
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、下列计算正确的是( )
A.a4÷a3=1 B.a4+a3=a7 C.a4 a3=a7 D.(2a3)4=8a12
2、(2020春 姜堰区期中)已知三角形的两边长分别为1和4,且第三边长为整数,则第三边长为( )
A.3 B.4 C.5 D.6
3、将数5.01×10﹣5用小数表示,正确的是( )
A.0.0000501 B.0.00000501 C.0.000501 D.﹣0.0000501
4、将()﹣1,(﹣3)0,(﹣2)3这三个数按从小到大的顺序排列,正确的顺序是( )
A.()﹣1<(﹣3)0<(﹣2)3 B.(﹣3)0<(﹣2)3<()﹣1
C.(﹣2)3<()﹣1<(﹣3)0 D.(﹣2)3<(﹣3)0<()﹣1
5、(2020春 赣榆区期中)如图,下列条件中不能判断a∥b的是( )
A.∠1=∠2 B.∠3+∠4=90° C.∠2=∠3 D.∠3=∠4
(5题) (6题)
6、如图,一条公路经过两次转弯后又回到原来的方向,如果第一次的拐角为150°,则第二次的拐角为( )
A.40° B.50° C.140° D.150°
7、(2020春 江阴市期中)如图,AB∥CD,直线l分别交AB、CD于E、F,∠1=58°,则∠2的度数是( )
A.58° B.148° C.132° D.122°
8、(2020秋 武进区期中)正九边形的每个内角的度数为( )
A.40° B.80° C.120° D.140°
9、(2020春 常州期中)如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=125°,则∠3等于( )
A.45° B.35° C.25° D.15°
(9题) (10题)
10、(2020秋 姑苏区期中)如图,Rt△ABC中,∠ACB=90°,∠A=58°,将∠A折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
二、填空题
11、计算(﹣a)3 a2的结果等于 .
12、计算(﹣2x3)3= .
13、x3 (xn)5=x13,则n= .
14、H9N2型禽流感病毒的病毒粒子的直径在0.00008毫米~0.00012毫米之间,数据0.00012用科学记数法可以表示为 .
15、若一个多边形的内角和是,则这个多边形的边数为________.
16、若102 10n﹣1=106,则n的值为 .
17、如图,将沿着射线的方向平移,得到,若,则平移的距离为______.
18、如图,.若,则的度数为________.
三、解答题
19、(2020春 亭湖区校级期中)如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移2格,再向上平移3格,其中每个格子的边长为1个单位长度.
(1)画出△ABC边AB上的高;
(2)请在图中画出平移后的三角形A′B′C′;
(3)若连接BB′,CC′,则这两条线段之间的关系是 .
20、计算:
(1) ( ) ·() (2) ( -)÷(-)·(-)
(3)()÷()·()(≠0) (4) (-2)-(-)·(-2)
(5)(-1)+2-()+(π-3.14) (6) (-0.125) ×(-1)×(-8) ×(-)
21、(1)已知m+4n﹣3=0,求2m 16n的值.
(2)已知n为正整数,且x2n=4,求(x3n)2﹣2(x2)2n的值.
22、如图,已知DE∥AF,∠CDA=∠DAB.求证:∠1=∠2.
23、如图:已知AC∥DE,DC∥EF,CD平分∠BCA.求证:EF平分∠BED.
24、如图,BD是△ABC的角平分线,ED∥BC,交AB于点E.
(1)若∠A=44°,∠BDC=60°,求∠BED的度数;
(2)若∠A﹣∠ABD=31°,∠EDC=76°,求∠ADB的度数.
25、(2021春 靖江市月考)如图①,中,平分,且与的外角的角平分线交于点.
(1)若,,求的度数;
(2)若把截去,得到四边形,如图②,猜想、、的关系,并说明理由.
26、如图,直线HD∥GE,点A在直线HD上,点C在直线GE上,点B在直线HD、GE之间,∠DAB=120°.
(1)如图1,若∠BCG=40°,求∠ABC的度数;
(2)如图2,AF平分∠HAB,BC平分∠FCG,∠BCG=20°,比较∠B,∠F的大小;
(3)如图3,点P是线段AB上一点,PN平分∠APC,CN平分∠PCE,探究∠HAP和∠N的数量关系,并说明理由.
7~8章 阶段练(1)(基础)【平面图形的认识(二)、幂的运算】
-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、下列计算正确的是( )
A.a4÷a3=1 B.a4+a3=a7 C.a4 a3=a7 D.(2a3)4=8a12
解:A、a4÷a3=a,故此选项错误;
B、a4+a3,无法合并,故此选项错误;
C、a4 a3=a7,正确;
D、(2a3)4=16a12,故此选项错误.
故选:C.
2、(2020春 姜堰区期中)已知三角形的两边长分别为1和4,且第三边长为整数,则第三边长为( )
A.3 B.4 C.5 D.6
解:根据三角形的三边关系,得
4﹣1<第三边长<4+1,即3<第三边长<5,
又第三条边长为整数,
则第三边长为4.
故选:B.
3、将数5.01×10﹣5用小数表示,正确的是( )
A.0.0000501 B.0.00000501 C.0.000501 D.﹣0.0000501
解:将数5.01×10﹣5用小数表示,正确的是0.0000501.
故选:A.
4、将()﹣1,(﹣3)0,(﹣2)3这三个数按从小到大的顺序排列,正确的顺序是( )
A.()﹣1<(﹣3)0<(﹣2)3 B.(﹣3)0<(﹣2)3<()﹣1
C.(﹣2)3<()﹣1<(﹣3)0 D.(﹣2)3<(﹣3)0<()﹣1
解:∵()﹣1=4,(﹣3)0=1,(﹣2)3=﹣8,
∴(﹣2)3<(﹣3)0<()﹣1.
故选:D.
5、(2020春 赣榆区期中)如图,下列条件中不能判断a∥b的是( )
A.∠1=∠2 B.∠3+∠4=90° C.∠2=∠3 D.∠3=∠4
解:A、∠1=∠2可以判定a,b平行,不符合题意;
B、∠3+∠4=90°,∠3+∠4+90°=180°,可以判定a,b平行,不符合题意;
C、∠2=∠3可以判定a,b平行,不符合题意;
D、∠3=∠4不能判断直线a、b平行,符合题意.
故选:D.
6、如图,一条公路经过两次转弯后又回到原来的方向,如果第一次的拐角为150°,则第二次的拐角为( )
A.40° B.50° C.140° D.150°
【分析】直接根据平行线的性质即可得出结论.
解:∵AB∥CD,∠B=150°,
∴∠C=∠B=150°.
故选:D.
7、(2020春 江阴市期中)如图,AB∥CD,直线l分别交AB、CD于E、F,∠1=58°,则∠2的度数是( )
A.58° B.148° C.132° D.122°
解:∵AB∥CD,
∴∠CFE=∠1=58°,
∴∠2=180°﹣58°=122°,
故选:D.
8、(2020秋 武进区期中)正九边形的每个内角的度数为( )
A.40° B.80° C.120° D.140°
解:(9﹣2)×180°÷9=140°,
故选:D.
9、(2020春 常州期中)如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=125°,则∠3等于( )
A.45° B.35° C.25° D.15°
解:如下图所示,
∵AB∥CD,
∴∠4+∠2=180°(两直线平行,同旁内角互补),
∴∠4=180°﹣∠2=180°﹣125°=55°,
∴∠3=∠4﹣∠1=55°﹣30°=25°,
故选:C.
10、(2020秋 姑苏区期中)如图,Rt△ABC中,∠ACB=90°,∠A=58°,将∠A折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
A.16° B.20° C.26° D.28°
解:∵∠ACB=90°,∠A=58°,
∴∠B=90°﹣∠A=32°,
由翻折的性质可知,∠CA′D=∠A=58°,
∵∠CA′D=′B+′A′DB,
∴∠A′DB=58°﹣32°=26°,
故选:C.
二、填空题
11、计算(﹣a)3 a2的结果等于 .
解:(﹣a)3 a2=﹣a3 a2=﹣a5,
故答案为:﹣a5.
12、计算(﹣2x3)3= .
解:(﹣2x3)3=﹣8x9,
故答案为:﹣8x9.
13、x3 (xn)5=x13,则n= .
解:∵x3 (xn)5=x13,
∴3+5n=13,
解得:n=2.
故答案为:2.
14、H9N2型禽流感病毒的病毒粒子的直径在0.00008毫米~0.00012毫米之间,数据0.00012用科学记数法可以表示为 .
解:数据0.00012用科学记数法可以表示为1.2×10﹣4.
故答案为:1.2×10﹣4.
15、若一个多边形的内角和是,则这个多边形的边数为________.
【答案】七
【分析】
根据多边形的内角和公式(n-2) 180°,列式求解即可.
【详解】
解:设这个多边形是n边形,根据题意得,
(n-2) 180°=900°,
解得n=7.
故答案为:七.
16、若102 10n﹣1=106,则n的值为 .
解:∵102 10n﹣1=106,
∴102+n﹣1=106,
∴2+n﹣1=6,
解得n=5,
故答案为:5.
17、如图,将沿着射线的方向平移,得到,若,则平移的距离为______.
【答案】6
【分析】
根据平移的性质,结合图形与已知条件可直接求得结果.
【详解】
解:根据图形可得:线段CF的长度即为平移的距离,
∵EF=13,EC=7,
∴CF=EF EC=13 7=6.
故答案为:6.
18、如图,.若,则的度数为________.
【答案】
【分析】
根据平角的定义得出,由三角形外角的性质得出,根据平行线的性质得出即可.
【详解】
解:如图,
∵,∴,
∵.∴,
∵,∴.
故答案为:.
三、解答题
19、(2020春 亭湖区校级期中)如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移2格,再向上平移3格,其中每个格子的边长为1个单位长度.
(1)画出△ABC边AB上的高;
(2)请在图中画出平移后的三角形A′B′C′;
(3)若连接BB′,CC′,则这两条线段之间的关系是 .
【分析】(1)依据三角形高线的概念即可得到△ABC边AB上的高;
(2)依据平移的方向和距离,即可得到平移后的三角形A′B′C′;
(3)依据平移的性质,即可得到BB′,CC′这两条线段之间的关系是平行且相等.
【解析】(1)如图所示,CD即为△ABC的边AB上的高;
(2)如图所示,△A'B'C'即为所求;
(3)若连接BB′,CC′,则这两条线段之间的关系是平行且相等.
故答案为:平行且相等.
20、计算:
(1) ( ) ·() (2) ( -)÷(-)·(-)
(3)()÷()·()(≠0) (4) (-2)-(-)·(-2)
(5)(-1)+2-()+(π-3.14) (6) (-0.125) ×(-1)×(-8) ×(-)
解:(1)原式= ·(-)=-
(2)原式=
(3)原式=÷·==
(4)原式==-28
(5)原式=-1+-+1=
(6)原式=()×[-()]×[-8]×()
=(×8)×8×(×)×=
21、(1)已知m+4n﹣3=0,求2m 16n的值.
(2)已知n为正整数,且x2n=4,求(x3n)2﹣2(x2)2n的值.
解:(1)∵m+4n﹣3=0
∴m+4n=3
原式=2m 24n
=2m+4n
=23
=8.
(2)原式=(x2n)3﹣2(x2n)2,
=43﹣2×42,
=32,
22、如图,已知DE∥AF,∠CDA=∠DAB.求证:∠1=∠2.
证明:∵DE∥AF,
∴∠EDA=∠DAF,
∵∠CDA=∠DAB,
∴∠CDA﹣∠EDA=∠DAB﹣∠DAF,
∴∠1=∠2.
23、如图:已知AC∥DE,DC∥EF,CD平分∠BCA.求证:EF平分∠BED.
证明:
∵AC∥DE,∴∠3=∠5,
∵DC∥EF,∴∠2=∠3,∠1=∠4,∴∠2=∠5,
∵CD平分∠BCA,∴∠4=∠5,∴∠1=∠5,
∴∠1=∠2,∴EF平分∠BED.
24、如图,BD是△ABC的角平分线,ED∥BC,交AB于点E.
(1)若∠A=44°,∠BDC=60°,求∠BED的度数;
(2)若∠A﹣∠ABD=31°,∠EDC=76°,求∠ADB的度数.
解:如图,∵∠BDC=60°,∴∠ADB=120°.
又∵∠A=44°,∴∠2=180°﹣44°﹣120°=16°.
∵BD是△ABC的角平分线,∴∠1=∠2=16°.
又ED∥BC,∴∠BED+2∠1=180°,
∴∠BED=180°﹣32°=148°;
(2)∵ED∥BC,∴∠EDC+∠C=180°.
又∵∠EDC=76°,∴∠C=104°.
BD是△ABC的角平分线,∴∠1=∠2.
∵∠A﹣∠2=31°,∠A+2∠2+∠C=180°∴∠1=∠2=15°,
∴∠ADB=∠1+∠C=119°.
25、(2021春 靖江市月考)如图①,中,平分,且与的外角的角平分线交于点.
(1)若,,求的度数;
(2)若把截去,得到四边形,如图②,猜想、、的关系,并说明理由.
【分析】(1)根据三角形内角和定理以及角平分线性质,先求出、的等式,推出,最后代入求出即可;
(2)根据(1)中的结论即可得到结论.
【解析】(1),
,,
又平分,平分,,,
,,,
,,
,;
(2);
理由:延长、交于点,
,,,
,
则,
由(1)知,,
.
26、如图,直线HD∥GE,点A在直线HD上,点C在直线GE上,点B在直线HD、GE之间,∠DAB=120°.
(1)如图1,若∠BCG=40°,求∠ABC的度数;
(2)如图2,AF平分∠HAB,BC平分∠FCG,∠BCG=20°,比较∠B,∠F的大小;
(3)如图3,点P是线段AB上一点,PN平分∠APC,CN平分∠PCE,探究∠HAP和∠N的数量关系,并说明理由.
解:(1)过点B作BM∥HD,则HD∥GE∥BM,如图1,
∴∠ABM=180°﹣∠DAB,∠CBM=∠BCG,
∵∠DAB=120°,∠BCG=40°,
∴∠ABM=60°,∠CBM=40°,∴∠ABC=∠ABM+∠CBM=100°;
(2)过B作BP∥HD∥GH,过F作FQ∥HD∥GH,如图2,
∴∠ABP=∠HAB,∠CBP=∠BCG,∠AFQ=∠HAF,∠CFQ=∠FCG,
∴∠ABC=∠HAB+∠BCG,∠AFC=∠HAF+∠FCG,
∵∠DAB=120°,∴∠HAB=180°﹣120°=60°,
∵AF平分∠HAB,BC平分∠FCG,∠BCG=20°,∴∠HAF=30°,∠FCG=40°,
∴∠ABC=60°+20°=80°,∠AFC=30°+40°=70°,∴∠ABC>∠AFC;
(3)过P作PK∥HD∥GE,如图3,∴∠APK=∠HAP,∠CPK=∠PCG,
∴∠APC=∠HAP+∠PCG,
∵PN平分∠APC,∴∠NPC=∠HAP+∠PCG,
∵∠PCE=180°﹣∠PCG,CN平分∠PCE,∴∠PCN==90°﹣∠PCG,
∵∠N+∠NPC+∠PCN=180°,
∴∠N=180°﹣∠HAP﹣∠PCG﹣90°+∠PCG=90°﹣∠HAP,
即,∠N=90°﹣∠HAP.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
