2021-2022学年苏科版七年级数学下册7~8章阶段练(2)(基础)(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册7~8章阶段练(2)(基础)(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 793.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-10 00:00:00 | ||
图片预览


文档简介
7~8章 阶段练(2)(基础)【平面图形的认识(二)、幂的运算】
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、(2020春 广陵区校级期中)下列车标,可看作图案的某一部分经过平移所形成的是( )
A.B.C.D.
2、下列运算正确的是( )
A.4a3﹣a3=3a3 B.a4 a4=a16 C.(3a)2=6a2 D.a6÷a2=a3
3、(2020春 江阴市期中)已知三角形的三边长分别为2、x、3,则x可能是( )
A.5 B.1 C.6 D.4
4、(2020春 南京期中)计算:( 3)2=2 (3)2=2 6=8,其中,第一步运算的依据是( )
A.同底数幂的乘法法则 B.幂的乘方法则
C.乘法分配律 D.积的乘方法则
5、(﹣0.125)2018×82019等于( )
A.﹣8 B.8 C.0.125 D.﹣0.125
6、若(ambn)3=a9b15,则m、n的值分别为( )
A.9;5 B.3;5 C.5;3 D.6;12
7、(2020春 仪征市期中)如图,∠1=80°,要使得m∥n,则∠2的度数是( )
A.120° B.110° C.100° D.80°
8、(2020春 江阴市期中)如图,在下列给出的条件中,不能判定AB∥DF的是( )
A.∠A=∠3 B.∠A+∠2=180° C.∠1=∠4 D.∠1=∠A
9、(2020秋 苏州期中)将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形(△ABC),BC为折痕,若∠1=42°,则∠2的度数为( )
A.48° B.58° C.60° D.69°
10、(2020春 江阴市期中)如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=68°,则∠AED的度数是( )
A.88° B.98° C.92° D.112°
二、填空题
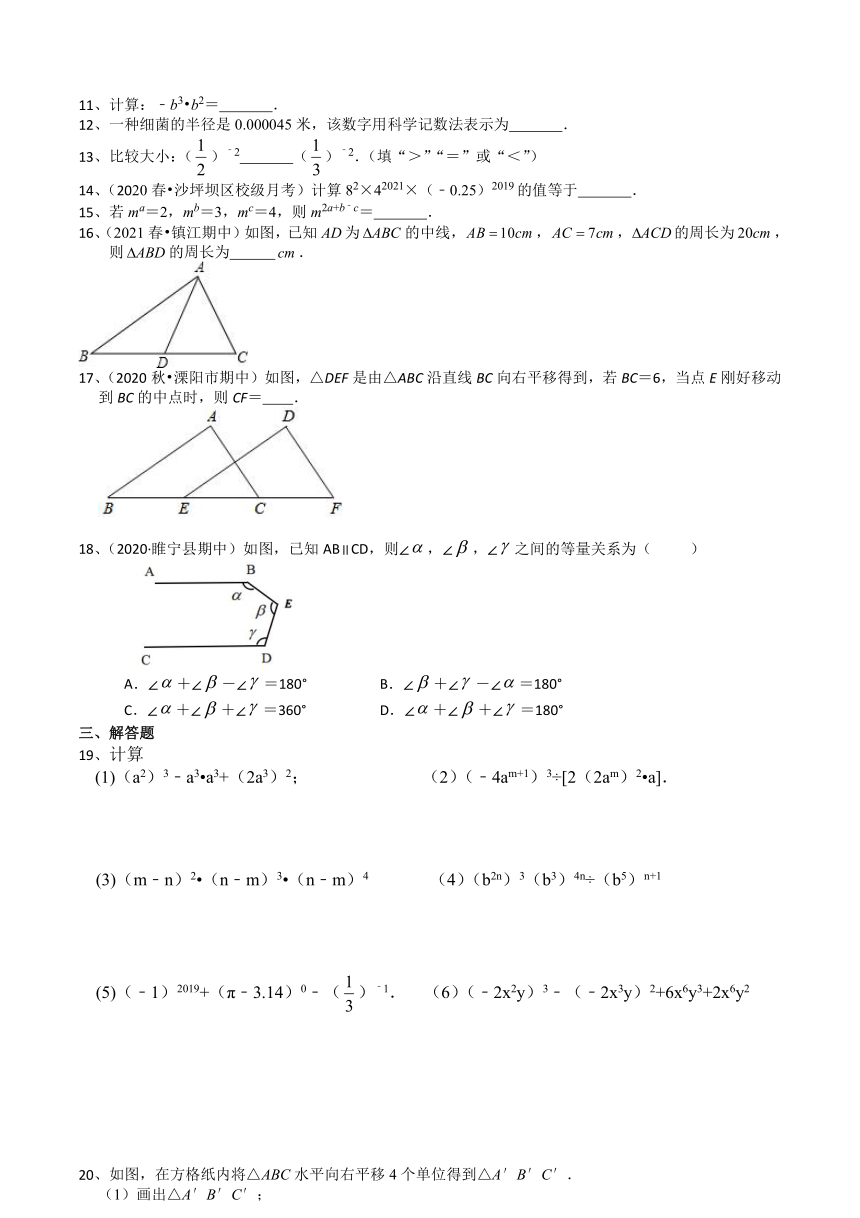
11、计算:﹣b3 b2= .
12、一种细菌的半径是0.000045米,该数字用科学记数法表示为 .
13、比较大小:()﹣2 ()﹣2.(填“>”“=”或“<”)
14、(2020春 沙坪坝区校级月考)计算82×42021×(﹣0.25)2019的值等于 .
15、若ma=2,mb=3,mc=4,则m2a+b﹣c= .
16、(2021春 镇江期中)如图,已知为的中线,,,的周长为,则的周长为 .
17、(2020秋 溧阳市期中)如图,△DEF是由△ABC沿直线BC向右平移得到,若BC=6,当点E刚好移动到BC的中点时,则CF= .
18、(2020·睢宁县期中)如图,已知AB∥CD,则∠,∠,∠之间的等量关系为( )
A.∠+∠-∠=180° B.∠+∠-∠=180°
C.∠+∠+∠=360° D.∠+∠+∠=180°
三、解答题
19、计算
(1)(a2)3﹣a3 a3+(2a3)2; (2)(﹣4am+1)3÷[2(2am)2 a].
(3)(m﹣n)2 (n﹣m)3 (n﹣m)4 (4)(b2n)3(b3)4n÷(b5)n+1
(5)(﹣1)2019+(π﹣3.14)0﹣()﹣1. (6)(﹣2x2y)3﹣(﹣2x3y)2+6x6y3+2x6y2
20、如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
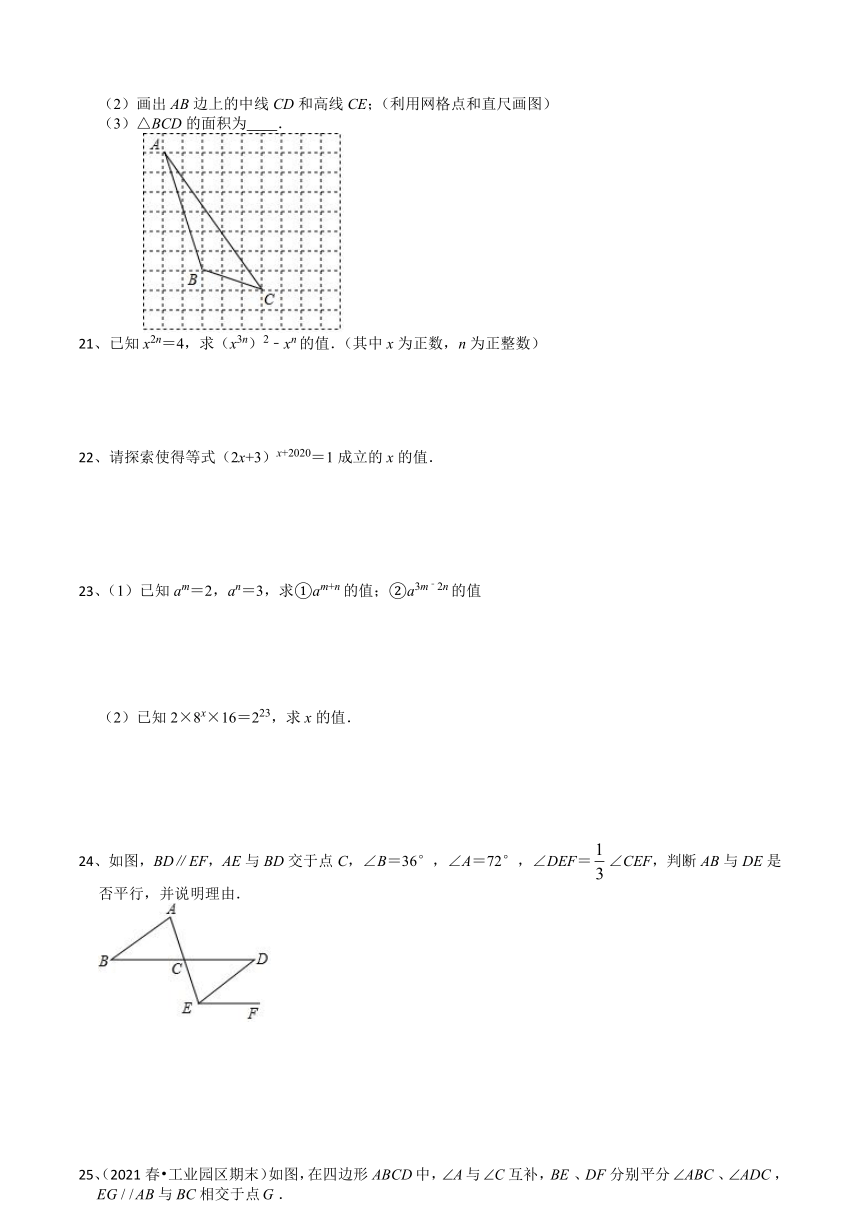
(1)画出△A′B′C′;
(2)画出AB边上的中线CD和高线CE;(利用网格点和直尺画图)
(3)△BCD的面积为 .
21、已知x2n=4,求(x3n)2﹣xn的值.(其中x为正数,n为正整数)
22、请探索使得等式(2x+3)x+2020=1成立的x的值.
23、(1)已知am=2,an=3,求①am+n的值;②a3m﹣2n的值
(2)已知2×8x×16=223,求x的值.
24、如图,BD∥EF,AE与BD交于点C,∠B=36°,∠A=72°,∠DEF=∠CEF,判断AB与DE是否平行,并说明理由.
25、(2021春 工业园区期末)如图,在四边形中,与互补,、分别平分、,与相交于点.
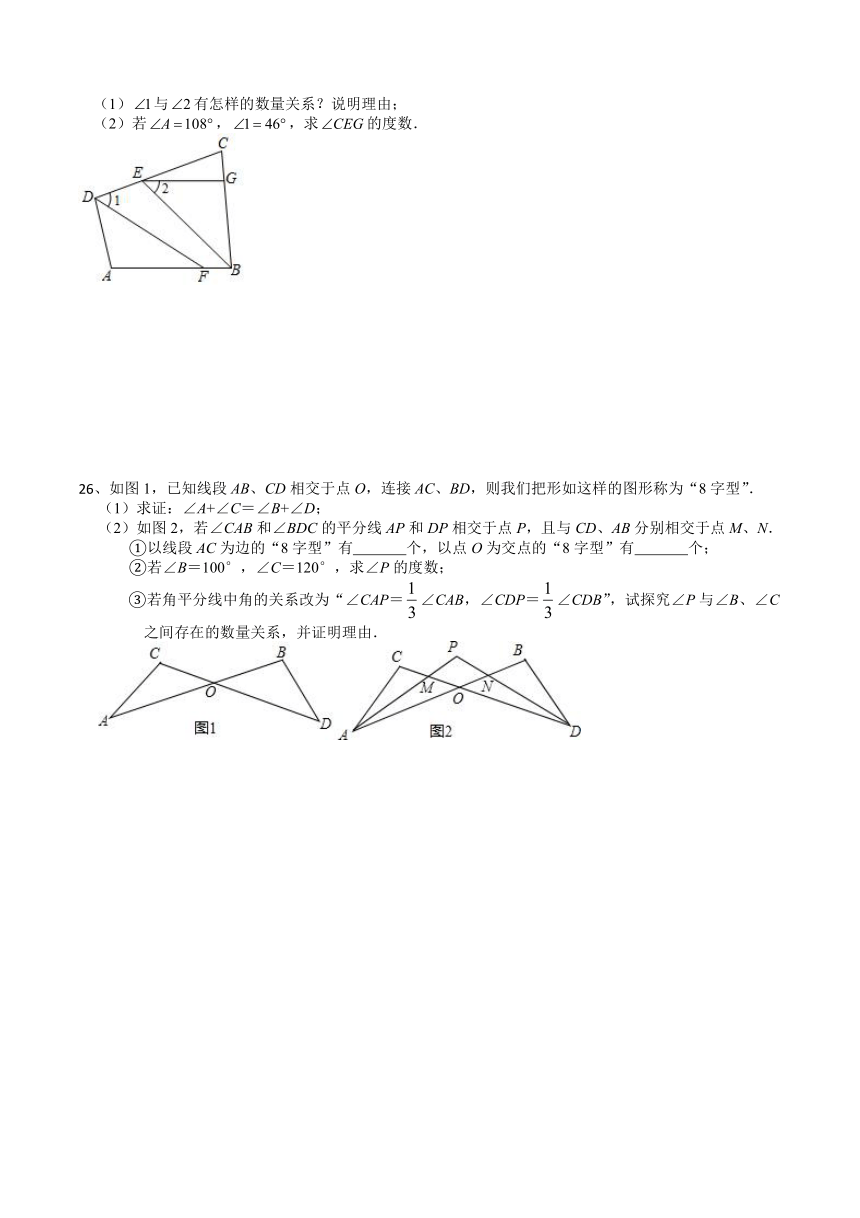
(1)与有怎样的数量关系?说明理由;
(2)若,,求的度数.
26、如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAP=∠CAB,∠CDP=∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
7~8章 阶段练(2)(基础)【平面图形的认识(二)、幂的运算】
-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、(2020春 广陵区校级期中)下列车标,可看作图案的某一部分经过平移所形成的是( )
A.B.C.D.
解:选项A,B,C不能由基本图形平移得到,选项B是由基本图形圆平移得到,
故选:D.
2、下列运算正确的是( )
A.4a3﹣a3=3a3 B.a4 a4=a16 C.(3a)2=6a2 D.a6÷a2=a3
解:A、4a3﹣a3=3a3,故选项正确;
B、a4×a4=a8,故选项错误;
C(3a)2=9a2,故选项错误;
D、a6÷a2=a4,故选项错误;
故选:A.
3、(2020春 江阴市期中)已知三角形的三边长分别为2、x、3,则x可能是( )
A.5 B.1 C.6 D.4
解:∵2+3=5,3﹣2=1,
∴1<x<5.
故选:D.
4、(2020春 南京期中)计算:( 3)2=2 (3)2=2 6=8,其中,第一步运算的依据是( )
A.同底数幂的乘法法则 B.幂的乘方法则
C.乘法分配律 D.积的乘方法则
解:计算:(a a3)2=a2 (a3)2=a2 a6=a8,其中,第一步运算的依据是积的乘方法则.
故选:D.
5、(﹣0.125)2018×82019等于( )
A.﹣8 B.8 C.0.125 D.﹣0.125
解:(﹣0.125)2018×82019=(﹣0.125)2018×82018×8=(﹣0.125×8)2018×8=1×8=8,
故选:B.
6、若(ambn)3=a9b15,则m、n的值分别为( )
A.9;5 B.3;5 C.5;3 D.6;12
解:∵(ambn)3=a9b15,
∴a3mb3n=a9b15,
∴3m=9,3n=15,
∴m=3,n=5,
故选:B.
7、(2020春 仪征市期中)如图,∠1=80°,要使得m∥n,则∠2的度数是( )
A.120° B.110° C.100° D.80°
解:∵∠1=80°,m∥n,
∴∠3=∠1=80°,
∴∠2=180°﹣∠3=100°.
故选:C.
8、(2020春 江阴市期中)如图,在下列给出的条件中,不能判定AB∥DF的是( )
A.∠A=∠3 B.∠A+∠2=180° C.∠1=∠4 D.∠1=∠A
解:A、因为∠A=∠3,所以AB∥DF(同位角相等,两直线平行),故本选项不符合题意.
B、因为∠A+∠2=180,所以AB∥DF(同旁内角互补,两直线平行),故本选项不符合题意.
C、因为∠1=∠4,所以AB∥DF(内错角相等,两直线平行),故本选项不符合题意.
D、因为∠1=∠A,所以AC∥DE(同位角相等,两直线平行),不能证出AB∥DF,故本选项符合题意.
故选:D.
9、(2020秋 苏州期中)将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形(△ABC),BC为折痕,若∠1=42°,则∠2的度数为( )
A.48° B.58° C.60° D.69°
解:如右图所示,
∵长方形的两条长边平行,∠1=42°,
∴∠1=∠4=42°,∠4=∠5,
∴∠5=42°,
由折叠的性质可知,∠2=∠3,
∵∠2+∠3+∠5=180°,
∴∠2=69°,
故选:D.
10、(2020春 江阴市期中)如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=68°,则∠AED的度数是( )
A.88° B.98° C.92° D.112°
解:根据多边形外角和定理得到:∠1+∠2+∠3+∠4+∠5=360°,
∴∠5=360°﹣4×68°=88°,
∴∠AED=180°﹣∠5=180°﹣88°=92°.
故选:C.
二、填空题
11、计算:﹣b3 b2= .
解:原式=﹣b3+2=﹣b5,
故答案为:﹣b5
12、一种细菌的半径是0.000045米,该数字用科学记数法表示为 .
解:0.000045米用科学记数法表示为4.5×10﹣5米.
故答案为:4.5×10﹣5米.
13、比较大小:()﹣2 ()﹣2.(填“>”“=”或“<”)
解:∵()﹣2=4、()﹣2=9,
∴()﹣2<()﹣2,
故答案为:<.
14、(2020春 沙坪坝区校级月考)计算82×42021×(﹣0.25)2019的值等于 .
【分析】根据幂的乘方与积的乘方进行计算即可.
【解答】解:原式=82×42×42019×(﹣0.25)2019
=82×42×(4×﹣0.25)2019
=82×42×(﹣1)
=﹣1024.
故答案为:﹣1024.
15、若ma=2,mb=3,mc=4,则m2a+b﹣c= .
解:∵ma=2,mb=3,mc=4,
∴m2a+b﹣c=(ma)2 mb÷mc=4×3÷4=3.
故答案为:3.
16、(2021春 镇江期中)如图,已知为的中线,,,的周长为,则的周长为 .
【分析】根据三角形中线的定义可得,再表示出和的周长的差就是、的差,然后计算即可.
【解析】是边上的中线,
,
和周长的差,
的周长为,比长,
周长为:.
故答案为23.
17、(2020秋 溧阳市期中)如图,△DEF是由△ABC沿直线BC向右平移得到,若BC=6,当点E刚好移动到BC的中点时,则CF= .
【分析】根据平移性质得出BC=EF,BE=CF,进而解答即可.
【解析】由平移的性质可得:BC=EF,BE=CF,
∵BC=6,点E刚好移动到BC的中点,
∴BE=EC=CF=3,
故答案为:3.
18、(2020·睢宁县期中)如图,已知AB∥CD,则∠,∠,∠之间的等量关系为( )
A.∠+∠-∠=180° B.∠+∠-∠=180°
C.∠+∠+∠=360° D.∠+∠+∠=180°
【答案】C
【提示】过E点作EF∥AB,则EF∥CD,利用平行线性质可得∠α+∠BEF=180°,∠γ+∠DEF=180°,
根据∠BEF+∠DEF=∠β进一步计算即可得出答案.
【详解】如图所示,过E点作EF∥AB,
∵AB∥CD,∴EF∥CD,∴∠γ+∠DEF=180°,
∵EF∥AB,∴∠α+∠BEF=180°,∴∠γ+∠DEF+∠α+∠BEF=360°,
∵∠BEF+∠DEF=∠β,∴∠α+∠β+∠γ=360°, 故选:C.
三、解答题
19、计算
(1)(a2)3﹣a3 a3+(2a3)2; (2)(﹣4am+1)3÷[2(2am)2 a].
(3)(m﹣n)2 (n﹣m)3 (n﹣m)4 (4)(b2n)3(b3)4n÷(b5)n+1
(5)(﹣1)2019+(π﹣3.14)0﹣()﹣1. (6)(﹣2x2y)3﹣(﹣2x3y)2+6x6y3+2x6y2
解:(1)(a2)3﹣a3 a3+(2a3)2 =a6﹣a6+4a6=4a6;
(2)(﹣4am+1)3÷[2(2am)2 a]=﹣64a3m+3÷8a2m+1=﹣8am+2
(3)(m﹣n)2 (n﹣m)3 (n﹣m)4 =(n﹣m)2+3+4=(n﹣m)9;
(4)(b2n)3(b3)4n÷(b5)n+1=b6n b12n÷b5n+5=b6n+12n﹣5n﹣5=b13n﹣5;
(5)原式=﹣1+1﹣3=﹣3;
(6)原式=﹣8x6y3﹣4x6y2+6x6y3+2x6y2=﹣2x6y3﹣2x6y2.
20、如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
(1)画出△A′B′C′;
(2)画出AB边上的中线CD和高线CE;(利用网格点和直尺画图)
(3)△BCD的面积为 .
【分析】(1)将三角形的三顶点分别向右平移4个单位得到对应点,再顺次连接可得;
(2)根据中线和高的定义作图可得;
(3)利用割补法求解可得.
【详解】解:(1)如图所示,△A′B′C′即为所求;
(2)如图所示,CD、CE即为所求;
(3)△BCD的面积为×4×4﹣×1×3﹣×1×3﹣1=4,
故答案为:4
21、已知x2n=4,求(x3n)2﹣xn的值.(其中x为正数,n为正整数)
解:∵x2n=4,x为正数,n为正整数,
∴xn=2,
∴(x3n)2﹣xn=(xn)6﹣xn=26﹣2=62.
22、请探索使得等式(2x+3)x+2020=1成立的x的值.
解:当x+2020=0时,∴x=﹣2020,∴2x+3=﹣4037≠0,符合题意,
当2x+3=1时,∴x=﹣1,符合题意,
当2x+3=﹣1时,∴x=﹣2,∴x+2020=2018,符合题意,
综上所述,x=﹣2或x=﹣1或x=﹣2020.
23、(1)已知am=2,an=3,求①am+n的值;②a3m﹣2n的值
(2)已知2×8x×16=223,求x的值.
解:(1)①am+n=am an=2×3=6;
②a3m﹣2n=a3m÷a2n=(am)3÷(an)2=23÷32=;
(2)∵2×8x×16=223
∴2×(23)x×24=223,
∴2×23x×24=223,
∴1+3x+4=23,
解得:x=6.
24、如图,BD∥EF,AE与BD交于点C,∠B=36°,∠A=72°,∠DEF=∠CEF,判断AB与DE是否平行,并说明理由.
解:AB与DE平行,理由如下:
∵∠B=36°,∠A=72°,∴∠ACB=∠DCE=180°﹣36°﹣72°=72°,
又∵BD∥EF,∴∠DEF=∠CDE,
又∵∠DEF=∠CEF,若设∠DEF=α,则∠CDE=α,∠CED=2α,
∴在△CED中,∠DCE+∠CDE+CED=180°,即,72°+α+2α=180°,
∴α=36°,∴∠CED=2×36°=72°,
又∵∠CED=∠A=72°,∴AB∥DE(内错角相等,两直线平行).
25、(2021春 工业园区期末)如图,在四边形中,与互补,、分别平分、,与相交于点.
(1)与有怎样的数量关系?说明理由;
(2)若,,求的度数.
【分析】(1)根据四边形的内角和为以及补角的定义可得,再根据角平分线的定义以及平行线的性质即可得出;
(2)根据与互补可得的度数,根据与互余可得的度数,根据平行线的性质可得的度数,然后根据三角形的内角和以及角的和差关系计算即可.
【解析】(1)与互余.
四边形的内角和为,与互补,
,
、分别平分、,
,,
,,
,即与互余.
(2)由(1)知,,
,,与互补,,,
,,
平分,,
,.
26、如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAP=∠CAB,∠CDP=∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
(1)证明:在图1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,∴∠A+∠C=∠B+∠D;
(2)解:①3;4;故答案为:3,4;
②以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,
以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP
∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,
∵AP、DP分别平分∠CAB和∠BDC,
∴∠BAP=∠CAP,∠CDP=∠BDP,∴2∠P=∠B+∠C,
∵∠B=100°,∠C=120°,∴∠P=(∠B+∠C)=(100°+120°)=110°;
③3∠P=∠B+2∠C,其理由是:
∵∠CAP=∠CAB,∠CDP=∠CDB,∴∠BAP=∠CAB,∠BDP=∠CDB,
以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,
以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP
∴∠C﹣∠P=∠CDP﹣∠CAP=(∠CDB﹣∠CAB),
∠P﹣∠B=∠BDP﹣∠BAP=(∠CDB﹣∠CAB).
∴2(∠C﹣∠P)=∠P﹣∠B,∴3∠P=∠B+2∠C.
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、(2020春 广陵区校级期中)下列车标,可看作图案的某一部分经过平移所形成的是( )
A.B.C.D.
2、下列运算正确的是( )
A.4a3﹣a3=3a3 B.a4 a4=a16 C.(3a)2=6a2 D.a6÷a2=a3
3、(2020春 江阴市期中)已知三角形的三边长分别为2、x、3,则x可能是( )
A.5 B.1 C.6 D.4
4、(2020春 南京期中)计算:( 3)2=2 (3)2=2 6=8,其中,第一步运算的依据是( )
A.同底数幂的乘法法则 B.幂的乘方法则
C.乘法分配律 D.积的乘方法则
5、(﹣0.125)2018×82019等于( )
A.﹣8 B.8 C.0.125 D.﹣0.125
6、若(ambn)3=a9b15,则m、n的值分别为( )
A.9;5 B.3;5 C.5;3 D.6;12
7、(2020春 仪征市期中)如图,∠1=80°,要使得m∥n,则∠2的度数是( )
A.120° B.110° C.100° D.80°
8、(2020春 江阴市期中)如图,在下列给出的条件中,不能判定AB∥DF的是( )
A.∠A=∠3 B.∠A+∠2=180° C.∠1=∠4 D.∠1=∠A
9、(2020秋 苏州期中)将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形(△ABC),BC为折痕,若∠1=42°,则∠2的度数为( )
A.48° B.58° C.60° D.69°
10、(2020春 江阴市期中)如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=68°,则∠AED的度数是( )
A.88° B.98° C.92° D.112°
二、填空题
11、计算:﹣b3 b2= .
12、一种细菌的半径是0.000045米,该数字用科学记数法表示为 .
13、比较大小:()﹣2 ()﹣2.(填“>”“=”或“<”)
14、(2020春 沙坪坝区校级月考)计算82×42021×(﹣0.25)2019的值等于 .
15、若ma=2,mb=3,mc=4,则m2a+b﹣c= .
16、(2021春 镇江期中)如图,已知为的中线,,,的周长为,则的周长为 .
17、(2020秋 溧阳市期中)如图,△DEF是由△ABC沿直线BC向右平移得到,若BC=6,当点E刚好移动到BC的中点时,则CF= .
18、(2020·睢宁县期中)如图,已知AB∥CD,则∠,∠,∠之间的等量关系为( )
A.∠+∠-∠=180° B.∠+∠-∠=180°
C.∠+∠+∠=360° D.∠+∠+∠=180°
三、解答题
19、计算
(1)(a2)3﹣a3 a3+(2a3)2; (2)(﹣4am+1)3÷[2(2am)2 a].
(3)(m﹣n)2 (n﹣m)3 (n﹣m)4 (4)(b2n)3(b3)4n÷(b5)n+1
(5)(﹣1)2019+(π﹣3.14)0﹣()﹣1. (6)(﹣2x2y)3﹣(﹣2x3y)2+6x6y3+2x6y2
20、如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
(1)画出△A′B′C′;
(2)画出AB边上的中线CD和高线CE;(利用网格点和直尺画图)
(3)△BCD的面积为 .
21、已知x2n=4,求(x3n)2﹣xn的值.(其中x为正数,n为正整数)
22、请探索使得等式(2x+3)x+2020=1成立的x的值.
23、(1)已知am=2,an=3,求①am+n的值;②a3m﹣2n的值
(2)已知2×8x×16=223,求x的值.
24、如图,BD∥EF,AE与BD交于点C,∠B=36°,∠A=72°,∠DEF=∠CEF,判断AB与DE是否平行,并说明理由.
25、(2021春 工业园区期末)如图,在四边形中,与互补,、分别平分、,与相交于点.
(1)与有怎样的数量关系?说明理由;
(2)若,,求的度数.
26、如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAP=∠CAB,∠CDP=∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
7~8章 阶段练(2)(基础)【平面图形的认识(二)、幂的运算】
-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、(2020春 广陵区校级期中)下列车标,可看作图案的某一部分经过平移所形成的是( )
A.B.C.D.
解:选项A,B,C不能由基本图形平移得到,选项B是由基本图形圆平移得到,
故选:D.
2、下列运算正确的是( )
A.4a3﹣a3=3a3 B.a4 a4=a16 C.(3a)2=6a2 D.a6÷a2=a3
解:A、4a3﹣a3=3a3,故选项正确;
B、a4×a4=a8,故选项错误;
C(3a)2=9a2,故选项错误;
D、a6÷a2=a4,故选项错误;
故选:A.
3、(2020春 江阴市期中)已知三角形的三边长分别为2、x、3,则x可能是( )
A.5 B.1 C.6 D.4
解:∵2+3=5,3﹣2=1,
∴1<x<5.
故选:D.
4、(2020春 南京期中)计算:( 3)2=2 (3)2=2 6=8,其中,第一步运算的依据是( )
A.同底数幂的乘法法则 B.幂的乘方法则
C.乘法分配律 D.积的乘方法则
解:计算:(a a3)2=a2 (a3)2=a2 a6=a8,其中,第一步运算的依据是积的乘方法则.
故选:D.
5、(﹣0.125)2018×82019等于( )
A.﹣8 B.8 C.0.125 D.﹣0.125
解:(﹣0.125)2018×82019=(﹣0.125)2018×82018×8=(﹣0.125×8)2018×8=1×8=8,
故选:B.
6、若(ambn)3=a9b15,则m、n的值分别为( )
A.9;5 B.3;5 C.5;3 D.6;12
解:∵(ambn)3=a9b15,
∴a3mb3n=a9b15,
∴3m=9,3n=15,
∴m=3,n=5,
故选:B.
7、(2020春 仪征市期中)如图,∠1=80°,要使得m∥n,则∠2的度数是( )
A.120° B.110° C.100° D.80°
解:∵∠1=80°,m∥n,
∴∠3=∠1=80°,
∴∠2=180°﹣∠3=100°.
故选:C.
8、(2020春 江阴市期中)如图,在下列给出的条件中,不能判定AB∥DF的是( )
A.∠A=∠3 B.∠A+∠2=180° C.∠1=∠4 D.∠1=∠A
解:A、因为∠A=∠3,所以AB∥DF(同位角相等,两直线平行),故本选项不符合题意.
B、因为∠A+∠2=180,所以AB∥DF(同旁内角互补,两直线平行),故本选项不符合题意.
C、因为∠1=∠4,所以AB∥DF(内错角相等,两直线平行),故本选项不符合题意.
D、因为∠1=∠A,所以AC∥DE(同位角相等,两直线平行),不能证出AB∥DF,故本选项符合题意.
故选:D.
9、(2020秋 苏州期中)将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形(△ABC),BC为折痕,若∠1=42°,则∠2的度数为( )
A.48° B.58° C.60° D.69°
解:如右图所示,
∵长方形的两条长边平行,∠1=42°,
∴∠1=∠4=42°,∠4=∠5,
∴∠5=42°,
由折叠的性质可知,∠2=∠3,
∵∠2+∠3+∠5=180°,
∴∠2=69°,
故选:D.
10、(2020春 江阴市期中)如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=68°,则∠AED的度数是( )
A.88° B.98° C.92° D.112°
解:根据多边形外角和定理得到:∠1+∠2+∠3+∠4+∠5=360°,
∴∠5=360°﹣4×68°=88°,
∴∠AED=180°﹣∠5=180°﹣88°=92°.
故选:C.
二、填空题
11、计算:﹣b3 b2= .
解:原式=﹣b3+2=﹣b5,
故答案为:﹣b5
12、一种细菌的半径是0.000045米,该数字用科学记数法表示为 .
解:0.000045米用科学记数法表示为4.5×10﹣5米.
故答案为:4.5×10﹣5米.
13、比较大小:()﹣2 ()﹣2.(填“>”“=”或“<”)
解:∵()﹣2=4、()﹣2=9,
∴()﹣2<()﹣2,
故答案为:<.
14、(2020春 沙坪坝区校级月考)计算82×42021×(﹣0.25)2019的值等于 .
【分析】根据幂的乘方与积的乘方进行计算即可.
【解答】解:原式=82×42×42019×(﹣0.25)2019
=82×42×(4×﹣0.25)2019
=82×42×(﹣1)
=﹣1024.
故答案为:﹣1024.
15、若ma=2,mb=3,mc=4,则m2a+b﹣c= .
解:∵ma=2,mb=3,mc=4,
∴m2a+b﹣c=(ma)2 mb÷mc=4×3÷4=3.
故答案为:3.
16、(2021春 镇江期中)如图,已知为的中线,,,的周长为,则的周长为 .
【分析】根据三角形中线的定义可得,再表示出和的周长的差就是、的差,然后计算即可.
【解析】是边上的中线,
,
和周长的差,
的周长为,比长,
周长为:.
故答案为23.
17、(2020秋 溧阳市期中)如图,△DEF是由△ABC沿直线BC向右平移得到,若BC=6,当点E刚好移动到BC的中点时,则CF= .
【分析】根据平移性质得出BC=EF,BE=CF,进而解答即可.
【解析】由平移的性质可得:BC=EF,BE=CF,
∵BC=6,点E刚好移动到BC的中点,
∴BE=EC=CF=3,
故答案为:3.
18、(2020·睢宁县期中)如图,已知AB∥CD,则∠,∠,∠之间的等量关系为( )
A.∠+∠-∠=180° B.∠+∠-∠=180°
C.∠+∠+∠=360° D.∠+∠+∠=180°
【答案】C
【提示】过E点作EF∥AB,则EF∥CD,利用平行线性质可得∠α+∠BEF=180°,∠γ+∠DEF=180°,
根据∠BEF+∠DEF=∠β进一步计算即可得出答案.
【详解】如图所示,过E点作EF∥AB,
∵AB∥CD,∴EF∥CD,∴∠γ+∠DEF=180°,
∵EF∥AB,∴∠α+∠BEF=180°,∴∠γ+∠DEF+∠α+∠BEF=360°,
∵∠BEF+∠DEF=∠β,∴∠α+∠β+∠γ=360°, 故选:C.
三、解答题
19、计算
(1)(a2)3﹣a3 a3+(2a3)2; (2)(﹣4am+1)3÷[2(2am)2 a].
(3)(m﹣n)2 (n﹣m)3 (n﹣m)4 (4)(b2n)3(b3)4n÷(b5)n+1
(5)(﹣1)2019+(π﹣3.14)0﹣()﹣1. (6)(﹣2x2y)3﹣(﹣2x3y)2+6x6y3+2x6y2
解:(1)(a2)3﹣a3 a3+(2a3)2 =a6﹣a6+4a6=4a6;
(2)(﹣4am+1)3÷[2(2am)2 a]=﹣64a3m+3÷8a2m+1=﹣8am+2
(3)(m﹣n)2 (n﹣m)3 (n﹣m)4 =(n﹣m)2+3+4=(n﹣m)9;
(4)(b2n)3(b3)4n÷(b5)n+1=b6n b12n÷b5n+5=b6n+12n﹣5n﹣5=b13n﹣5;
(5)原式=﹣1+1﹣3=﹣3;
(6)原式=﹣8x6y3﹣4x6y2+6x6y3+2x6y2=﹣2x6y3﹣2x6y2.
20、如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
(1)画出△A′B′C′;
(2)画出AB边上的中线CD和高线CE;(利用网格点和直尺画图)
(3)△BCD的面积为 .
【分析】(1)将三角形的三顶点分别向右平移4个单位得到对应点,再顺次连接可得;
(2)根据中线和高的定义作图可得;
(3)利用割补法求解可得.
【详解】解:(1)如图所示,△A′B′C′即为所求;
(2)如图所示,CD、CE即为所求;
(3)△BCD的面积为×4×4﹣×1×3﹣×1×3﹣1=4,
故答案为:4
21、已知x2n=4,求(x3n)2﹣xn的值.(其中x为正数,n为正整数)
解:∵x2n=4,x为正数,n为正整数,
∴xn=2,
∴(x3n)2﹣xn=(xn)6﹣xn=26﹣2=62.
22、请探索使得等式(2x+3)x+2020=1成立的x的值.
解:当x+2020=0时,∴x=﹣2020,∴2x+3=﹣4037≠0,符合题意,
当2x+3=1时,∴x=﹣1,符合题意,
当2x+3=﹣1时,∴x=﹣2,∴x+2020=2018,符合题意,
综上所述,x=﹣2或x=﹣1或x=﹣2020.
23、(1)已知am=2,an=3,求①am+n的值;②a3m﹣2n的值
(2)已知2×8x×16=223,求x的值.
解:(1)①am+n=am an=2×3=6;
②a3m﹣2n=a3m÷a2n=(am)3÷(an)2=23÷32=;
(2)∵2×8x×16=223
∴2×(23)x×24=223,
∴2×23x×24=223,
∴1+3x+4=23,
解得:x=6.
24、如图,BD∥EF,AE与BD交于点C,∠B=36°,∠A=72°,∠DEF=∠CEF,判断AB与DE是否平行,并说明理由.
解:AB与DE平行,理由如下:
∵∠B=36°,∠A=72°,∴∠ACB=∠DCE=180°﹣36°﹣72°=72°,
又∵BD∥EF,∴∠DEF=∠CDE,
又∵∠DEF=∠CEF,若设∠DEF=α,则∠CDE=α,∠CED=2α,
∴在△CED中,∠DCE+∠CDE+CED=180°,即,72°+α+2α=180°,
∴α=36°,∴∠CED=2×36°=72°,
又∵∠CED=∠A=72°,∴AB∥DE(内错角相等,两直线平行).
25、(2021春 工业园区期末)如图,在四边形中,与互补,、分别平分、,与相交于点.
(1)与有怎样的数量关系?说明理由;
(2)若,,求的度数.
【分析】(1)根据四边形的内角和为以及补角的定义可得,再根据角平分线的定义以及平行线的性质即可得出;
(2)根据与互补可得的度数,根据与互余可得的度数,根据平行线的性质可得的度数,然后根据三角形的内角和以及角的和差关系计算即可.
【解析】(1)与互余.
四边形的内角和为,与互补,
,
、分别平分、,
,,
,,
,即与互余.
(2)由(1)知,,
,,与互补,,,
,,
平分,,
,.
26、如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAP=∠CAB,∠CDP=∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
(1)证明:在图1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,∴∠A+∠C=∠B+∠D;
(2)解:①3;4;故答案为:3,4;
②以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,
以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP
∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,
∵AP、DP分别平分∠CAB和∠BDC,
∴∠BAP=∠CAP,∠CDP=∠BDP,∴2∠P=∠B+∠C,
∵∠B=100°,∠C=120°,∴∠P=(∠B+∠C)=(100°+120°)=110°;
③3∠P=∠B+2∠C,其理由是:
∵∠CAP=∠CAB,∠CDP=∠CDB,∴∠BAP=∠CAB,∠BDP=∠CDB,
以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,
以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP
∴∠C﹣∠P=∠CDP﹣∠CAP=(∠CDB﹣∠CAB),
∠P﹣∠B=∠BDP﹣∠BAP=(∠CDB﹣∠CAB).
∴2(∠C﹣∠P)=∠P﹣∠B,∴3∠P=∠B+2∠C.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
