苏教版数学五下 7.1解决问题策略(1)课件
文档属性
| 名称 | 苏教版数学五下 7.1解决问题策略(1)课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 24.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 09:44:37 | ||
图片预览


文档简介
(共19张PPT)
解决问题策略
第七单元 第1课时
苏教版五年级下册数学课件
学习目标
感受数学与生活的联系,增强数学学习的信心。
使学生经历有具体到抽象的认识、理解分数意义的过程,体会图形的变化。
使学生认识转化的策略,学会用转化的策略分析问题并确定解决问题的思路,能根据问题的特点采用转化的具体方法解决问题。
情境导入
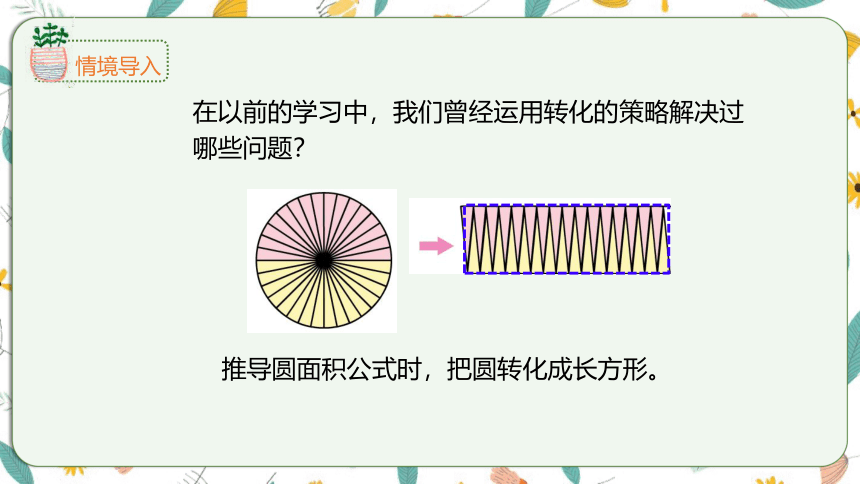
在以前的学习中,我们曾经运用转化的策略解决过哪些问题?
推导圆面积公式时,把圆转化成长方形。
情境导入
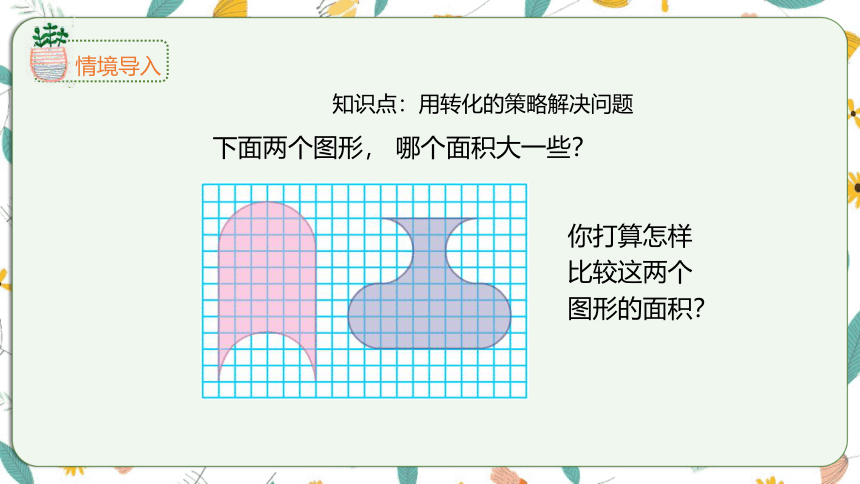
下面两个图形, 哪个面积大一些?
你打算怎样比较这两个图形的面积?
知识点:用转化的策略解决问题
讲授新课
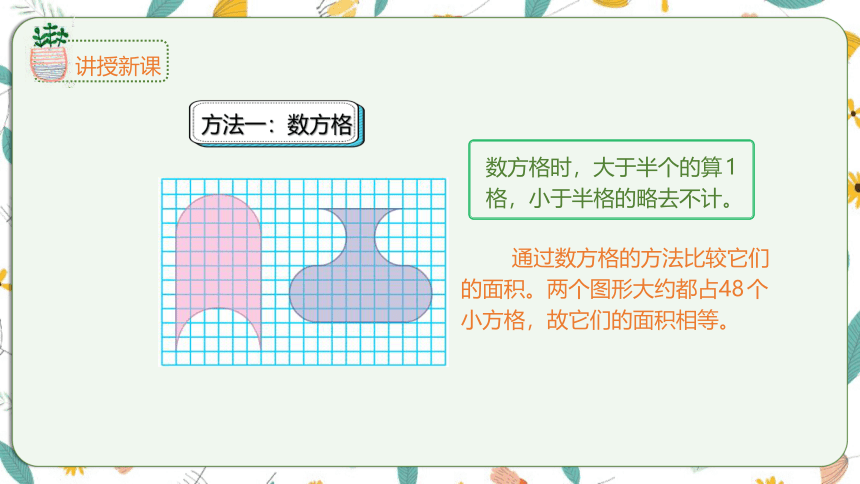
方法一:数方格
数方格时,大于半个的算1格,小于半格的略去不计。
通过数方格的方法比较它们的面积。两个图形大约都占48个小方格,故它们的面积相等。
讲授新课
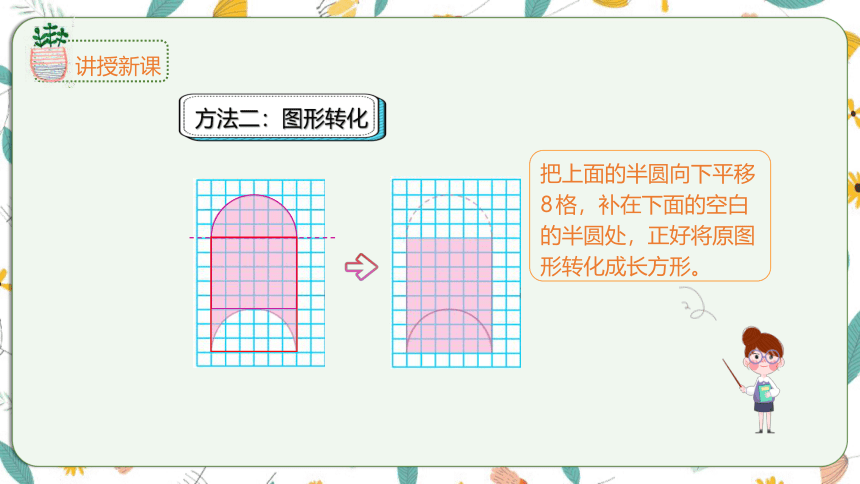
把上面的半圆向下平移8格,补在下面的空白的半圆处,正好将原图形转化成长方形。
方法二:图形转化
讲授新课
因为两个长方形面积相等,所以原来两个图形面积相等。
1.解决例1提出的问题,我们应用了什么策略?
平移,旋转
2.用什么方法把不规则图形转化成规则图形?
转化
3.转化后的图形和转化前比,什么变了?
什么没变?
形状变了,大小没变
讲授新课
讲授新课
解决此类问题可以运用转化的策略将不规则的图形转化成规则的图形后,再进行计算和比较。转化时可以运用平移、旋转等方法。转化后的图形与转化前相比,形状变了,大小没有变。
当堂练习
1.用分数表示各图中的涂色部分。
1
4
1
2
5
8
当堂练习
2.
求下列各图中阴影部分的面积。(单位:cm)
10×5=50(cm )
2×2=4(cm )
3.14×(6÷2) ÷2+3.14×(8÷2)
=39.25(cm )
当堂练习
3.一块草坪被4条1米宽的小路平均分成了9小块。草坪的面积是多少平方米?
答:草坪的面积是1075平方米。
1×2=2(米)
(45-2)×(27-2)
=43×25
=1075(平方米)
当堂练习
图中,4个扇形的半径相等,均为3厘米,求涂色部分的面积。
3.14×3 =28.26(平方厘米)
当堂练习
3.14×r =62.8
解:设圆的半径为r。
r =20
正方形的面积为:
r ÷2×4=20÷2×4=40(cm )
答:正方形的面积是40平方厘米。
5.
如右图所示,已知圆的面积是62.8平方厘米,求正方形的面积。
当堂练习
6.观察下面两个图形,要求右边图形的周长,怎样计算比较简便?如果每个小方格的边长是1厘米,右边图形的周长是多少厘米?
将右边图形中的某些线经过平移可以得到左边图形,所以它的周长与左边图形的周长相等,为(5+3)×2=16(厘米)。
当堂练习
7.
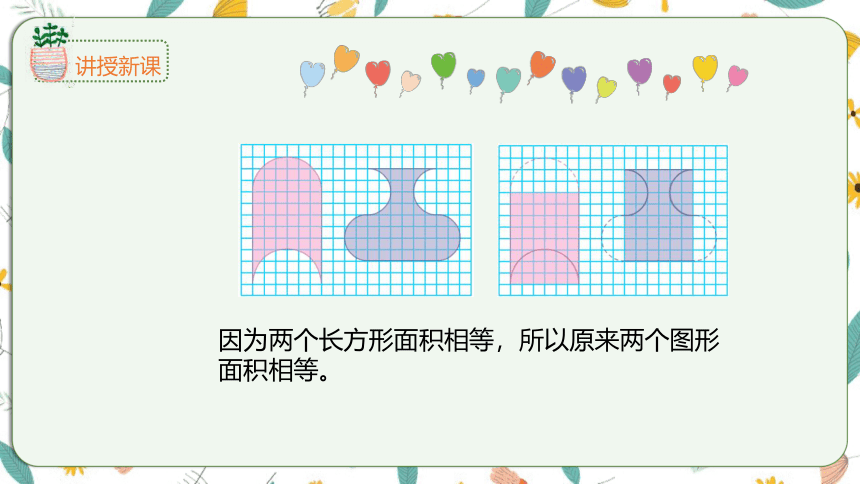
明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?为什么?
这两个图案的面积相等。
当堂小结
我们在计算不规则图形的周长或面积时,可以采用转化的策略,将不规则图形转化成规则的图形,再进行计算。
课后作业
教材109页。
同学们,下课啦~
苏教版年级下册数学课件
解决问题策略
第七单元 第1课时
苏教版五年级下册数学课件
学习目标
感受数学与生活的联系,增强数学学习的信心。
使学生经历有具体到抽象的认识、理解分数意义的过程,体会图形的变化。
使学生认识转化的策略,学会用转化的策略分析问题并确定解决问题的思路,能根据问题的特点采用转化的具体方法解决问题。
情境导入
在以前的学习中,我们曾经运用转化的策略解决过哪些问题?
推导圆面积公式时,把圆转化成长方形。
情境导入
下面两个图形, 哪个面积大一些?
你打算怎样比较这两个图形的面积?
知识点:用转化的策略解决问题
讲授新课
方法一:数方格
数方格时,大于半个的算1格,小于半格的略去不计。
通过数方格的方法比较它们的面积。两个图形大约都占48个小方格,故它们的面积相等。
讲授新课
把上面的半圆向下平移8格,补在下面的空白的半圆处,正好将原图形转化成长方形。
方法二:图形转化
讲授新课
因为两个长方形面积相等,所以原来两个图形面积相等。
1.解决例1提出的问题,我们应用了什么策略?
平移,旋转
2.用什么方法把不规则图形转化成规则图形?
转化
3.转化后的图形和转化前比,什么变了?
什么没变?
形状变了,大小没变
讲授新课
讲授新课
解决此类问题可以运用转化的策略将不规则的图形转化成规则的图形后,再进行计算和比较。转化时可以运用平移、旋转等方法。转化后的图形与转化前相比,形状变了,大小没有变。
当堂练习
1.用分数表示各图中的涂色部分。
1
4
1
2
5
8
当堂练习
2.
求下列各图中阴影部分的面积。(单位:cm)
10×5=50(cm )
2×2=4(cm )
3.14×(6÷2) ÷2+3.14×(8÷2)
=39.25(cm )
当堂练习
3.一块草坪被4条1米宽的小路平均分成了9小块。草坪的面积是多少平方米?
答:草坪的面积是1075平方米。
1×2=2(米)
(45-2)×(27-2)
=43×25
=1075(平方米)
当堂练习
图中,4个扇形的半径相等,均为3厘米,求涂色部分的面积。
3.14×3 =28.26(平方厘米)
当堂练习
3.14×r =62.8
解:设圆的半径为r。
r =20
正方形的面积为:
r ÷2×4=20÷2×4=40(cm )
答:正方形的面积是40平方厘米。
5.
如右图所示,已知圆的面积是62.8平方厘米,求正方形的面积。
当堂练习
6.观察下面两个图形,要求右边图形的周长,怎样计算比较简便?如果每个小方格的边长是1厘米,右边图形的周长是多少厘米?
将右边图形中的某些线经过平移可以得到左边图形,所以它的周长与左边图形的周长相等,为(5+3)×2=16(厘米)。
当堂练习
7.
明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?为什么?
这两个图案的面积相等。
当堂小结
我们在计算不规则图形的周长或面积时,可以采用转化的策略,将不规则图形转化成规则的图形,再进行计算。
课后作业
教材109页。
同学们,下课啦~
苏教版年级下册数学课件
