2021-2022学年北师大版九年级数学下册3.1-3.5检测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.1-3.5检测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 327.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 12:17:42 | ||
图片预览



文档简介
北师大版九年级数学下册第三章圆3.1-3.5 检测试卷
一.选择题
1.若⊙O的半径是4cm,点A在⊙O内,则OA的长可能是( ).
A.4cm B.6cm C.3cm D.10cm
2.下列各组图形中,四个顶点一定在同一圆上的是( ).
A.矩形,菱形 B.矩形,正方形
C.菱形,正方形 D.平行四边形,菱形
3.如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( ).
A.100° B.72° C.64° D.36°
4.已知,如图,∠AOB=∠COD,下列结论不一定成立的是( ).
A.AB=CD B.=
C.△AOB≌△COD D.△AOB、△COD都是等边三角形
5.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( ).
A.51° B.56° C.68° D.78°
6.点P是⊙O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为( ).
A.3cm B.4cm C.5cm D.6cm
7.下列命题中是真命题的有( )
①两个端点能够重合的弧是等弧;②圆的任意一条弦把圆分成优弧和劣弧两部分;③长度相等的弧是等弧;④半径相等的两个圆是等圆;⑤直径是圆中最长的弦.
A.5个 B.4个 C.3个 D.2个
8.如图,AB、CD是⊙O的两条弦,OE⊥AB于E,OF⊥CD于F.如果AB=CD,那么下列判断中错误的是( ).
A. B.∠AOB=∠COD C.OE=OF D.∠AOC=∠BOD
9.如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2,CD=1,则BE的长是( ).
A.5 B.6 C.7 D.8
10.如图,点C是以点O为圆心,AB为直径的半圆上一点,连接AC,BC,OC.若AC=4,BC=3,则sin∠BOC的值是( )
A.1 B. C. D.
11.量角器测角度时摆放的位置如图所示,在△AOB中,射线OC交边AB于点D,则∠ADC的度数为( )
A.60° B.70° C.80° D.85°
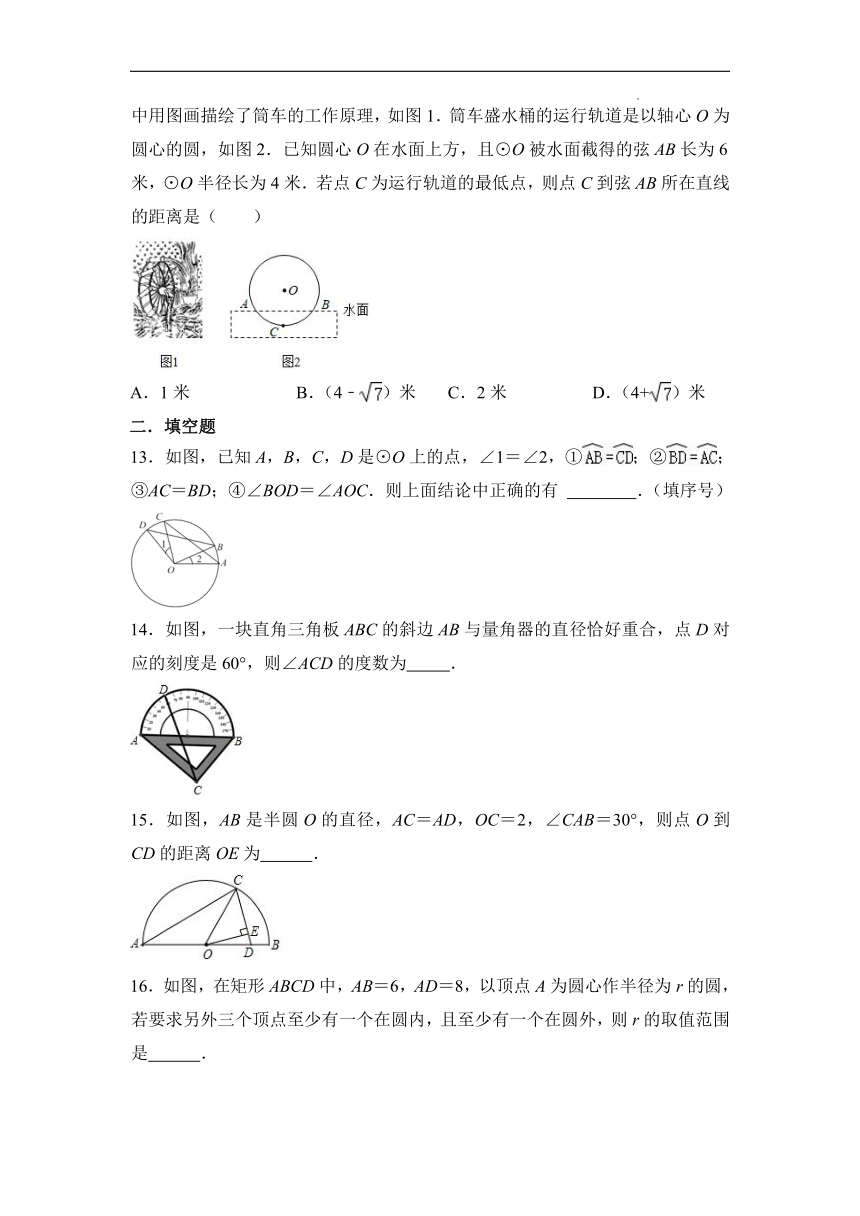
12.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米 B.(4﹣)米 C.2米 D.(4+)米
二.填空题
13.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,①;②;③AC=BD;④∠BOD=∠AOC.则上面结论中正确的有 .(填序号)
14.如图,一块直角三角板ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是60°,则∠ACD的度数为 .
15.如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE为 .
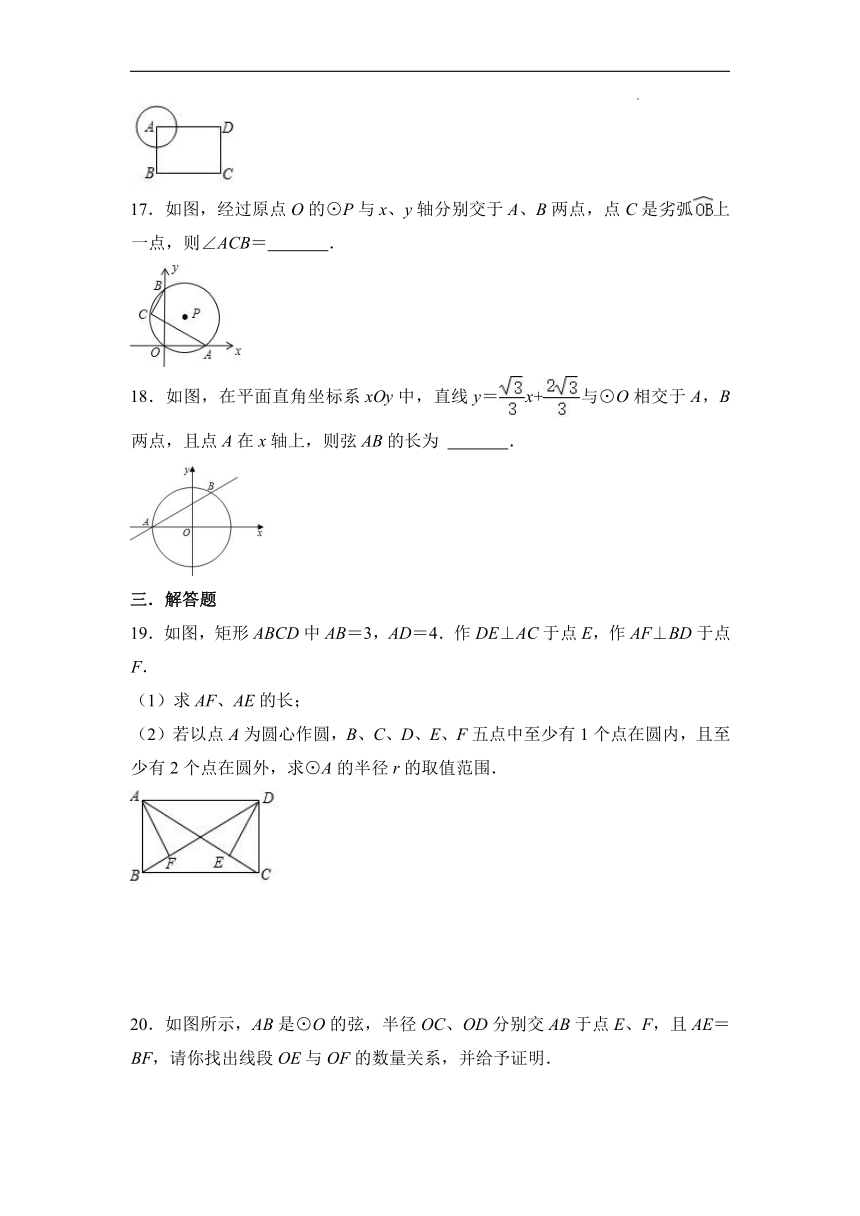
16.如图,在矩形ABCD中,AB=6,AD=8,以顶点A为圆心作半径为r的圆,若要求另外三个顶点至少有一个在圆内,且至少有一个在圆外,则r的取值范围是 .
17.如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧上一点,则∠ACB= .
18.如图,在平面直角坐标系xOy中,直线y=x+与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
三.解答题
19.如图,矩形ABCD中AB=3,AD=4.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF、AE的长;
(2)若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求⊙A的半径r的取值范围.
20.如图所示,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.
21.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.
22.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
23.如图,在△ABC中,∠BAC=90°,点E在BC边上,过A,C,E三点的⊙O交AB边于另一点F,且F是的中点,AD是⊙O的一条直径,连接DE并延长交AB边于M点.
(1)求证:四边形CDMF为平行四边形;
(2)当CD=AB时,求sin∠ACF的值.
24.如图,已知ED为⊙O的直径且ED=4,点A(不与E、D重合)为⊙O上一个动点,线段AB经过点E,且EA=EB,F为⊙O上一点,∠FEB=90°,BF的延长线交AD的延长线交于点C.
(1)求证:△EFB≌△ADE;
(2)当点A在⊙O上移动时,直接回答四边形FCDE的最大面积为多少.
北师大版九年级数学下册第三章圆3.1-3.4 检测试卷答案提示
一.选择题
1.若⊙O的半径是4cm,点A在⊙O内,则OA的长可能是( )选:C.
A.4cm B.6cm C.3cm D.10cm
2.下列各组图形中,四个顶点一定在同一圆上的是( )选:B.
A.矩形,菱形 B.矩形,正方形
C.菱形,正方形 D.平行四边形,菱形
3.如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )选:C.
A.100° B.72° C.64° D.36°
4.已知,如图,∠AOB=∠COD,下列结论不一定成立的是( )选:D.
A.AB=CD B.=
C.△AOB≌△COD D.△AOB、△COD都是等边三角形
5.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( )选:A.
A.51° B.56° C.68° D.78°
6.点P是⊙O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为( )选:B.
A.3cm B.4cm C.5cm D.6cm
7.下列命题中是真命题的有( )
①两个端点能够重合的弧是等弧;②圆的任意一条弦把圆分成优弧和劣弧两部分;③长度相等的弧是等弧;④半径相等的两个圆是等圆;⑤直径是圆中最长的弦.
A.5个 B.4个 C.3个 D.2个
解:能够重合的弧是等弧,①是假命题;
圆的任意一条不是直径的弦把圆分成优弧和劣弧两部分,②是假命题;
长度相等的弧不一定是等弧,③是假命题;
半径相等的两个圆是等圆,④是真命题;
直径是圆中最长的弦,⑤是真命题;
故选:D.
8.如图,AB、CD是⊙O的两条弦,OE⊥AB于E,OF⊥CD于F.如果AB=CD,那么下列判断中错误的是( )选:D.
A. B.∠AOB=∠COD C.OE=OF D.∠AOC=∠BOD
9.如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2,CD=1,则BE的长是( )选:B.
A.5 B.6 C.7 D.8
10.如图,点C是以点O为圆心,AB为直径的半圆上一点,连接AC,BC,OC.若AC=4,BC=3,则sin∠BOC的值是( )
A.1 B. C. D.
解:如图,过点C作CH⊥AB于H.
∵AB是直径,
∴∠ACB=90°,
∵AC=4,BC=3,
∴AB===5,
∴OC=AB=,
∵S△ABC= AB CH= AC BC,
∴CH==,
∴sin∠BOC===,
故选:B.
11.量角器测角度时摆放的位置如图所示,在△AOB中,射线OC交边AB于点D,则∠ADC的度数为( )
A.60° B.70° C.80° D.85°
解:∵OA=OB,∠AOB=140°,
∴∠A=∠B=(180°﹣140°)=20°,
∵∠AOC=60°,
∴∠ADC=∠A+∠AOC=20°+60°=80°,
故选:C.
12.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米 B.(4﹣)米 C.2米 D.(4+)米
解:连接OC交AB于D,连接OA,
∵点C为运行轨道的最低点,
∴OC⊥AB,
∴AD=AB=3(米),
在Rt△OAD中,OD===(米),
∴点C到弦AB所在直线的距离CD=OC﹣OD=(4﹣)米,
故选:B.
二.填空题
13.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,①;②;③AC=BD;④∠BOD=∠AOC.则上面结论中正确的有 ①②③④ .(填序号)
14.如图,一块直角三角板ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是60°,则∠ACD的度数为 30° .
15.如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE为 .
16.如图,在矩形ABCD中,AB=6,AD=8,以顶点A为圆心作半径为r的圆,若要求另外三个顶点至少有一个在圆内,且至少有一个在圆外,则r的取值范围是 6<r<10 .
17.如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧上一点,则∠ACB= 90° .
18.如图,在平面直角坐标系xOy中,直线y=x+与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 2 .
解:设直线AB交y轴于C,过O作OD⊥AB于D,如图:
在y=x+中,令x=0得y=,
∴C(0,),OC=,
在y=x+中令y=0得x+=0,
解得x=﹣2,
∴A(﹣2,0),OA=2,
Rt△AOC中,tan∠CAO===,
∴∠CAO=30°,
Rt△AOD中,AD=OA cos30°=2×=,
∵OD⊥AB,
∴AD=BD=,
∴AB=2,
故答案为:2.
三.解答题
19.如图,矩形ABCD中AB=3,AD=4.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF、AE的长;
(2)若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求⊙A的半径r的取值范围.
解:(1)∵矩形ABCD中AB=3,AD=4,
∴AC=BD==5,
∵AF BD=AB AD,
∴AF==,
同理可得DE=,
在Rt△ADE中,AE==;
(2)∵AF<AB<AE<AD<AC,
∴若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,即点F在圆内,点D、C在圆外,
∴⊙A的半径r的取值范围为2.4<r<4.
20.如图所示,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.
解:OE=OF,
证明:连接OA,OB,
∵OA=OB,
∴∠OAB=∠OBA.即∠OAE=∠OBF.
∴在△OAE与△OBF中,
,
∴△OAE≌△OBF(SAS).
∴OE=OF.
21.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.
(1)证明:过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE﹣DE=AE﹣CE,即AC=BD;
(2)解:由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,
∴OE=6,
∴CE===2,AE===8,
∴AC=AE﹣CE=8﹣2.
22.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
证明:(1)∵C是的中点,
∴,
∵AB是⊙O的直径,且CF⊥AB,
∴,
∴,
∴CD=BF,
在△BFG和△CDG中,
∵,
∴△BFG≌△CDG(AAS);
(2)解法一:如图,连接OF,设⊙O的半径为r,
Rt△ADB中,BD2=AB2﹣AD2,即BD2=(2r)2﹣22,
Rt△OEF中,OF2=OE2+EF2,即EF2=r2﹣(r﹣2)2,
∵,
∴,
∴BD=CF,
∴BD2=CF2=(2EF)2=4EF2,
即(2r)2﹣22=4[r2﹣(r﹣2)2],
解得:r=1(舍)或3,
∴BF2=EF2+BE2=32﹣(3﹣2)2+22=12,
∴BF=2;
解法二:如图,过C作CH⊥AD于H,连接AC、BC,
∵,
∴∠HAC=∠BAC,
∵CE⊥AB,
∴CH=CE,
∵AC=AC,
∴Rt△AHC≌Rt△AEC(HL),
∴AE=AH,
∵CH=CE,CD=CB,
∴Rt△CDH≌Rt△CBE(HL),
∴DH=BE=2,
∴AE=AH=2+2=4,
∴AB=4+2=6,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠BEC=90°,
∵∠EBC=∠ABC,
∴△BEC∽△BCA,
∴,
∴BC2=AB BE=6×2=12,
∴BF=BC=2.
解法三:如图,连接OC,交BD于H,
∵C是的中点,
∴OC⊥BD,
∴DH=BH,
∵OA=OB,
∴OH=AD=1,
∵OC=OB,∠COE=∠BOH,∠OHB=∠OEC=90°,
∴△COE≌△BOH(AAS),
∴OH=OE=1,
∴CE=EF==2,
∴BF===2.
23.如图,在△ABC中,∠BAC=90°,点E在BC边上,过A,C,E三点的⊙O交AB边于另一点F,且F是的中点,AD是⊙O的一条直径,连接DE并延长交AB边于M点.
(1)求证:四边形CDMF为平行四边形;
(2)当CD=AB时,求sin∠ACF的值.
(1)证明:连接DF、EF,
∵∠BAC=90°,
∴FC是⊙O的直径,
∵F是的中点,
∴=,
∴∠ADF=∠EDF,
∵OF=OD,
∴∠ADF=∠OFD,
∴∠OFD=∠EDF,
∴FC∥DM,
∵OA=OD,OF=OC,∠BAC=90°,
∴四边形AFDC为矩形,
∴AF∥CD,
∴四边形CDMF为平行四边形;
(2)解:∵四边形AFDC为矩形,四边形CDMF为平行四边形,
∴CD=AF=FM=EF,
∵CD=AB,
∴CD=(2CD+BM),
∴CD=2BM,
∵BM∥CD,
∴△BEM∽△CED,
∴==,
∴EC=2BE,
设BM=a,则CD=2a,BF=3a,EF=2a,
在Rt△BEF中,BE==a,
∴EC=2a,
在Rt△CEF中,FC==2a,
在Rt△FAC中,sin∠ACF===.
24.如图,已知ED为⊙O的直径且ED=4,点A(不与E、D重合)为⊙O上一个动点,线段AB经过点E,且EA=EB,F为⊙O上一点,∠FEB=90°,BF的延长线交AD的延长线交于点C.
(1)求证:△EFB≌△ADE;
(2)当点A在⊙O上移动时,直接回答四边形FCDE的最大面积为多少.
解:(1)连接FA,
∵∠FEB=90°,
∴EF⊥AB,
∵BE=AE,
∴BF=AF,
∵∠FEA=∠FEB=90°,
∴AF是⊙O的直径,
∴AF=DE,
∴BF=ED,
在Rt△EFB与Rt△ADE中,
,
∴Rt△EFB≌Rt△ADE(HL);
(2)∵Rt△EFB≌Rt△ADE,
∴∠B=∠AED,
∴DE∥BC,
∵ED为⊙O的直径,
∴AC⊥AB,
∵EF⊥AB,
∴EF∥CD,
∴四边形FCDE是平行四边形,
∴E到BC的距离最大时,四边形FCDE的面积最大,
即点A到DE的距离最大,
∴当A为的中点时,
点A到DE的距离最大是2,
∴四边形FCDE的最大面积=4×2=8.
一.选择题
1.若⊙O的半径是4cm,点A在⊙O内,则OA的长可能是( ).
A.4cm B.6cm C.3cm D.10cm
2.下列各组图形中,四个顶点一定在同一圆上的是( ).
A.矩形,菱形 B.矩形,正方形
C.菱形,正方形 D.平行四边形,菱形
3.如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( ).
A.100° B.72° C.64° D.36°
4.已知,如图,∠AOB=∠COD,下列结论不一定成立的是( ).
A.AB=CD B.=
C.△AOB≌△COD D.△AOB、△COD都是等边三角形
5.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( ).
A.51° B.56° C.68° D.78°
6.点P是⊙O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为( ).
A.3cm B.4cm C.5cm D.6cm
7.下列命题中是真命题的有( )
①两个端点能够重合的弧是等弧;②圆的任意一条弦把圆分成优弧和劣弧两部分;③长度相等的弧是等弧;④半径相等的两个圆是等圆;⑤直径是圆中最长的弦.
A.5个 B.4个 C.3个 D.2个
8.如图,AB、CD是⊙O的两条弦,OE⊥AB于E,OF⊥CD于F.如果AB=CD,那么下列判断中错误的是( ).
A. B.∠AOB=∠COD C.OE=OF D.∠AOC=∠BOD
9.如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2,CD=1,则BE的长是( ).
A.5 B.6 C.7 D.8
10.如图,点C是以点O为圆心,AB为直径的半圆上一点,连接AC,BC,OC.若AC=4,BC=3,则sin∠BOC的值是( )
A.1 B. C. D.
11.量角器测角度时摆放的位置如图所示,在△AOB中,射线OC交边AB于点D,则∠ADC的度数为( )
A.60° B.70° C.80° D.85°
12.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米 B.(4﹣)米 C.2米 D.(4+)米
二.填空题
13.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,①;②;③AC=BD;④∠BOD=∠AOC.则上面结论中正确的有 .(填序号)
14.如图,一块直角三角板ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是60°,则∠ACD的度数为 .
15.如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE为 .
16.如图,在矩形ABCD中,AB=6,AD=8,以顶点A为圆心作半径为r的圆,若要求另外三个顶点至少有一个在圆内,且至少有一个在圆外,则r的取值范围是 .
17.如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧上一点,则∠ACB= .
18.如图,在平面直角坐标系xOy中,直线y=x+与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
三.解答题
19.如图,矩形ABCD中AB=3,AD=4.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF、AE的长;
(2)若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求⊙A的半径r的取值范围.
20.如图所示,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.
21.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.
22.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
23.如图,在△ABC中,∠BAC=90°,点E在BC边上,过A,C,E三点的⊙O交AB边于另一点F,且F是的中点,AD是⊙O的一条直径,连接DE并延长交AB边于M点.
(1)求证:四边形CDMF为平行四边形;
(2)当CD=AB时,求sin∠ACF的值.
24.如图,已知ED为⊙O的直径且ED=4,点A(不与E、D重合)为⊙O上一个动点,线段AB经过点E,且EA=EB,F为⊙O上一点,∠FEB=90°,BF的延长线交AD的延长线交于点C.
(1)求证:△EFB≌△ADE;
(2)当点A在⊙O上移动时,直接回答四边形FCDE的最大面积为多少.
北师大版九年级数学下册第三章圆3.1-3.4 检测试卷答案提示
一.选择题
1.若⊙O的半径是4cm,点A在⊙O内,则OA的长可能是( )选:C.
A.4cm B.6cm C.3cm D.10cm
2.下列各组图形中,四个顶点一定在同一圆上的是( )选:B.
A.矩形,菱形 B.矩形,正方形
C.菱形,正方形 D.平行四边形,菱形
3.如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )选:C.
A.100° B.72° C.64° D.36°
4.已知,如图,∠AOB=∠COD,下列结论不一定成立的是( )选:D.
A.AB=CD B.=
C.△AOB≌△COD D.△AOB、△COD都是等边三角形
5.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( )选:A.
A.51° B.56° C.68° D.78°
6.点P是⊙O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为( )选:B.
A.3cm B.4cm C.5cm D.6cm
7.下列命题中是真命题的有( )
①两个端点能够重合的弧是等弧;②圆的任意一条弦把圆分成优弧和劣弧两部分;③长度相等的弧是等弧;④半径相等的两个圆是等圆;⑤直径是圆中最长的弦.
A.5个 B.4个 C.3个 D.2个
解:能够重合的弧是等弧,①是假命题;
圆的任意一条不是直径的弦把圆分成优弧和劣弧两部分,②是假命题;
长度相等的弧不一定是等弧,③是假命题;
半径相等的两个圆是等圆,④是真命题;
直径是圆中最长的弦,⑤是真命题;
故选:D.
8.如图,AB、CD是⊙O的两条弦,OE⊥AB于E,OF⊥CD于F.如果AB=CD,那么下列判断中错误的是( )选:D.
A. B.∠AOB=∠COD C.OE=OF D.∠AOC=∠BOD
9.如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2,CD=1,则BE的长是( )选:B.
A.5 B.6 C.7 D.8
10.如图,点C是以点O为圆心,AB为直径的半圆上一点,连接AC,BC,OC.若AC=4,BC=3,则sin∠BOC的值是( )
A.1 B. C. D.
解:如图,过点C作CH⊥AB于H.
∵AB是直径,
∴∠ACB=90°,
∵AC=4,BC=3,
∴AB===5,
∴OC=AB=,
∵S△ABC= AB CH= AC BC,
∴CH==,
∴sin∠BOC===,
故选:B.
11.量角器测角度时摆放的位置如图所示,在△AOB中,射线OC交边AB于点D,则∠ADC的度数为( )
A.60° B.70° C.80° D.85°
解:∵OA=OB,∠AOB=140°,
∴∠A=∠B=(180°﹣140°)=20°,
∵∠AOC=60°,
∴∠ADC=∠A+∠AOC=20°+60°=80°,
故选:C.
12.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米 B.(4﹣)米 C.2米 D.(4+)米
解:连接OC交AB于D,连接OA,
∵点C为运行轨道的最低点,
∴OC⊥AB,
∴AD=AB=3(米),
在Rt△OAD中,OD===(米),
∴点C到弦AB所在直线的距离CD=OC﹣OD=(4﹣)米,
故选:B.
二.填空题
13.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,①;②;③AC=BD;④∠BOD=∠AOC.则上面结论中正确的有 ①②③④ .(填序号)
14.如图,一块直角三角板ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是60°,则∠ACD的度数为 30° .
15.如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE为 .
16.如图,在矩形ABCD中,AB=6,AD=8,以顶点A为圆心作半径为r的圆,若要求另外三个顶点至少有一个在圆内,且至少有一个在圆外,则r的取值范围是 6<r<10 .
17.如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧上一点,则∠ACB= 90° .
18.如图,在平面直角坐标系xOy中,直线y=x+与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 2 .
解:设直线AB交y轴于C,过O作OD⊥AB于D,如图:
在y=x+中,令x=0得y=,
∴C(0,),OC=,
在y=x+中令y=0得x+=0,
解得x=﹣2,
∴A(﹣2,0),OA=2,
Rt△AOC中,tan∠CAO===,
∴∠CAO=30°,
Rt△AOD中,AD=OA cos30°=2×=,
∵OD⊥AB,
∴AD=BD=,
∴AB=2,
故答案为:2.
三.解答题
19.如图,矩形ABCD中AB=3,AD=4.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF、AE的长;
(2)若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求⊙A的半径r的取值范围.
解:(1)∵矩形ABCD中AB=3,AD=4,
∴AC=BD==5,
∵AF BD=AB AD,
∴AF==,
同理可得DE=,
在Rt△ADE中,AE==;
(2)∵AF<AB<AE<AD<AC,
∴若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,即点F在圆内,点D、C在圆外,
∴⊙A的半径r的取值范围为2.4<r<4.
20.如图所示,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.
解:OE=OF,
证明:连接OA,OB,
∵OA=OB,
∴∠OAB=∠OBA.即∠OAE=∠OBF.
∴在△OAE与△OBF中,
,
∴△OAE≌△OBF(SAS).
∴OE=OF.
21.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.
(1)证明:过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE﹣DE=AE﹣CE,即AC=BD;
(2)解:由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,
∴OE=6,
∴CE===2,AE===8,
∴AC=AE﹣CE=8﹣2.
22.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
证明:(1)∵C是的中点,
∴,
∵AB是⊙O的直径,且CF⊥AB,
∴,
∴,
∴CD=BF,
在△BFG和△CDG中,
∵,
∴△BFG≌△CDG(AAS);
(2)解法一:如图,连接OF,设⊙O的半径为r,
Rt△ADB中,BD2=AB2﹣AD2,即BD2=(2r)2﹣22,
Rt△OEF中,OF2=OE2+EF2,即EF2=r2﹣(r﹣2)2,
∵,
∴,
∴BD=CF,
∴BD2=CF2=(2EF)2=4EF2,
即(2r)2﹣22=4[r2﹣(r﹣2)2],
解得:r=1(舍)或3,
∴BF2=EF2+BE2=32﹣(3﹣2)2+22=12,
∴BF=2;
解法二:如图,过C作CH⊥AD于H,连接AC、BC,
∵,
∴∠HAC=∠BAC,
∵CE⊥AB,
∴CH=CE,
∵AC=AC,
∴Rt△AHC≌Rt△AEC(HL),
∴AE=AH,
∵CH=CE,CD=CB,
∴Rt△CDH≌Rt△CBE(HL),
∴DH=BE=2,
∴AE=AH=2+2=4,
∴AB=4+2=6,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠BEC=90°,
∵∠EBC=∠ABC,
∴△BEC∽△BCA,
∴,
∴BC2=AB BE=6×2=12,
∴BF=BC=2.
解法三:如图,连接OC,交BD于H,
∵C是的中点,
∴OC⊥BD,
∴DH=BH,
∵OA=OB,
∴OH=AD=1,
∵OC=OB,∠COE=∠BOH,∠OHB=∠OEC=90°,
∴△COE≌△BOH(AAS),
∴OH=OE=1,
∴CE=EF==2,
∴BF===2.
23.如图,在△ABC中,∠BAC=90°,点E在BC边上,过A,C,E三点的⊙O交AB边于另一点F,且F是的中点,AD是⊙O的一条直径,连接DE并延长交AB边于M点.
(1)求证:四边形CDMF为平行四边形;
(2)当CD=AB时,求sin∠ACF的值.
(1)证明:连接DF、EF,
∵∠BAC=90°,
∴FC是⊙O的直径,
∵F是的中点,
∴=,
∴∠ADF=∠EDF,
∵OF=OD,
∴∠ADF=∠OFD,
∴∠OFD=∠EDF,
∴FC∥DM,
∵OA=OD,OF=OC,∠BAC=90°,
∴四边形AFDC为矩形,
∴AF∥CD,
∴四边形CDMF为平行四边形;
(2)解:∵四边形AFDC为矩形,四边形CDMF为平行四边形,
∴CD=AF=FM=EF,
∵CD=AB,
∴CD=(2CD+BM),
∴CD=2BM,
∵BM∥CD,
∴△BEM∽△CED,
∴==,
∴EC=2BE,
设BM=a,则CD=2a,BF=3a,EF=2a,
在Rt△BEF中,BE==a,
∴EC=2a,
在Rt△CEF中,FC==2a,
在Rt△FAC中,sin∠ACF===.
24.如图,已知ED为⊙O的直径且ED=4,点A(不与E、D重合)为⊙O上一个动点,线段AB经过点E,且EA=EB,F为⊙O上一点,∠FEB=90°,BF的延长线交AD的延长线交于点C.
(1)求证:△EFB≌△ADE;
(2)当点A在⊙O上移动时,直接回答四边形FCDE的最大面积为多少.
解:(1)连接FA,
∵∠FEB=90°,
∴EF⊥AB,
∵BE=AE,
∴BF=AF,
∵∠FEA=∠FEB=90°,
∴AF是⊙O的直径,
∴AF=DE,
∴BF=ED,
在Rt△EFB与Rt△ADE中,
,
∴Rt△EFB≌Rt△ADE(HL);
(2)∵Rt△EFB≌Rt△ADE,
∴∠B=∠AED,
∴DE∥BC,
∵ED为⊙O的直径,
∴AC⊥AB,
∵EF⊥AB,
∴EF∥CD,
∴四边形FCDE是平行四边形,
∴E到BC的距离最大时,四边形FCDE的面积最大,
即点A到DE的距离最大,
∴当A为的中点时,
点A到DE的距离最大是2,
∴四边形FCDE的最大面积=4×2=8.
