2021-2022学年苏科版七年级数学下册9.3多项式乘多项式提升训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册9.3多项式乘多项式提升训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 171.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 12:18:58 | ||
图片预览


文档简介
9.3多项式乘多项式
一、选择题
1、计算(2m+3)(m﹣1)的结果是( )
A.2m2﹣m﹣3 B.2m2+m﹣3 C.2m2﹣m+3 D.m2﹣m﹣3
2.(2020·浙江杭州市·七年级期中)若a,b,k均为整数,则满足等式的所有k值的个数为( )
A.2个 B.4个 C.6个 D.8个
3如果展开后结果中不含的一次项,则等于
A. B. C. D.
4已知,是常数,若化简的结果不含的二次项,则的值为
A. B. C. D.
5、当x=1时,ax+b+1的值为﹣3,则(a+b﹣1)(3﹣2a﹣2b)的值为( )
A.55 B.﹣55 C.25 D.﹣25
6、若M=(x﹣3)(x﹣4),N=(x﹣1)(x﹣6),则M与N的大小关系为( )
A.M>N B.M=N C.M<N D.由 x 的取值而定
7、如图,在一块长为a米,宽为b米的长方形草地上,有一条弯曲的小路,小路的左边线向右平移2米就是它的右边线,这块草地的绿地面积是(单位:平方米)( )
A.ab B.(a﹣2)b C.a(b﹣2) D.(a﹣2)(b﹣2)
8、如图,现有正方形卡片A类,B类和长方形卡片C类若干张,如果要拼一个长为(a+3b),宽为(a+2b)的大长方形,则需要C类卡片( )
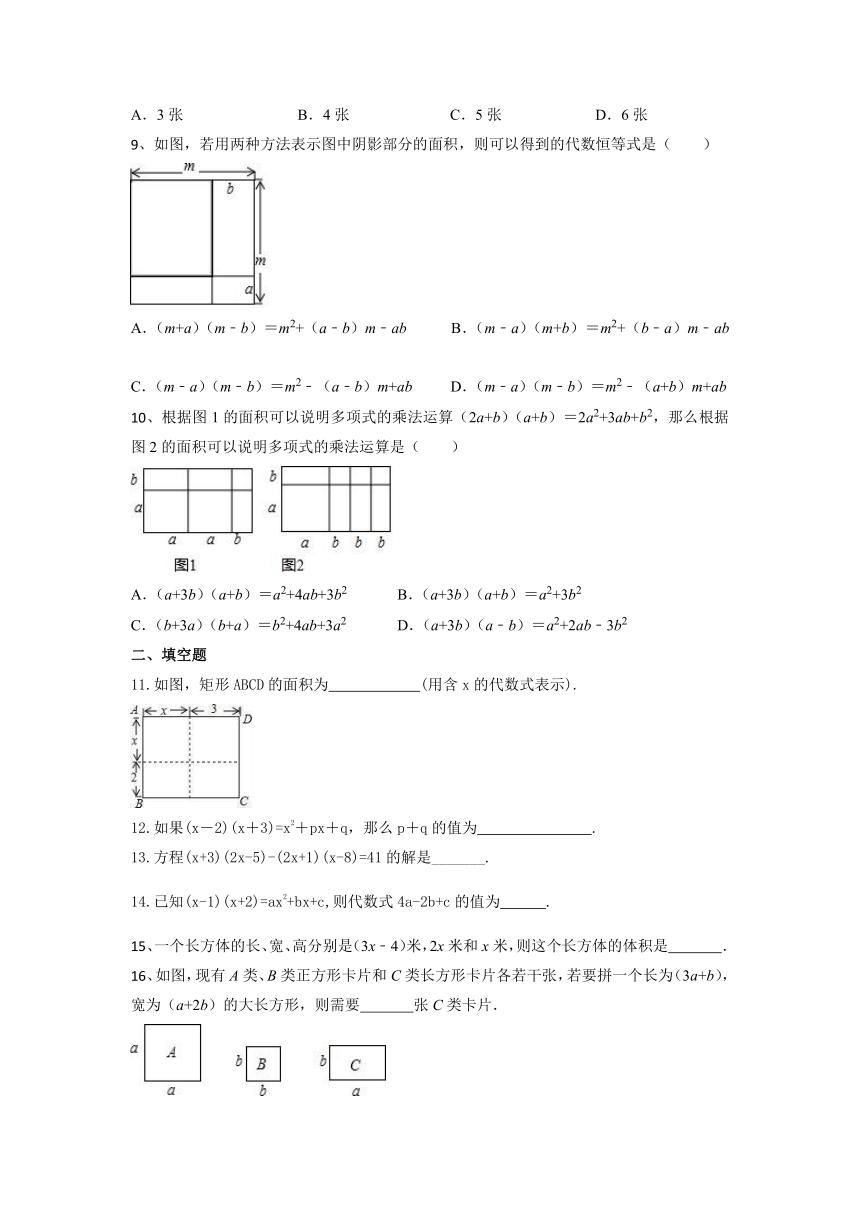
A.3张 B.4张 C.5张 D.6张
9、如图,若用两种方法表示图中阴影部分的面积,则可以得到的代数恒等式是( )
A.(m+a)(m﹣b)=m2+(a﹣b)m﹣ab B.(m﹣a)(m+b)=m2+(b﹣a)m﹣ab
C.(m﹣a)(m﹣b)=m2﹣(a﹣b)m+ab D.(m﹣a)(m﹣b)=m2﹣(a+b)m+ab
10、根据图1的面积可以说明多项式的乘法运算(2a+b)(a+b)=2a2+3ab+b2,那么根据图2的面积可以说明多项式的乘法运算是( )
A.(a+3b)(a+b)=a2+4ab+3b2 B.(a+3b)(a+b)=a2+3b2
C.(b+3a)(b+a)=b2+4ab+3a2 D.(a+3b)(a﹣b)=a2+2ab﹣3b2
二、填空题
11.如图,矩形ABCD的面积为 (用含x的代数式表示).
12.如果(x-2)(x+3)=x2+px+q,那么p+q的值为 .
13.方程(x+3)(2x-5)-(2x+1)(x-8)=41的解是_______.
14.已知(x-1)(x+2)=ax2+bx+c,则代数式4a-2b+c的值为 .
15、一个长方体的长、宽、高分别是(3x﹣4)米,2x米和x米,则这个长方体的体积是 .
16、如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要 张C类卡片.
三、解答题
17、计算:
(1)(2a﹣7)(a+6)﹣(a﹣2)(2a+1)
(2)
(3)
18、先化简,再求值.,其中a,b满足.
19.计算.
(1)(x+y)(2a+b);
(2)(a+b)(a﹣b);
(3) ;
(4)(3x﹣2y)(2x﹣3y);
(5)(3x+2)(﹣x﹣2).
20.若(x2+3mx﹣)(x2﹣3x+n)的积中不含x和x3项,
(1)求m2﹣mn+n2的值;
(2)求代数式(﹣18m2n)2+(9mn)﹣2+(3m)2014n2016的值.
21.已知.三角形的底边长为(2x+1)cm,高是(x﹣2)cm,若把底边和高各增加5厘米,那么三角形面积增加了多少?并求出x=3时三角形增加的面积.
22、如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为a米的道路.(a>0,b>0)
(1)①试用含a,b的代数式表示绿化的面积是多少平方米?
②假设阴影部分可以拼成一个矩形,请你求出所拼矩形相邻两边的长;如果要使所拼矩形面积最大,求a与b满足的关系式;
(2)若a=3,b=2,请求出绿化面积.
1.B 2.C 3.D 4.D 5.B 6.A 7.B 8.C 9.D 10.C
11.答案为:x2+5x+6.
12.答案为:-5
13.答案为:x=-11/14;
14.答案为:0
15、一个长方体的长、宽、高分别是(3x﹣4)米,2x米和x米,则这个长方体的体积是 .
解:由题意可得,这个长方体的体积是(3x﹣4)×2x×x=(3x﹣4)×2x2=(6x3﹣8x2)立方米.
故答案为:(6x3﹣8x2)立方米.
16、如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要 张C类卡片.
解:∵(3a+b)(a+2b)=3a2+6ab+ab+2b2=3a2+7ab+2b2,
∴若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要A类3张,B类2张,C类7张.
故答案为:7.
三、解答题
17、计算:
解:(1)原式=2a2+5a﹣42﹣2a2+3a+2=8a﹣40.
(2)原式
(3)原式
18、先化简,再求值.,其中a,b满足.
解:∵,∴a-2=0,1-b=0,∴a=2,b=1,
∴原式=
=
=
∴当a=2,b=1时,原式=.
19.【答案】 (1)解:原式=2ax+bx+2ay+by
(2)解:原式=a2﹣b2
(3)解:原式=a2﹣ a﹣ab+ b
(4)解:原式=6x2﹣9xy﹣4xy+6y2=6x2﹣13xy+6y2
(5)解:原式=﹣3x2﹣6x﹣2x﹣4=﹣3x2﹣8x﹣4
20.【答案】 解:(x2+3mx﹣)(x2﹣3x+n)=x4nx2+(3m﹣3)x3﹣9mx2+(3mn+1)x﹣x2﹣n,
由积中不含x和x3项,得到3m﹣3=0,3mn+1=0,
解得:m=1,n=﹣ ,
(1)原式=(m﹣n)2=()2=;
(2)原式=324m4n2++(3mn)2014 n2=36++=36 .
21.【答案】解:根据题意,面积增加 (2x+1+5)(x﹣2+5)﹣ (2x+1)(x﹣2) = (2x2+6x+6x+18)﹣ (2x2﹣4x+x﹣2)
=x2+6x+9﹣(x2﹣ x﹣1)
= x+10,
当x=3时,原式= ×3+10=32.5(cm2).
22、如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为a米的道路.(a>0,b>0)
(1)①试用含a,b的代数式表示绿化的面积是多少平方米?
②假设阴影部分可以拼成一个矩形,请你求出所拼矩形相邻两边的长;如果要使所拼矩形面积最大,求a与b满足的关系式;
(2)若a=3,b=2,请求出绿化面积.
解:(1)①绿化的面积为:(3a+b)(2a+b)﹣(a+b)2﹣a(3a+b﹣a﹣b)
=6a2+5ab+b2﹣a2﹣2ab﹣b2﹣2a2
=(3a2+3ab)平方米;
答:绿化的面积是(3a2+3ab)平方米;
②如图,∵3a2+3ab=3a(a+b),
∴所拼矩形相邻两边的长分别为3a米和(a+b)米;
所以要使所拼矩形面积最大,3a=a+b,所以2a=b;
(2)当a=3,b=2,
绿化面积是3a2+3ab=3×9+3×3×2=45(平方米).
一、选择题
1、计算(2m+3)(m﹣1)的结果是( )
A.2m2﹣m﹣3 B.2m2+m﹣3 C.2m2﹣m+3 D.m2﹣m﹣3
2.(2020·浙江杭州市·七年级期中)若a,b,k均为整数,则满足等式的所有k值的个数为( )
A.2个 B.4个 C.6个 D.8个
3如果展开后结果中不含的一次项,则等于
A. B. C. D.
4已知,是常数,若化简的结果不含的二次项,则的值为
A. B. C. D.
5、当x=1时,ax+b+1的值为﹣3,则(a+b﹣1)(3﹣2a﹣2b)的值为( )
A.55 B.﹣55 C.25 D.﹣25
6、若M=(x﹣3)(x﹣4),N=(x﹣1)(x﹣6),则M与N的大小关系为( )
A.M>N B.M=N C.M<N D.由 x 的取值而定
7、如图,在一块长为a米,宽为b米的长方形草地上,有一条弯曲的小路,小路的左边线向右平移2米就是它的右边线,这块草地的绿地面积是(单位:平方米)( )
A.ab B.(a﹣2)b C.a(b﹣2) D.(a﹣2)(b﹣2)
8、如图,现有正方形卡片A类,B类和长方形卡片C类若干张,如果要拼一个长为(a+3b),宽为(a+2b)的大长方形,则需要C类卡片( )
A.3张 B.4张 C.5张 D.6张
9、如图,若用两种方法表示图中阴影部分的面积,则可以得到的代数恒等式是( )
A.(m+a)(m﹣b)=m2+(a﹣b)m﹣ab B.(m﹣a)(m+b)=m2+(b﹣a)m﹣ab
C.(m﹣a)(m﹣b)=m2﹣(a﹣b)m+ab D.(m﹣a)(m﹣b)=m2﹣(a+b)m+ab
10、根据图1的面积可以说明多项式的乘法运算(2a+b)(a+b)=2a2+3ab+b2,那么根据图2的面积可以说明多项式的乘法运算是( )
A.(a+3b)(a+b)=a2+4ab+3b2 B.(a+3b)(a+b)=a2+3b2
C.(b+3a)(b+a)=b2+4ab+3a2 D.(a+3b)(a﹣b)=a2+2ab﹣3b2
二、填空题
11.如图,矩形ABCD的面积为 (用含x的代数式表示).
12.如果(x-2)(x+3)=x2+px+q,那么p+q的值为 .
13.方程(x+3)(2x-5)-(2x+1)(x-8)=41的解是_______.
14.已知(x-1)(x+2)=ax2+bx+c,则代数式4a-2b+c的值为 .
15、一个长方体的长、宽、高分别是(3x﹣4)米,2x米和x米,则这个长方体的体积是 .
16、如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要 张C类卡片.
三、解答题
17、计算:
(1)(2a﹣7)(a+6)﹣(a﹣2)(2a+1)
(2)
(3)
18、先化简,再求值.,其中a,b满足.
19.计算.
(1)(x+y)(2a+b);
(2)(a+b)(a﹣b);
(3) ;
(4)(3x﹣2y)(2x﹣3y);
(5)(3x+2)(﹣x﹣2).
20.若(x2+3mx﹣)(x2﹣3x+n)的积中不含x和x3项,
(1)求m2﹣mn+n2的值;
(2)求代数式(﹣18m2n)2+(9mn)﹣2+(3m)2014n2016的值.
21.已知.三角形的底边长为(2x+1)cm,高是(x﹣2)cm,若把底边和高各增加5厘米,那么三角形面积增加了多少?并求出x=3时三角形增加的面积.
22、如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为a米的道路.(a>0,b>0)
(1)①试用含a,b的代数式表示绿化的面积是多少平方米?
②假设阴影部分可以拼成一个矩形,请你求出所拼矩形相邻两边的长;如果要使所拼矩形面积最大,求a与b满足的关系式;
(2)若a=3,b=2,请求出绿化面积.
1.B 2.C 3.D 4.D 5.B 6.A 7.B 8.C 9.D 10.C
11.答案为:x2+5x+6.
12.答案为:-5
13.答案为:x=-11/14;
14.答案为:0
15、一个长方体的长、宽、高分别是(3x﹣4)米,2x米和x米,则这个长方体的体积是 .
解:由题意可得,这个长方体的体积是(3x﹣4)×2x×x=(3x﹣4)×2x2=(6x3﹣8x2)立方米.
故答案为:(6x3﹣8x2)立方米.
16、如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要 张C类卡片.
解:∵(3a+b)(a+2b)=3a2+6ab+ab+2b2=3a2+7ab+2b2,
∴若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要A类3张,B类2张,C类7张.
故答案为:7.
三、解答题
17、计算:
解:(1)原式=2a2+5a﹣42﹣2a2+3a+2=8a﹣40.
(2)原式
(3)原式
18、先化简,再求值.,其中a,b满足.
解:∵,∴a-2=0,1-b=0,∴a=2,b=1,
∴原式=
=
=
∴当a=2,b=1时,原式=.
19.【答案】 (1)解:原式=2ax+bx+2ay+by
(2)解:原式=a2﹣b2
(3)解:原式=a2﹣ a﹣ab+ b
(4)解:原式=6x2﹣9xy﹣4xy+6y2=6x2﹣13xy+6y2
(5)解:原式=﹣3x2﹣6x﹣2x﹣4=﹣3x2﹣8x﹣4
20.【答案】 解:(x2+3mx﹣)(x2﹣3x+n)=x4nx2+(3m﹣3)x3﹣9mx2+(3mn+1)x﹣x2﹣n,
由积中不含x和x3项,得到3m﹣3=0,3mn+1=0,
解得:m=1,n=﹣ ,
(1)原式=(m﹣n)2=()2=;
(2)原式=324m4n2++(3mn)2014 n2=36++=36 .
21.【答案】解:根据题意,面积增加 (2x+1+5)(x﹣2+5)﹣ (2x+1)(x﹣2) = (2x2+6x+6x+18)﹣ (2x2﹣4x+x﹣2)
=x2+6x+9﹣(x2﹣ x﹣1)
= x+10,
当x=3时,原式= ×3+10=32.5(cm2).
22、如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为a米的道路.(a>0,b>0)
(1)①试用含a,b的代数式表示绿化的面积是多少平方米?
②假设阴影部分可以拼成一个矩形,请你求出所拼矩形相邻两边的长;如果要使所拼矩形面积最大,求a与b满足的关系式;
(2)若a=3,b=2,请求出绿化面积.
解:(1)①绿化的面积为:(3a+b)(2a+b)﹣(a+b)2﹣a(3a+b﹣a﹣b)
=6a2+5ab+b2﹣a2﹣2ab﹣b2﹣2a2
=(3a2+3ab)平方米;
答:绿化的面积是(3a2+3ab)平方米;
②如图,∵3a2+3ab=3a(a+b),
∴所拼矩形相邻两边的长分别为3a米和(a+b)米;
所以要使所拼矩形面积最大,3a=a+b,所以2a=b;
(2)当a=3,b=2,
绿化面积是3a2+3ab=3×9+3×3×2=45(平方米).
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
