人教版八年级数学下册 16.2.1 二次根式的乘法 课件(共23张PPT)
文档属性
| 名称 | 人教版八年级数学下册 16.2.1 二次根式的乘法 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 15:49:41 | ||
图片预览








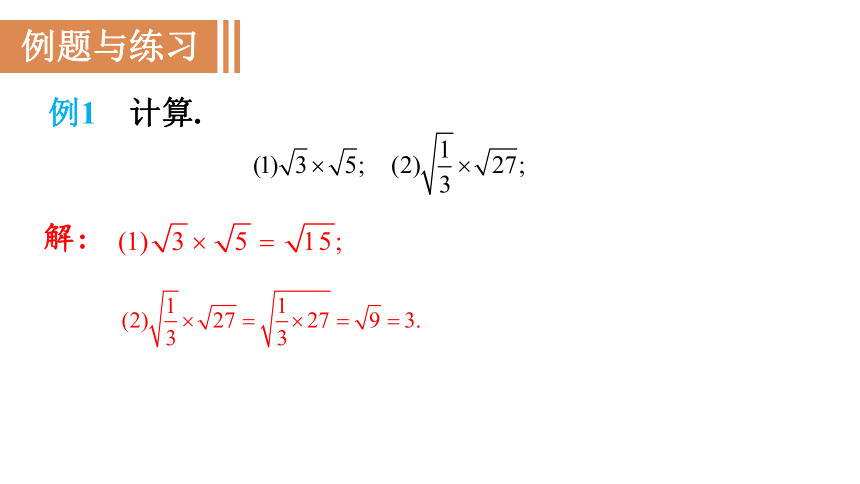
文档简介
(共23张PPT)
第十六章 二次根式
16.2 二次根式的乘除
第1课时 二次根式的乘法
导入新课
1.回顾二次根式的性质和算术平方根的概念.
( )2(a≥0)的性质:
即一个非负数的算术平方根的平方等于它本身.
的性质:
a (a≥0)
-a (a<0)
即任意一个数的平方的算术平方根等于它本身的绝对值.
如果 x2 = a(x≥0),那么 x 称为 a 的算术平方根.
用 表示.
算术平方根的概念
2.下列运算正确的是( )
A
3.计算:
10
10
12
12
思考: 与 的结果相同吗?你发现了什么?
探究新知
2×3=6
4×5=20
5×6=30
计算下列各式:
探究
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
思考 你发现了什么规律?你能用字母表示你所发现的规律吗?
猜测:
你能证明这个猜测吗?
求证:
证明:根据积的乘方法则,有
∴
就是ab的算术平方根.
又∵ 表示ab的算术平方根,
∴ .
知识归纳
一般地,对于二次根式的乘法是
语言表述:算术平方根的积等于各个被开方数积的算术平方根.
二次根式的乘法法则:
二次根式相乘,__________不变,____________相乘.
根指数
被开方数
注意:a,b都必须是非负数.
在本章中,如果没有特别说明,所有的字母都表示正数.
例题与练习
解:
例1 计算.
例2 化简
解:(1) ;
(1) ;(2) .
(2)
4a2b3含有像4,a2,b2,这样开的尽方的因数或因式,把它们开方后移到根号外.
归纳
反过来:
(a≥0,b≥0)
(a≥0,b≥0)
一般的:
这个性质在有的地方称之为“积的算术平方根的性质”
我们可以运用它来进行二次根式的解题和化简.
语言表述:积的算术平方根,等于积中各因式的算术平方根的积.
例3 计算.
(1)
解:(1)
(2)
(3)
(2)
(3)
当二次根式根号外的因数不为1时,可类比单项式乘单项
式的法则计算,即 .
归纳
二次根式的乘法法则的推广:
①多个二次根式相乘时此法则也适用,即
②当二次根号外有因数(式)时,可以类比单项式乘单项式的法则计算,即根号外的因数(式)的积作为根号外的因数(式),被开方数的积作为被开方数,即
归纳
化简二次根式的步骤:
1.把被开方数分解因式(或因数) ;
2.把各因式(或因数)积的算术平方根化为每个因式(或因数)的算术平方根的积;
3.如果因式中有平方式(或平方数),应用关系式
把这个因式(或因数)开出来,将二次根式化简 .
归纳
例4 计算:
化简时根号外的因数可先相乘:
例5 比较 与 的大小.
解:方法一:
方法二:
比较两个二次根式大小的方法:
(1)被开方数比较法,即先将根号外的非负因数移到根号内,当两个二次根式都是正数时,被开方数大的二次根式大.
(2)平方法,即把两个二次根式分别平方,当两个二次根式都是正数时,平方大的二次根式大.
(3)计算器求近似值法,即先利用计算器求出两个二次根式的近似值,再进行比较.
方
法
点
拨
1.计算:
例题与练习
2.化简
2
-36
3.一个长方形的长和宽分别是 ,求这个长方形的面积.
=
6.计算:
7.一个底面为30 cm×30 cm的长方体玻璃容器中装满水,现将一部分水倒入一个底面为正方形、高为10 cm的长方体铁桶中,当铁桶装满水时,容器中的水面下降了20 cm,铁桶的底面边长是多少厘米?
解:设铁桶的底面边长是 x cm.
由题意,得x2×10=30×30×20,x2=30×30×2,
答:铁桶的底面边长是 cm.
课堂小结
二次根式乘法
法则
性质
拓展
法则
第十六章 二次根式
16.2 二次根式的乘除
第1课时 二次根式的乘法
导入新课
1.回顾二次根式的性质和算术平方根的概念.
( )2(a≥0)的性质:
即一个非负数的算术平方根的平方等于它本身.
的性质:
a (a≥0)
-a (a<0)
即任意一个数的平方的算术平方根等于它本身的绝对值.
如果 x2 = a(x≥0),那么 x 称为 a 的算术平方根.
用 表示.
算术平方根的概念
2.下列运算正确的是( )
A
3.计算:
10
10
12
12
思考: 与 的结果相同吗?你发现了什么?
探究新知
2×3=6
4×5=20
5×6=30
计算下列各式:
探究
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
思考 你发现了什么规律?你能用字母表示你所发现的规律吗?
猜测:
你能证明这个猜测吗?
求证:
证明:根据积的乘方法则,有
∴
就是ab的算术平方根.
又∵ 表示ab的算术平方根,
∴ .
知识归纳
一般地,对于二次根式的乘法是
语言表述:算术平方根的积等于各个被开方数积的算术平方根.
二次根式的乘法法则:
二次根式相乘,__________不变,____________相乘.
根指数
被开方数
注意:a,b都必须是非负数.
在本章中,如果没有特别说明,所有的字母都表示正数.
例题与练习
解:
例1 计算.
例2 化简
解:(1) ;
(1) ;(2) .
(2)
4a2b3含有像4,a2,b2,这样开的尽方的因数或因式,把它们开方后移到根号外.
归纳
反过来:
(a≥0,b≥0)
(a≥0,b≥0)
一般的:
这个性质在有的地方称之为“积的算术平方根的性质”
我们可以运用它来进行二次根式的解题和化简.
语言表述:积的算术平方根,等于积中各因式的算术平方根的积.
例3 计算.
(1)
解:(1)
(2)
(3)
(2)
(3)
当二次根式根号外的因数不为1时,可类比单项式乘单项
式的法则计算,即 .
归纳
二次根式的乘法法则的推广:
①多个二次根式相乘时此法则也适用,即
②当二次根号外有因数(式)时,可以类比单项式乘单项式的法则计算,即根号外的因数(式)的积作为根号外的因数(式),被开方数的积作为被开方数,即
归纳
化简二次根式的步骤:
1.把被开方数分解因式(或因数) ;
2.把各因式(或因数)积的算术平方根化为每个因式(或因数)的算术平方根的积;
3.如果因式中有平方式(或平方数),应用关系式
把这个因式(或因数)开出来,将二次根式化简 .
归纳
例4 计算:
化简时根号外的因数可先相乘:
例5 比较 与 的大小.
解:方法一:
方法二:
比较两个二次根式大小的方法:
(1)被开方数比较法,即先将根号外的非负因数移到根号内,当两个二次根式都是正数时,被开方数大的二次根式大.
(2)平方法,即把两个二次根式分别平方,当两个二次根式都是正数时,平方大的二次根式大.
(3)计算器求近似值法,即先利用计算器求出两个二次根式的近似值,再进行比较.
方
法
点
拨
1.计算:
例题与练习
2.化简
2
-36
3.一个长方形的长和宽分别是 ,求这个长方形的面积.
=
6.计算:
7.一个底面为30 cm×30 cm的长方体玻璃容器中装满水,现将一部分水倒入一个底面为正方形、高为10 cm的长方体铁桶中,当铁桶装满水时,容器中的水面下降了20 cm,铁桶的底面边长是多少厘米?
解:设铁桶的底面边长是 x cm.
由题意,得x2×10=30×30×20,x2=30×30×2,
答:铁桶的底面边长是 cm.
课堂小结
二次根式乘法
法则
性质
拓展
法则
