人教版八年级数学下册 17.1.1 勾股定理 课件 (共24张PPT)
文档属性
| 名称 | 人教版八年级数学下册 17.1.1 勾股定理 课件 (共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 16:24:39 | ||
图片预览


文档简介
(共24张PPT)
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理
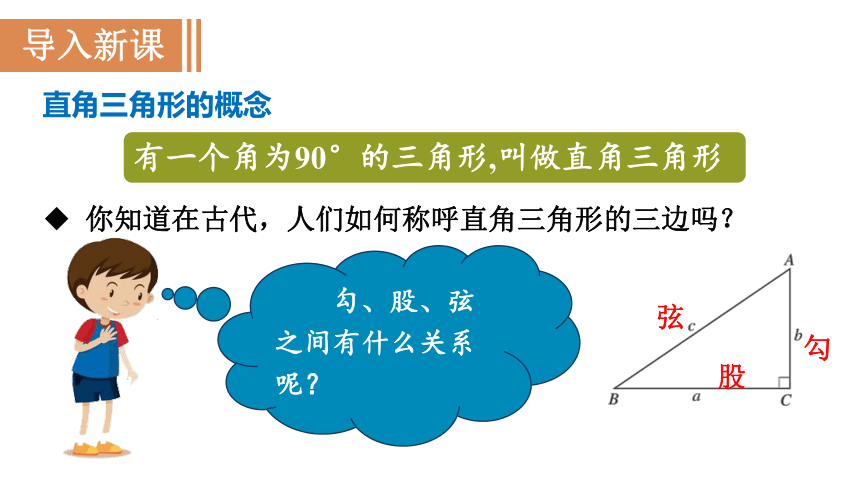
导入新课
有一个角为90°的三角形,叫做直角三角形
直角三角形的概念
你知道在古代,人们如何称呼直角三角形的三边吗?
勾
股
弦
勾、股、弦之间有什么关系呢?
探究新知
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用等腰三角形砖铺成的地面(如图):
你从图片中发现了什么?
观察
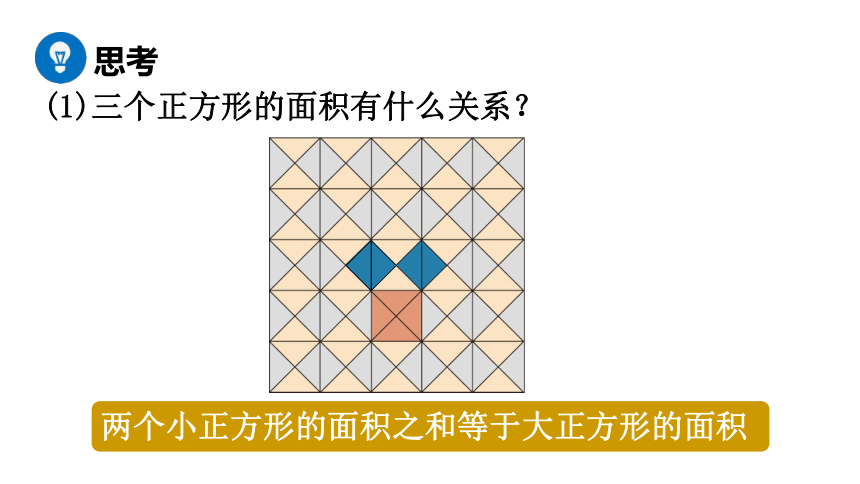
(1)三个正方形的面积有什么关系?
两个小正方形的面积之和等于大正方形的面积
思考
S
S1
S2
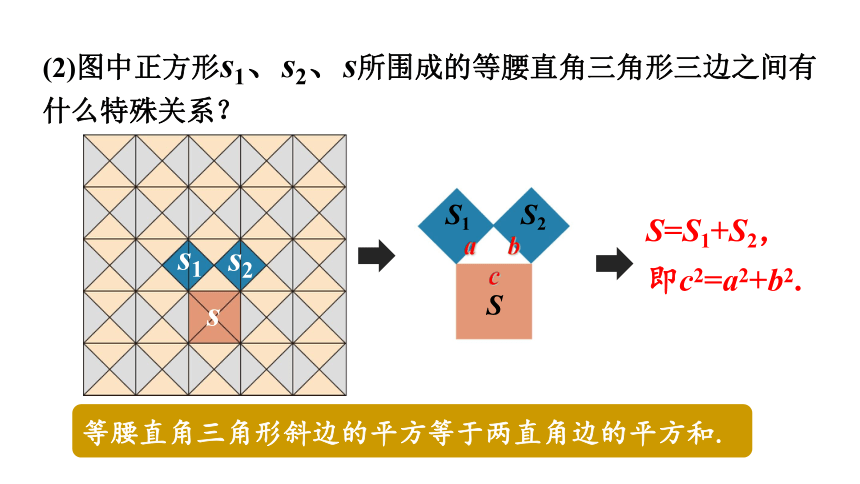
等腰直角三角形斜边的平方等于两直角边的平方和.
S=S1+S2,
a b
c
(2)图中正方形s1、s2、s所围成的等腰直角三角形三边之间有什么特殊关系?
s1
s2
s
即c2=a2+b2.
探究
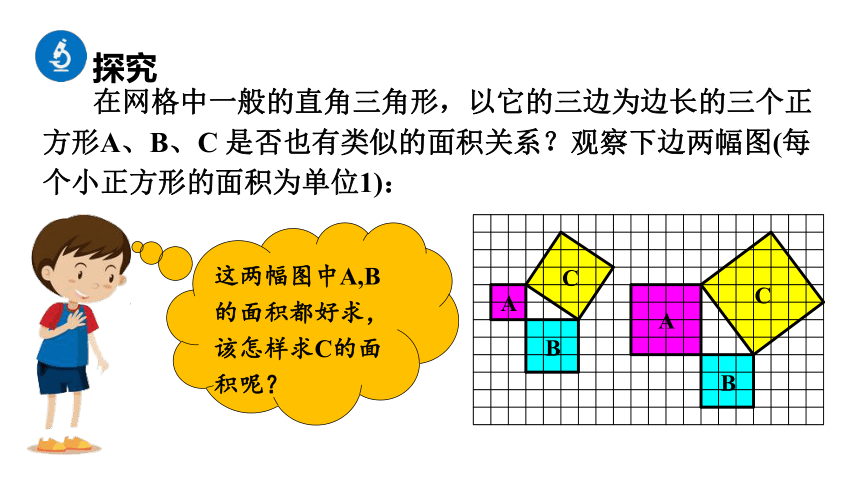
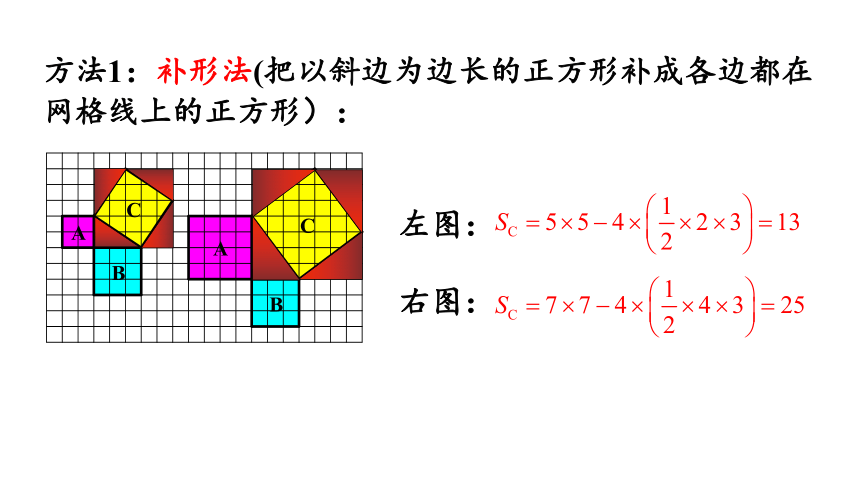
在网格中一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
这两幅图中A,B的面积都好求,该怎样求C的面积呢?
方法1:补形法(把以斜边为边长的正方形补成各边都在网格线上的正方形):
左图:
右图:
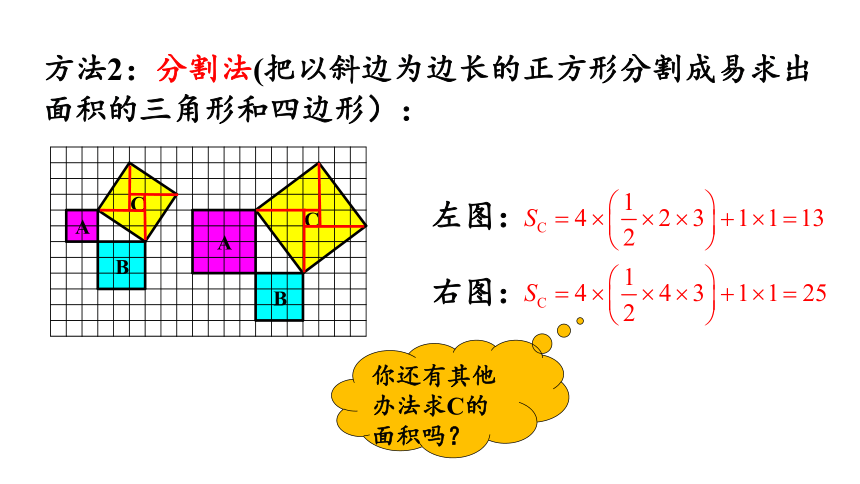
方法2:分割法(把以斜边为边长的正方形分割成易求出面积的三角形和四边形):
左图:
右图:
你还有其他办法求C的面积吗?
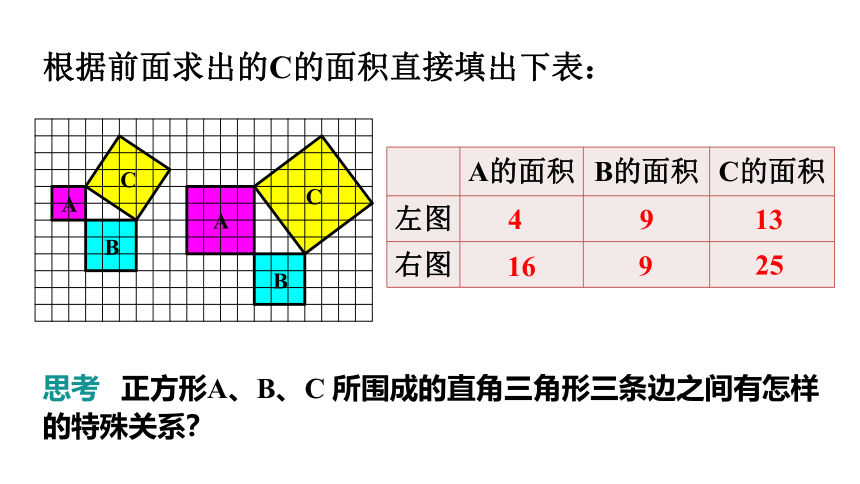
根据前面求出的C的面积直接填出下表:
A的面积 B的面积 C的面积
左图
右图
4
13
25
9
16
9
思考 正方形A、B、C 所围成的直角三角形三条边之间有怎样的特殊关系?
知识归纳
命题1 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
由上面的几个例子,我们猜想:
a
b
c
思考 你能用不同的方式证明命题1吗?
a
b
b
c
a
b
c
a
证法1 让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
a
b
c
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
∵S大正方形=c2,
S小正方形=(b-a)2,
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因此,这个图案被选为2002年在北京召开的国际数学家大会的会徽.
证法2 毕达哥拉斯证法,请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
证明:
S大正方形=4S直角三角形+ S小正方形
=4× ab+c2
=c2+2ab,
∵S大正方形=(a+b)2=a2+b2+2ab,
a
a
b
b
c
c
∴a2 + b2 = c2.
证法3 美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
公式变形
( a、b、c为正数)
勾股定理
a
b
c
知识归纳
练习
1.设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
解:由勾股定理得52+122=c2 ,c=13;
解:由勾股定理得62+b2=102, b=8;
解:由勾股定理得a2+152=252 ,a=20.
2.如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.
解:根据图形正方形E 的边长为:
故E的面积为:252=625.
例题与练习
例1 在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)若a= ,c=4,求b;
(2)若c=8,∠A=30°,求b;
(3)若a∶b=3∶4,c=15,求S△ABC.
解:(1)b=3;
(2)b= ;
(3)S△ABC=54.
例2 如图,在△ABC中,AD⊥BC于点D,AB=3,BD=2,DC=1,求AC的长.
解:∵AD⊥BC,
∴在Rt△ADC中,
∴∠ADB=∠ADC=90°.
在Rt△ABD中,
例3 如图,四边形ABCD是长方形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.
解:由折叠的性质,得△ACD≌△ACD′,
∴∠D′=∠D=90°,CD′=CD=AB=3.
∵∠AEB=∠CED′,∠B=∠D′=90°,
∴△ABE≌△CD′E(AAS),
设BE=x,则AE=CE=4-x.
在Rt△ABE中,由勾股定理,得AE2=AB2+BE2,
即(4-x)2=32+x2,
∴AE=CE.
练习
1.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60
C.76 D.80
C
2.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且a+b= ,c=3,求△ABC的面积.
∴a2+b2+2ab=12.由题知,a2+b2=c2=9,
解:∵a+b= ,
课堂小结
勾股定理
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
证明
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理
导入新课
有一个角为90°的三角形,叫做直角三角形
直角三角形的概念
你知道在古代,人们如何称呼直角三角形的三边吗?
勾
股
弦
勾、股、弦之间有什么关系呢?
探究新知
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用等腰三角形砖铺成的地面(如图):
你从图片中发现了什么?
观察
(1)三个正方形的面积有什么关系?
两个小正方形的面积之和等于大正方形的面积
思考
S
S1
S2
等腰直角三角形斜边的平方等于两直角边的平方和.
S=S1+S2,
a b
c
(2)图中正方形s1、s2、s所围成的等腰直角三角形三边之间有什么特殊关系?
s1
s2
s
即c2=a2+b2.
探究
在网格中一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
这两幅图中A,B的面积都好求,该怎样求C的面积呢?
方法1:补形法(把以斜边为边长的正方形补成各边都在网格线上的正方形):
左图:
右图:
方法2:分割法(把以斜边为边长的正方形分割成易求出面积的三角形和四边形):
左图:
右图:
你还有其他办法求C的面积吗?
根据前面求出的C的面积直接填出下表:
A的面积 B的面积 C的面积
左图
右图
4
13
25
9
16
9
思考 正方形A、B、C 所围成的直角三角形三条边之间有怎样的特殊关系?
知识归纳
命题1 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
由上面的几个例子,我们猜想:
a
b
c
思考 你能用不同的方式证明命题1吗?
a
b
b
c
a
b
c
a
证法1 让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
a
b
c
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
∵S大正方形=c2,
S小正方形=(b-a)2,
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因此,这个图案被选为2002年在北京召开的国际数学家大会的会徽.
证法2 毕达哥拉斯证法,请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
证明:
S大正方形=4S直角三角形+ S小正方形
=4× ab+c2
=c2+2ab,
∵S大正方形=(a+b)2=a2+b2+2ab,
a
a
b
b
c
c
∴a2 + b2 = c2.
证法3 美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
公式变形
( a、b、c为正数)
勾股定理
a
b
c
知识归纳
练习
1.设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
解:由勾股定理得52+122=c2 ,c=13;
解:由勾股定理得62+b2=102, b=8;
解:由勾股定理得a2+152=252 ,a=20.
2.如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.
解:根据图形正方形E 的边长为:
故E的面积为:252=625.
例题与练习
例1 在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)若a= ,c=4,求b;
(2)若c=8,∠A=30°,求b;
(3)若a∶b=3∶4,c=15,求S△ABC.
解:(1)b=3;
(2)b= ;
(3)S△ABC=54.
例2 如图,在△ABC中,AD⊥BC于点D,AB=3,BD=2,DC=1,求AC的长.
解:∵AD⊥BC,
∴在Rt△ADC中,
∴∠ADB=∠ADC=90°.
在Rt△ABD中,
例3 如图,四边形ABCD是长方形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.
解:由折叠的性质,得△ACD≌△ACD′,
∴∠D′=∠D=90°,CD′=CD=AB=3.
∵∠AEB=∠CED′,∠B=∠D′=90°,
∴△ABE≌△CD′E(AAS),
设BE=x,则AE=CE=4-x.
在Rt△ABE中,由勾股定理,得AE2=AB2+BE2,
即(4-x)2=32+x2,
∴AE=CE.
练习
1.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60
C.76 D.80
C
2.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,且a+b= ,c=3,求△ABC的面积.
∴a2+b2+2ab=12.由题知,a2+b2=c2=9,
解:∵a+b= ,
课堂小结
勾股定理
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
证明
