人教版八年级数学下册 17.1.3 利用勾股定理作图 课件 (共20张PPT)
文档属性
| 名称 | 人教版八年级数学下册 17.1.3 利用勾股定理作图 课件 (共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 16:27:47 | ||
图片预览





文档简介
(共20张PPT)
第十七章 勾股定理
17.1 勾股定理
第3课时 利用勾股定理作图
导入新课
欣赏下面海螺的图片:
在数学中也有这样一幅美丽的“海螺型”图案,如第七届国际数学教育大会的会徽.
这个图是怎样绘制出来的呢?
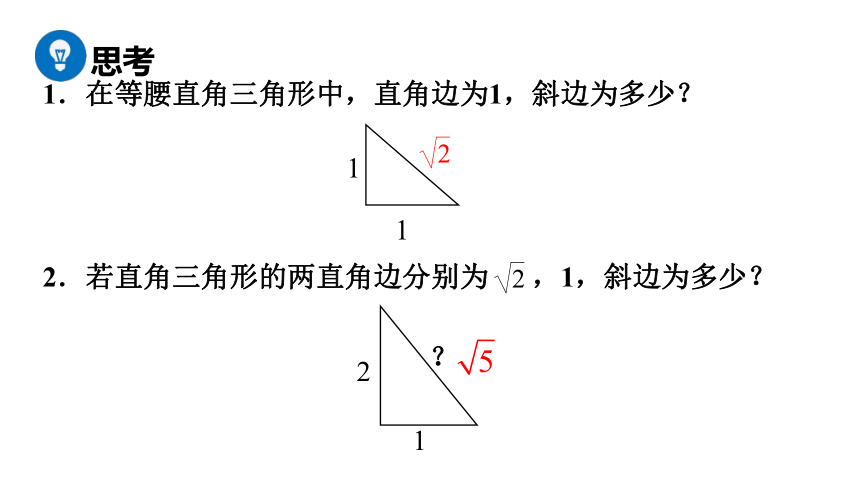
1.在等腰直角三角形中,直角边为1,斜边为多少?
2
1
?
2.若直角三角形的两直角边分别为 ,1,斜边为多少?
1
1
思考
-1 0 1 2 3
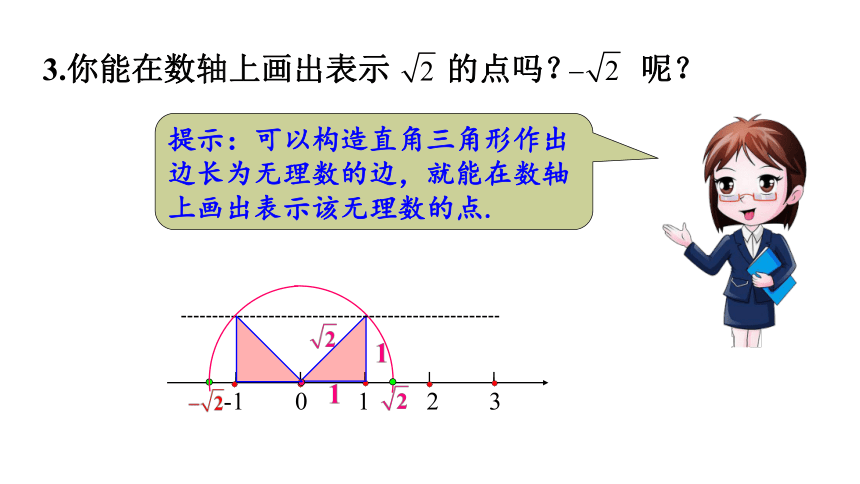
3.你能在数轴上画出表示 的点吗? 呢?
提示:可以构造直角三角形作出边长为无理数的边,就能在数轴上画出表示该无理数的点.
探究新知
思考
在八年级上册中我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
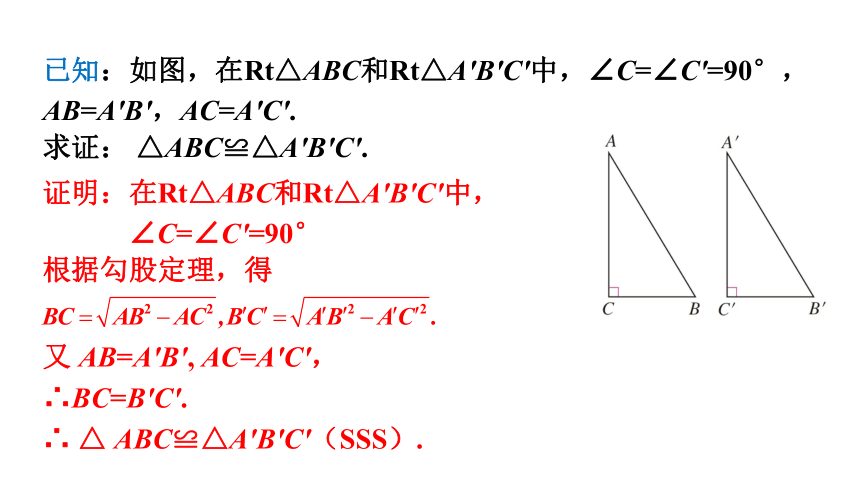
已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,AB=A′B′,AC=A′C′.
求证: △ABC≌△A′B′C′.
证明:在Rt△ABC和Rt△A′B′C′中,
∠C=∠C′=90°
又 AB=A′B′, AC=A′C′,
根据勾股定理,得
∴BC=B′C′.
∴ △ ABC≌△A′B′C′(SSS).
探究
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
分析:13开方就是 ,如果一个三角形的斜边长为 的话,问题就可迎刃而解了.
是直角边分别为2,3的直角三角形的斜边长.
√
√
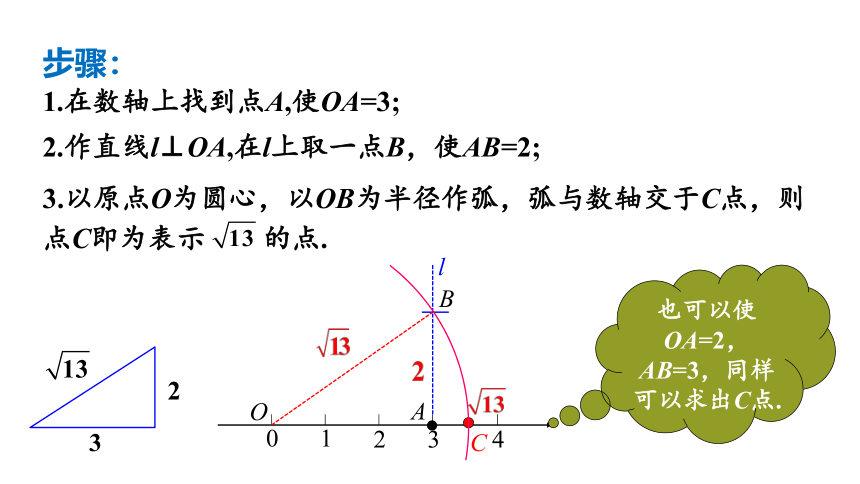
步骤:
0
1
2
3
4
l
A
B
C
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点.
O
也可以使OA=2,AB=3,同样可以求出C点.
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
知识归纳
类似地,利用勾股定理可以作出长为 线段.
探究新知
“数学海螺”
1
1
-1 0 1 2 3
例题与练习
0
1
2
3
4
l
A
B
C
作法:
(1)在数轴上找到点A,使OA=1;
例1 在数轴上作出表示 的点.
(2)过点A作直线垂直于OA,在直线上取点B, 使AB=4,那么OB= ;
(3)以原点O为圆心,以OB为半径作弧,弧与数轴交于点C,则OC= .
如图,在数轴上,点C为表示 的点.
练习
1.在数轴上作出表示 的点.
∴ 是以4,1为直角边的直角三角形斜边的长,
-3 -2 -1 0 1
-4
-5
C
如图,即点C表示 .
2.如图,等边三角形的边长是6.求:
(1)高AD的长;
(2)这个三角形的面积.
解:(1)AD⊥BC于D,则BD=CD=3.
(2)S= ·BC·AD= ×6×3 ≈15.6
在Rt△ABD中,由勾股定理
AD2=AB2-BD2=62-32=27,故AD=3 ≈5.2
例2 利用如图4×4的方格,作出面积为8平方单位的正方形,然后在数轴上表示实数 和 .
解:如图.
0
1
2
3
4
-4
-3
-2
-1
例3 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫格点.
(1)在图①中以格点为顶点画一个面积为5的正方形;
图①
解:如图①所示;
(2)如图②,A,B,C是小正方形的顶点,求∠ABC的度数.
解:如图②,连接AC,并设点D,E,
∴∠ABC=45°.
则BC=AC= ,且易证△ACD≌△BCE,
∴∠ACD=∠BCE,
∴∠ACD+∠DCB=∠BCE+∠DCB,
即∠ACB=∠DCE=90°,
A
C
B
E
D
图②
练习
3.小明学了利用勾股定理在数轴上找一个无理数的准确位置后,又进一步进行练习:首先画出数轴,设原点为点O,数轴上的2处表示点A,然后过点A作AB⊥OA,且AB=3.以点O为圆心,OB为半径作弧,设与数轴右侧交点为P,则点P的位置在数轴上( )
A.1和2之间 B.2和3之间
C.3和4之间 D.4和5之间
C
4.如图,在矩形ABCD中,BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上的点F处,则DE的长是_______.
5
5.在平静的湖面上,有一棵水草,它高出水面3 dm,一阵风吹来,水草被吹到一边,草尖齐至水面,已知水草移动的水平距离为6 dm,问这里的水深是多少?
解:根据题意,作图(如图).
A
C
D
B
其中D是无风时水草的最高点,BC为湖面,AB是一阵风吹过水草的位置,则CD=3 dm,CB=6 dm,AD=AB,BC⊥AD.
在Rt△ACB中,AB2=AC2+BC2,
即(AC+3)2=AC2+62,
解得AC=4.5.
课堂小结
勾股定理的逆定理的应用
应用
航海问题
方法
认真审题,画出符合题意的图形,熟练运用勾股定理及其逆
定理来解决问题
与勾股定理结合解决不规则图形等问题
第十七章 勾股定理
17.1 勾股定理
第3课时 利用勾股定理作图
导入新课
欣赏下面海螺的图片:
在数学中也有这样一幅美丽的“海螺型”图案,如第七届国际数学教育大会的会徽.
这个图是怎样绘制出来的呢?
1.在等腰直角三角形中,直角边为1,斜边为多少?
2
1
?
2.若直角三角形的两直角边分别为 ,1,斜边为多少?
1
1
思考
-1 0 1 2 3
3.你能在数轴上画出表示 的点吗? 呢?
提示:可以构造直角三角形作出边长为无理数的边,就能在数轴上画出表示该无理数的点.
探究新知
思考
在八年级上册中我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,AB=A′B′,AC=A′C′.
求证: △ABC≌△A′B′C′.
证明:在Rt△ABC和Rt△A′B′C′中,
∠C=∠C′=90°
又 AB=A′B′, AC=A′C′,
根据勾股定理,得
∴BC=B′C′.
∴ △ ABC≌△A′B′C′(SSS).
探究
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
分析:13开方就是 ,如果一个三角形的斜边长为 的话,问题就可迎刃而解了.
是直角边分别为2,3的直角三角形的斜边长.
√
√
步骤:
0
1
2
3
4
l
A
B
C
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点.
O
也可以使OA=2,AB=3,同样可以求出C点.
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
知识归纳
类似地,利用勾股定理可以作出长为 线段.
探究新知
“数学海螺”
1
1
-1 0 1 2 3
例题与练习
0
1
2
3
4
l
A
B
C
作法:
(1)在数轴上找到点A,使OA=1;
例1 在数轴上作出表示 的点.
(2)过点A作直线垂直于OA,在直线上取点B, 使AB=4,那么OB= ;
(3)以原点O为圆心,以OB为半径作弧,弧与数轴交于点C,则OC= .
如图,在数轴上,点C为表示 的点.
练习
1.在数轴上作出表示 的点.
∴ 是以4,1为直角边的直角三角形斜边的长,
-3 -2 -1 0 1
-4
-5
C
如图,即点C表示 .
2.如图,等边三角形的边长是6.求:
(1)高AD的长;
(2)这个三角形的面积.
解:(1)AD⊥BC于D,则BD=CD=3.
(2)S= ·BC·AD= ×6×3 ≈15.6
在Rt△ABD中,由勾股定理
AD2=AB2-BD2=62-32=27,故AD=3 ≈5.2
例2 利用如图4×4的方格,作出面积为8平方单位的正方形,然后在数轴上表示实数 和 .
解:如图.
0
1
2
3
4
-4
-3
-2
-1
例3 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫格点.
(1)在图①中以格点为顶点画一个面积为5的正方形;
图①
解:如图①所示;
(2)如图②,A,B,C是小正方形的顶点,求∠ABC的度数.
解:如图②,连接AC,并设点D,E,
∴∠ABC=45°.
则BC=AC= ,且易证△ACD≌△BCE,
∴∠ACD=∠BCE,
∴∠ACD+∠DCB=∠BCE+∠DCB,
即∠ACB=∠DCE=90°,
A
C
B
E
D
图②
练习
3.小明学了利用勾股定理在数轴上找一个无理数的准确位置后,又进一步进行练习:首先画出数轴,设原点为点O,数轴上的2处表示点A,然后过点A作AB⊥OA,且AB=3.以点O为圆心,OB为半径作弧,设与数轴右侧交点为P,则点P的位置在数轴上( )
A.1和2之间 B.2和3之间
C.3和4之间 D.4和5之间
C
4.如图,在矩形ABCD中,BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上的点F处,则DE的长是_______.
5
5.在平静的湖面上,有一棵水草,它高出水面3 dm,一阵风吹来,水草被吹到一边,草尖齐至水面,已知水草移动的水平距离为6 dm,问这里的水深是多少?
解:根据题意,作图(如图).
A
C
D
B
其中D是无风时水草的最高点,BC为湖面,AB是一阵风吹过水草的位置,则CD=3 dm,CB=6 dm,AD=AB,BC⊥AD.
在Rt△ACB中,AB2=AC2+BC2,
即(AC+3)2=AC2+62,
解得AC=4.5.
课堂小结
勾股定理的逆定理的应用
应用
航海问题
方法
认真审题,画出符合题意的图形,熟练运用勾股定理及其逆
定理来解决问题
与勾股定理结合解决不规则图形等问题
