人教版八年级数学下册 18.1.2.2平行四边形的判定2 课件(共13张PPT)
文档属性
| 名称 | 人教版八年级数学下册 18.1.2.2平行四边形的判定2 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 750.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 16:57:24 | ||
图片预览




文档简介
(共13张PPT)
第十八章 平行四边形
18 .1 平行四边形
18.1.2 平行四边形的判定
第2课时 平行四边形的判定(2)
导入新课
回顾上节课学行四边形有哪些判定定理?
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
探究新知
思考
我们知道,两组对边分别平行或相等的四边形是平行四边形,如果只考虑四边形的一组对边,他们满足什么条件时这个四边形能成为平行四边形呢?
猜想:一组对边平行且相等的四边形是平行四边形.
你能证明吗?
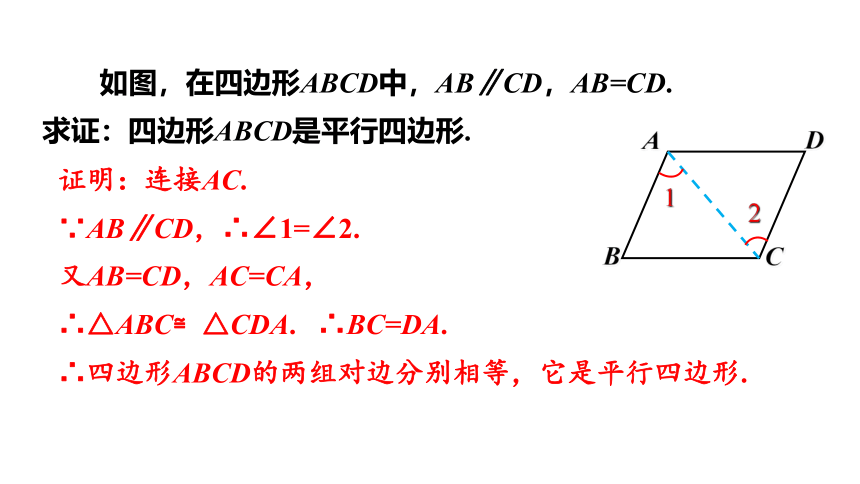
如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB∥CD,∴∠1=∠2.
又AB=CD,AC=CA,
∴△ABC≌△CDA. ∴BC=DA.
∴四边形ABCD的两组对边分别相等,它是平行四边形.
A
B
C
D
2
1
知识归纳
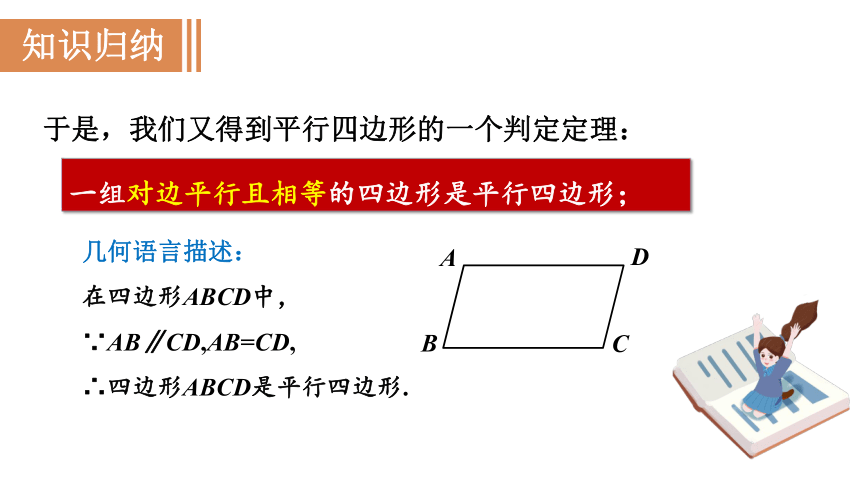
一组对边平行且相等的四边形是平行四边形;
于是,我们又得到平行四边形的一个判定定理:
几何语言描述:
在四边形ABCD中,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
B
D
A
C
证明:
∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
例1 教材P47例4.
探究新知
练习
1.为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了,你能说出其中的道理吗?
解:由一组对边平行且相等的四边形为平行四边形可知,两条直铺的铁轨互相平行.
2.如图,在平行四边形ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
求证:四边形AFCE是平行四边形.
证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∴∠ADE=∠CBF,
又∠AED=∠CFB=90°,∴△AED≌△CFB,
∴AE=CF.
又∵ ∠AEF=∠CFE=90°,
∴ AE∥CF,
∴四边形AFCE是平行四边形.
例2 如图,已知E,F是四边形ABCD对角线上两点,且AF=CE,DF=BE,DF∥BE,试说明四边形ABCD为平行四边形.
解:由AF=CE,得AE=CF.
又∵DF∥BE,
∴∠DFA=∠BEC,
∴∠DFC=∠BEA.
又∵DF=BE,
∴△CDF≌△ABE(SAS),
∴CD=AB,∠DCA=∠CAB,
例题与练习
∴CD∥AB,
∴四边形ABCD为平行四边形.
例3 如图,在四边形ABCD中,对角线AC与BD相交于点O,在①AB∥CD;②AO=CO;③AD=BC中任意选取两个作为条件,“四边形ABCD是平行四边形”作为结论构造命题.以①②作为条件构成的命题是真命题吗?若是,请证明;若不是,请举出反例.
解:以①②作为条件构成的命题是真命题.
证明如下:∵AB∥CD,
∴∠OAB=∠OCD.在△AOB和△COD中,
∴OB=OD.
∵OA=OC,
∴四边形ABCD是平行四边形.
∴△AOB≌△COD(ASA),
例题与练习
练习
1.在四边形中,有两条边相等,另外两边也相等,则这个四边形
( )
A.一定是平行四边形
B.一定不是平行四边形
C.可能是平行四边形,也可能不是平行四边形
D.上述答案都不对
C
2.如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6 cm,点P,Q分别从点A,C同时出发,点P以1 cm/s的速度由点A向点D运动,点Q以2 cm/s的速度由点C向点B运动,问几秒时,四边形ABQP是平行四边形?
解:设x s时,四边形ABQP是平行四边形.
根据题意,得AP=x,CQ=2x,
∴BQ=6-2x,
只有AP=BQ时,四边形ABQP才是平行四边形,
∴x=6-2x,解得x=2,
∴2 s时,四边形ABQP是平行四边形.
课堂小结
平行四边形的判定2
判定定理4
平行四边形的性质与判定的综合运用
一组对边平行且相等的四边形是平行四边形.
第十八章 平行四边形
18 .1 平行四边形
18.1.2 平行四边形的判定
第2课时 平行四边形的判定(2)
导入新课
回顾上节课学行四边形有哪些判定定理?
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
探究新知
思考
我们知道,两组对边分别平行或相等的四边形是平行四边形,如果只考虑四边形的一组对边,他们满足什么条件时这个四边形能成为平行四边形呢?
猜想:一组对边平行且相等的四边形是平行四边形.
你能证明吗?
如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB∥CD,∴∠1=∠2.
又AB=CD,AC=CA,
∴△ABC≌△CDA. ∴BC=DA.
∴四边形ABCD的两组对边分别相等,它是平行四边形.
A
B
C
D
2
1
知识归纳
一组对边平行且相等的四边形是平行四边形;
于是,我们又得到平行四边形的一个判定定理:
几何语言描述:
在四边形ABCD中,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
B
D
A
C
证明:
∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
例1 教材P47例4.
探究新知
练习
1.为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了,你能说出其中的道理吗?
解:由一组对边平行且相等的四边形为平行四边形可知,两条直铺的铁轨互相平行.
2.如图,在平行四边形ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
求证:四边形AFCE是平行四边形.
证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∴∠ADE=∠CBF,
又∠AED=∠CFB=90°,∴△AED≌△CFB,
∴AE=CF.
又∵ ∠AEF=∠CFE=90°,
∴ AE∥CF,
∴四边形AFCE是平行四边形.
例2 如图,已知E,F是四边形ABCD对角线上两点,且AF=CE,DF=BE,DF∥BE,试说明四边形ABCD为平行四边形.
解:由AF=CE,得AE=CF.
又∵DF∥BE,
∴∠DFA=∠BEC,
∴∠DFC=∠BEA.
又∵DF=BE,
∴△CDF≌△ABE(SAS),
∴CD=AB,∠DCA=∠CAB,
例题与练习
∴CD∥AB,
∴四边形ABCD为平行四边形.
例3 如图,在四边形ABCD中,对角线AC与BD相交于点O,在①AB∥CD;②AO=CO;③AD=BC中任意选取两个作为条件,“四边形ABCD是平行四边形”作为结论构造命题.以①②作为条件构成的命题是真命题吗?若是,请证明;若不是,请举出反例.
解:以①②作为条件构成的命题是真命题.
证明如下:∵AB∥CD,
∴∠OAB=∠OCD.在△AOB和△COD中,
∴OB=OD.
∵OA=OC,
∴四边形ABCD是平行四边形.
∴△AOB≌△COD(ASA),
例题与练习
练习
1.在四边形中,有两条边相等,另外两边也相等,则这个四边形
( )
A.一定是平行四边形
B.一定不是平行四边形
C.可能是平行四边形,也可能不是平行四边形
D.上述答案都不对
C
2.如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6 cm,点P,Q分别从点A,C同时出发,点P以1 cm/s的速度由点A向点D运动,点Q以2 cm/s的速度由点C向点B运动,问几秒时,四边形ABQP是平行四边形?
解:设x s时,四边形ABQP是平行四边形.
根据题意,得AP=x,CQ=2x,
∴BQ=6-2x,
只有AP=BQ时,四边形ABQP才是平行四边形,
∴x=6-2x,解得x=2,
∴2 s时,四边形ABQP是平行四边形.
课堂小结
平行四边形的判定2
判定定理4
平行四边形的性质与判定的综合运用
一组对边平行且相等的四边形是平行四边形.
