人教版八年级数学下册 20.1.2 第2课时平均数、中位数和众数的应用 课件(共22张PPT)
文档属性
| 名称 | 人教版八年级数学下册 20.1.2 第2课时平均数、中位数和众数的应用 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 671.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 18:24:33 | ||
图片预览








文档简介
(共22张PPT)
第二十章 数据的分析
20.1 数据的集中趋势
第2课时 平均数、中位数和众数的应用
20.1.2 中位数和众数
导入新课
某公司员工的月工资如下:
经理说:“我公司员工收入很高,月平均工资为2000元.”
职员C说:“我的工资是1200元,在公司算中等收入.”
职员D说:“我们好几个人工资都是1100元.”
一位应聘者心里在琢磨,这个公司员工收入到底怎样呢?
探究新知
例1 某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元),数据如下:
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均的月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
思考
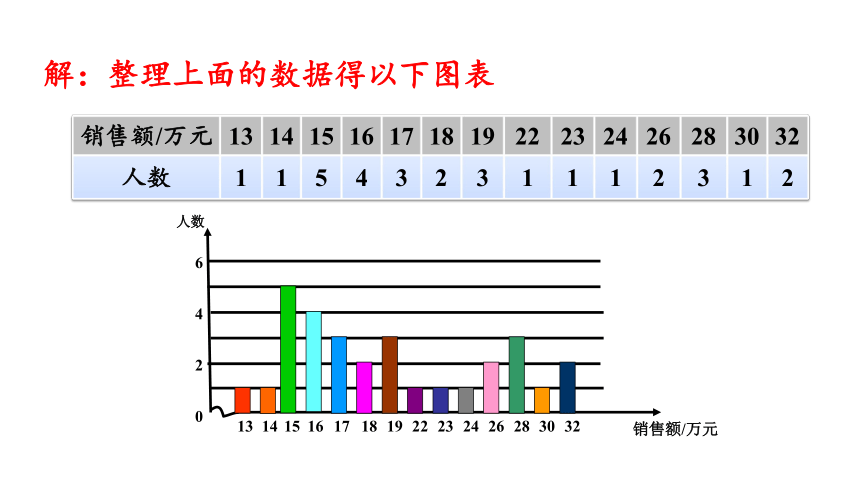
解:整理上面的数据得以下图表
0
4
2
6
人数
销售额/万元
13
14
15
16
17
18
19
22
23
24
26
28
30
32
探究新知
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均的月销售额是多少?
解:样本数据的众数是15,中位数是18,
利用计算器求得这组数据的平均数约是20.
可以推测,这个服装部营业员的月销售额为15万元的人数最多,中间的月销售额是18万元,平均月销售额大约是20万元.
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
解:这个目标可以定为每月20万元(平均数).因为从样本数据看,在平均数、中位数和众数中,平均数最大.可以估计,月销售额定为每月20万元是一个较高的目标,大约会有三分之一的营业员获得奖励.
思考
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
解:月销售额可以定为每月18万元(中位数).
思考
可以估计,如果月销售额定为18万元,将有一半左右的营业员获得奖励.
因为从样本情况看,月销售额在18万元以上(含18万元)的有16人,占总人数的一半左右.
知识归纳
平均数、中位数、众数的联系与区别
中位数仅与数据的排列位置有关,不受极端值或某些数据的变动;
平均数能充分利用各数据,在实际中较为常用,但受极端值影响,任何一个数据的变动都会引起平均数的变动;
众数主要研究各数据出现的次数,其大小只与这组数据中的某些数据有关.
联系:都反映了一组数据的集中趋势
例题与练习
例2 甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命是8年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下(单位:年):
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)分别写出以上三组数据的平均数、众数、中位数;
解:甲厂:8,5,6;
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
乙厂:9.6,8,8.5;
丙厂:9.4,4,8;
(2)这三个厂家推销广告分别用了哪一种表示集中趋势的特征数?
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
解:甲厂选用平均数8;
乙厂选用众数8;
丙厂选用中位数8;
(3)如果你是顾客,宜选购哪家工厂的产品?为什么?
解:宜选购乙厂的产品;
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
因为乙厂产品、平均使用寿命最长且多数超过8年或达到8年寿命.
例3 某中学开展演讲比赛活动,八(1)、八(2)班根据初赛成绩各选5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.
例题与练习
(1)根据下图填写下表:
85
100
解:∵两班的平均数相同,八(1)班的中位数较高,
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
∴八(1)班的复赛成绩较好;
解:∵八(1)班、八(2)班前两名选手的平均分分别为92.5分、100分,
(3)如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强?
∴在每班参加复赛的选手中分别选出2人参加决赛,
∴八(2)班的实力更强.
1.下面是某校八年级(2)班两组女生的体重(单位:kg)
第一组:35、36、38、40、42、42、75
第二组:35、36、38、40、42、42、45
(1)分别求这两组数据的平均数、众数、中位数,并解释他们的实际含义
练习
解:平均数=
(35+36+38+40+42+42+75)
_______________________
7
=44
(女生体重的平均值)
众数=42(第一组女生体重居多的重量)
中位数=40(处于第一组女生体重中间值的重量)
(2)比较这两组数据的平均数、众数、中位数,谈谈你对他们的认识.
解:两组女生的体重都集中在40Kg左右,平均体重分别是44、40,中位数反映的是数据数量大小排列以后求得的“中点”,表示两组女生的体重有一半少于40Kg,一半大于40Kg,两组众数和中位数相等,第一组的平均数大于第二组的平均数,主要是受最大体重75Kg的影响.
练习
练习
2.抽样调查了某班30位女生所穿鞋子的尺码,数据如下(单位:码).在这组数据的平均数、中位数和众数中,鞋厂最感兴趣的是( )
A.平均数 B.中位数
C.众数 D.无法确定
C
3.小明最近6次测验的成绩依次为:90分,85分,70分,65分,85分,75分.
(1)这6次测验成绩的平均数、中位数和众数分别是多少?
(2)如果他希望告诉别人他的成绩不错,那么他会选用哪个数表示他的成绩?
练习
解:(1)平均数:
=(90+85+70+65+85+75)÷6 ≈78.3
x
_
中位数:(85+75)÷2=80
众数为85
(2)小明会选择众数来表示自己的成绩不错.
课堂小结
平均数、中位数和众数的应用
平均数、中位数、众数的实际应用
平均数、中位数、众数的特征
第二十章 数据的分析
20.1 数据的集中趋势
第2课时 平均数、中位数和众数的应用
20.1.2 中位数和众数
导入新课
某公司员工的月工资如下:
经理说:“我公司员工收入很高,月平均工资为2000元.”
职员C说:“我的工资是1200元,在公司算中等收入.”
职员D说:“我们好几个人工资都是1100元.”
一位应聘者心里在琢磨,这个公司员工收入到底怎样呢?
探究新知
例1 某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元),数据如下:
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均的月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
思考
解:整理上面的数据得以下图表
0
4
2
6
人数
销售额/万元
13
14
15
16
17
18
19
22
23
24
26
28
30
32
探究新知
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均的月销售额是多少?
解:样本数据的众数是15,中位数是18,
利用计算器求得这组数据的平均数约是20.
可以推测,这个服装部营业员的月销售额为15万元的人数最多,中间的月销售额是18万元,平均月销售额大约是20万元.
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
解:这个目标可以定为每月20万元(平均数).因为从样本数据看,在平均数、中位数和众数中,平均数最大.可以估计,月销售额定为每月20万元是一个较高的目标,大约会有三分之一的营业员获得奖励.
思考
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
解:月销售额可以定为每月18万元(中位数).
思考
可以估计,如果月销售额定为18万元,将有一半左右的营业员获得奖励.
因为从样本情况看,月销售额在18万元以上(含18万元)的有16人,占总人数的一半左右.
知识归纳
平均数、中位数、众数的联系与区别
中位数仅与数据的排列位置有关,不受极端值或某些数据的变动;
平均数能充分利用各数据,在实际中较为常用,但受极端值影响,任何一个数据的变动都会引起平均数的变动;
众数主要研究各数据出现的次数,其大小只与这组数据中的某些数据有关.
联系:都反映了一组数据的集中趋势
例题与练习
例2 甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命是8年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下(单位:年):
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)分别写出以上三组数据的平均数、众数、中位数;
解:甲厂:8,5,6;
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
乙厂:9.6,8,8.5;
丙厂:9.4,4,8;
(2)这三个厂家推销广告分别用了哪一种表示集中趋势的特征数?
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
解:甲厂选用平均数8;
乙厂选用众数8;
丙厂选用中位数8;
(3)如果你是顾客,宜选购哪家工厂的产品?为什么?
解:宜选购乙厂的产品;
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
因为乙厂产品、平均使用寿命最长且多数超过8年或达到8年寿命.
例3 某中学开展演讲比赛活动,八(1)、八(2)班根据初赛成绩各选5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.
例题与练习
(1)根据下图填写下表:
85
100
解:∵两班的平均数相同,八(1)班的中位数较高,
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
∴八(1)班的复赛成绩较好;
解:∵八(1)班、八(2)班前两名选手的平均分分别为92.5分、100分,
(3)如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强?
∴在每班参加复赛的选手中分别选出2人参加决赛,
∴八(2)班的实力更强.
1.下面是某校八年级(2)班两组女生的体重(单位:kg)
第一组:35、36、38、40、42、42、75
第二组:35、36、38、40、42、42、45
(1)分别求这两组数据的平均数、众数、中位数,并解释他们的实际含义
练习
解:平均数=
(35+36+38+40+42+42+75)
_______________________
7
=44
(女生体重的平均值)
众数=42(第一组女生体重居多的重量)
中位数=40(处于第一组女生体重中间值的重量)
(2)比较这两组数据的平均数、众数、中位数,谈谈你对他们的认识.
解:两组女生的体重都集中在40Kg左右,平均体重分别是44、40,中位数反映的是数据数量大小排列以后求得的“中点”,表示两组女生的体重有一半少于40Kg,一半大于40Kg,两组众数和中位数相等,第一组的平均数大于第二组的平均数,主要是受最大体重75Kg的影响.
练习
练习
2.抽样调查了某班30位女生所穿鞋子的尺码,数据如下(单位:码).在这组数据的平均数、中位数和众数中,鞋厂最感兴趣的是( )
A.平均数 B.中位数
C.众数 D.无法确定
C
3.小明最近6次测验的成绩依次为:90分,85分,70分,65分,85分,75分.
(1)这6次测验成绩的平均数、中位数和众数分别是多少?
(2)如果他希望告诉别人他的成绩不错,那么他会选用哪个数表示他的成绩?
练习
解:(1)平均数:
=(90+85+70+65+85+75)÷6 ≈78.3
x
_
中位数:(85+75)÷2=80
众数为85
(2)小明会选择众数来表示自己的成绩不错.
课堂小结
平均数、中位数和众数的应用
平均数、中位数、众数的实际应用
平均数、中位数、众数的特征
