河南省周口阳金一中2012-2013学年高二学业水平模拟考试数学试题
文档属性
| 名称 | 河南省周口阳金一中2012-2013学年高二学业水平模拟考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 113.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-25 20:05:46 | ||
图片预览



文档简介
河南省周口阳金一中2012-2013学年高二学业水平模拟考试数学
1.考试采用书面答卷闭卷方式,考试时间90分钟,满分100分;
2.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
参考公式:柱体体积公式 ,锥体体积公式 (其中为底面面积,为高);
球的表面积公式 (其中为球的半径).
第Ⅰ卷
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1) 下列说法正确的是( )
A. B. C. D.
(2)直线的斜率是3,且过点A(1,-2),则直线的方程是( )
A. B.
C. D.
(3)不等式的解集为 ( )
A. B.
C. D.
(4)已知平面向量,,且,
则的值为( )
A.-3 B.-1 C.1 D. 3
(5)按右图所示的程序框图运算,若输入,则
输出的值是( )
A.3 B.4 C.5 D.6
(6)若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )
A. B. C. D.
(7)已知角的终边上一点的坐标为(,),则角的最小正值为( )
A. B. C. D.
(8)的内角的对边分别为,若,,则等于( )A. B.2 C. D.
(9)设用二分法求方程在区间(1,2)上近似解的过程中,计算得到,则方程的根落在区间( )A.(1,1.25) B. (1.25,1.5) C.(1.5, 1.75) D. (1.75,2)
(10)一个与球心距离为1的平面截球所得的圆面积为,则球的表面积为( )
A. B. C. D.
(11)完成一项装修工程,木工和瓦工的比例为2∶3,请木工需付日工资每人50元,请瓦工需付日工资每人40元,现有日工资预算2 000元,设每天请木工x人、瓦工y人,则每天请木、瓦工人数的约束条件是( )
A. B.
C. D.
(12)从中随机选取一个数为,从中随机选取一个数为,则的概率是( )A. B. C. D.
第Ⅱ卷
二、填空题:本大题共4小题,每小题3分,共12分.
(13) 若集合,,且,则实数取值的集合
为 .
(14)某校有学生2000人,其中高三学生500人,为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校学生中抽取一个200人的样本,则样本中高三学生的人数为 .
(15)设函数,则的最大值为_ _ .
(16)在集合上定义两种运算和(如下图),则______.
三、解答题:本大题共5小题,共52分.解答应写出文字说明、证明过程或演算步骤.
(17)(本小题满分10分)
已知一条曲线上的点到定点的距离是到定点距离的二倍,求这条曲线的方程.
(18)(本小题满分10分)
一种放射性元素,最初的质量为500g,按每年10﹪衰减.(Ⅰ)求t年后,这种放射性元素质量ω的表达式;
(Ⅱ)由求出的函数表达式,求这种放射性元素的半衰期(剩留量为原来的一半所需要的时间).(精确到0.1;参考数据:)
(19)(本小题满分10分)
记等差数列{}的前n项和为,已知,.
(Ⅰ)求数列{}的通项公式;
(Ⅱ)令,求数列{}的前项和.
(20)(本小题满分10分)
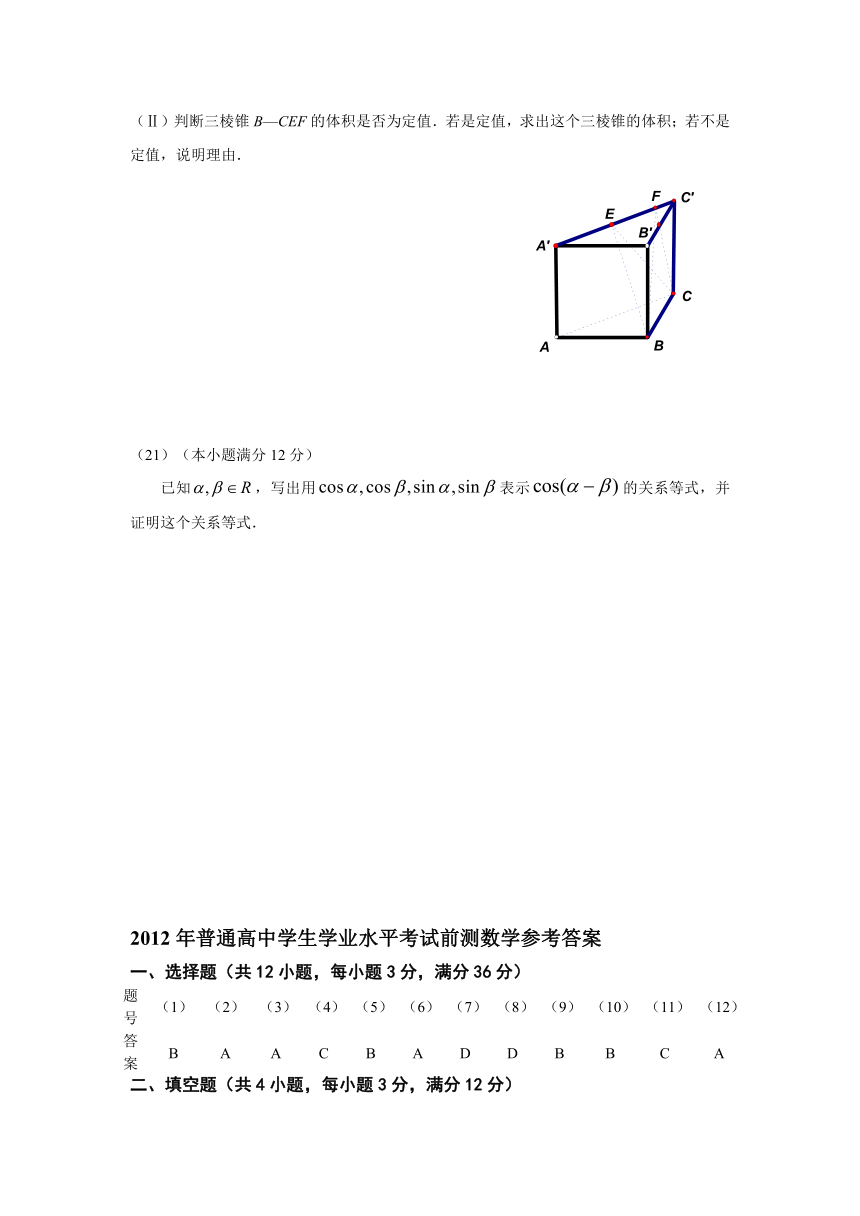
如图,在直三棱柱中,,.棱上有两个动点E,F,且EF = a (a为常数).
(Ⅰ)在平面ABC内确定一条直线,使该直线与直线CE垂直;
(Ⅱ)判断三棱锥B—CEF的体积是否为定值.若是定值,求出这个三棱锥的体积;若不是定值,说明理由.
(21)(本小题满分12分)
已知,写出用表示的关系等式,并证明这个关系等式.
2012年普通高中学生学业水平考试前测数学参考答案
一、选择题(共12小题,每小题3分,满分36分)
题号
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
答案
B
A
A
C
B
A
D
D
B
B
C
A
二、填空题(共4小题,每小题3分,满分12分)
(13){﹣1,0,1} (14)50 (15)8 (16)
三、解答题(共5小题,满分52分)
(17)解:设M(x,y)是曲线上任意的一点,点M在曲线上的条件是
. -------4分
由两点间距离公式,上式用坐标表示为
,
两边平方并化简得所求曲线方程
------10分
(18)解:(Ⅰ)最初的质量为500g,
经过1年,ω=500(1-10﹪)=500×,
经过2年,ω=500×,
……,
由此推出,t年后,ω=500×. ------5分
(Ⅱ)解方程500×=250.
=,
,
,
所以,这种放射性元素的半衰期约为年. ------10分
(19)解:(Ⅰ)设等差数列{}的公差为d,由已知条件得
可得数列{}的通项公式为=n. ------4分
(Ⅱ)
=-
=
= ------10分
(20)解: (Ⅰ)取AC中点D,连接BD.
,D为底边AC中点,∴.
∵.
又,∴直线.
∵
∴. ------5分
(Ⅱ)直线,
.
EF上的高为线段,
由已知条件得,
故
由(Ⅰ)可知,.
在等腰三角形ABC中,可求得BD=,
.------10分
(21)解: ------2分
证明:如图,在平面直角坐标系
xoy内作单位圆O,以Ox为始边作角
,它们的终边与单位圆的交点分别
为A,B.
则 ,
.
由向量数量积的定义,有
.
由向量数量积的的坐标表示,有
于是
. ①------7分
对于任意的,总可选取适当的整数k,使得=+或
=-+成立.
故对于任意的,总有成立,带入①式得
对,总有
成立.------12分
另证:由于都是任意角,也是任意角.由诱导公式,总可以找到一个角.
当 时,,则有
,带入①既得
.
当时,,就是的夹角,则有
,带入①既得
.
综上,对,总有
.------12分
注:1、解答题其他解、证方法可参照以上参考答案酌情给分;
2、解答题各题解、证过程的给分点,可酌情细化.
1.考试采用书面答卷闭卷方式,考试时间90分钟,满分100分;
2.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
参考公式:柱体体积公式 ,锥体体积公式 (其中为底面面积,为高);
球的表面积公式 (其中为球的半径).
第Ⅰ卷
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1) 下列说法正确的是( )
A. B. C. D.
(2)直线的斜率是3,且过点A(1,-2),则直线的方程是( )
A. B.
C. D.
(3)不等式的解集为 ( )
A. B.
C. D.
(4)已知平面向量,,且,
则的值为( )
A.-3 B.-1 C.1 D. 3
(5)按右图所示的程序框图运算,若输入,则
输出的值是( )
A.3 B.4 C.5 D.6
(6)若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )
A. B. C. D.
(7)已知角的终边上一点的坐标为(,),则角的最小正值为( )
A. B. C. D.
(8)的内角的对边分别为,若,,则等于( )A. B.2 C. D.
(9)设用二分法求方程在区间(1,2)上近似解的过程中,计算得到,则方程的根落在区间( )A.(1,1.25) B. (1.25,1.5) C.(1.5, 1.75) D. (1.75,2)
(10)一个与球心距离为1的平面截球所得的圆面积为,则球的表面积为( )
A. B. C. D.
(11)完成一项装修工程,木工和瓦工的比例为2∶3,请木工需付日工资每人50元,请瓦工需付日工资每人40元,现有日工资预算2 000元,设每天请木工x人、瓦工y人,则每天请木、瓦工人数的约束条件是( )
A. B.
C. D.
(12)从中随机选取一个数为,从中随机选取一个数为,则的概率是( )A. B. C. D.
第Ⅱ卷
二、填空题:本大题共4小题,每小题3分,共12分.
(13) 若集合,,且,则实数取值的集合
为 .
(14)某校有学生2000人,其中高三学生500人,为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校学生中抽取一个200人的样本,则样本中高三学生的人数为 .
(15)设函数,则的最大值为_ _ .
(16)在集合上定义两种运算和(如下图),则______.
三、解答题:本大题共5小题,共52分.解答应写出文字说明、证明过程或演算步骤.
(17)(本小题满分10分)
已知一条曲线上的点到定点的距离是到定点距离的二倍,求这条曲线的方程.
(18)(本小题满分10分)
一种放射性元素,最初的质量为500g,按每年10﹪衰减.(Ⅰ)求t年后,这种放射性元素质量ω的表达式;
(Ⅱ)由求出的函数表达式,求这种放射性元素的半衰期(剩留量为原来的一半所需要的时间).(精确到0.1;参考数据:)
(19)(本小题满分10分)
记等差数列{}的前n项和为,已知,.
(Ⅰ)求数列{}的通项公式;
(Ⅱ)令,求数列{}的前项和.
(20)(本小题满分10分)
如图,在直三棱柱中,,.棱上有两个动点E,F,且EF = a (a为常数).
(Ⅰ)在平面ABC内确定一条直线,使该直线与直线CE垂直;
(Ⅱ)判断三棱锥B—CEF的体积是否为定值.若是定值,求出这个三棱锥的体积;若不是定值,说明理由.
(21)(本小题满分12分)
已知,写出用表示的关系等式,并证明这个关系等式.
2012年普通高中学生学业水平考试前测数学参考答案
一、选择题(共12小题,每小题3分,满分36分)
题号
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
答案
B
A
A
C
B
A
D
D
B
B
C
A
二、填空题(共4小题,每小题3分,满分12分)
(13){﹣1,0,1} (14)50 (15)8 (16)
三、解答题(共5小题,满分52分)
(17)解:设M(x,y)是曲线上任意的一点,点M在曲线上的条件是
. -------4分
由两点间距离公式,上式用坐标表示为
,
两边平方并化简得所求曲线方程
------10分
(18)解:(Ⅰ)最初的质量为500g,
经过1年,ω=500(1-10﹪)=500×,
经过2年,ω=500×,
……,
由此推出,t年后,ω=500×. ------5分
(Ⅱ)解方程500×=250.
=,
,
,
所以,这种放射性元素的半衰期约为年. ------10分
(19)解:(Ⅰ)设等差数列{}的公差为d,由已知条件得
可得数列{}的通项公式为=n. ------4分
(Ⅱ)
=-
=
= ------10分
(20)解: (Ⅰ)取AC中点D,连接BD.
,D为底边AC中点,∴.
∵.
又,∴直线.
∵
∴. ------5分
(Ⅱ)直线,
.
EF上的高为线段,
由已知条件得,
故
由(Ⅰ)可知,.
在等腰三角形ABC中,可求得BD=,
.------10分
(21)解: ------2分
证明:如图,在平面直角坐标系
xoy内作单位圆O,以Ox为始边作角
,它们的终边与单位圆的交点分别
为A,B.
则 ,
.
由向量数量积的定义,有
.
由向量数量积的的坐标表示,有
于是
. ①------7分
对于任意的,总可选取适当的整数k,使得=+或
=-+成立.
故对于任意的,总有成立,带入①式得
对,总有
成立.------12分
另证:由于都是任意角,也是任意角.由诱导公式,总可以找到一个角.
当 时,,则有
,带入①既得
.
当时,,就是的夹角,则有
,带入①既得
.
综上,对,总有
.------12分
注:1、解答题其他解、证方法可参照以上参考答案酌情给分;
2、解答题各题解、证过程的给分点,可酌情细化.
同课章节目录
