华师大版数学八下17.2.2函数的图像 课件(22张ppt)
文档属性
| 名称 | 华师大版数学八下17.2.2函数的图像 课件(22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 18:37:15 | ||
图片预览





文档简介
(共22张PPT)
华东师大版·八年级数学下册
2 函数的图象
17.2函数的图像
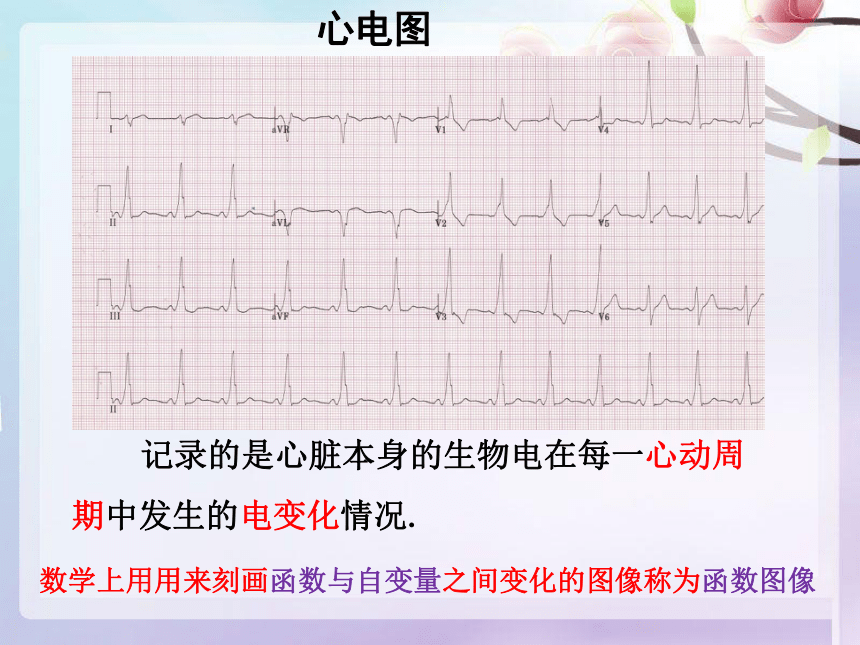
心电图
记录的是心脏本身的生物电在每一心动周期中发生的电变化情况.
数学上用用来刻画函数与自变量之间变化的图像称为函数图像
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
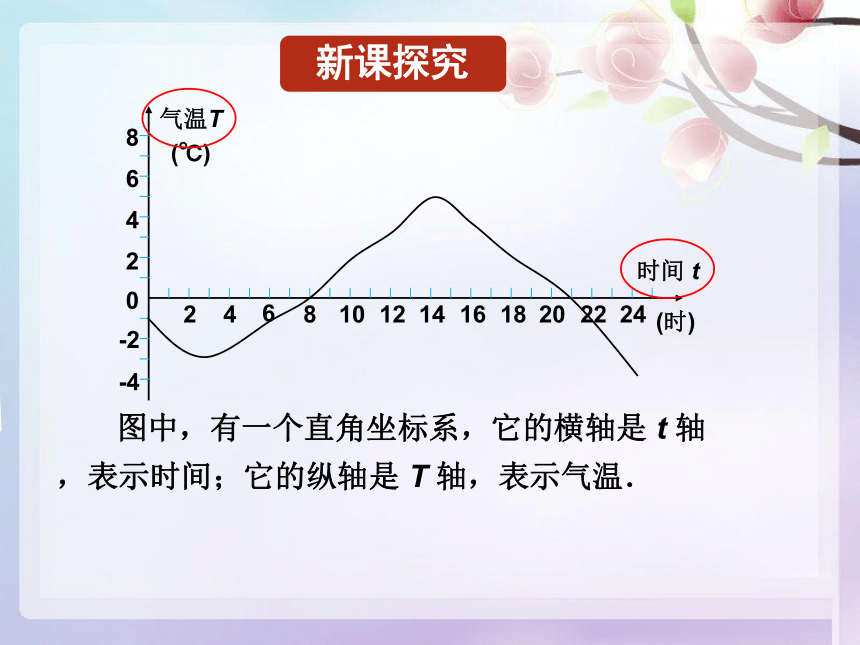
某地一天内的气温变化图.
说一说,你是如何在图中找到各个时刻的气温的?
回顾
新课探究
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
图中,有一个直角坐标系,它的横轴是 t 轴,表示时间;它的纵轴是 T 轴,表示气温.
这一气温曲线实际上给出了某日的气温 T(℃)与时间 t(时)的函数关系.
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
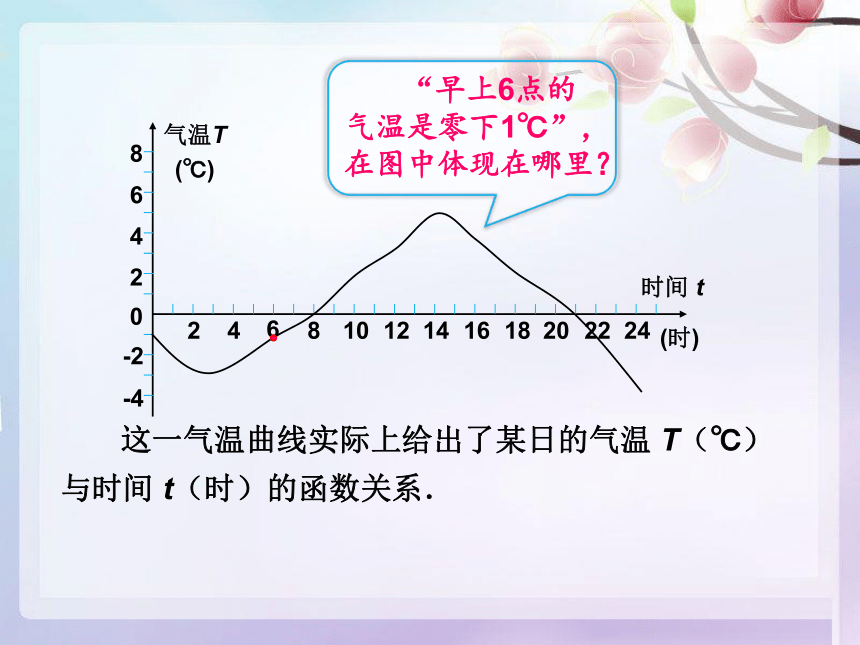
“早上6点的气温是零下1℃”,在图中体现在哪里?
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
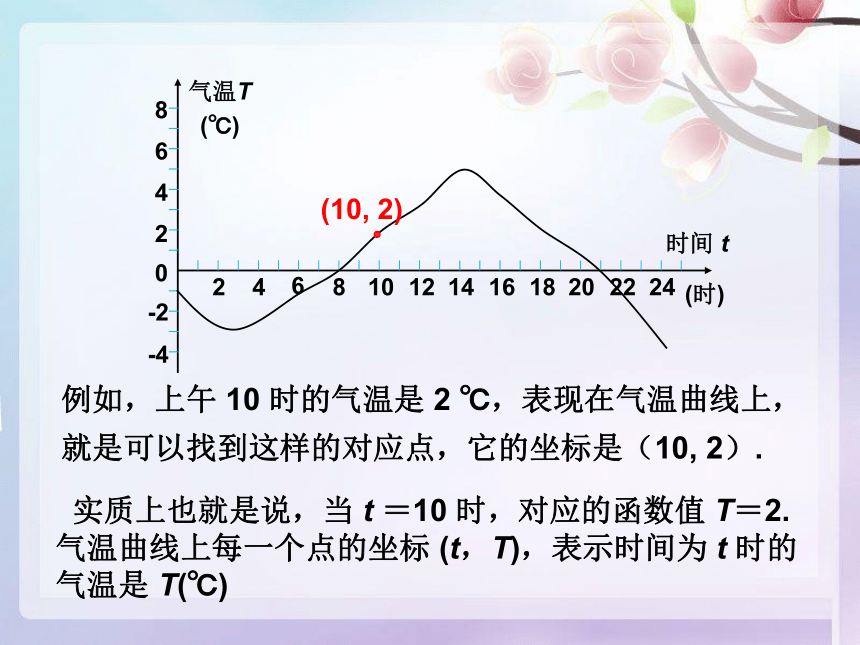
例如,上午 10 时的气温是 2 ℃,表现在气温曲线上,就是可以找到这样的对应点,它的坐标是(10, 2).
(10, 2)
实质上也就是说,当 t =10 时,对应的函数值 T=2. 气温曲线上每一个点的坐标 (t,T),表示时间为 t 时的气温是 T(℃)
从图中我们可以看出,随着时间 t(时)的变化,相应的气温 T(℃)也随之变化.
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
温度升高
温度降低
气温曲线是用图象表示函数的一个实际例子.那么,什么是函数的图象呢?
思考
一般来说, 函数的图象是由直角坐标系中的一系列点组成.
概括
图象上每一点的坐标 (x, y) 代表了函数的一对对应值,它的横坐标 x 表示自变量的某一取值,纵坐标 y 表示与它对应的函数值.
-3
-2
-1
O
1
2
3
x
1
2
3
-1
-2
y
-3
y = x
例1 画出函数 的图象.
分析:函数图象上的点一般来说有无数多个,要把每个点都作出来得到函数图象很困难,甚至是不可能的.所以我们常作出函数图象上的一部分点,然后用光滑的曲线把这些点连接起来得到函数的图象.
请同学们想一想,怎么才能得到图象上的一部分点呢
为此,我们首先要取一些自变量x的值,求出对应的
函数值y,那么以(x,y)为坐标的点就是函数图象上的点.为了表达方便,我们可以列表来表示x和y的对应关系.
解:取自变量的一些值,例如-3、-2、-1、0、1、2、3,
计算出对应的函数值,列表表示:
例1 画出函数 的图象.
4.5
2
0.5
0
0.5
2
4.5
x … -3 -2 -1 0 1 2 3 …
y …
…
x
o
-4
-3
-2
-1
1
2
3
4
5
-5
y
1
2
3
4
5
大家自己总结一下,看看我们在做这个函数图象的时候都经过了哪些步骤
(-3,4.5)
第一步,列表——表中给出一些自变量的值(注意自变量的取值范围)及其 ;
第二步,描点——在平面直角坐标系中,以自
变量的值为 ,相应的函数值为 ,描出表格中各数对对应的各点;
第三步:连线——按照横坐标 的顺序,
把所描出的各点用 连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
归纳总结
画函数图象的一般步骤:
1、在所给的直角坐标系中画出函数 的图象
x -3 -2 -1 0 1 2 3
y
-1.5
-1
-0.5
0
0.5
1
1.5
教材38页练习1
(1)试判断点A(-1,3)和点B 是否在此函数的图象上;
(2)已知点C(a,a+1)在此函数的图象上,求a的值.
x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6
y
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
2、画出函数 的图象
注意:取自变量所的值
应在其取值范围内
教材38页练习2
为什么没有“0”?
(教材39页)例2、 王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷 先上,然后追赶爷爷.中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时),看图回答下列问题:
(1)小强让爷爷先上多少米?
(2)山顶高多少米?谁先爬上山顶?
(3)小强通过多少时间追少爷爷?
(4) 谁的速度大,大多少?
解:由图象可知:
(1)小强出发0分钟时,爷爷已经爬山60米,因此小强让爷爷先上60米;
(2)山顶离山脚的距离是300米,小强先爬上山;
(3)因为小强和爷爷路程相等时是8分钟,所以小强用了8分钟追上爷爷;
(4)小强爬山300米用了10分钟,速度为30米/分,爷爷爬山(300-60)米=240米,用了10.5分钟,速度约为23米/分,因此小强的速度大,大7米/分.
1.下图为世界总人口数的变化图.根据该图回答:
(1)从1830年到1998年,世界总人口数呈怎样的变化趋势?
(2)在图中,显示哪一段时间中世界总人口数变化最快?
解:
(1)世界总人口数呈逐年增长的趋势,尤其自1960年开始,增长率明显加快。
(2)从1830年到1930年的100年间,世界总人口只增长10亿,1930年到1960年的30年间,世界总人口增长10亿,1960年到1976年的16年间,增长10亿,1976年到1987年的11年间,增长10亿,1987年到1998年间,增长9亿多,因此,1976年至1987年这段时间中世界总人口数变化最快。
2.一枝蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则下列3幅图象中能大致刻画出这枝蜡烛点燃后剩下的长度h(厘米)与点燃时间t之间的函数关系的是( ).
C
3.小明从家里出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家.下面的图描述了小明在散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.请你由图具体说明小明散步的情况.
小明先走了约3分钟,到达离家250米处的一个阅报栏前看了5分钟报,又向前走了2分钟,到达离家450米处返回,走了6分钟到家。
解:
4.某装水的水池按一定的速度放掉水池的一半后,停止放水并立即按一定的速度注水,水池注满后,停止注水,又立即按一定的速度放完水池的水。若水池的存水量为v(立方米),放水或注水的时间为t(分钟),则v与t的关系的大致图象只能是( )
A
锥形瓶
由函数解析式画函数图象,一般按下列步骤进行:
1.列表:列表给出自变量与函数的一些对应值;
2.描点:以表中对应值为坐标,在坐标平面内描出相
应的点;
3.连线:按照自变量由小到大的顺序,把所描各点用
光滑的曲线连结起来.
华东师大版·八年级数学下册
2 函数的图象
17.2函数的图像
心电图
记录的是心脏本身的生物电在每一心动周期中发生的电变化情况.
数学上用用来刻画函数与自变量之间变化的图像称为函数图像
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
某地一天内的气温变化图.
说一说,你是如何在图中找到各个时刻的气温的?
回顾
新课探究
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
图中,有一个直角坐标系,它的横轴是 t 轴,表示时间;它的纵轴是 T 轴,表示气温.
这一气温曲线实际上给出了某日的气温 T(℃)与时间 t(时)的函数关系.
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
“早上6点的气温是零下1℃”,在图中体现在哪里?
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
例如,上午 10 时的气温是 2 ℃,表现在气温曲线上,就是可以找到这样的对应点,它的坐标是(10, 2).
(10, 2)
实质上也就是说,当 t =10 时,对应的函数值 T=2. 气温曲线上每一个点的坐标 (t,T),表示时间为 t 时的气温是 T(℃)
从图中我们可以看出,随着时间 t(时)的变化,相应的气温 T(℃)也随之变化.
0
2
4
6
8
-2
-4
2
4
6
8
10
12
14
16
18
20
22
24
气温T
(℃)
时间 t
(时)
温度升高
温度降低
气温曲线是用图象表示函数的一个实际例子.那么,什么是函数的图象呢?
思考
一般来说, 函数的图象是由直角坐标系中的一系列点组成.
概括
图象上每一点的坐标 (x, y) 代表了函数的一对对应值,它的横坐标 x 表示自变量的某一取值,纵坐标 y 表示与它对应的函数值.
-3
-2
-1
O
1
2
3
x
1
2
3
-1
-2
y
-3
y = x
例1 画出函数 的图象.
分析:函数图象上的点一般来说有无数多个,要把每个点都作出来得到函数图象很困难,甚至是不可能的.所以我们常作出函数图象上的一部分点,然后用光滑的曲线把这些点连接起来得到函数的图象.
请同学们想一想,怎么才能得到图象上的一部分点呢
为此,我们首先要取一些自变量x的值,求出对应的
函数值y,那么以(x,y)为坐标的点就是函数图象上的点.为了表达方便,我们可以列表来表示x和y的对应关系.
解:取自变量的一些值,例如-3、-2、-1、0、1、2、3,
计算出对应的函数值,列表表示:
例1 画出函数 的图象.
4.5
2
0.5
0
0.5
2
4.5
x … -3 -2 -1 0 1 2 3 …
y …
…
x
o
-4
-3
-2
-1
1
2
3
4
5
-5
y
1
2
3
4
5
大家自己总结一下,看看我们在做这个函数图象的时候都经过了哪些步骤
(-3,4.5)
第一步,列表——表中给出一些自变量的值(注意自变量的取值范围)及其 ;
第二步,描点——在平面直角坐标系中,以自
变量的值为 ,相应的函数值为 ,描出表格中各数对对应的各点;
第三步:连线——按照横坐标 的顺序,
把所描出的各点用 连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
归纳总结
画函数图象的一般步骤:
1、在所给的直角坐标系中画出函数 的图象
x -3 -2 -1 0 1 2 3
y
-1.5
-1
-0.5
0
0.5
1
1.5
教材38页练习1
(1)试判断点A(-1,3)和点B 是否在此函数的图象上;
(2)已知点C(a,a+1)在此函数的图象上,求a的值.
x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6
y
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
2、画出函数 的图象
注意:取自变量所的值
应在其取值范围内
教材38页练习2
为什么没有“0”?
(教材39页)例2、 王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷 先上,然后追赶爷爷.中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时),看图回答下列问题:
(1)小强让爷爷先上多少米?
(2)山顶高多少米?谁先爬上山顶?
(3)小强通过多少时间追少爷爷?
(4) 谁的速度大,大多少?
解:由图象可知:
(1)小强出发0分钟时,爷爷已经爬山60米,因此小强让爷爷先上60米;
(2)山顶离山脚的距离是300米,小强先爬上山;
(3)因为小强和爷爷路程相等时是8分钟,所以小强用了8分钟追上爷爷;
(4)小强爬山300米用了10分钟,速度为30米/分,爷爷爬山(300-60)米=240米,用了10.5分钟,速度约为23米/分,因此小强的速度大,大7米/分.
1.下图为世界总人口数的变化图.根据该图回答:
(1)从1830年到1998年,世界总人口数呈怎样的变化趋势?
(2)在图中,显示哪一段时间中世界总人口数变化最快?
解:
(1)世界总人口数呈逐年增长的趋势,尤其自1960年开始,增长率明显加快。
(2)从1830年到1930年的100年间,世界总人口只增长10亿,1930年到1960年的30年间,世界总人口增长10亿,1960年到1976年的16年间,增长10亿,1976年到1987年的11年间,增长10亿,1987年到1998年间,增长9亿多,因此,1976年至1987年这段时间中世界总人口数变化最快。
2.一枝蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则下列3幅图象中能大致刻画出这枝蜡烛点燃后剩下的长度h(厘米)与点燃时间t之间的函数关系的是( ).
C
3.小明从家里出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家.下面的图描述了小明在散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.请你由图具体说明小明散步的情况.
小明先走了约3分钟,到达离家250米处的一个阅报栏前看了5分钟报,又向前走了2分钟,到达离家450米处返回,走了6分钟到家。
解:
4.某装水的水池按一定的速度放掉水池的一半后,停止放水并立即按一定的速度注水,水池注满后,停止注水,又立即按一定的速度放完水池的水。若水池的存水量为v(立方米),放水或注水的时间为t(分钟),则v与t的关系的大致图象只能是( )
A
锥形瓶
由函数解析式画函数图象,一般按下列步骤进行:
1.列表:列表给出自变量与函数的一些对应值;
2.描点:以表中对应值为坐标,在坐标平面内描出相
应的点;
3.连线:按照自变量由小到大的顺序,把所描各点用
光滑的曲线连结起来.
