1.2洛伦兹力同步训练(Word版含答案)
文档属性
| 名称 | 1.2洛伦兹力同步训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 596.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-11 09:10:17 | ||
图片预览




文档简介
1.2洛伦兹力
一、选择题(共15题)
1.如图所示,磁感应强度的方向、正电荷运动的方向、洛伦兹力的方向,三者之间关系正确的是( )
A. B. C. D.
2.如下图所示,磁场方向、电荷的运动方向、电荷所受洛伦兹力的方向两两垂直,则正确的是( )
A.B. C. D.
3.在垂直纸面向外的匀强磁场B中,有不计重力的a、b两个带电粒子,在纸面内做匀速圆周运动,运动方向和轨迹示意如图所示。下列说法正确的是( )
A.a、b两粒子所带电性相同
B.a粒子所带的电荷量较大
C.a粒子运动的速率较大
D.a粒子所做圆周运动的周期较长
4.一个带电粒子,沿垂直于磁场方向,射入匀强磁场中,粒子的一段径迹如图所示,径迹上的每一小段都可以近似看成圆弧.由于带电粒子使周围的空气电离,粒子的能量逐渐减小而带电量不变.不计粒子重力,从图中情况可以确定( )
A.粒子是带正电的,它所受的洛仑兹力大小不变
B.粒子是带正电的,它是由a点运动到b点
C.粒子是带负电的,它所受的洛仑兹力大小逐渐增大
D.粒子是带负电的,它是由a点运动到b点
5.一个质量为m、电量为q的粒子,以与匀强磁场B垂直的速度v射入磁场中,仅受洛仑兹力作用,则穿过粒子运动轨迹内的磁通量Φ与磁感应强度B大小的关系是( )
A.Φ∝B B.Φ∝ C.Φ∝B2 D.Φ∝
6.关于带电粒子在匀强磁场中的运动,下列说法正确的是( )
A.带电粒子飞入匀强磁场后,一定做匀速圆周运动
B.带电粒子飞入匀强磁场后做匀速圆周运动时,速度一定不变
C.带电粒子飞入匀强磁场后做匀速圆周运动时,洛伦兹力的方向总和运动方向垂直
D.带电粒子飞入匀强磁场后做匀速圆周运动时,加速度一定保持不变
7.有关电荷所受电场力和洛仑兹力的说法中,正确的是( )
A.电荷在电场中一定受电场力的作用
B.电荷在磁场中一定受磁场力的作用
C.电荷受电场力的方向与该处的电场方向一致
D.电荷若受磁场力,则受力方向与该处的磁场方向不一定垂直
8.关于电荷所受电场力和洛伦兹力,正确的说法是( )
A.电荷运动方向与电场方向平行时,不受电场力作用
B.电荷所受电场力方向一定与该处电场方向相同
C.电荷在磁场中一定受洛伦兹力作用
D.电荷所受的洛伦兹力方向一定与磁场方向垂直
9.电场和磁场的性质既有相似性,又各有其特殊性,下列关于电场和磁场有关性质的比较,正确的是( )
A.电荷在电场中必受电场力,运动电荷在磁场中必受洛伦兹力
B.电场线分布的疏密表示电场的强弱,磁感线分布的疏密表示磁场的强弱
C.电场方向与正电荷受电场力方向相同,磁场方向与正电荷受洛伦兹力方向相同
D.电场线和磁感线都是不闭合的
10.如图所示,当磁铁的磁极靠近阴极射线管时,荧光屏上的亮线发生了弯曲.这个现象说明
A.阴极射线中的粒子带负电
B.阴极射线中的粒子带正电
C.运动电荷的周围存在电场
D.运动电荷受到磁场的作用力
11.如图所示,磁场中固定一个电荷量为Q的正点电荷,一个电荷量为q,质量为m的带电粒子(重力不计)以正点电荷为圆心,在匀强磁场中做匀速圆周运动,测得以不同的绕行方向绕正电荷做半径为r的圆周运动时,周期之比为2:1,已知静电力常量为k,下列说法中正确的是( )
A.粒子可能带正电,以不同的绕行方向做圆周运动时,所受洛伦兹力大小相等
B.粒子一定带负电,且沿逆时针方向旋转时的线速度是沿顺时针方向时的
C.粒子顺时针旋转时,向心加速度大小为
D.粒子逆时针旋转时,向心加速度大小为
12.磁场中某区域的磁感线如图所示,下列说法中正确的是( )
A.a、b两处的磁感应强度大小
B.a、b两处的磁感应强度大小
C.一通电直导线分别放在a、b两处,所受的安培力大小一定有FaD.一电荷分别静止在a、b两处均受洛伦兹力,且大小一定有fa13.运动电荷进入匀强磁场后(无其他场),可能做( )
A.匀速圆周运动 B.匀速直线运动
C.匀加速直线运动 D.平抛运动
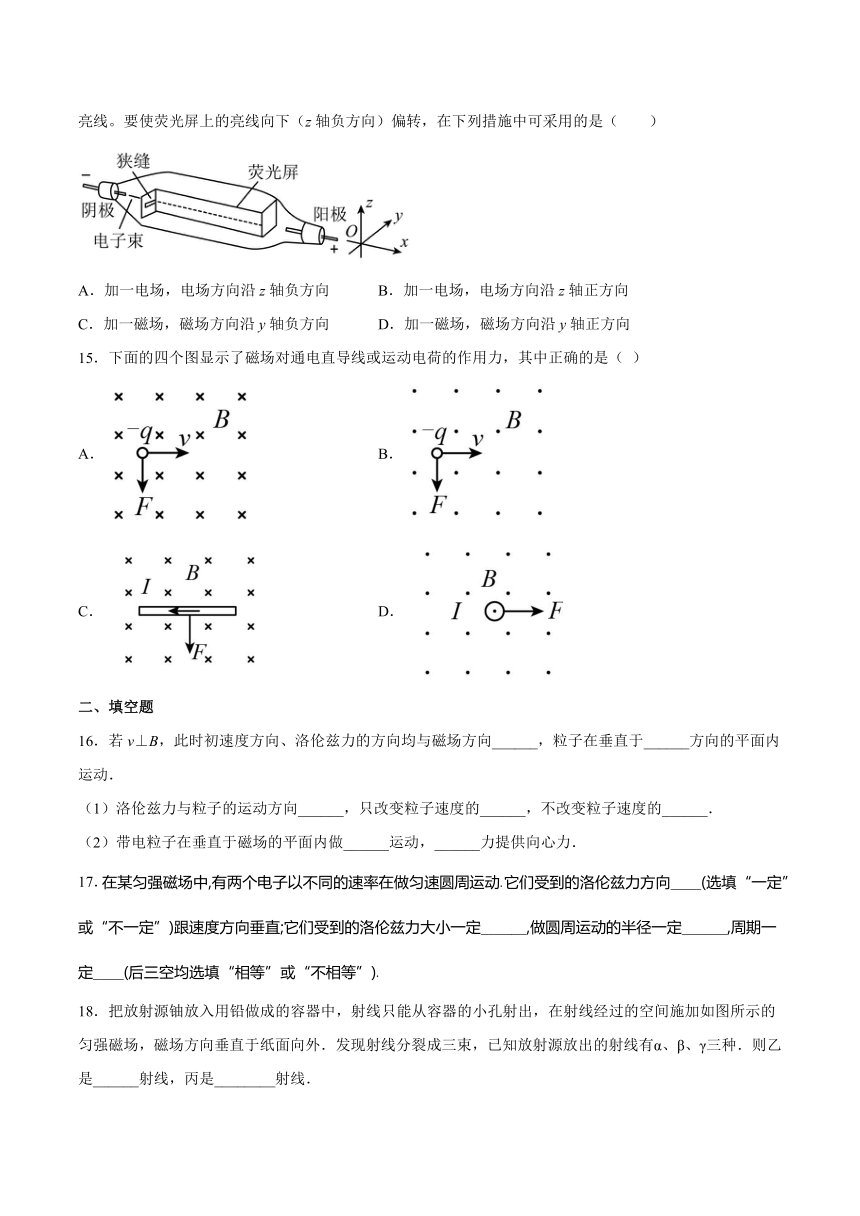
14.阴极射线管示意图如图所示。接通电源后,电子流由阴极沿x轴正方向射出,在荧光屏上会看到一条亮线。要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )
A.加一电场,电场方向沿z轴负方向 B.加一电场,电场方向沿z轴正方向
C.加一磁场,磁场方向沿y轴负方向 D.加一磁场,磁场方向沿y轴正方向
15.下面的四个图显示了磁场对通电直导线或运动电荷的作用力,其中正确的是( )
A. B.
C. D.
二、填空题
16.若v⊥B,此时初速度方向、洛伦兹力的方向均与磁场方向______,粒子在垂直于______方向的平面内运动.
(1)洛伦兹力与粒子的运动方向______,只改变粒子速度的______,不改变粒子速度的______.
(2)带电粒子在垂直于磁场的平面内做______运动,______力提供向心力.
17.在某匀强磁场中,有两个电子以不同的速率在做匀速圆周运动.它们受到的洛伦兹力方向____(选填“一定”或“不一定”)跟速度方向垂直;它们受到的洛伦兹力大小一定______,做圆周运动的半径一定______,周期一定____(后三空均选填“相等”或“不相等”).
18.把放射源铀放入用铅做成的容器中,射线只能从容器的小孔射出,在射线经过的空间施加如图所示的匀强磁场,磁场方向垂直于纸面向外.发现射线分裂成三束,已知放射源放出的射线有α、β、γ三种.则乙是______射线,丙是________射线.
19.一初速度为零的带电粒子,经电压为U的电场加速后进入磁感应强度为B的匀强磁场中,已知带电粒子的质量为m,电量为q,则带电粒子所受的洛仑兹力为______,轨道半径为______.
三、综合题
20.在宽L=10cm的区域内,存在着互相垂直的电场和磁场,如图所示.一束荷质比e/m=1.8×1011C/kg的电子以v =1.8×106m/s的速度垂直射入场中而恰好不改变运动方向.若去掉电场,电子穿过磁场区后偏离原方向5cm.那么如果去掉磁场而保持原电场,电子将偏离原方向多远?
21.在一个放射源水平放射出、 和三种射线,垂直射入如图所示磁场.区域Ⅰ和Ⅱ的宽度均为d,各自存在着垂直纸面的匀强磁场,两区域的磁感强度大小B相等,方向相反(粒子运动不考虑相对论效应).
(1)若要筛选出速率大于v1的粒子进入区域Ⅱ,要求磁场宽度d与B和v1的关系.
(2)若B=0.0034T,V1=0.1c(c是光速度),则可得d; 粒子的速率为0.001c,计算和射线离开区域Ⅰ时的距离;并给出去除和射线的方法.
(3)当d满足第(1)小题所给关系时,请给出速率在;区间的粒子离开区域Ⅱ时的位置和方向.
(4)请设计一种方案,能使离开区域Ⅱ的粒子束在右侧聚焦且水平出射.
已知:电子质量, 粒子质量,电子电荷量 ,(时)
22.如图所示,在水平面内固定一个半径为R的半圆形光滑细玻璃管,处于垂直纸面方向的匀强磁场中,磁感应强度大小为B。以管的一端O为坐标原点,以其直径为x轴建立平面直角坐标系。一个质量为m,带电量为+q的小球(小球可视为质点)从O端以一定的初速度入射,在玻璃管内运动时恰好不受玻璃管侧壁的作用力。
(1)判断所加磁场的方向,并求出小球入射的初速度大小;
(2)若撤掉磁场,在水平方向施加一个沿y轴负向的匀强电场,已知小球在玻璃管内运动过程中,动能最小值为入射动能的一半,请写出小球在管内运动的动能Ek随x变化的函数;
(3)在(2)问题的基础上,求小球受到玻璃管侧壁作用力的最小值。
23.如图所示,半径R=0.5m的金属圆筒a内同轴放置一半径稍小的金属圆筒b,筒a外部有平行于圆筒轴线、范围足够大的匀强磁场,磁感应强度B=0.2T.两圆筒之间加有U=150V的电压,使两圆筒间产生强电场.一比荷为q/m=104C/kg的带正电粒子从紧贴b筒的M点由静止释放,经电场加速后,穿过a筒上正对M点的小孔,垂直进入匀强磁场(不计粒子重力).
(1)求带电粒子在磁场中做圆周运动的轨道半径r
(2)若粒子从小孔射出的同时,圆筒a、b以相同的角速度沿逆时针方向绕轴线高速旋转.为使粒子在不碰到圆筒a的情况下,还能返回到出发点M,则圆筒旋转的角速度ω应满足什么条件?(忽略筒旋转引起的磁场变化,不计粒子在两筒间运动的时间)
试卷第1页,共3页
参考答案:
1.C
【详解】
根据左手定则可知;
A.该图中洛伦兹力方向向左,选项A错误;
B.该图中洛伦兹力方向向右,选项B错误;
C.该图中洛伦兹力方向向下,选项C正确;
D.该图中洛伦兹力方向向左,选项D错误;
故选C。
2.D
【详解】
A.根据左手定则,该图中洛伦兹力的方向竖直向下,选项A错误;
B.根据左手定则,该图中洛伦兹力的方向水平向右,选项B错误;
C.根据左手定则,该图中洛伦兹力的方向水平向右,选项C错误;
D.根据左手定则,该图中洛伦兹力的方向垂直纸面向外,选项D正确。
故选D。
3.A
【详解】
A.两粒子均逆时针运动,磁场垂直纸面向外,根据左手定则可知粒子均带负电,故A正确;
BC.根据洛伦兹力提供向心力,则有
可得
由图可确定粒子运动半径关系,粒子的速率与运动半径、粒子的电量、质量有关,由于粒子的速率、粒子的电量、粒子的质量都未知,所以无法确定、粒子的速率的大小关系和、粒子的所带的电荷量关系,故B、C错误;
D.根据可知磁感应强度相同,周期与比荷有关,比荷不确定,无法判定周期关系,故D错误;
故选A。
4.D
【详解】
试题分析:因为粒子的能量逐渐减小而带电量不变.根据半径公式可得粒子的运动半径逐渐减小,即粒子是从a运动到b的,根据可得粒子受到的洛伦兹力减小,根据左手定则,粒子带负电,故D正确;
5.B
【详解】
粒子的半径,穿过粒子运动轨迹内的磁通量,可知:
6.C
【详解】
A.粒子飞入匀强磁场后,不一定做匀速圆周运动,比如若粒子的速度与磁场方向平行,做匀速直线运动,A错误;
B.带电粒子在匀强磁场中做匀速圆周运动,速度的方向时刻改变,则速度一定改变,B错误;
C.带电粒子在匀强磁场中做匀速圆周运动,洛伦兹力的方向与速度方向垂直,C正确;
D.带电粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,指向圆心,向心加速度指向圆心,加速度变化,D错误。
故选C。
7.A
【详解】
A.而电荷在电场中一定受电场力的作用,选项A正确;
B.当电荷在磁场中静止或者速度方向与磁场方向平行时,电荷在磁场中将不受磁场力的作用,选项B错误;
C.正电荷受电场力的方向与该处的电场方向一致,选项C错误;
D.电荷若受磁场力,则由左手定则可知受力方向与该处的磁场方向垂直,选项D错误。
故选A。
8.D
【详解】
试题分析:注意电荷在磁场中受洛伦兹力是“有条件”的即运动电荷和磁场方向有夹角,若是平行或电荷与磁场相对静止则不受洛伦兹力作用,而电荷在电场中受电场力是“无条件”的即电场力与电荷的运动状态无关.
解:A、电场的基本性质就是对其中的电荷有力的作用,电荷运动方向与电场方向平行时,仍然受电场力作用.故A错误;
B、规定正电荷受电场力的方向与该处的电场方向一致,对于负电荷不可以,故B错误
C、电荷在磁场中受洛伦兹力时是有条件的,即运动电荷和磁场方向有夹角,故C错误
D、根据左手定则,电荷所受的洛伦兹力方向一定与磁场方向垂直,故D正确.
故选D
9.B
【详解】
A.电荷在电场中必受电场力,运动电荷在磁场中不一定受洛伦兹力(速度方向和速度方向平行),故A错误;
B.电场线分布的疏密表示电场的强弱,磁感线分布的疏密表示磁场的强弱,故B正确;
C.电场方向与正电荷受电场力方向相同,根据左手定则可知,洛伦兹力方向与磁场方向垂直,故C错误;
D.电场线不闭合,但磁感线是闭合的,故D错误。
故选B。
10.D
【详解】
电子束在磁场中运动,径迹发生了弯曲,这表明运动电荷受到了磁场力,故选项D正确,选项ABC错误.
11.B
【详解】
A.若粒子带正电,则受到的电场力一定向外,则当顺时针转动时,合力向外,粒子不可能做圆周运动,故A错误;
B.根据A的分析可知,粒子一定带负电;根据可知,线速度之比为1:2;由于逆时针转动时,向心力较小,故线速度较小,因此沿逆时针方向旋转时的线速度是沿顺时针方向时的;故B正确;
CD.顺时针转动时,洛伦兹力向里,则有
F库+Bqv1=ma1
而逆时针转动时,洛伦兹力向外
F库-Bqv2=ma2
由于v1=2v2则
a1=4a2
且
则有联立解得
故C错误,D错误;
故选B。
12.B
【详解】
AB.由磁感线的疏密可知,,故B正确,A错误;
CD.由于未说明导线方向与磁场方向的关系,故安培力大小无法判断;静止的电荷在磁场中不受洛伦兹力,故CD错误。
故选B。
13.AB
【详解】
当粒子的速度方向与磁场方向平行,则不受洛伦兹力.粒子做匀速直线运动;
若粒子只受洛伦兹力,由于洛伦兹力不做功,可知速度大小不变,动能不变.
洛伦兹力的方向与电荷的运动方向垂直,粒子做匀速圆周运动,若不垂直,则可能螺旋式曲线运动,故AB正确,CD错误;
故选AB。
14.BD
【详解】
要使荧光屏上的亮线向下,若加电场,则应使电子所受电场力沿z轴负方向,所以电场方向应沿z轴正方向;若加磁场,则应使电子所受洛伦兹力沿z轴负方向,根据左手定则可知磁场方向应沿y轴正方向,故选BD。
15.AC
【详解】
试题分析:磁场向里,负电荷运动方向向右,根据左手定则可得,大拇指方向的反方向即为洛伦兹力,洛伦兹力方向向下,所以A正确;磁场向外,负电荷运动方向向右,根据左手定则可得,大拇指方向的反方向即为洛伦兹力,洛伦兹力方向向上,所以B错误;磁场向里,电流向左,根据左手定则可得,安培力的方向向下,所以C正确;磁场向外,电流向外,它们的方向相同,两者平行,不受安培力的作用,所以D错误.
16. 垂直 磁场 垂直 方向 大小 匀速圆周 洛伦兹
17. 一定 不相等 不相等 相等
【详解】
洛伦兹力的方向由左手定则判定,其方向与磁场方向和运动方向必垂直;它们运动过程中洛伦兹力提供向心力,做匀速圆周运动,由牛顿第二定律知qvB=m,所以圆周运动的半径R=,显然R与电子速率成正比,因为速率v不同,则它们受到的洛伦兹力大小不相等,做圆周运动的半径也不相等;由周期公式T=得T=,显然周期T与速率v无关,所以两电子圆周运动的周期一定相等.
18. α
【详解】
射线是高速流,一个粒子带两个正电荷.根据左手定则,射线受到的洛伦兹力向右,故丙是射线;
射线是高速电子流),质量数为0,带一个负电荷.根据左手定则,β射线受到的洛伦兹力向左,故甲是β射线;
γ射线是γ光子,是电中性的,故在磁场中不受磁场的作用力,轨迹不会发生偏转.故乙是γ射线.
19.
【详解】
粒子在电场中加速.由动能定理得:,得:
带电粒子在磁场中受到的洛伦兹力:
由洛伦兹力提供向心力得:,所以:.
点睛:考查粒子在电场中加速与磁场中偏转,掌握动能定理与牛顿第二定律的应用,注意运动半径与已知长度的关系.
20.4cm
【详解】
电场、磁场都存在,电子做匀速直线运动,则,解得:
单独存在磁场时,电子做匀速圆周运动轨迹如图:
则由几何关系可得:,解得:
又,得
单独存在电场时,电子在电场中做类平抛运动,设偏离距离为,则:
联立各式可得:
21.(1)
(2),,可用薄纸挡去a粒子,须用厚铅板挡掉γ射线.
(3)速率在区间射出的β粒子速宽为,方向水平向右.
(4)由对称性可以设计出如图所示的磁场区域,最后形成聚焦,且方向水平向右.
【详解】
(1)根据带电粒子在磁场中受洛伦磁力作用后作圆周运动的规律
①
由临界条件d、B和的关系为
②
(2)由①式可得a粒子的回旋半径
由②式得
竖直方向的距离为
可见通过区域Ⅰ的磁场难以将a粒子与γ射线分离.可用薄纸挡去a粒子,须用厚铅板挡掉γ射线.
(3)在上述磁场条件下,要求速率在区间的β粒子离开Ⅱ时的位置和方向.先求出速度为的β粒子所对应的圆周运动半径
该β粒子从区域Ⅰ磁场射出时,垂直方向偏离的距离为
同理可得从区域Ⅱ射出时,垂直方向偏离的距离为
同理可得,与速度为对应的β粒子垂直方向偏离的距离为
速率在区间射出的β粒子速宽为,方向水平向右.
(4)由对称性可以设计出如图所示的磁场区域,最后形成聚焦,且方向水平向右.
22.(1)磁场方向垂直纸面向外,;(2);(3)
【详解】
(1)磁场方向垂直纸面向外,有
得
(2)设质点所受电场力为F,所到位置的坐标(x,y),根据动能定理,有
①
质点运动到、位置时,其动能最小,根据动能定理,有
②
半圆形细管道的方程为
③
得
④
(3)如图所示,任意选取运动过程中的某个位置,假设质点在该位置所受管道的弹力N是径向指向圆心,根据牛顿第二定律,有
⑤
利用几何关系
⑥
联立②⑤⑥⑦式,得
⑦
由基本不等式可得的最大值为R,且此位置N>0,所以
⑧
23.(1);
(2)
【详解】
试题分析:(1)设粒子从两圆筒间电场中飞出时速度为v,根据动能定理得:
设粒子在磁场中做匀速圆周运动的轨道半径为r,
解得:
(2)粒子从A点进入磁场,可做出其运动其如图中虚线所示.利用几何关系可算得:
设圆筒角速度为ω为使粒子每次都能从圆筒上的小孔进入电场,则应满足:
由以上各式解得:
答案第1页,共2页
一、选择题(共15题)
1.如图所示,磁感应强度的方向、正电荷运动的方向、洛伦兹力的方向,三者之间关系正确的是( )
A. B. C. D.
2.如下图所示,磁场方向、电荷的运动方向、电荷所受洛伦兹力的方向两两垂直,则正确的是( )
A.B. C. D.
3.在垂直纸面向外的匀强磁场B中,有不计重力的a、b两个带电粒子,在纸面内做匀速圆周运动,运动方向和轨迹示意如图所示。下列说法正确的是( )
A.a、b两粒子所带电性相同
B.a粒子所带的电荷量较大
C.a粒子运动的速率较大
D.a粒子所做圆周运动的周期较长
4.一个带电粒子,沿垂直于磁场方向,射入匀强磁场中,粒子的一段径迹如图所示,径迹上的每一小段都可以近似看成圆弧.由于带电粒子使周围的空气电离,粒子的能量逐渐减小而带电量不变.不计粒子重力,从图中情况可以确定( )
A.粒子是带正电的,它所受的洛仑兹力大小不变
B.粒子是带正电的,它是由a点运动到b点
C.粒子是带负电的,它所受的洛仑兹力大小逐渐增大
D.粒子是带负电的,它是由a点运动到b点
5.一个质量为m、电量为q的粒子,以与匀强磁场B垂直的速度v射入磁场中,仅受洛仑兹力作用,则穿过粒子运动轨迹内的磁通量Φ与磁感应强度B大小的关系是( )
A.Φ∝B B.Φ∝ C.Φ∝B2 D.Φ∝
6.关于带电粒子在匀强磁场中的运动,下列说法正确的是( )
A.带电粒子飞入匀强磁场后,一定做匀速圆周运动
B.带电粒子飞入匀强磁场后做匀速圆周运动时,速度一定不变
C.带电粒子飞入匀强磁场后做匀速圆周运动时,洛伦兹力的方向总和运动方向垂直
D.带电粒子飞入匀强磁场后做匀速圆周运动时,加速度一定保持不变
7.有关电荷所受电场力和洛仑兹力的说法中,正确的是( )
A.电荷在电场中一定受电场力的作用
B.电荷在磁场中一定受磁场力的作用
C.电荷受电场力的方向与该处的电场方向一致
D.电荷若受磁场力,则受力方向与该处的磁场方向不一定垂直
8.关于电荷所受电场力和洛伦兹力,正确的说法是( )
A.电荷运动方向与电场方向平行时,不受电场力作用
B.电荷所受电场力方向一定与该处电场方向相同
C.电荷在磁场中一定受洛伦兹力作用
D.电荷所受的洛伦兹力方向一定与磁场方向垂直
9.电场和磁场的性质既有相似性,又各有其特殊性,下列关于电场和磁场有关性质的比较,正确的是( )
A.电荷在电场中必受电场力,运动电荷在磁场中必受洛伦兹力
B.电场线分布的疏密表示电场的强弱,磁感线分布的疏密表示磁场的强弱
C.电场方向与正电荷受电场力方向相同,磁场方向与正电荷受洛伦兹力方向相同
D.电场线和磁感线都是不闭合的
10.如图所示,当磁铁的磁极靠近阴极射线管时,荧光屏上的亮线发生了弯曲.这个现象说明
A.阴极射线中的粒子带负电
B.阴极射线中的粒子带正电
C.运动电荷的周围存在电场
D.运动电荷受到磁场的作用力
11.如图所示,磁场中固定一个电荷量为Q的正点电荷,一个电荷量为q,质量为m的带电粒子(重力不计)以正点电荷为圆心,在匀强磁场中做匀速圆周运动,测得以不同的绕行方向绕正电荷做半径为r的圆周运动时,周期之比为2:1,已知静电力常量为k,下列说法中正确的是( )
A.粒子可能带正电,以不同的绕行方向做圆周运动时,所受洛伦兹力大小相等
B.粒子一定带负电,且沿逆时针方向旋转时的线速度是沿顺时针方向时的
C.粒子顺时针旋转时,向心加速度大小为
D.粒子逆时针旋转时,向心加速度大小为
12.磁场中某区域的磁感线如图所示,下列说法中正确的是( )
A.a、b两处的磁感应强度大小
B.a、b两处的磁感应强度大小
C.一通电直导线分别放在a、b两处,所受的安培力大小一定有Fa
A.匀速圆周运动 B.匀速直线运动
C.匀加速直线运动 D.平抛运动
14.阴极射线管示意图如图所示。接通电源后,电子流由阴极沿x轴正方向射出,在荧光屏上会看到一条亮线。要使荧光屏上的亮线向下(z轴负方向)偏转,在下列措施中可采用的是( )
A.加一电场,电场方向沿z轴负方向 B.加一电场,电场方向沿z轴正方向
C.加一磁场,磁场方向沿y轴负方向 D.加一磁场,磁场方向沿y轴正方向
15.下面的四个图显示了磁场对通电直导线或运动电荷的作用力,其中正确的是( )
A. B.
C. D.
二、填空题
16.若v⊥B,此时初速度方向、洛伦兹力的方向均与磁场方向______,粒子在垂直于______方向的平面内运动.
(1)洛伦兹力与粒子的运动方向______,只改变粒子速度的______,不改变粒子速度的______.
(2)带电粒子在垂直于磁场的平面内做______运动,______力提供向心力.
17.在某匀强磁场中,有两个电子以不同的速率在做匀速圆周运动.它们受到的洛伦兹力方向____(选填“一定”或“不一定”)跟速度方向垂直;它们受到的洛伦兹力大小一定______,做圆周运动的半径一定______,周期一定____(后三空均选填“相等”或“不相等”).
18.把放射源铀放入用铅做成的容器中,射线只能从容器的小孔射出,在射线经过的空间施加如图所示的匀强磁场,磁场方向垂直于纸面向外.发现射线分裂成三束,已知放射源放出的射线有α、β、γ三种.则乙是______射线,丙是________射线.
19.一初速度为零的带电粒子,经电压为U的电场加速后进入磁感应强度为B的匀强磁场中,已知带电粒子的质量为m,电量为q,则带电粒子所受的洛仑兹力为______,轨道半径为______.
三、综合题
20.在宽L=10cm的区域内,存在着互相垂直的电场和磁场,如图所示.一束荷质比e/m=1.8×1011C/kg的电子以v =1.8×106m/s的速度垂直射入场中而恰好不改变运动方向.若去掉电场,电子穿过磁场区后偏离原方向5cm.那么如果去掉磁场而保持原电场,电子将偏离原方向多远?
21.在一个放射源水平放射出、 和三种射线,垂直射入如图所示磁场.区域Ⅰ和Ⅱ的宽度均为d,各自存在着垂直纸面的匀强磁场,两区域的磁感强度大小B相等,方向相反(粒子运动不考虑相对论效应).
(1)若要筛选出速率大于v1的粒子进入区域Ⅱ,要求磁场宽度d与B和v1的关系.
(2)若B=0.0034T,V1=0.1c(c是光速度),则可得d; 粒子的速率为0.001c,计算和射线离开区域Ⅰ时的距离;并给出去除和射线的方法.
(3)当d满足第(1)小题所给关系时,请给出速率在;区间的粒子离开区域Ⅱ时的位置和方向.
(4)请设计一种方案,能使离开区域Ⅱ的粒子束在右侧聚焦且水平出射.
已知:电子质量, 粒子质量,电子电荷量 ,(时)
22.如图所示,在水平面内固定一个半径为R的半圆形光滑细玻璃管,处于垂直纸面方向的匀强磁场中,磁感应强度大小为B。以管的一端O为坐标原点,以其直径为x轴建立平面直角坐标系。一个质量为m,带电量为+q的小球(小球可视为质点)从O端以一定的初速度入射,在玻璃管内运动时恰好不受玻璃管侧壁的作用力。
(1)判断所加磁场的方向,并求出小球入射的初速度大小;
(2)若撤掉磁场,在水平方向施加一个沿y轴负向的匀强电场,已知小球在玻璃管内运动过程中,动能最小值为入射动能的一半,请写出小球在管内运动的动能Ek随x变化的函数;
(3)在(2)问题的基础上,求小球受到玻璃管侧壁作用力的最小值。
23.如图所示,半径R=0.5m的金属圆筒a内同轴放置一半径稍小的金属圆筒b,筒a外部有平行于圆筒轴线、范围足够大的匀强磁场,磁感应强度B=0.2T.两圆筒之间加有U=150V的电压,使两圆筒间产生强电场.一比荷为q/m=104C/kg的带正电粒子从紧贴b筒的M点由静止释放,经电场加速后,穿过a筒上正对M点的小孔,垂直进入匀强磁场(不计粒子重力).
(1)求带电粒子在磁场中做圆周运动的轨道半径r
(2)若粒子从小孔射出的同时,圆筒a、b以相同的角速度沿逆时针方向绕轴线高速旋转.为使粒子在不碰到圆筒a的情况下,还能返回到出发点M,则圆筒旋转的角速度ω应满足什么条件?(忽略筒旋转引起的磁场变化,不计粒子在两筒间运动的时间)
试卷第1页,共3页
参考答案:
1.C
【详解】
根据左手定则可知;
A.该图中洛伦兹力方向向左,选项A错误;
B.该图中洛伦兹力方向向右,选项B错误;
C.该图中洛伦兹力方向向下,选项C正确;
D.该图中洛伦兹力方向向左,选项D错误;
故选C。
2.D
【详解】
A.根据左手定则,该图中洛伦兹力的方向竖直向下,选项A错误;
B.根据左手定则,该图中洛伦兹力的方向水平向右,选项B错误;
C.根据左手定则,该图中洛伦兹力的方向水平向右,选项C错误;
D.根据左手定则,该图中洛伦兹力的方向垂直纸面向外,选项D正确。
故选D。
3.A
【详解】
A.两粒子均逆时针运动,磁场垂直纸面向外,根据左手定则可知粒子均带负电,故A正确;
BC.根据洛伦兹力提供向心力,则有
可得
由图可确定粒子运动半径关系,粒子的速率与运动半径、粒子的电量、质量有关,由于粒子的速率、粒子的电量、粒子的质量都未知,所以无法确定、粒子的速率的大小关系和、粒子的所带的电荷量关系,故B、C错误;
D.根据可知磁感应强度相同,周期与比荷有关,比荷不确定,无法判定周期关系,故D错误;
故选A。
4.D
【详解】
试题分析:因为粒子的能量逐渐减小而带电量不变.根据半径公式可得粒子的运动半径逐渐减小,即粒子是从a运动到b的,根据可得粒子受到的洛伦兹力减小,根据左手定则,粒子带负电,故D正确;
5.B
【详解】
粒子的半径,穿过粒子运动轨迹内的磁通量,可知:
6.C
【详解】
A.粒子飞入匀强磁场后,不一定做匀速圆周运动,比如若粒子的速度与磁场方向平行,做匀速直线运动,A错误;
B.带电粒子在匀强磁场中做匀速圆周运动,速度的方向时刻改变,则速度一定改变,B错误;
C.带电粒子在匀强磁场中做匀速圆周运动,洛伦兹力的方向与速度方向垂直,C正确;
D.带电粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,指向圆心,向心加速度指向圆心,加速度变化,D错误。
故选C。
7.A
【详解】
A.而电荷在电场中一定受电场力的作用,选项A正确;
B.当电荷在磁场中静止或者速度方向与磁场方向平行时,电荷在磁场中将不受磁场力的作用,选项B错误;
C.正电荷受电场力的方向与该处的电场方向一致,选项C错误;
D.电荷若受磁场力,则由左手定则可知受力方向与该处的磁场方向垂直,选项D错误。
故选A。
8.D
【详解】
试题分析:注意电荷在磁场中受洛伦兹力是“有条件”的即运动电荷和磁场方向有夹角,若是平行或电荷与磁场相对静止则不受洛伦兹力作用,而电荷在电场中受电场力是“无条件”的即电场力与电荷的运动状态无关.
解:A、电场的基本性质就是对其中的电荷有力的作用,电荷运动方向与电场方向平行时,仍然受电场力作用.故A错误;
B、规定正电荷受电场力的方向与该处的电场方向一致,对于负电荷不可以,故B错误
C、电荷在磁场中受洛伦兹力时是有条件的,即运动电荷和磁场方向有夹角,故C错误
D、根据左手定则,电荷所受的洛伦兹力方向一定与磁场方向垂直,故D正确.
故选D
9.B
【详解】
A.电荷在电场中必受电场力,运动电荷在磁场中不一定受洛伦兹力(速度方向和速度方向平行),故A错误;
B.电场线分布的疏密表示电场的强弱,磁感线分布的疏密表示磁场的强弱,故B正确;
C.电场方向与正电荷受电场力方向相同,根据左手定则可知,洛伦兹力方向与磁场方向垂直,故C错误;
D.电场线不闭合,但磁感线是闭合的,故D错误。
故选B。
10.D
【详解】
电子束在磁场中运动,径迹发生了弯曲,这表明运动电荷受到了磁场力,故选项D正确,选项ABC错误.
11.B
【详解】
A.若粒子带正电,则受到的电场力一定向外,则当顺时针转动时,合力向外,粒子不可能做圆周运动,故A错误;
B.根据A的分析可知,粒子一定带负电;根据可知,线速度之比为1:2;由于逆时针转动时,向心力较小,故线速度较小,因此沿逆时针方向旋转时的线速度是沿顺时针方向时的;故B正确;
CD.顺时针转动时,洛伦兹力向里,则有
F库+Bqv1=ma1
而逆时针转动时,洛伦兹力向外
F库-Bqv2=ma2
由于v1=2v2则
a1=4a2
且
则有联立解得
故C错误,D错误;
故选B。
12.B
【详解】
AB.由磁感线的疏密可知,,故B正确,A错误;
CD.由于未说明导线方向与磁场方向的关系,故安培力大小无法判断;静止的电荷在磁场中不受洛伦兹力,故CD错误。
故选B。
13.AB
【详解】
当粒子的速度方向与磁场方向平行,则不受洛伦兹力.粒子做匀速直线运动;
若粒子只受洛伦兹力,由于洛伦兹力不做功,可知速度大小不变,动能不变.
洛伦兹力的方向与电荷的运动方向垂直,粒子做匀速圆周运动,若不垂直,则可能螺旋式曲线运动,故AB正确,CD错误;
故选AB。
14.BD
【详解】
要使荧光屏上的亮线向下,若加电场,则应使电子所受电场力沿z轴负方向,所以电场方向应沿z轴正方向;若加磁场,则应使电子所受洛伦兹力沿z轴负方向,根据左手定则可知磁场方向应沿y轴正方向,故选BD。
15.AC
【详解】
试题分析:磁场向里,负电荷运动方向向右,根据左手定则可得,大拇指方向的反方向即为洛伦兹力,洛伦兹力方向向下,所以A正确;磁场向外,负电荷运动方向向右,根据左手定则可得,大拇指方向的反方向即为洛伦兹力,洛伦兹力方向向上,所以B错误;磁场向里,电流向左,根据左手定则可得,安培力的方向向下,所以C正确;磁场向外,电流向外,它们的方向相同,两者平行,不受安培力的作用,所以D错误.
16. 垂直 磁场 垂直 方向 大小 匀速圆周 洛伦兹
17. 一定 不相等 不相等 相等
【详解】
洛伦兹力的方向由左手定则判定,其方向与磁场方向和运动方向必垂直;它们运动过程中洛伦兹力提供向心力,做匀速圆周运动,由牛顿第二定律知qvB=m,所以圆周运动的半径R=,显然R与电子速率成正比,因为速率v不同,则它们受到的洛伦兹力大小不相等,做圆周运动的半径也不相等;由周期公式T=得T=,显然周期T与速率v无关,所以两电子圆周运动的周期一定相等.
18. α
【详解】
射线是高速流,一个粒子带两个正电荷.根据左手定则,射线受到的洛伦兹力向右,故丙是射线;
射线是高速电子流),质量数为0,带一个负电荷.根据左手定则,β射线受到的洛伦兹力向左,故甲是β射线;
γ射线是γ光子,是电中性的,故在磁场中不受磁场的作用力,轨迹不会发生偏转.故乙是γ射线.
19.
【详解】
粒子在电场中加速.由动能定理得:,得:
带电粒子在磁场中受到的洛伦兹力:
由洛伦兹力提供向心力得:,所以:.
点睛:考查粒子在电场中加速与磁场中偏转,掌握动能定理与牛顿第二定律的应用,注意运动半径与已知长度的关系.
20.4cm
【详解】
电场、磁场都存在,电子做匀速直线运动,则,解得:
单独存在磁场时,电子做匀速圆周运动轨迹如图:
则由几何关系可得:,解得:
又,得
单独存在电场时,电子在电场中做类平抛运动,设偏离距离为,则:
联立各式可得:
21.(1)
(2),,可用薄纸挡去a粒子,须用厚铅板挡掉γ射线.
(3)速率在区间射出的β粒子速宽为,方向水平向右.
(4)由对称性可以设计出如图所示的磁场区域,最后形成聚焦,且方向水平向右.
【详解】
(1)根据带电粒子在磁场中受洛伦磁力作用后作圆周运动的规律
①
由临界条件d、B和的关系为
②
(2)由①式可得a粒子的回旋半径
由②式得
竖直方向的距离为
可见通过区域Ⅰ的磁场难以将a粒子与γ射线分离.可用薄纸挡去a粒子,须用厚铅板挡掉γ射线.
(3)在上述磁场条件下,要求速率在区间的β粒子离开Ⅱ时的位置和方向.先求出速度为的β粒子所对应的圆周运动半径
该β粒子从区域Ⅰ磁场射出时,垂直方向偏离的距离为
同理可得从区域Ⅱ射出时,垂直方向偏离的距离为
同理可得,与速度为对应的β粒子垂直方向偏离的距离为
速率在区间射出的β粒子速宽为,方向水平向右.
(4)由对称性可以设计出如图所示的磁场区域,最后形成聚焦,且方向水平向右.
22.(1)磁场方向垂直纸面向外,;(2);(3)
【详解】
(1)磁场方向垂直纸面向外,有
得
(2)设质点所受电场力为F,所到位置的坐标(x,y),根据动能定理,有
①
质点运动到、位置时,其动能最小,根据动能定理,有
②
半圆形细管道的方程为
③
得
④
(3)如图所示,任意选取运动过程中的某个位置,假设质点在该位置所受管道的弹力N是径向指向圆心,根据牛顿第二定律,有
⑤
利用几何关系
⑥
联立②⑤⑥⑦式,得
⑦
由基本不等式可得的最大值为R,且此位置N>0,所以
⑧
23.(1);
(2)
【详解】
试题分析:(1)设粒子从两圆筒间电场中飞出时速度为v,根据动能定理得:
设粒子在磁场中做匀速圆周运动的轨道半径为r,
解得:
(2)粒子从A点进入磁场,可做出其运动其如图中虚线所示.利用几何关系可算得:
设圆筒角速度为ω为使粒子每次都能从圆筒上的小孔进入电场,则应满足:
由以上各式解得:
答案第1页,共2页
