2021—2022学年苏科版数学八年级下册9.3平行四边形的判定及性质同步练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年苏科版数学八年级下册9.3平行四边形的判定及性质同步练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 188.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 14:04:42 | ||
图片预览




文档简介
八年级数学下册《9-3平行四边形》
一、单选题
1.下列结论正确的是( )
A. 平行四边形是轴对称图形 B. 平行四边形的对角线相等
C. 平行四边形的对边平行且相等 D. 平行四边形的对角互补,邻角相等
2.如图,在四边形ABCD中,∠DAC=∠ACB,要使四边形ABCD成为平行四边形,则应增加的条件不能是( )
A.AD=BC B.OA=OC C.AB=CD D.∠ABC+∠BCD=180°
3.在 ABCD中,O是AC、BD的交点,过点O与AC垂直的直线交边AD于点E,若 ABCD的周长为22cm,则△CDE的周长为( )
A.8cm B.10cm C.11cm D.12cm
4.如图,在 ABCD中,对角线AC、BD相交于点O,若AC=12,BD=8,则AD的长度的取值范围是( )
A.AD>2 B.2<AD<10 C.AD<10 D.AD>10
5.如图,在平行四边形ABCD中,都不一定成立的是( )
①AO=CO;②AC⊥BD;③AD∥BC;④∠CAB=∠CAD.
A.①和④ B.②和③ C.③和④ D.②和④
6.如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
A. ∠ADE=∠CBF B. ∠ABE=∠CDF C. DE=BF D. OE=OF
7.如图,点 E , F 是 ABCD 对角线上两点,在条件①DE=BF;②∠ADE=∠CBF; ③AF=CE;④∠AEB=∠CFD 中,添加一个条件,使四边形 DEBF 是平行四边形,可添加 的条件是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
8.如图,在 ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A.2 B.3 C.4 D.6
二、填空题
9.在四边形ABCD中,AB∥CD , AD∥BC , 如果∠B=50°,则∠D=________.
10.如图,在平行四边形 中, 两点均在对角线 上.要使四边形 为平行四边形,在不添加辅助线的情况下,需要增加的一个条件是________(写出一个即可).
11.如图,AB=AC,四边形AEDF是平行四边形,△CFD和△DEB的周长分别为5和10,则△ABC的周长是 .
12.如图,在平行四边形ABCD中,AB=2,BC=5.∠BCD的平分线交AD于点F,交BA的延长线于点E,则AE的长为 .
13.如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF= .
14.如图,在 ABCD中,E为边BC延长线上一点,且CE=2BC,连接AE、DE.若△ADE的面积为1,则△ABE的面积为 .
三、解答题
15.如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm,求平行四边形ABCD的周长.
16.如图,已知AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.
17.如图,△ABC和△ADE都是等边三角形,点D在BC边上,AB边上有一点F,且BF=DC,连接EF、EB。
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形。
18如图,在 ABCD中,O是BD的中点,E、F分别是BC、AD的中点,M、N分别是OB、OD中点.求证:四边形MENF是平行四边形.
19如图,在□ABCD中,AC交BD于点O , 点E,点F分别是OA,OC的中点。求证:四边形BEDF为平行四边形
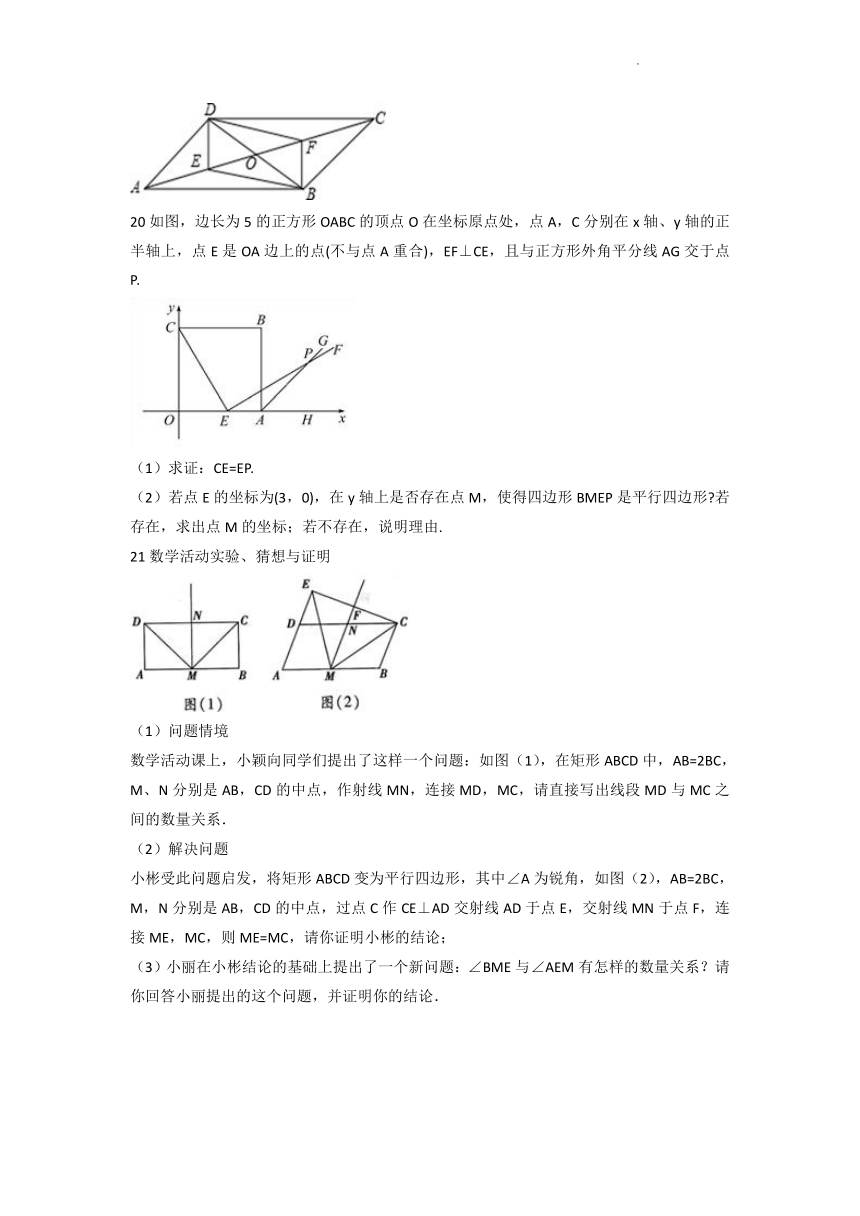
20如图,边长为5的正方形OABC的顶点O在坐标原点处,点A,C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.
(1)求证:CE=EP.
(2)若点E的坐标为(3,0),在y轴上是否存在点M,使得四边形BMEP是平行四边形 若存在,求出点M的坐标;若不存在,说明理由.
21数学活动实验、猜想与证明
(1)问题情境
数学活动课上,小颖向同学们提出了这样一个问题:如图(1),在矩形ABCD中,AB=2BC,M、N分别是AB,CD的中点,作射线MN,连接MD,MC,请直接写出线段MD与MC之间的数量关系.
(2)解决问题
小彬受此问题启发,将矩形ABCD变为平行四边形,其中∠A为锐角,如图(2),AB=2BC,M,N分别是AB,CD的中点,过点C作CE⊥AD交射线AD于点E,交射线MN于点F,连接ME,MC,则ME=MC,请你证明小彬的结论;
(3)小丽在小彬结论的基础上提出了一个新问题:∠BME与∠AEM有怎样的数量关系?请你回答小丽提出的这个问题,并证明你的结论.
1.答案为:C.
2.答案为:C
3.答案为:C
4.答案为:B
5.答案为:D.
6.答案为:C.
7.答案为:B
8.答案为:C.
9答案为: 50°
10.答案为: AE=CF(答案不唯一)
11.答案为:15.
12.:答案为:3.
13:答案为:4.
14.3.
15.解:在平行四边形ABCD中,
∵AB∥CD,∴∠ABC+∠BCD=180°,
∵∠ABE=∠EBC,∠BCE=∠ECD.,
∴∠EBC+∠BCE=90°,
∴∠BEC=90°,
∴BC2=BE2+CE2=122+52=132
∴BC=13cm,
∵AD∥BC,
∴∠AEB=∠EBC,
∴∠AEB=∠ABE,
∴AB=AE,
同理CD=ED,∵AB=CD,
∴AB=AE=CD=ED=0.5BC=6.5cm,
∴平行四边形ABCD的周长=2(AB+BC)=2(6.5+13)=39cm
16.证明:∵BE⊥AD,BE⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
∴△AEB≌△DFC(ASA),
∴BE=CF.
∵BE⊥AD,BE⊥AD,
∴BE∥CF.
∴四边形BECF是平行四边形.
17.解:(1)∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°,
∴∠EAD-∠BAD=∠BAC-∠BAD,即:∠EAB=∠DAC,
∴△ABE≌△ACD(SAS);
(2)证明:∵△ABE≌△ACD,∴BE=DC,∠EBA=∠DCA,
又∵BF=DC,∴BE=BF.
∵△ABC是等边三角形,∴∠DCA=60°,
∴△BEF为等边三角形.∴∠EFB=60°,EF=BF
∵△ABC是等边三角形,∴∠ABC=60°,
∴∠ABC=∠EFB,∴EF∥BC,即EF∥DC,
∵EF=BF,BF=DC,∴EF=DC,
∴四边形EFCD是平行四边形。
18.【答案】 证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠FDN=∠EBM,
∵E、F分别是BC、AD的中点,
∴DF=BE,
∵O是BD的中点,
∴OD=OB,
∵M、N分别是OB、OD中点,
∴DN=BM,
在△DNF和△BME中,
,
∴△DNF≌△BME(SAS),
∴FN=EM,∠DNF=∠BME,
∴∠FNM=∠EMN,
∴FN∥EM,
∴四边形MENF是平行四边形.
19【答案】 证明:∵四边形ABCD是平行四边形
∴AO=CO,BO=DO .
又∵点E,点F分别是OA,OC的中点
∴EO= ,FO=
∴EO=FO
∴四边形BEDF为平行四边形
20【答案】 (1)证明:在OC上截取OK=OE.连接EK,如图1.
∵OC=OA,∠COA=∠BA0=90°,∠OEK=∠OKE=45°.
∵AP为正方形OCBA的外角平分线,∴∠BAP=45°,∴∠EKC=∠PAE=135°,∴CK=EA.
∵EC⊥EP,∴∠CEF=∠COE=90°,
∴∠CEO+∠KCE=90°,∠CEO+∠PEA=90°,∴∠KCE=∠CEA.
在△CKE和△EAP中,∵ ,
∴△CKE≌△EAP,∴EC=EP;
(2)解:y轴上存在点M,使得四边形BMEP是平行四边形.
如图,过点B作BM∥PE交y轴于点M,连接BP,EM,如图2,
则∠CQB=∠CEP=90°,所以∠OCE=∠CBQ.
在△BCM和△COE中,∵ ,
∴△BCM≌△COE,∴BM=CE.
∵CE=EP,∴BM=EP.
∵BM∥EP,∴四边形BMEP是平行四边形.
∵△BCM≌△COE,∴CM=OE=3,∴OM=CO﹣CM=2.
故点M的坐标为(0,2).
21.【答案】 (1)MD=MC
∵四边形ABCD为矩形
∴AD=BC,∠A=∠B=90°
∵点M为AB的中点
∴AM=BM
在△AMD和△BMC中
∴△AMD≌△BMC
∴MD=MC
(2)∵M,N分别是AB,CD的中点,
∴AM=BM,CN=DN
∵四边形ABCD为平行四边形
∴AB∥CD,AB=CD
∴AM=BM= CN=DN
∴四边形AMND和四边形MBCN为平行四边形
∴AD∥MN
∴
∴CF=EF
∵CE⊥AD
∴CE⊥MN
∴MN垂直平分CE
∴ME=MC
(3)∠BME=3∠AEM,证明如下:
∵四边形AMND和四边形MBCN为平行四边形
∴AD∥MN∥BC,CF∥BM,MN=BC
∴∠AEM=∠EMF,∠NCM=∠BMC
∵AB=2BC,AB=CD=2CF
∴CF=MN
∴∠NCM=∠NMC
∴∠BMC=∠NMC
∵ME=MC,MF⊥CE
∴∠EMF=∠NMC
∴∠BME=∠EMF+∠NMC+∠BMC=3∠EMF=3∠AEM
即∠BME=3∠AEM
一、单选题
1.下列结论正确的是( )
A. 平行四边形是轴对称图形 B. 平行四边形的对角线相等
C. 平行四边形的对边平行且相等 D. 平行四边形的对角互补,邻角相等
2.如图,在四边形ABCD中,∠DAC=∠ACB,要使四边形ABCD成为平行四边形,则应增加的条件不能是( )
A.AD=BC B.OA=OC C.AB=CD D.∠ABC+∠BCD=180°
3.在 ABCD中,O是AC、BD的交点,过点O与AC垂直的直线交边AD于点E,若 ABCD的周长为22cm,则△CDE的周长为( )
A.8cm B.10cm C.11cm D.12cm
4.如图,在 ABCD中,对角线AC、BD相交于点O,若AC=12,BD=8,则AD的长度的取值范围是( )
A.AD>2 B.2<AD<10 C.AD<10 D.AD>10
5.如图,在平行四边形ABCD中,都不一定成立的是( )
①AO=CO;②AC⊥BD;③AD∥BC;④∠CAB=∠CAD.
A.①和④ B.②和③ C.③和④ D.②和④
6.如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
A. ∠ADE=∠CBF B. ∠ABE=∠CDF C. DE=BF D. OE=OF
7.如图,点 E , F 是 ABCD 对角线上两点,在条件①DE=BF;②∠ADE=∠CBF; ③AF=CE;④∠AEB=∠CFD 中,添加一个条件,使四边形 DEBF 是平行四边形,可添加 的条件是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
8.如图,在 ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )
A.2 B.3 C.4 D.6
二、填空题
9.在四边形ABCD中,AB∥CD , AD∥BC , 如果∠B=50°,则∠D=________.
10.如图,在平行四边形 中, 两点均在对角线 上.要使四边形 为平行四边形,在不添加辅助线的情况下,需要增加的一个条件是________(写出一个即可).
11.如图,AB=AC,四边形AEDF是平行四边形,△CFD和△DEB的周长分别为5和10,则△ABC的周长是 .
12.如图,在平行四边形ABCD中,AB=2,BC=5.∠BCD的平分线交AD于点F,交BA的延长线于点E,则AE的长为 .
13.如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF= .
14.如图,在 ABCD中,E为边BC延长线上一点,且CE=2BC,连接AE、DE.若△ADE的面积为1,则△ABE的面积为 .
三、解答题
15.如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm,求平行四边形ABCD的周长.
16.如图,已知AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.
17.如图,△ABC和△ADE都是等边三角形,点D在BC边上,AB边上有一点F,且BF=DC,连接EF、EB。
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形。
18如图,在 ABCD中,O是BD的中点,E、F分别是BC、AD的中点,M、N分别是OB、OD中点.求证:四边形MENF是平行四边形.
19如图,在□ABCD中,AC交BD于点O , 点E,点F分别是OA,OC的中点。求证:四边形BEDF为平行四边形
20如图,边长为5的正方形OABC的顶点O在坐标原点处,点A,C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.
(1)求证:CE=EP.
(2)若点E的坐标为(3,0),在y轴上是否存在点M,使得四边形BMEP是平行四边形 若存在,求出点M的坐标;若不存在,说明理由.
21数学活动实验、猜想与证明
(1)问题情境
数学活动课上,小颖向同学们提出了这样一个问题:如图(1),在矩形ABCD中,AB=2BC,M、N分别是AB,CD的中点,作射线MN,连接MD,MC,请直接写出线段MD与MC之间的数量关系.
(2)解决问题
小彬受此问题启发,将矩形ABCD变为平行四边形,其中∠A为锐角,如图(2),AB=2BC,M,N分别是AB,CD的中点,过点C作CE⊥AD交射线AD于点E,交射线MN于点F,连接ME,MC,则ME=MC,请你证明小彬的结论;
(3)小丽在小彬结论的基础上提出了一个新问题:∠BME与∠AEM有怎样的数量关系?请你回答小丽提出的这个问题,并证明你的结论.
1.答案为:C.
2.答案为:C
3.答案为:C
4.答案为:B
5.答案为:D.
6.答案为:C.
7.答案为:B
8.答案为:C.
9答案为: 50°
10.答案为: AE=CF(答案不唯一)
11.答案为:15.
12.:答案为:3.
13:答案为:4.
14.3.
15.解:在平行四边形ABCD中,
∵AB∥CD,∴∠ABC+∠BCD=180°,
∵∠ABE=∠EBC,∠BCE=∠ECD.,
∴∠EBC+∠BCE=90°,
∴∠BEC=90°,
∴BC2=BE2+CE2=122+52=132
∴BC=13cm,
∵AD∥BC,
∴∠AEB=∠EBC,
∴∠AEB=∠ABE,
∴AB=AE,
同理CD=ED,∵AB=CD,
∴AB=AE=CD=ED=0.5BC=6.5cm,
∴平行四边形ABCD的周长=2(AB+BC)=2(6.5+13)=39cm
16.证明:∵BE⊥AD,BE⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
∴△AEB≌△DFC(ASA),
∴BE=CF.
∵BE⊥AD,BE⊥AD,
∴BE∥CF.
∴四边形BECF是平行四边形.
17.解:(1)∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°,
∴∠EAD-∠BAD=∠BAC-∠BAD,即:∠EAB=∠DAC,
∴△ABE≌△ACD(SAS);
(2)证明:∵△ABE≌△ACD,∴BE=DC,∠EBA=∠DCA,
又∵BF=DC,∴BE=BF.
∵△ABC是等边三角形,∴∠DCA=60°,
∴△BEF为等边三角形.∴∠EFB=60°,EF=BF
∵△ABC是等边三角形,∴∠ABC=60°,
∴∠ABC=∠EFB,∴EF∥BC,即EF∥DC,
∵EF=BF,BF=DC,∴EF=DC,
∴四边形EFCD是平行四边形。
18.【答案】 证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠FDN=∠EBM,
∵E、F分别是BC、AD的中点,
∴DF=BE,
∵O是BD的中点,
∴OD=OB,
∵M、N分别是OB、OD中点,
∴DN=BM,
在△DNF和△BME中,
,
∴△DNF≌△BME(SAS),
∴FN=EM,∠DNF=∠BME,
∴∠FNM=∠EMN,
∴FN∥EM,
∴四边形MENF是平行四边形.
19【答案】 证明:∵四边形ABCD是平行四边形
∴AO=CO,BO=DO .
又∵点E,点F分别是OA,OC的中点
∴EO= ,FO=
∴EO=FO
∴四边形BEDF为平行四边形
20【答案】 (1)证明:在OC上截取OK=OE.连接EK,如图1.
∵OC=OA,∠COA=∠BA0=90°,∠OEK=∠OKE=45°.
∵AP为正方形OCBA的外角平分线,∴∠BAP=45°,∴∠EKC=∠PAE=135°,∴CK=EA.
∵EC⊥EP,∴∠CEF=∠COE=90°,
∴∠CEO+∠KCE=90°,∠CEO+∠PEA=90°,∴∠KCE=∠CEA.
在△CKE和△EAP中,∵ ,
∴△CKE≌△EAP,∴EC=EP;
(2)解:y轴上存在点M,使得四边形BMEP是平行四边形.
如图,过点B作BM∥PE交y轴于点M,连接BP,EM,如图2,
则∠CQB=∠CEP=90°,所以∠OCE=∠CBQ.
在△BCM和△COE中,∵ ,
∴△BCM≌△COE,∴BM=CE.
∵CE=EP,∴BM=EP.
∵BM∥EP,∴四边形BMEP是平行四边形.
∵△BCM≌△COE,∴CM=OE=3,∴OM=CO﹣CM=2.
故点M的坐标为(0,2).
21.【答案】 (1)MD=MC
∵四边形ABCD为矩形
∴AD=BC,∠A=∠B=90°
∵点M为AB的中点
∴AM=BM
在△AMD和△BMC中
∴△AMD≌△BMC
∴MD=MC
(2)∵M,N分别是AB,CD的中点,
∴AM=BM,CN=DN
∵四边形ABCD为平行四边形
∴AB∥CD,AB=CD
∴AM=BM= CN=DN
∴四边形AMND和四边形MBCN为平行四边形
∴AD∥MN
∴
∴CF=EF
∵CE⊥AD
∴CE⊥MN
∴MN垂直平分CE
∴ME=MC
(3)∠BME=3∠AEM,证明如下:
∵四边形AMND和四边形MBCN为平行四边形
∴AD∥MN∥BC,CF∥BM,MN=BC
∴∠AEM=∠EMF,∠NCM=∠BMC
∵AB=2BC,AB=CD=2CF
∴CF=MN
∴∠NCM=∠NMC
∴∠BMC=∠NMC
∵ME=MC,MF⊥CE
∴∠EMF=∠NMC
∴∠BME=∠EMF+∠NMC+∠BMC=3∠EMF=3∠AEM
即∠BME=3∠AEM
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
