2021-2022学年苏科版数学九年级下册6.4探索三角形相似的条件同步练习卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学九年级下册6.4探索三角形相似的条件同步练习卷(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 155.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 14:04:45 | ||
图片预览


文档简介
6.4《探索三角形相似的条件》
一、选择题
1、下列两个三角形不一定相似的是( )
A.两条直角边的比都是2:3的两个直角三角形 B.腰与底的比都是2:3的两个等腰三角形
C.有一个内角为50°的两个直角三角形 D.有一个内角是50°的两个等腰三角形
2、已知△ABC是正三角形,点D是边BC上一动点(不与A、C重合),以BD为边作正△BDE,边DE与边AB交于点F,则图中一定相似的三角形有( )对.
A.6 B.5 C.4 D.3
3在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有( )
A.ΔADE∽ΔAEF B.ΔECF∽ΔAEF C.ΔADE∽ΔECF D.ΔAEF∽ΔABF
4.如图所示,在 ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形有( )
A.3对 B.4对 C.5对 D.6对
5.如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是( )
A.△PAB∽△PCA B.△PAB∽△PDA C.△ABC∽△DBA D.△ABC∽△DCA
6.如图,AB∥CD∥EF,则图中相似三角形的对数是( )
A.1 B.2 C.3 D.4
7、如图,在△ABC中,点P在边AB上,则在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;
③AC2=AP AB;④AB CP=AP CB,能满足△APC与△ACB相似的条件是( )
A.①②④ B.①③④ C.②③④ D.①②③
8、如图,正方形ABCD的边长为4,延长CB至E使EB=2,以EB为边在上方作正方形EFGB,延长FG交DC于M,连接AM,AF,H为AD的中点,连接FH分别与AB,AM交于点N,K:
则下列结论:①△ANH≌△GNF;②∠AFN=∠HFG;③FN=2NK;④S△AFN∶S△ADM=1∶4.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,在△ABC中,∠A=90°,∠C=30°,N是AB的中点,MN⊥BC于点M,则△BMN∽△ ,相似比为 .
10.如图,点D,E分别在△ABC的AB,AC边上.只需添加一个条件即可证明△ADE∽△ACB,这个条件可以是 .(写出一个即可)
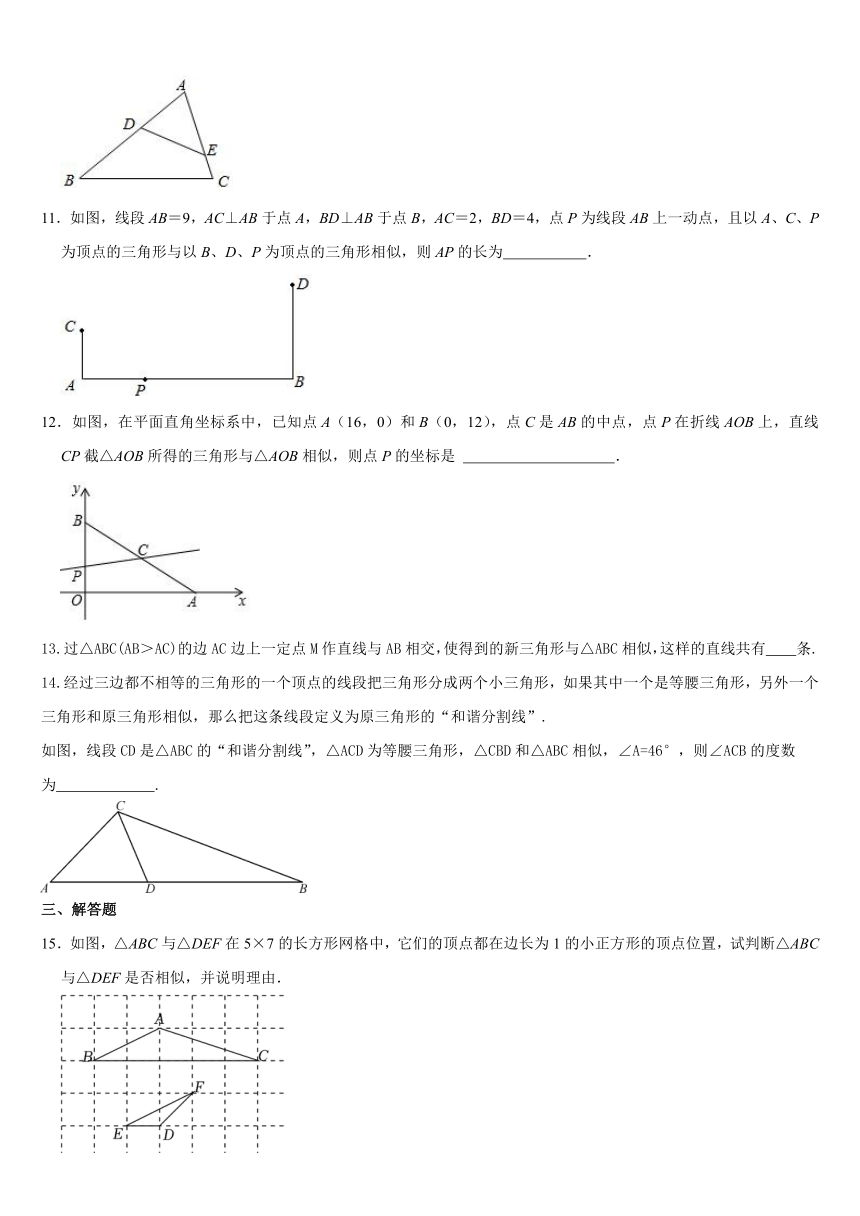
11.如图,线段AB=9,AC⊥AB于点A,BD⊥AB于点B,AC=2,BD=4,点P为线段AB上一动点,且以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似,则AP的长为 .
12.如图,在平面直角坐标系中,已知点A(16,0)和B(0,12),点C是AB的中点,点P在折线AOB上,直线CP截△AOB所得的三角形与△AOB相似,则点P的坐标是 .
13.过△ABC(AB>AC)的边AC边上一定点M作直线与AB相交,使得到的新三角形与△ABC相似,这样的直线共有 条.
14.经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.
如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为 .
三、解答题
15.如图,△ABC与△DEF在5×7的长方形网格中,它们的顶点都在边长为1的小正方形的顶点位置,试判断△ABC与△DEF是否相似,并说明理由.
16.如图,AB⊥BD,CD⊥BD,AB=12,CD=8,BD=28,点P在BD上移动,当以P,C,D为顶点的三角形与△ABP相似时,求PB的长.
17.如图,已知∠BAC=∠EAD,AB=24,AC=48,AE=17,AD=34,求证:△ABC∽△AED.
18如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与AC·CD的大小关系;
(2)试说明△ABC∽△BDC.
参考答案
1.D
2.B
3.C
4.D
5.C
6.C
7.D
8.C
9.BAC;1:4.
10.∠ADE=∠C(答案不唯一).
11.1或3或8.
12.(0,6)、(8,0)、(,0).
13.答案为:2.
14.答案为:113°或92°.
15.解:相似.
理由如下:
∵AB==,BC=5,AC==,DE=1,EF==,DF=,
∴=,==,==,
∴==,
∴△ABC∽△DEF.
16.解:设DP=x,则BP=BD﹣x=28﹣x,
∵AB⊥BD于B,CD⊥BD于D,
∴∠B=∠D=90°,
∴当=时,△ABP∽△CDP,即=,
解得x=,
经检验x=是分式方程的解,
BP=28﹣=16.8;
当=时,△ABP∽△PDC,即=,
解得x1=4,x2=24,
经检验,x=4或24是分式方程的解,
BP=28﹣4=24,BP=28﹣24=4,
∴当BP为16.8或4或24时,以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似.
17.证明:∵AB=24,AC=48,AE=17,AD=34,
∴==,
∴=,
∵∠BAC=∠EAD,
∴△BAC∽△EAD.
18.解:(1)AD2=AC·CD (2)略
一、选择题
1、下列两个三角形不一定相似的是( )
A.两条直角边的比都是2:3的两个直角三角形 B.腰与底的比都是2:3的两个等腰三角形
C.有一个内角为50°的两个直角三角形 D.有一个内角是50°的两个等腰三角形
2、已知△ABC是正三角形,点D是边BC上一动点(不与A、C重合),以BD为边作正△BDE,边DE与边AB交于点F,则图中一定相似的三角形有( )对.
A.6 B.5 C.4 D.3
3在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有( )
A.ΔADE∽ΔAEF B.ΔECF∽ΔAEF C.ΔADE∽ΔECF D.ΔAEF∽ΔABF
4.如图所示,在 ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形有( )
A.3对 B.4对 C.5对 D.6对
5.如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是( )
A.△PAB∽△PCA B.△PAB∽△PDA C.△ABC∽△DBA D.△ABC∽△DCA
6.如图,AB∥CD∥EF,则图中相似三角形的对数是( )
A.1 B.2 C.3 D.4
7、如图,在△ABC中,点P在边AB上,则在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;
③AC2=AP AB;④AB CP=AP CB,能满足△APC与△ACB相似的条件是( )
A.①②④ B.①③④ C.②③④ D.①②③
8、如图,正方形ABCD的边长为4,延长CB至E使EB=2,以EB为边在上方作正方形EFGB,延长FG交DC于M,连接AM,AF,H为AD的中点,连接FH分别与AB,AM交于点N,K:
则下列结论:①△ANH≌△GNF;②∠AFN=∠HFG;③FN=2NK;④S△AFN∶S△ADM=1∶4.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,在△ABC中,∠A=90°,∠C=30°,N是AB的中点,MN⊥BC于点M,则△BMN∽△ ,相似比为 .
10.如图,点D,E分别在△ABC的AB,AC边上.只需添加一个条件即可证明△ADE∽△ACB,这个条件可以是 .(写出一个即可)
11.如图,线段AB=9,AC⊥AB于点A,BD⊥AB于点B,AC=2,BD=4,点P为线段AB上一动点,且以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似,则AP的长为 .
12.如图,在平面直角坐标系中,已知点A(16,0)和B(0,12),点C是AB的中点,点P在折线AOB上,直线CP截△AOB所得的三角形与△AOB相似,则点P的坐标是 .
13.过△ABC(AB>AC)的边AC边上一定点M作直线与AB相交,使得到的新三角形与△ABC相似,这样的直线共有 条.
14.经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.
如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为 .
三、解答题
15.如图,△ABC与△DEF在5×7的长方形网格中,它们的顶点都在边长为1的小正方形的顶点位置,试判断△ABC与△DEF是否相似,并说明理由.
16.如图,AB⊥BD,CD⊥BD,AB=12,CD=8,BD=28,点P在BD上移动,当以P,C,D为顶点的三角形与△ABP相似时,求PB的长.
17.如图,已知∠BAC=∠EAD,AB=24,AC=48,AE=17,AD=34,求证:△ABC∽△AED.
18如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与AC·CD的大小关系;
(2)试说明△ABC∽△BDC.
参考答案
1.D
2.B
3.C
4.D
5.C
6.C
7.D
8.C
9.BAC;1:4.
10.∠ADE=∠C(答案不唯一).
11.1或3或8.
12.(0,6)、(8,0)、(,0).
13.答案为:2.
14.答案为:113°或92°.
15.解:相似.
理由如下:
∵AB==,BC=5,AC==,DE=1,EF==,DF=,
∴=,==,==,
∴==,
∴△ABC∽△DEF.
16.解:设DP=x,则BP=BD﹣x=28﹣x,
∵AB⊥BD于B,CD⊥BD于D,
∴∠B=∠D=90°,
∴当=时,△ABP∽△CDP,即=,
解得x=,
经检验x=是分式方程的解,
BP=28﹣=16.8;
当=时,△ABP∽△PDC,即=,
解得x1=4,x2=24,
经检验,x=4或24是分式方程的解,
BP=28﹣4=24,BP=28﹣24=4,
∴当BP为16.8或4或24时,以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似.
17.证明:∵AB=24,AC=48,AE=17,AD=34,
∴==,
∴=,
∵∠BAC=∠EAD,
∴△BAC∽△EAD.
18.解:(1)AD2=AC·CD (2)略
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
