2021—2022学年苏科版八年级数学下册9.2中心对称与中心对称图形培优训练(Word版含答案)
文档属性
| 名称 | 2021—2022学年苏科版八年级数学下册9.2中心对称与中心对称图形培优训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 323.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 14:10:33 | ||
图片预览



文档简介
9.2中心对称与中心对称图形-苏科版八年级数学下册 培优训练
一、选择题
1、下列四个图案中,是中心对称图形,但不是轴对称图形的是( )
A. B. C. D.
2、在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是( )
A.(2,3) B.(-3,2) C.(-3,-2) D.(-2,-3)
3.如下是一种电子记分牌呈现的数字图形,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形.若点A的坐标是(1,3),则点M和点N的坐标分别是 ( )
A.M(1,-3),N(-1.-3) B.M(-1,-3),N(-1.3)
C.M(-1,-3),N(1.-3) D.M(-1,3),N(1.-3)
5、如图,△ABC与△A′B′C′关于点O中心对称,下列结论中不一定成立的是( )
A.∠ABC=∠A′C′B′ B.OA=OA′ C.BC=B′C′ D.OC=OC
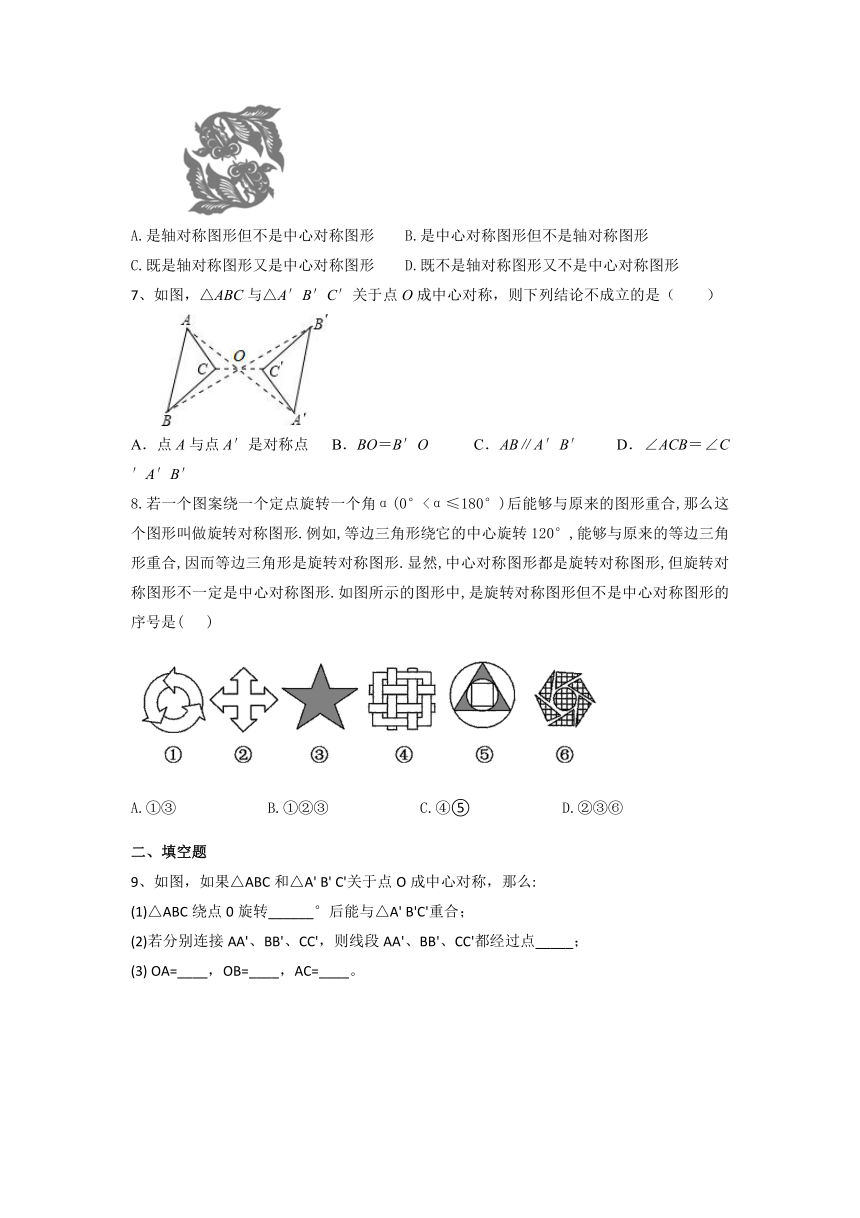
6、剪纸是我国最古老的民间艺术之一,被列入第四批《人类非物质文化遗产代表作名录》,如图所示的剪纸图案( )
A.是轴对称图形但不是中心对称图形 B.是中心对称图形但不是轴对称图形
C.既是轴对称图形又是中心对称图形 D.既不是轴对称图形又不是中心对称图形
7、如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A′是对称点 B.BO=B′O C.AB∥A′B′ D.∠ACB=∠C′A′B′
8.若一个图案绕一个定点旋转一个角α(0°<α≤180°)后能够与原来的图形重合,那么这个图形叫做旋转对称图形.例如,等边三角形绕它的中心旋转120°,能够与原来的等边三角形重合,因而等边三角形是旋转对称图形.显然,中心对称图形都是旋转对称图形,但旋转对称图形不一定是中心对称图形.如图所示的图形中,是旋转对称图形但不是中心对称图形的序号是( )
A.①③ B.①②③ C.④⑤ D.②③⑥
二、填空题
9、如图,如果△ABC和△A' B' C'关于点O成中心对称,那么:
(1)△ABC绕点0旋转______°后能与△A' B'C'重合;
(2)若分别连接AA'、BB'、CC',则线段AA'、BB'、CC'都经过点_____;
(3) OA=____,OB=____,AC=____。
10.六张完全相同的卡片上,分别画有等边三角形、正方形、矩形、平行四边形、圆、菱形,现从中随机抽取一张,卡片上画的恰好既是轴对称图形又是中心对称图形的概率为________.
11.如图,如果△ABC和△DEF关于点G成中心对称,那么△ABC绕点G旋转________°后能与△DEF重合.
12.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为________.
13.如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为________.
14若一个图案绕一个定点旋转一个角α(0°<α≤180°)后能够与原来的图形重合,那么这个图形叫做旋转对称图形.例如,等边三角形绕它的中心旋转120°,能够与原来的等边三角形重合,因而等边三角形是旋转对称图形.显然,中心对称图形都是旋转对称图形,但旋转对称图形不一定是中心对称图形.如图所示的图形中,是旋转对称图形但不是中心对称图形的序号是____________
三、解答题
15.如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣4,2)、B(0,4)、C(0,2),
(1)画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
16.如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .
17.△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点A逆时针旋转90°得到△A2B2C2,
(2)回答下列问题:
①△A1B1C1中顶点A1坐标为 ;
②若P(a,b)为△ABC内的一点,则按照(1)中①作图,点P对应的点P1的坐标为 .
18、如图,正方形ABCD与正方形A1B1C1D1关于某点成中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
19.如图,正方形ABCD于正方形A1B1C1D1关于某点中心对称,已知A,D1 , D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标.
(2)写出顶点B,C,B1 , C1的坐标.
1、 2、C 3、C 4、B 5、A 6、B 7、D 8、B
9、(1)180 (2)O (3)OA’;OB’;A’C’
10...
11.180.
12.4.
13..6.
14、①③
15.解:(1)△A1B1C如图所示,△A2B2C2如图所示;
(2)如图,对称中心为(2,﹣1).
16.解:(1)点A关于x轴对称的点坐标为 (-1,-3)
点B关于y轴对称的点坐标为 (-2,0)
点C关于原点对称的点坐标为 (3, 1)
(2)△ABC的面积是9
17.解:(1)如图所示: (2)① (1,-2)② (-a,-b)
18、如图,正方形ABCD与正方形A1B1C1D1关于某点成中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
解:(1)∵正方形ABCD与正方形A1B1C1D1关于某点成中心对称,
∴D,D1是对应点,∴DD1的中点是对称中心.
∵D(0,2),D1(0,3),∴对称中心的坐标为(0,2.5).
(2)B(-2,4),C(-2,2),B1(2,1),C1(2,3).
19 【答案】 解:(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1 , D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B,C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1 , C1的坐标分别是(2,1),(2,3),
综上,可得
顶点B,C,B1 , C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).
一、选择题
1、下列四个图案中,是中心对称图形,但不是轴对称图形的是( )
A. B. C. D.
2、在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是( )
A.(2,3) B.(-3,2) C.(-3,-2) D.(-2,-3)
3.如下是一种电子记分牌呈现的数字图形,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形.若点A的坐标是(1,3),则点M和点N的坐标分别是 ( )
A.M(1,-3),N(-1.-3) B.M(-1,-3),N(-1.3)
C.M(-1,-3),N(1.-3) D.M(-1,3),N(1.-3)
5、如图,△ABC与△A′B′C′关于点O中心对称,下列结论中不一定成立的是( )
A.∠ABC=∠A′C′B′ B.OA=OA′ C.BC=B′C′ D.OC=OC
6、剪纸是我国最古老的民间艺术之一,被列入第四批《人类非物质文化遗产代表作名录》,如图所示的剪纸图案( )
A.是轴对称图形但不是中心对称图形 B.是中心对称图形但不是轴对称图形
C.既是轴对称图形又是中心对称图形 D.既不是轴对称图形又不是中心对称图形
7、如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A′是对称点 B.BO=B′O C.AB∥A′B′ D.∠ACB=∠C′A′B′
8.若一个图案绕一个定点旋转一个角α(0°<α≤180°)后能够与原来的图形重合,那么这个图形叫做旋转对称图形.例如,等边三角形绕它的中心旋转120°,能够与原来的等边三角形重合,因而等边三角形是旋转对称图形.显然,中心对称图形都是旋转对称图形,但旋转对称图形不一定是中心对称图形.如图所示的图形中,是旋转对称图形但不是中心对称图形的序号是( )
A.①③ B.①②③ C.④⑤ D.②③⑥
二、填空题
9、如图,如果△ABC和△A' B' C'关于点O成中心对称,那么:
(1)△ABC绕点0旋转______°后能与△A' B'C'重合;
(2)若分别连接AA'、BB'、CC',则线段AA'、BB'、CC'都经过点_____;
(3) OA=____,OB=____,AC=____。
10.六张完全相同的卡片上,分别画有等边三角形、正方形、矩形、平行四边形、圆、菱形,现从中随机抽取一张,卡片上画的恰好既是轴对称图形又是中心对称图形的概率为________.
11.如图,如果△ABC和△DEF关于点G成中心对称,那么△ABC绕点G旋转________°后能与△DEF重合.
12.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为________.
13.如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为________.
14若一个图案绕一个定点旋转一个角α(0°<α≤180°)后能够与原来的图形重合,那么这个图形叫做旋转对称图形.例如,等边三角形绕它的中心旋转120°,能够与原来的等边三角形重合,因而等边三角形是旋转对称图形.显然,中心对称图形都是旋转对称图形,但旋转对称图形不一定是中心对称图形.如图所示的图形中,是旋转对称图形但不是中心对称图形的序号是____________
三、解答题
15.如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣4,2)、B(0,4)、C(0,2),
(1)画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
16.如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .
17.△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点A逆时针旋转90°得到△A2B2C2,
(2)回答下列问题:
①△A1B1C1中顶点A1坐标为 ;
②若P(a,b)为△ABC内的一点,则按照(1)中①作图,点P对应的点P1的坐标为 .
18、如图,正方形ABCD与正方形A1B1C1D1关于某点成中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
19.如图,正方形ABCD于正方形A1B1C1D1关于某点中心对称,已知A,D1 , D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标.
(2)写出顶点B,C,B1 , C1的坐标.
1、 2、C 3、C 4、B 5、A 6、B 7、D 8、B
9、(1)180 (2)O (3)OA’;OB’;A’C’
10...
11.180.
12.4.
13..6.
14、①③
15.解:(1)△A1B1C如图所示,△A2B2C2如图所示;
(2)如图,对称中心为(2,﹣1).
16.解:(1)点A关于x轴对称的点坐标为 (-1,-3)
点B关于y轴对称的点坐标为 (-2,0)
点C关于原点对称的点坐标为 (3, 1)
(2)△ABC的面积是9
17.解:(1)如图所示: (2)① (1,-2)② (-a,-b)
18、如图,正方形ABCD与正方形A1B1C1D1关于某点成中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
解:(1)∵正方形ABCD与正方形A1B1C1D1关于某点成中心对称,
∴D,D1是对应点,∴DD1的中点是对称中心.
∵D(0,2),D1(0,3),∴对称中心的坐标为(0,2.5).
(2)B(-2,4),C(-2,2),B1(2,1),C1(2,3).
19 【答案】 解:(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1 , D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B,C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1 , C1的坐标分别是(2,1),(2,3),
综上,可得
顶点B,C,B1 , C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
