2.6.1双曲线的标准方程 课件-2021-2022学年高二数学人教B版(2019)选择性必修第一册(共20张PPT)
文档属性
| 名称 | 2.6.1双曲线的标准方程 课件-2021-2022学年高二数学人教B版(2019)选择性必修第一册(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
双曲线的标准方程
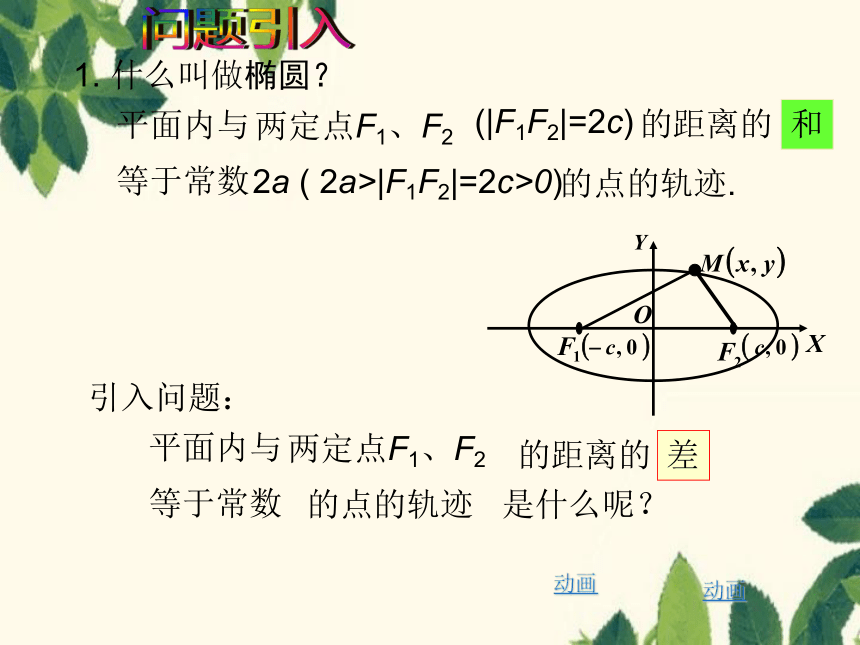
1. 什么叫做椭圆?
两定点F1、F2
(|F1F2|=2c)
和
的距离的
等于常数
2a
( 2a>|F1F2|=2c>0)
的点的轨迹.
平面内与
引入问题:
两定点F1、F2
差
的距离的
等于常数
的点的轨迹 是什么呢?
平面内与
问题引入
动画
动画
小组合作作图
演示实验
几何画板动画演示
分别说出这两条曲线上点满足的条件?
双曲线的定义
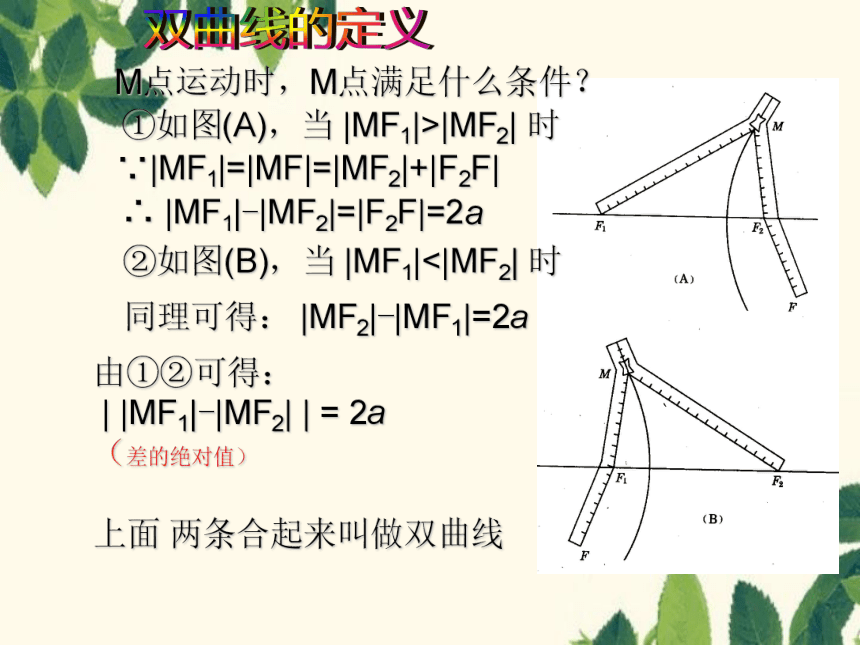
M点运动时,M点满足什么条件?
∵|MF1|=|MF|=|MF2|+|F2F|
①如图(A),当 |MF1|>|MF2| 时
∴ |MF1|-|MF2|=|F2F|=2a
②如图(B),当 |MF1|<|MF2| 时
同理可得: |MF2|-|MF1|=2a
上面 两条合起来叫做双曲线
由①②可得:
| |MF1|-|MF2| | = 2a
(差的绝对值)
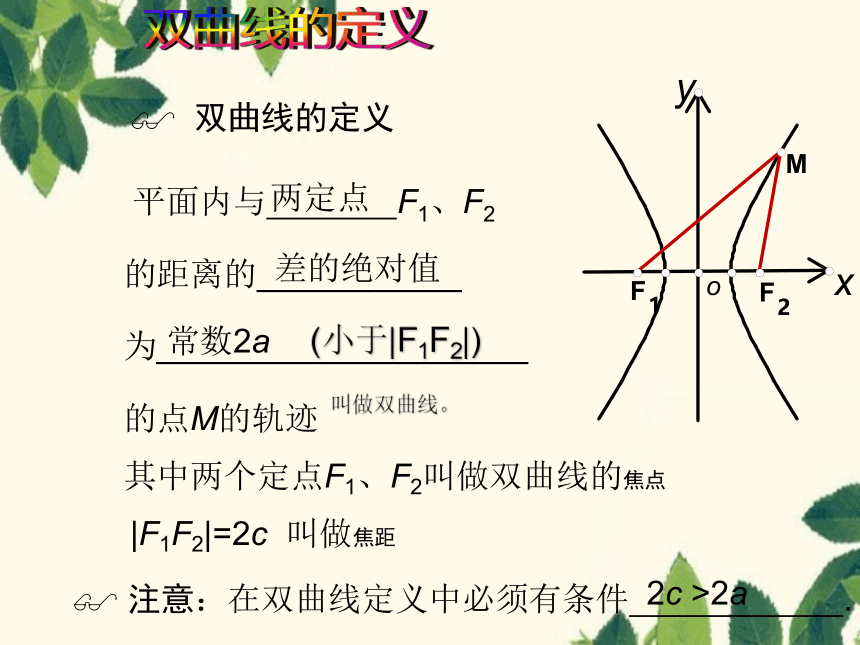
其中两个定点F1、F2叫做双曲线的焦点
|F1F2|=2c 叫做焦距
双曲线的定义
平面内与 F1、F2
的距离的___________ 为____________________
的点M的轨迹
两定点
差的绝对值
常数2a
注意:在双曲线定义中必须有条件 .
2c >2a
叫做双曲线。
双曲线的定义
(小于|F1F2|)
4)当0<a<c时,动点M的轨迹是什么?
动点M的轨迹是分别以点F1、F2为端点,
方向指向F1F2外侧的两条射线.
动点M的轨迹不存在.
2)当a>c>0时,动点M的轨迹是什么?
1)当a=c时,动点M的轨迹是什么?
3)若常数a=0,轨迹是什么
线段F1F2的垂直平分线
双曲线
小组讨论
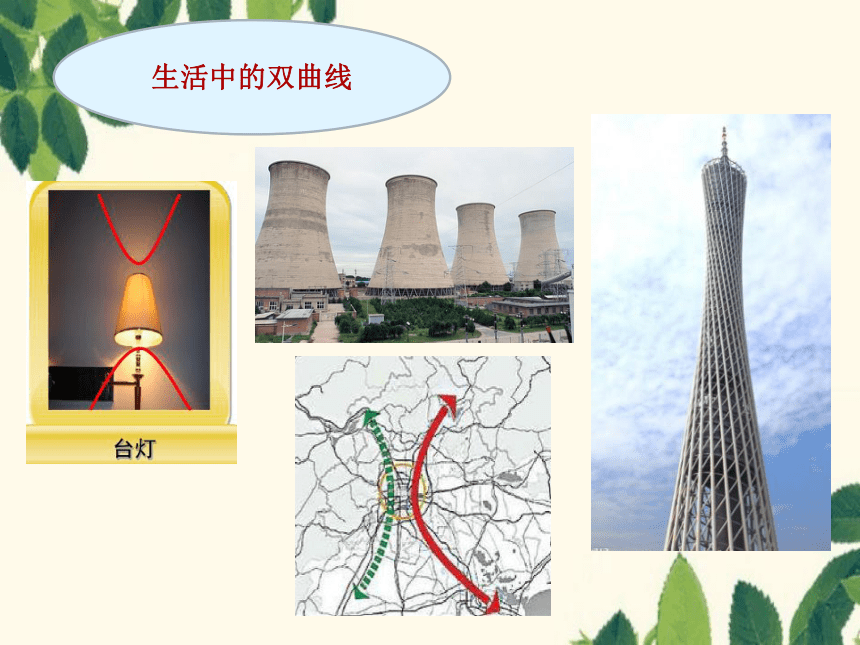
生活中的双曲线
小组合作推导 方程
洋葱视频播放双曲线方程推导过程
焦点在y轴上的双曲线的标准方程是:
想一想
方程的推导
双曲线和椭圆方程的异同点?
定义 图象
方程
焦点
a.b.c 的关系 | |MF1|-|MF2| | =2a(2a<|F1F2|)
F ( ±c, 0) F(0, ± ±c c)
双曲线两个方程的异同点
(椭圆 、 双曲线对比表)
椭圆 双曲线 定 义 图 形
方 程
焦点坐标
方程与定义的联系 焦点与方程的联系 a,b,c的关系 问题:如何判断焦点在哪个轴上?
F ( ±c, 0)
F(0, ± c)
基本运用
确定焦 点 位置:
椭圆看分母大小
双曲看系数正负
游戏pk
知识应用 巩固提升
例1, 已知双曲线的焦点为F1(-5,0),F2(5,0),双曲线上一点P到F1、F2的距离的差的绝对值等于6,求双曲线的标准方程.
变式(1) 已知双曲线的焦点为F1(0,-5)( 0,5) 双曲线上一点P到F1、F2的距离的差的绝对值等于6,求双曲线的标准方程.
变式(2)已知双曲线的焦点为F1(-5,0),F2(5,0),双曲线上一点P到F1、F2的距离的差等于6,求双曲线的标准方程.
归纳总结 知识升华
课后作业
1、必做题
2、选做题
3、利用猿题库app刷题自我提升
①焦点为(0,-6)(0,6),经过点(2,-5)
②a= 经过点A(-5,2),焦点在x轴上。
板书设计
椭圆及其标准方程
新课引入 合理建系,推导方程
归纳定义 应用举例
巩固练习
课堂小结
课外作业
学生在本节课中是学习的主体,学生自主探究主动学习。教师在本节课中是组织者、管理者,适时引导学生通过问题链进行自我建构、自我发展相关知识。本课中的媒体起到创设情境的作用。传统的教学采用教师讲授、证明结论、应用解题等教学方式。而我的课堂利用微视频引入,导课自然、生动、快速有效、形象直观。不但激发学生们的学习兴趣,还能培养学生们的数学抽象和数学建模能力。几何画板在本节课中应用特别大,它为我们提供强有力的技术支撑。将数学抽象的知识直观地呈现出来,充分的发挥了学生的自主探究能力,最大程度的调动了学生们课堂参与积极性。
互动练习环节,利用班级优化大师将全班同学的姓名放在光荣榜上,随机抽取一名同学回答问题,可以避免学生溜号,学生时刻处于紧张的学习状态,对于课堂上积极回答问题的同学给予多维度的不同方面的及时点评,,及时的肯定和点评,相应分数在光荣榜上排序,充分调动学生们的竞争意识。同时家长也可以利用班级优化大师app及时了解孩子们在课堂上的表现。
以学定教,培养了学生终身学习的能力,提升了数学核心素养。雨课堂、班级优化大师与翻转课堂的完美结合,做到学生课前自学,课上师生积极互动,课后巩固提升,从而打造高效课堂。
教学评价
双曲线的标准方程
1. 什么叫做椭圆?
两定点F1、F2
(|F1F2|=2c)
和
的距离的
等于常数
2a
( 2a>|F1F2|=2c>0)
的点的轨迹.
平面内与
引入问题:
两定点F1、F2
差
的距离的
等于常数
的点的轨迹 是什么呢?
平面内与
问题引入
动画
动画
小组合作作图
演示实验
几何画板动画演示
分别说出这两条曲线上点满足的条件?
双曲线的定义
M点运动时,M点满足什么条件?
∵|MF1|=|MF|=|MF2|+|F2F|
①如图(A),当 |MF1|>|MF2| 时
∴ |MF1|-|MF2|=|F2F|=2a
②如图(B),当 |MF1|<|MF2| 时
同理可得: |MF2|-|MF1|=2a
上面 两条合起来叫做双曲线
由①②可得:
| |MF1|-|MF2| | = 2a
(差的绝对值)
其中两个定点F1、F2叫做双曲线的焦点
|F1F2|=2c 叫做焦距
双曲线的定义
平面内与 F1、F2
的距离的___________ 为____________________
的点M的轨迹
两定点
差的绝对值
常数2a
注意:在双曲线定义中必须有条件 .
2c >2a
叫做双曲线。
双曲线的定义
(小于|F1F2|)
4)当0<a<c时,动点M的轨迹是什么?
动点M的轨迹是分别以点F1、F2为端点,
方向指向F1F2外侧的两条射线.
动点M的轨迹不存在.
2)当a>c>0时,动点M的轨迹是什么?
1)当a=c时,动点M的轨迹是什么?
3)若常数a=0,轨迹是什么
线段F1F2的垂直平分线
双曲线
小组讨论
生活中的双曲线
小组合作推导 方程
洋葱视频播放双曲线方程推导过程
焦点在y轴上的双曲线的标准方程是:
想一想
方程的推导
双曲线和椭圆方程的异同点?
定义 图象
方程
焦点
a.b.c 的关系 | |MF1|-|MF2| | =2a(2a<|F1F2|)
F ( ±c, 0) F(0, ± ±c c)
双曲线两个方程的异同点
(椭圆 、 双曲线对比表)
椭圆 双曲线 定 义 图 形
方 程
焦点坐标
方程与定义的联系 焦点与方程的联系 a,b,c的关系 问题:如何判断焦点在哪个轴上?
F ( ±c, 0)
F(0, ± c)
基本运用
确定焦 点 位置:
椭圆看分母大小
双曲看系数正负
游戏pk
知识应用 巩固提升
例1, 已知双曲线的焦点为F1(-5,0),F2(5,0),双曲线上一点P到F1、F2的距离的差的绝对值等于6,求双曲线的标准方程.
变式(1) 已知双曲线的焦点为F1(0,-5)( 0,5) 双曲线上一点P到F1、F2的距离的差的绝对值等于6,求双曲线的标准方程.
变式(2)已知双曲线的焦点为F1(-5,0),F2(5,0),双曲线上一点P到F1、F2的距离的差等于6,求双曲线的标准方程.
归纳总结 知识升华
课后作业
1、必做题
2、选做题
3、利用猿题库app刷题自我提升
①焦点为(0,-6)(0,6),经过点(2,-5)
②a= 经过点A(-5,2),焦点在x轴上。
板书设计
椭圆及其标准方程
新课引入 合理建系,推导方程
归纳定义 应用举例
巩固练习
课堂小结
课外作业
学生在本节课中是学习的主体,学生自主探究主动学习。教师在本节课中是组织者、管理者,适时引导学生通过问题链进行自我建构、自我发展相关知识。本课中的媒体起到创设情境的作用。传统的教学采用教师讲授、证明结论、应用解题等教学方式。而我的课堂利用微视频引入,导课自然、生动、快速有效、形象直观。不但激发学生们的学习兴趣,还能培养学生们的数学抽象和数学建模能力。几何画板在本节课中应用特别大,它为我们提供强有力的技术支撑。将数学抽象的知识直观地呈现出来,充分的发挥了学生的自主探究能力,最大程度的调动了学生们课堂参与积极性。
互动练习环节,利用班级优化大师将全班同学的姓名放在光荣榜上,随机抽取一名同学回答问题,可以避免学生溜号,学生时刻处于紧张的学习状态,对于课堂上积极回答问题的同学给予多维度的不同方面的及时点评,,及时的肯定和点评,相应分数在光荣榜上排序,充分调动学生们的竞争意识。同时家长也可以利用班级优化大师app及时了解孩子们在课堂上的表现。
以学定教,培养了学生终身学习的能力,提升了数学核心素养。雨课堂、班级优化大师与翻转课堂的完美结合,做到学生课前自学,课上师生积极互动,课后巩固提升,从而打造高效课堂。
教学评价
