4.1.2指数函数的性质与图像 课件-2021-2022学年高一数学人教B版(2019)必修第二册(共23张PPT)
文档属性
| 名称 | 4.1.2指数函数的性质与图像 课件-2021-2022学年高一数学人教B版(2019)必修第二册(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
4.1.2 指数函数的图像与性质
实例1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个,4个分裂成8个…… ,那么1个这样的细胞经过x次分裂后,能得到y个细胞,试写出y与x的关系式?
“大千世界,无奇不有”从下面2个实例中,你能得出怎样的函数关系式?它们形式上有什么特点?你能得到什么结论?
问题1:大千世界
一、创设情境 引入新课
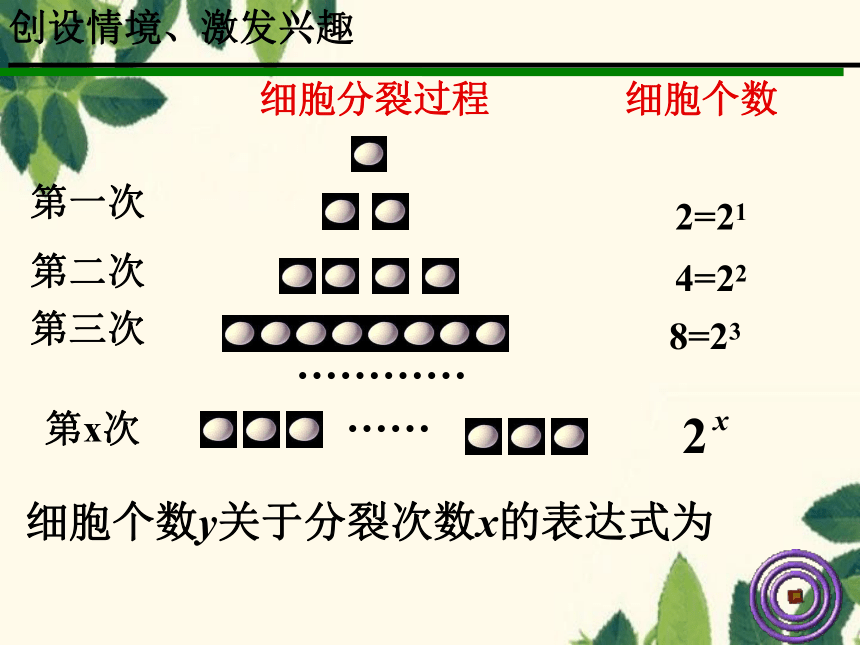
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
8=23
4=22
…………
第x次
……
细胞个数y关于分裂次数x的表达式为
创设情境、激发兴趣
一尺长的棍子,第一天截去其一半,第二天截去其剩余的一半,第三天截去第二天剩余部分的一半,依次截下去……,那么经过x天后,剩余棍子的长度y尺,试写出y和x之间的关系?
一、创设情境 引入新课
实例2:一尺之棰,日取其半 ,万世不竭。--庄子
(庄子)
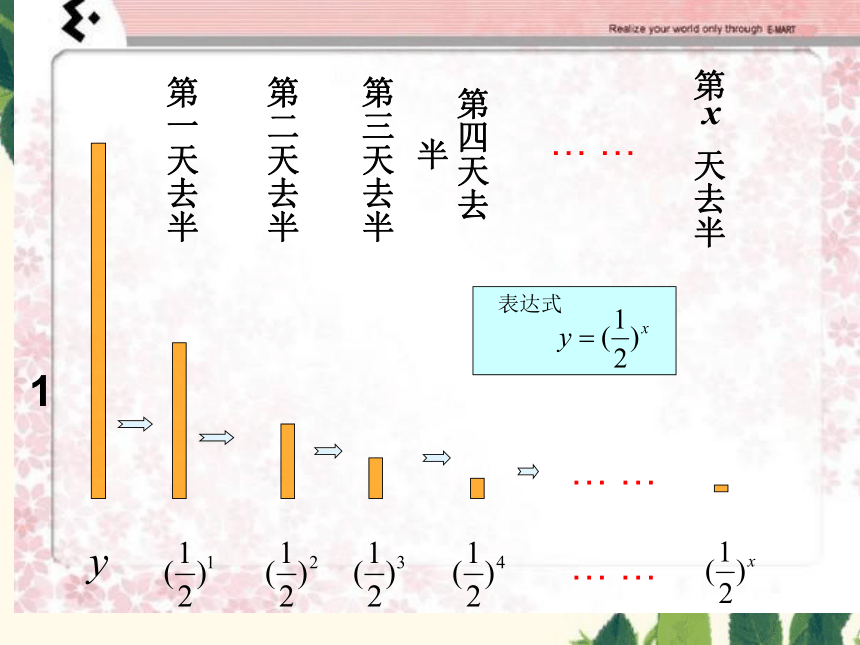
第一天去半
第二天去半
第三天去半
第四天去半
第 天去半
… …
1
表达式
… …
… …
前面我们从两个实例中抽象得到两个函数:
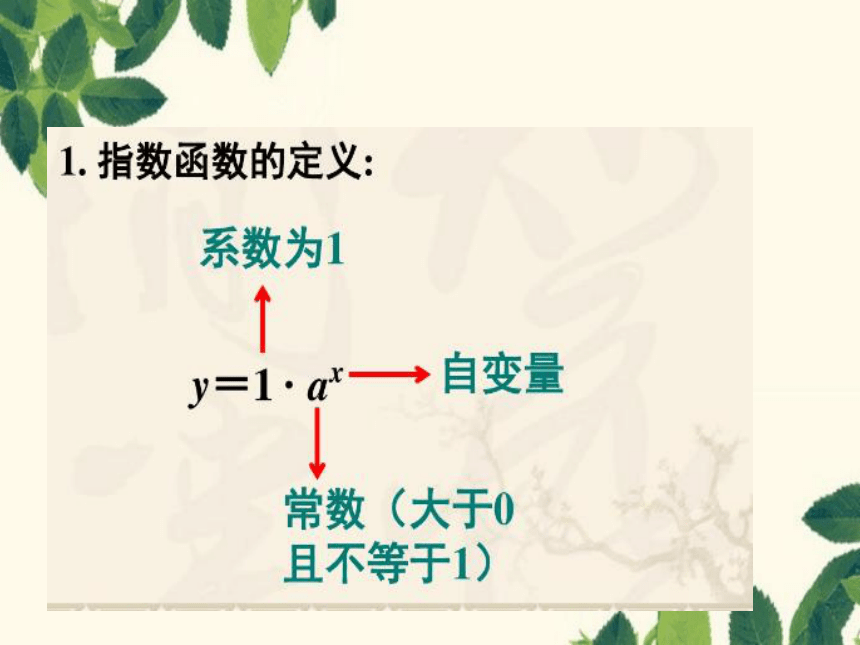
1、定义:
这两个函数表达式有何异同
函数y = ax(a 0,且a 1)叫做指数函数,其中x是自变量 .函数的定义域是R .
概念的形成
起个什么名字
注:回顾上一节的内容,我们发现指数 中p可以是有理数也可以是无理数,
所以指数函数的定义域是R。
p
a
探究:
概念深化、完善认识
0
1
a
设计意图:使学生对底数的取值范围,要知其然,
还要知其所以然;并从中体会分类讨论思想。
(1)如果 ,比如 ,这时对于 等,
在实数范围内函数值不存在;
(2)如果 , ;
(3)如果 , ,是常值函数,没有研究的必要;
(4)如果 或 ,即 ,当 是实数时,
都有意义.
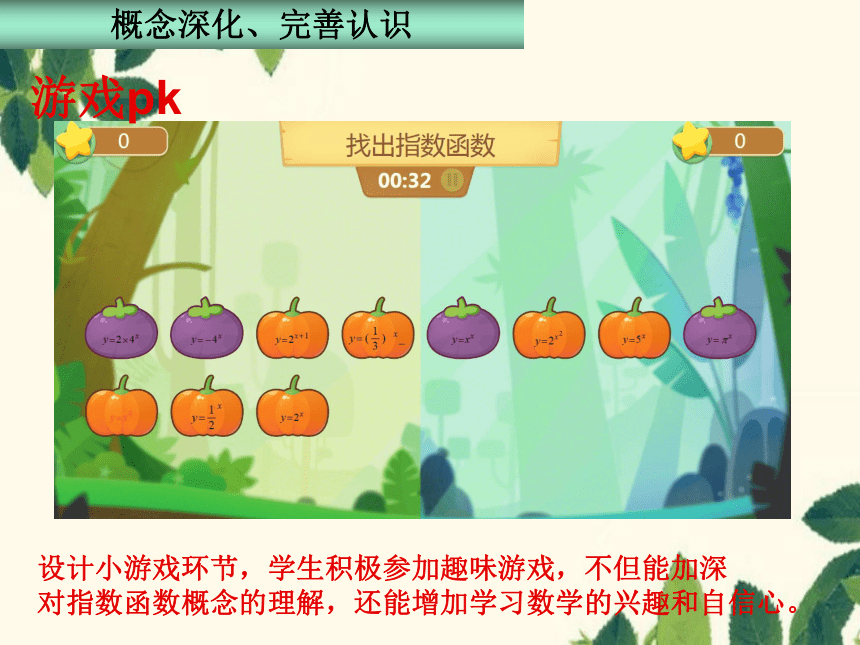
游戏pk
概念深化、完善认识
设计小游戏环节,学生积极参加趣味游戏,不但能加深
对指数函数概念的理解,还能增加学习数学的兴趣和自信心。
学生板演解题过程
(2)若函数
是指数函数,求
值。
(2)若函数
是指数函数,求
值。
合作互动、探求新知
学生活动:各小组成员合作,用描点法作函数图象。
教师活动:
教师活动:巡视并指导学生作图,然后用手机拍照利用希沃授课
助手的投屏功能投出学生的作品,再借助几何画板作图,动态演示
0
1
1
学生思考:1.底互为倒数的两指数函数图象间的关系?
2. 若把指数函数分类,该如何分?
0
1
1
0
1
1
0
1
0
1
设计意图:在学生自己画出四组指数函数图象的基础上,利用多媒体给
学生展示精确图象,引导学生发现底互为倒数的两指数函数图象间的对称关系,
并启发他们指数函数按底数可分为 两种类型。使其对图象印象深刻;
从而突出了本节课的第二个重点:指数函数图象。也突破了第一个难点:
指数函数图象的发现、总结过程。
几何画板模拟演示
在R上是减函数
在R上是增函数
单调性
(0,1)
(0,1)
过定点
x > 0时,0< y <1
x < 0时,y > 1
x > 0时,y > 1
x < 0时,0< y <1
函数值变化情况
R
R
值 域
(0,+∞)
(0,+∞)
定义域
图 象
函 数
(0,+∞)
(0,1)
性质
R
设计意图:分组讨论,给学生提供自主合作探究的机会,让学生充分参与到
课堂教学中。让学生体会用数形结合思想研究函数的性质。表格的完成将会使学生
体会到很大的成功感,增强学好数学的信心。
左右无限上冲天,
永与横轴不沾边.
大一增,小一减,
图象恒过(0,1)点.
教学过程
探
索
新
知
、
深
化
理
解
例题精析
例题精析
例题精析
课堂练习
利用指数函数的性质,比较下列各题中两个值的大小:
答案(1)大于 (2)小于 (3)大于
利用指数函数单调性比大小的方法 :
2.底数不同化成相同形式。
1.底数相同利用指数函数的单调性
教学过程
归
纳
总
结
、
知
识
升
华
设计意图:引导学生对指数函数的知识进行梳理,
利于学生系统掌握所学内容,深化知识与技能。
课后作业
1.必做题
2.选做题
3.猿题库app自我提升
4.1.2 指数函数的图像与性质
实例1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个,4个分裂成8个…… ,那么1个这样的细胞经过x次分裂后,能得到y个细胞,试写出y与x的关系式?
“大千世界,无奇不有”从下面2个实例中,你能得出怎样的函数关系式?它们形式上有什么特点?你能得到什么结论?
问题1:大千世界
一、创设情境 引入新课
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
8=23
4=22
…………
第x次
……
细胞个数y关于分裂次数x的表达式为
创设情境、激发兴趣
一尺长的棍子,第一天截去其一半,第二天截去其剩余的一半,第三天截去第二天剩余部分的一半,依次截下去……,那么经过x天后,剩余棍子的长度y尺,试写出y和x之间的关系?
一、创设情境 引入新课
实例2:一尺之棰,日取其半 ,万世不竭。--庄子
(庄子)
第一天去半
第二天去半
第三天去半
第四天去半
第 天去半
… …
1
表达式
… …
… …
前面我们从两个实例中抽象得到两个函数:
1、定义:
这两个函数表达式有何异同
函数y = ax(a 0,且a 1)叫做指数函数,其中x是自变量 .函数的定义域是R .
概念的形成
起个什么名字
注:回顾上一节的内容,我们发现指数 中p可以是有理数也可以是无理数,
所以指数函数的定义域是R。
p
a
探究:
概念深化、完善认识
0
1
a
设计意图:使学生对底数的取值范围,要知其然,
还要知其所以然;并从中体会分类讨论思想。
(1)如果 ,比如 ,这时对于 等,
在实数范围内函数值不存在;
(2)如果 , ;
(3)如果 , ,是常值函数,没有研究的必要;
(4)如果 或 ,即 ,当 是实数时,
都有意义.
游戏pk
概念深化、完善认识
设计小游戏环节,学生积极参加趣味游戏,不但能加深
对指数函数概念的理解,还能增加学习数学的兴趣和自信心。
学生板演解题过程
(2)若函数
是指数函数,求
值。
(2)若函数
是指数函数,求
值。
合作互动、探求新知
学生活动:各小组成员合作,用描点法作函数图象。
教师活动:
教师活动:巡视并指导学生作图,然后用手机拍照利用希沃授课
助手的投屏功能投出学生的作品,再借助几何画板作图,动态演示
0
1
1
学生思考:1.底互为倒数的两指数函数图象间的关系?
2. 若把指数函数分类,该如何分?
0
1
1
0
1
1
0
1
0
1
设计意图:在学生自己画出四组指数函数图象的基础上,利用多媒体给
学生展示精确图象,引导学生发现底互为倒数的两指数函数图象间的对称关系,
并启发他们指数函数按底数可分为 两种类型。使其对图象印象深刻;
从而突出了本节课的第二个重点:指数函数图象。也突破了第一个难点:
指数函数图象的发现、总结过程。
几何画板模拟演示
在R上是减函数
在R上是增函数
单调性
(0,1)
(0,1)
过定点
x > 0时,0< y <1
x < 0时,y > 1
x > 0时,y > 1
x < 0时,0< y <1
函数值变化情况
R
R
值 域
(0,+∞)
(0,+∞)
定义域
图 象
函 数
(0,+∞)
(0,1)
性质
R
设计意图:分组讨论,给学生提供自主合作探究的机会,让学生充分参与到
课堂教学中。让学生体会用数形结合思想研究函数的性质。表格的完成将会使学生
体会到很大的成功感,增强学好数学的信心。
左右无限上冲天,
永与横轴不沾边.
大一增,小一减,
图象恒过(0,1)点.
教学过程
探
索
新
知
、
深
化
理
解
例题精析
例题精析
例题精析
课堂练习
利用指数函数的性质,比较下列各题中两个值的大小:
答案(1)大于 (2)小于 (3)大于
利用指数函数单调性比大小的方法 :
2.底数不同化成相同形式。
1.底数相同利用指数函数的单调性
教学过程
归
纳
总
结
、
知
识
升
华
设计意图:引导学生对指数函数的知识进行梳理,
利于学生系统掌握所学内容,深化知识与技能。
课后作业
1.必做题
2.选做题
3.猿题库app自我提升
