4.3.2等比数列前n项和公式 课件-2021-2022学年高二下学期数学 人教A版(2019)选择性必修第二册(共14张PPT)
文档属性
| 名称 | 4.3.2等比数列前n项和公式 课件-2021-2022学年高二下学期数学 人教A版(2019)选择性必修第二册(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 473.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 09:21:22 | ||
图片预览






文档简介
(共14张PPT)
§ 4.3 等比数列的前n项和公式
陛下,请您在这张棋盘的第一个小格内,赏给我一粒麦子;在第二个小格内给两粒,第三格内给四粒,照这样下去,每一小格里放的麦粒数都是前一小格的二倍,直到第64格的麦粒,都赏给您的仆人罢!
数学小故事
第1格:
第2格:
第4格:
第3格:
第63格:
第64格:
1
2
……
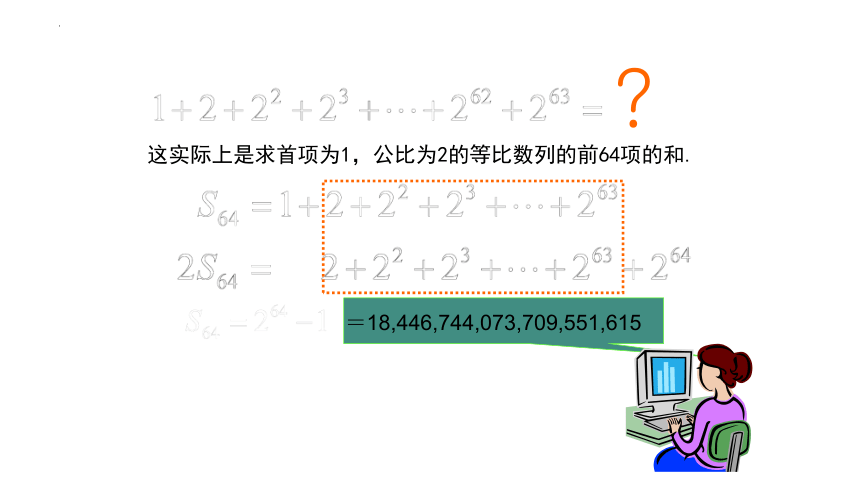
这实际上是求首项为1,公比为2的等比数列的前64项的和.
=18,446,744,073,709,551,615
对于一般的等比数列我们又将怎样求得它的前n项和呢
两边同时乘以 为
设 为等比数列, 为首项, 为公比,它的前n项和
①
错位相减
由① 得
②
分类讨论
当 时,
当 时,
?
即 是一个常数列
等比数列的通项公式
错位相减法
,q=
=1-
=
练习1.设等比数列{an}的前n项和为Sn,a1=3,公比q=2,则a4= ,S3= .
24
21
例2.在等比数列{an}中,公比为q,前n项和为Sn.若a1=1,a5=16,且q>0,求S7;
解:(1)∵{an}为等比数列且a1=1,a5=16,
∴a5=a1q4,即16=q4,
∴a5=a1q4,即16=q4,
解得q=2(负值舍去),
∴S7===127.
练习2.设等比数列{an}的前n项和是Sn,a2=-2,a5=-16,则S6=( )
A.-63 B.63
C.-31 D.31
[解析]设等比数列{an}的公比为q,
则a5=a2q3,
即-16=-2q3,
解得q=2,
所以a1==-1,
所以S6===-63.
A
例3.已知等比数列{an}的前n项和为Sn,若a1+a3=3,a2+a4=6,则S8=( )
A.45 B.81
C.117 D.153
D
练习3.若a2=6,6a1+a3=30,则an= ,
Sn= .
3
3
方程思想
整体思想
,q=2
q=-
练习4.已知等比数列{an}的公比为q,其前n项和为Sn,若S4=1,S8=17,则an= .
×2n-1或-×(-2)n-1
[解析] 若q=1,则S8=2S4,不合题意,∴q≠1,
∴S4==1,
S8==17,
两式相除得=17=1+q4,
解得q=2或q=-2,
∴a1=或a1=-,
∴an=×2n-1或an=-×(-2)n-1.
B
B
,q=-2
§ 4.3 等比数列的前n项和公式
陛下,请您在这张棋盘的第一个小格内,赏给我一粒麦子;在第二个小格内给两粒,第三格内给四粒,照这样下去,每一小格里放的麦粒数都是前一小格的二倍,直到第64格的麦粒,都赏给您的仆人罢!
数学小故事
第1格:
第2格:
第4格:
第3格:
第63格:
第64格:
1
2
……
这实际上是求首项为1,公比为2的等比数列的前64项的和.
=18,446,744,073,709,551,615
对于一般的等比数列我们又将怎样求得它的前n项和呢
两边同时乘以 为
设 为等比数列, 为首项, 为公比,它的前n项和
①
错位相减
由① 得
②
分类讨论
当 时,
当 时,
?
即 是一个常数列
等比数列的通项公式
错位相减法
,q=
=1-
=
练习1.设等比数列{an}的前n项和为Sn,a1=3,公比q=2,则a4= ,S3= .
24
21
例2.在等比数列{an}中,公比为q,前n项和为Sn.若a1=1,a5=16,且q>0,求S7;
解:(1)∵{an}为等比数列且a1=1,a5=16,
∴a5=a1q4,即16=q4,
∴a5=a1q4,即16=q4,
解得q=2(负值舍去),
∴S7===127.
练习2.设等比数列{an}的前n项和是Sn,a2=-2,a5=-16,则S6=( )
A.-63 B.63
C.-31 D.31
[解析]设等比数列{an}的公比为q,
则a5=a2q3,
即-16=-2q3,
解得q=2,
所以a1==-1,
所以S6===-63.
A
例3.已知等比数列{an}的前n项和为Sn,若a1+a3=3,a2+a4=6,则S8=( )
A.45 B.81
C.117 D.153
D
练习3.若a2=6,6a1+a3=30,则an= ,
Sn= .
3
3
方程思想
整体思想
,q=2
q=-
练习4.已知等比数列{an}的公比为q,其前n项和为Sn,若S4=1,S8=17,则an= .
×2n-1或-×(-2)n-1
[解析] 若q=1,则S8=2S4,不合题意,∴q≠1,
∴S4==1,
S8==17,
两式相除得=17=1+q4,
解得q=2或q=-2,
∴a1=或a1=-,
∴an=×2n-1或an=-×(-2)n-1.
B
B
,q=-2
