5.3.1等比数列 课件-2021-2022学年高二数学人教B版(2019)选择性必修第三册(共22张PPT)
文档属性
| 名称 | 5.3.1等比数列 课件-2021-2022学年高二数学人教B版(2019)选择性必修第三册(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 09:20:45 | ||
图片预览






文档简介
(共22张PPT)
5.3.1 等比数列第1课时 等比数列的定义(一)复习旧知
如果一碗面由256根面条组成,请问需要拉面师傅拉几次才能得到
(二)创设情境 形成概念
舌尖中国
我国古代一些学者提出:“一尺之棰,日取其半,万世不竭。”即一尺长的木棒,每日取其一半,永远也取不完,这样每天剩下的部分都是前一天的一半。如果把“一尺之棰”看成单位“1”,那么得到的数列是
某种汽车购买时的价格是10万元,每年的折旧率是15%,这辆车各年开始时的价值(单位:万元)分别是:
10,10×0.85,10×0.852 ,10×0.853,…
拉面时前9次拉伸成的面条根数构成一个数列:
上面数列有什么共同特点
从第二项起,每一项与前一项的比都等于同一个常数。
1, 2, 4, 8, 16, 32, 64, 128, 256
10,10×0.85,10×0.852 ,10×0.853,…
1, 2, 4, 8, 16, 32, 64, 128, 256
(三) 合作互动 探求新知
由以上数列的共同特点,形成等比数列定义:
如果一个数列从第二项起,每一项与它
的前一项的比等于同一个常数,那么这个数
列就叫做等比数列.这个常数叫做等比数列的
公比,公比通常用字母 表示.
回顾:以上四个数列共同特点的引导过程
思考:数学语
言如何描述?
或
其数学表达式
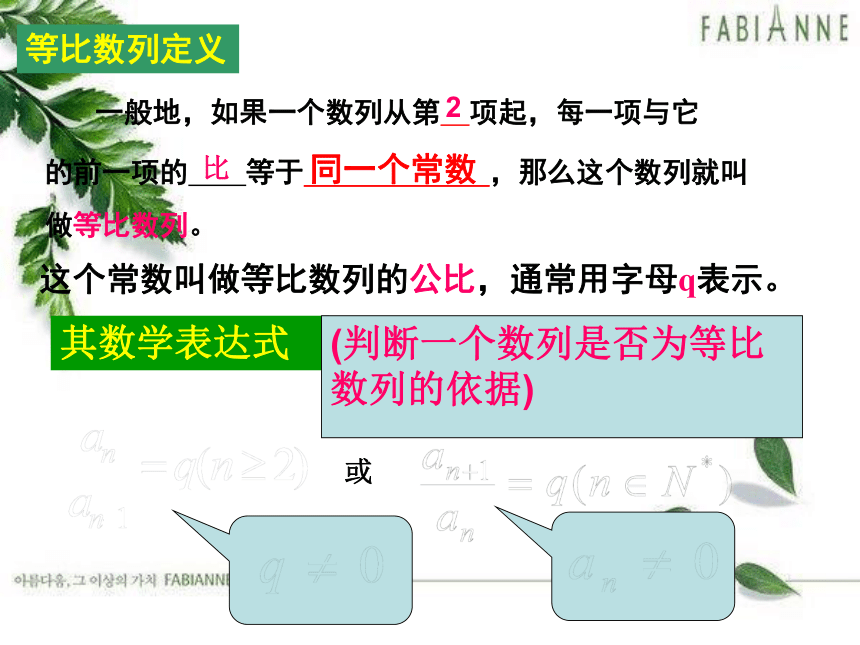
等比数列定义
一般地,如果一个数列从第 项起,每一项与它
的前一项的 等于 ,那么这个数列就叫
做等比数列。
这个常数叫做等比数列的公比,通常用字母q表示。
比
同一个常数
2
(判断一个数列是否为等比数列的依据)
如果
那么数列
是否为等比数列?
思考
教师提问
学生小组讨论
归纳
等比数列定义的限定条件:
学生对完整的定义有了初步的认识
pk游戏找出等比数列
等比中项
问题4: 你能通过类比等差中项猜想等比中项吗?
回顾类比 等差中项:
猜想 等比中项:
证明 等比中项:根据等比数列定义.
等比中项定义:如果在 与 中间插入一个数 ,使 成等比数列,那么 叫做 与 的等比中项.
再次强调
类比思想
巩固练习
等比数列通项公式的推导
回忆
等差数列通项公式:
类比
已知首项和公比,怎样写出通项公式?
猜想
推导
证明
和→积→乘方 (运算升级)
.
等比数列的通项公式:
不完全归纳法
叠乘法
熟悉叠乘法,
化解教学难点
回顾等差数列
小组完成推导
Ⅰ 通项公式
不完全归纳法
通项公式的推导
当 时,上述式子仍然成立.
因而,对于等比数列的第一项必须补充说明,从而得出通项公式
提问:这种方法是否严密?
通项公式的证明
叠乘法
将以上 个式子相乘,
当 时,上式仍然成立.
得出通项公式
思考:还有其它证明方法吗?
问题1 等比数列通项公式是否有更一般的形式?
Ⅱ 通项公式推广
类比 等差数列通项公式的推广:
猜想 等比数列通项公式的推广:
证明 等比数列通项公式的推广:
问题2 怎么证明
问题2留给学生作为课后作业.可提示学生,
运用通项公式及方程思想来进行证明即可得出.
Ⅲ 通项公式的图象
问题3 如何画通项公式
与
的图象?
你能观察出它们的图象特征吗,请给出说明.
过程:
1.学生动手画图象;
2.教师利用几何画板作出数列图象;
3.学生观察图象,探究通项公式与函数的关系.
函数观点:等比数列是一类特殊的函数,
是建立在定义域为正整数集上的函数.
(五) 知识运用 巩固提高
例1 若一个等比数列的第3项和第4项分
别是12和18,求它的第1项和第2项.
例2 在等比数列
中,
一题多解
(六) 练习巩固
2、 已知一个等比数列的第2项是10,
第3项是20,求它的第1项与第4项.
1、 已知一个等比数列的第5项是
公比是
求它的第1项.
学生动手做题,在例题基础上进一步巩固所学.
学生独立完成为主,教师个别指导为辅.
考查内容:等比数列的通项公式
本题采用等比中项解题是最迅速最简便的方法.
设计意图:增强对通项公式及其推广、变形和等比中项的理解与运用,提高解决问题的能力.
归纳解题的思想方法:
(1)运用方程知三求一的思想(已知方程四个量
中的任三个,可求出第四个量).
(2)先化简变形,后代值计算.
而
(3)若已知
未知,则可以直接运用
通项公式的推广公式解题.
(4)若已知等比数列的第m-1项和第m+1项,要求
第m项,可以由等比中项立即得出.
归纳总结 知识升华
布置作业 分层练习
1.必做题
2.选做题
3.用猿题库APP课后巩固提升
板书设计
等比数列
一、问题
二、等比数列
1.定义
2.通项公式
(1)推导
(2)公式
(3)推广公式
3.图象(函数观点)
4.等比中项
三、例题应用
1.方程思想
2.公式运用
四、练习巩固
五、课堂小结
1.重点内容
2.思想方法
六、作业布置
浓缩教学内容,突出重难点,
形成知识脉络
5.3.1 等比数列第1课时 等比数列的定义(一)复习旧知
如果一碗面由256根面条组成,请问需要拉面师傅拉几次才能得到
(二)创设情境 形成概念
舌尖中国
我国古代一些学者提出:“一尺之棰,日取其半,万世不竭。”即一尺长的木棒,每日取其一半,永远也取不完,这样每天剩下的部分都是前一天的一半。如果把“一尺之棰”看成单位“1”,那么得到的数列是
某种汽车购买时的价格是10万元,每年的折旧率是15%,这辆车各年开始时的价值(单位:万元)分别是:
10,10×0.85,10×0.852 ,10×0.853,…
拉面时前9次拉伸成的面条根数构成一个数列:
上面数列有什么共同特点
从第二项起,每一项与前一项的比都等于同一个常数。
1, 2, 4, 8, 16, 32, 64, 128, 256
10,10×0.85,10×0.852 ,10×0.853,…
1, 2, 4, 8, 16, 32, 64, 128, 256
(三) 合作互动 探求新知
由以上数列的共同特点,形成等比数列定义:
如果一个数列从第二项起,每一项与它
的前一项的比等于同一个常数,那么这个数
列就叫做等比数列.这个常数叫做等比数列的
公比,公比通常用字母 表示.
回顾:以上四个数列共同特点的引导过程
思考:数学语
言如何描述?
或
其数学表达式
等比数列定义
一般地,如果一个数列从第 项起,每一项与它
的前一项的 等于 ,那么这个数列就叫
做等比数列。
这个常数叫做等比数列的公比,通常用字母q表示。
比
同一个常数
2
(判断一个数列是否为等比数列的依据)
如果
那么数列
是否为等比数列?
思考
教师提问
学生小组讨论
归纳
等比数列定义的限定条件:
学生对完整的定义有了初步的认识
pk游戏找出等比数列
等比中项
问题4: 你能通过类比等差中项猜想等比中项吗?
回顾类比 等差中项:
猜想 等比中项:
证明 等比中项:根据等比数列定义.
等比中项定义:如果在 与 中间插入一个数 ,使 成等比数列,那么 叫做 与 的等比中项.
再次强调
类比思想
巩固练习
等比数列通项公式的推导
回忆
等差数列通项公式:
类比
已知首项和公比,怎样写出通项公式?
猜想
推导
证明
和→积→乘方 (运算升级)
.
等比数列的通项公式:
不完全归纳法
叠乘法
熟悉叠乘法,
化解教学难点
回顾等差数列
小组完成推导
Ⅰ 通项公式
不完全归纳法
通项公式的推导
当 时,上述式子仍然成立.
因而,对于等比数列的第一项必须补充说明,从而得出通项公式
提问:这种方法是否严密?
通项公式的证明
叠乘法
将以上 个式子相乘,
当 时,上式仍然成立.
得出通项公式
思考:还有其它证明方法吗?
问题1 等比数列通项公式是否有更一般的形式?
Ⅱ 通项公式推广
类比 等差数列通项公式的推广:
猜想 等比数列通项公式的推广:
证明 等比数列通项公式的推广:
问题2 怎么证明
问题2留给学生作为课后作业.可提示学生,
运用通项公式及方程思想来进行证明即可得出.
Ⅲ 通项公式的图象
问题3 如何画通项公式
与
的图象?
你能观察出它们的图象特征吗,请给出说明.
过程:
1.学生动手画图象;
2.教师利用几何画板作出数列图象;
3.学生观察图象,探究通项公式与函数的关系.
函数观点:等比数列是一类特殊的函数,
是建立在定义域为正整数集上的函数.
(五) 知识运用 巩固提高
例1 若一个等比数列的第3项和第4项分
别是12和18,求它的第1项和第2项.
例2 在等比数列
中,
一题多解
(六) 练习巩固
2、 已知一个等比数列的第2项是10,
第3项是20,求它的第1项与第4项.
1、 已知一个等比数列的第5项是
公比是
求它的第1项.
学生动手做题,在例题基础上进一步巩固所学.
学生独立完成为主,教师个别指导为辅.
考查内容:等比数列的通项公式
本题采用等比中项解题是最迅速最简便的方法.
设计意图:增强对通项公式及其推广、变形和等比中项的理解与运用,提高解决问题的能力.
归纳解题的思想方法:
(1)运用方程知三求一的思想(已知方程四个量
中的任三个,可求出第四个量).
(2)先化简变形,后代值计算.
而
(3)若已知
未知,则可以直接运用
通项公式的推广公式解题.
(4)若已知等比数列的第m-1项和第m+1项,要求
第m项,可以由等比中项立即得出.
归纳总结 知识升华
布置作业 分层练习
1.必做题
2.选做题
3.用猿题库APP课后巩固提升
板书设计
等比数列
一、问题
二、等比数列
1.定义
2.通项公式
(1)推导
(2)公式
(3)推广公式
3.图象(函数观点)
4.等比中项
三、例题应用
1.方程思想
2.公式运用
四、练习巩固
五、课堂小结
1.重点内容
2.思想方法
六、作业布置
浓缩教学内容,突出重难点,
形成知识脉络
