6.2.1-2排列与排列数公式 课件-2021-2022学年高二下学期数学 人教A版(2019)选择性必修第三册(共22张PPT)
文档属性
| 名称 | 6.2.1-2排列与排列数公式 课件-2021-2022学年高二下学期数学 人教A版(2019)选择性必修第三册(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 912.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 09:27:57 | ||
图片预览





文档简介
(共22张PPT)
6.2.1-2排列与
排列数公式
1.分类加法计数原理:
完成一件事,有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法 …在第n类方案中有mn种不同的方法.那么完成这
件事共有 种不同的方法.
2.分步乘法计数原理:
完成一件事,需要分成n个步骤,做 第 1 步有
m1种不同的方法,做第2步有m2种不同的方法…,
做 第 n 步 有mn种不同的方法.那 么 完 成这件 事
共有 种不同的方法.
回顾旧知
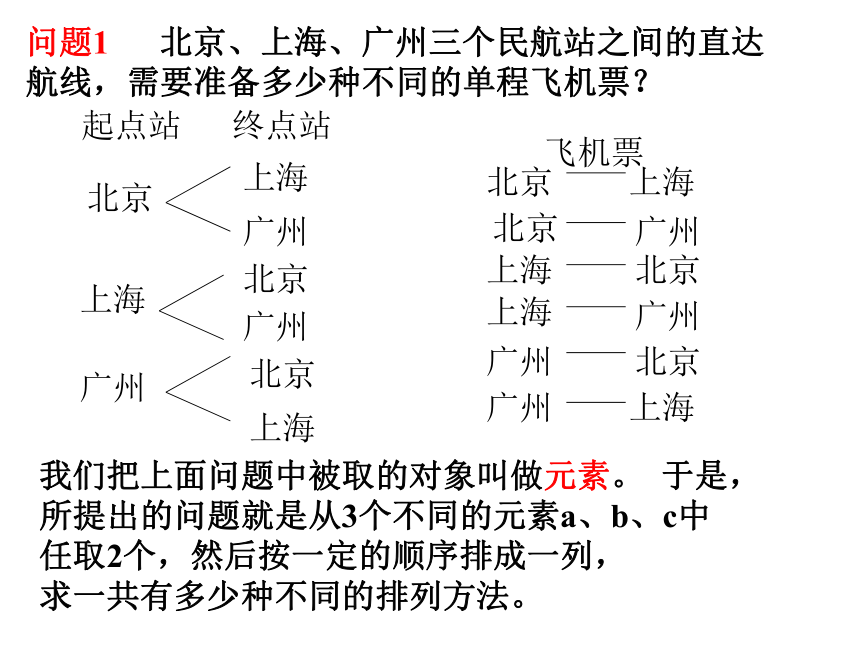
问题1 北京、上海、广州三个民航站之间的直达航线,需要准备多少种不同的单程飞机票?
起点站 终点站
北京
上海
北京
北京
上海
上海
广州
广州
广州
飞机票
北京
北京
北京
北京
上海
广州
上海
上海
上海
广州
广州
广州
我们把上面问题中被取的对象叫做元素。 于是,所提出的问题就是从3个不同的元素a、b、c中任取2个,然后按一定的顺序排成一列,
求一共有多少种不同的排列方法。
1
2
3
4
1
2
1
3
1
4
1
2
3
1
2
4
1
3
2
1
3
4
1
4
2
1
4
3
3
4
3
2
3
1
3
1
2
3
1
4
3
4
2
3
2
1
3
2
4
3
4
1
2
1
2
3
2
4
2
1
3
2
1
4
2
3
1
2
3
4
2
4
1
2
4
3
4
1
4
2
4
3
4
1
2
4
1
3
4
2
1
4
2
3
4
3
1
4
3
2
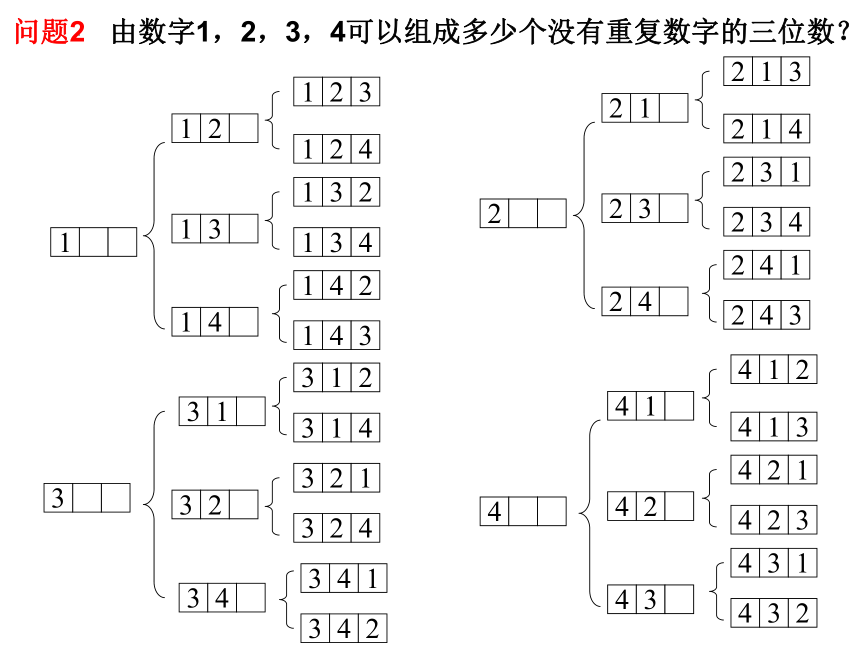
问题2 由数字1,2,3,4可以组成多少个没有重复数字的三位数?
问题3:问题1、问题2 的共同特点是?能否推广到一般?
问题1和问题2都是研究从一些不同元素中取出部分元素,并按照一定的顺序排成一列的方法数.
(一)排列:一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
问题2:从4个不同的元素a,b,c,d中任取3个,然后按照一定的顺序排成一列.
问题1:从3个不同的元素a,b,c中任意取出2个,并按一定的顺序排成一列.
基本概念
说明:
1、元素不能重复。n个中不能重复,m个中也不能重复.
2、“按一定顺序”就是与位置有关,这是判断一个问题是否是排列问题的关键。
3、两个排列相同,当且仅当这两个排列中的元素完全相同,而且元素的排列顺序也完全相同。
4、m<n时的排列叫选排列,m=n时的排列叫全排列。
5、为了使写出的所有排列情况既不重复也不遗漏,最好采用“树形图”。
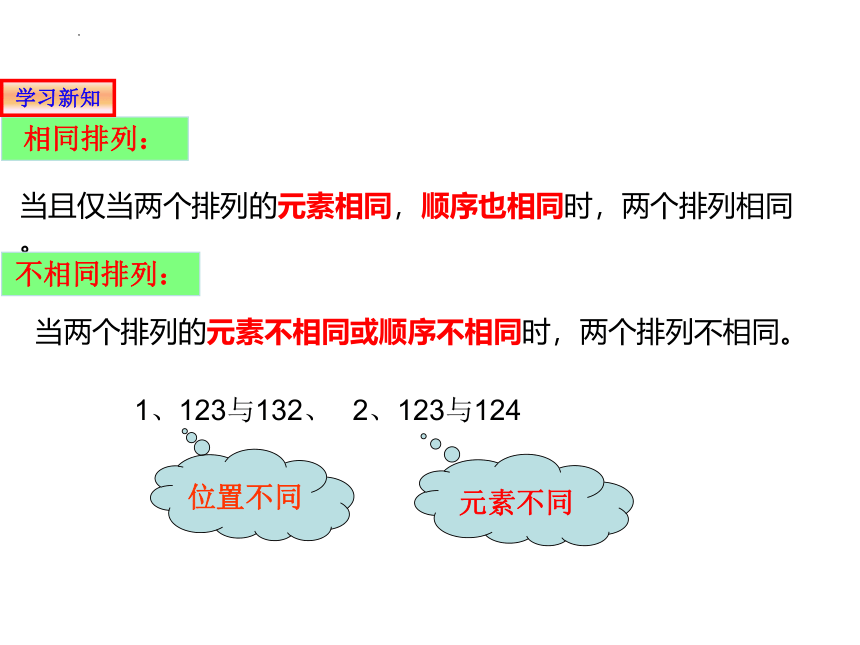
相同排列:
当且仅当两个排列的元素相同,顺序也相同时,两个排列相同。
不相同排列:
当两个排列的元素不相同或顺序不相同时,两个排列不相同。
1、123与132、
2、123与124
位置不同
元素不同
学习新知
例1、下列问题中哪些是排列问题?
(1)10名学生中抽2名学生开会
(2)10名学生中选2名做正、副组长
(3)从2,3,5,7,11中任取两个数相乘
(4)从2,3,5,7,11中任取两个数相除
(5)20位同学互通一次电话
(6)有10个车站,共需要多少种车票?
(7)有10个车站,共需要多少种不同的票价?
不是
是
不是
不是
不是
是
是
例题讲评
(8)从高二17班全体同学中选5人组成课外数学学习小组;
(9)从高二18班全体同学中选5人分别参加校运动会的5个不同运动项目;
不是
是
(1)首先要保证元素无重复性,即从n个不同元素中,取出m(m≤n)个不同的元素,否则不是排列问题。
(2)要保证元素的有序性,即安排这m个元素时是有序的,有序就是排列,无序则不是排列.
而检验它是否有序的依据就是变换元素的位置,看结果是否发生变化,有变化是有序,无变化就是无序.
排列问题的判断方法:
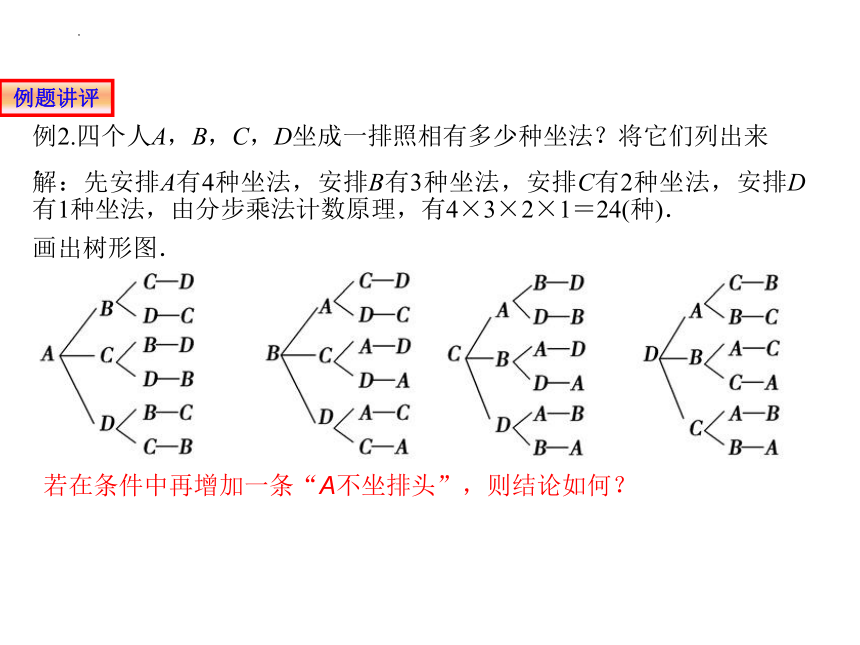
例2.四个人A,B,C,D坐成一排照相有多少种坐法?将它们列出来.
解:先安排A有4种坐法,安排B有3种坐法,安排C有2种坐法,安排D有1种坐法,由分步乘法计数原理,有4×3×2×1=24(种).
画出树形图.
若在条件中再增加一条“A不坐排头”,则结论如何?
例题讲评
(二).排列数:
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m个元素的排列数。用符号 表示。
“排列”和“排列数”有什么区别和联系?
“一个排列”是指:从n个不同元素中,任取m个元素按照一定的顺序排成一列,不是数;
“排列数”是指:从n个不同元素中,任取m个元素所有排列的个数,是一个数;所以符号 只表示排列数,而不表示具体的排列.
基本概念
1)问题1:中是求从3个不同元素中取出2个元 素的排列数,记为 ,已经算得
2)问题2:中是求从4个不同元素中取出3个元素的排列数,记为 ,已经算出
3).从n个不同元素中取出2个元素的排列数是多少
呢?
呢?
……
第1位
第2位
第3位
第m位
n种
(n-1)种
(n-2)种
(n-m+1)种
探究:
(三)排列数公式(1):
当m=n时,
正整数1到n的连乘积,叫做n的阶乘,用 表示。
n个不同元素的全排列公式:
排列数公式(2):
说明:
①排列数公式的第一个常用来计算,第二个常用来证明.
为了使当m=n时上面的公式也成立,规定:
②.对于 这个条件要留意,往往是解方程时的隐含条件.
!
n
例3. 计算:
(1)
(2)
(3 )
解:(1)
(3)
(2)
(4)
(4)
例4.证明:
证明:右边
变式练习:
由n=18,n-m+1=8,得m=11
18
11
8
15
几种特殊的排列
1.优先排列
2.集团排列(捆绑法)
3.间隔排列
4.有序排列
综合练习
四.课堂小结:
1.排列:从n个不同元素中选出m(m≤n)个元素,并按
一定的顺序排成一列.
2.关键点:1.互异性(被选、所选元素互不相同)
2.有序性(所选元素有先后位置等顺序之分)
3.排列数:所有排列总数
6.2.1-2排列与
排列数公式
1.分类加法计数原理:
完成一件事,有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法 …在第n类方案中有mn种不同的方法.那么完成这
件事共有 种不同的方法.
2.分步乘法计数原理:
完成一件事,需要分成n个步骤,做 第 1 步有
m1种不同的方法,做第2步有m2种不同的方法…,
做 第 n 步 有mn种不同的方法.那 么 完 成这件 事
共有 种不同的方法.
回顾旧知
问题1 北京、上海、广州三个民航站之间的直达航线,需要准备多少种不同的单程飞机票?
起点站 终点站
北京
上海
北京
北京
上海
上海
广州
广州
广州
飞机票
北京
北京
北京
北京
上海
广州
上海
上海
上海
广州
广州
广州
我们把上面问题中被取的对象叫做元素。 于是,所提出的问题就是从3个不同的元素a、b、c中任取2个,然后按一定的顺序排成一列,
求一共有多少种不同的排列方法。
1
2
3
4
1
2
1
3
1
4
1
2
3
1
2
4
1
3
2
1
3
4
1
4
2
1
4
3
3
4
3
2
3
1
3
1
2
3
1
4
3
4
2
3
2
1
3
2
4
3
4
1
2
1
2
3
2
4
2
1
3
2
1
4
2
3
1
2
3
4
2
4
1
2
4
3
4
1
4
2
4
3
4
1
2
4
1
3
4
2
1
4
2
3
4
3
1
4
3
2
问题2 由数字1,2,3,4可以组成多少个没有重复数字的三位数?
问题3:问题1、问题2 的共同特点是?能否推广到一般?
问题1和问题2都是研究从一些不同元素中取出部分元素,并按照一定的顺序排成一列的方法数.
(一)排列:一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
问题2:从4个不同的元素a,b,c,d中任取3个,然后按照一定的顺序排成一列.
问题1:从3个不同的元素a,b,c中任意取出2个,并按一定的顺序排成一列.
基本概念
说明:
1、元素不能重复。n个中不能重复,m个中也不能重复.
2、“按一定顺序”就是与位置有关,这是判断一个问题是否是排列问题的关键。
3、两个排列相同,当且仅当这两个排列中的元素完全相同,而且元素的排列顺序也完全相同。
4、m<n时的排列叫选排列,m=n时的排列叫全排列。
5、为了使写出的所有排列情况既不重复也不遗漏,最好采用“树形图”。
相同排列:
当且仅当两个排列的元素相同,顺序也相同时,两个排列相同。
不相同排列:
当两个排列的元素不相同或顺序不相同时,两个排列不相同。
1、123与132、
2、123与124
位置不同
元素不同
学习新知
例1、下列问题中哪些是排列问题?
(1)10名学生中抽2名学生开会
(2)10名学生中选2名做正、副组长
(3)从2,3,5,7,11中任取两个数相乘
(4)从2,3,5,7,11中任取两个数相除
(5)20位同学互通一次电话
(6)有10个车站,共需要多少种车票?
(7)有10个车站,共需要多少种不同的票价?
不是
是
不是
不是
不是
是
是
例题讲评
(8)从高二17班全体同学中选5人组成课外数学学习小组;
(9)从高二18班全体同学中选5人分别参加校运动会的5个不同运动项目;
不是
是
(1)首先要保证元素无重复性,即从n个不同元素中,取出m(m≤n)个不同的元素,否则不是排列问题。
(2)要保证元素的有序性,即安排这m个元素时是有序的,有序就是排列,无序则不是排列.
而检验它是否有序的依据就是变换元素的位置,看结果是否发生变化,有变化是有序,无变化就是无序.
排列问题的判断方法:
例2.四个人A,B,C,D坐成一排照相有多少种坐法?将它们列出来.
解:先安排A有4种坐法,安排B有3种坐法,安排C有2种坐法,安排D有1种坐法,由分步乘法计数原理,有4×3×2×1=24(种).
画出树形图.
若在条件中再增加一条“A不坐排头”,则结论如何?
例题讲评
(二).排列数:
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m个元素的排列数。用符号 表示。
“排列”和“排列数”有什么区别和联系?
“一个排列”是指:从n个不同元素中,任取m个元素按照一定的顺序排成一列,不是数;
“排列数”是指:从n个不同元素中,任取m个元素所有排列的个数,是一个数;所以符号 只表示排列数,而不表示具体的排列.
基本概念
1)问题1:中是求从3个不同元素中取出2个元 素的排列数,记为 ,已经算得
2)问题2:中是求从4个不同元素中取出3个元素的排列数,记为 ,已经算出
3).从n个不同元素中取出2个元素的排列数是多少
呢?
呢?
……
第1位
第2位
第3位
第m位
n种
(n-1)种
(n-2)种
(n-m+1)种
探究:
(三)排列数公式(1):
当m=n时,
正整数1到n的连乘积,叫做n的阶乘,用 表示。
n个不同元素的全排列公式:
排列数公式(2):
说明:
①排列数公式的第一个常用来计算,第二个常用来证明.
为了使当m=n时上面的公式也成立,规定:
②.对于 这个条件要留意,往往是解方程时的隐含条件.
!
n
例3. 计算:
(1)
(2)
(3 )
解:(1)
(3)
(2)
(4)
(4)
例4.证明:
证明:右边
变式练习:
由n=18,n-m+1=8,得m=11
18
11
8
15
几种特殊的排列
1.优先排列
2.集团排列(捆绑法)
3.间隔排列
4.有序排列
综合练习
四.课堂小结:
1.排列:从n个不同元素中选出m(m≤n)个元素,并按
一定的顺序排成一列.
2.关键点:1.互异性(被选、所选元素互不相同)
2.有序性(所选元素有先后位置等顺序之分)
3.排列数:所有排列总数
