8.5.3?平面与平面平行-2021-2022学年高一数学同步精品高效讲练课件(人教A版2019必修第二册)(共28张PPT)
文档属性
| 名称 | 8.5.3?平面与平面平行-2021-2022学年高一数学同步精品高效讲练课件(人教A版2019必修第二册)(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 11:44:33 | ||
图片预览







文档简介
(共28张PPT)
数学
8.5.3 平面与平面平行
同步精品课件
学习目标
XUE XI MU BIAO
问题导入
WEN TI DAO RU
知识梳理
ZHI SHI SHU LI
知识点一 平面与平面平行的判定定理
文字语言 如果一个平面内的 与另一个平面平行,那么这两个平面平行
符号语言
图形语言
两条相交直线
知识点二 两个平面平行的性质定理
文字语言 两个平面平行,如果另一个平面与这两个平面相交,那么两条交线______
符号语言 α∥β,α∩γ=a,β∩γ=b ________
图形语言
平行
a∥b
题型探究
TI XING TAN JIU
一、平面与平面平行的判定定理的应用
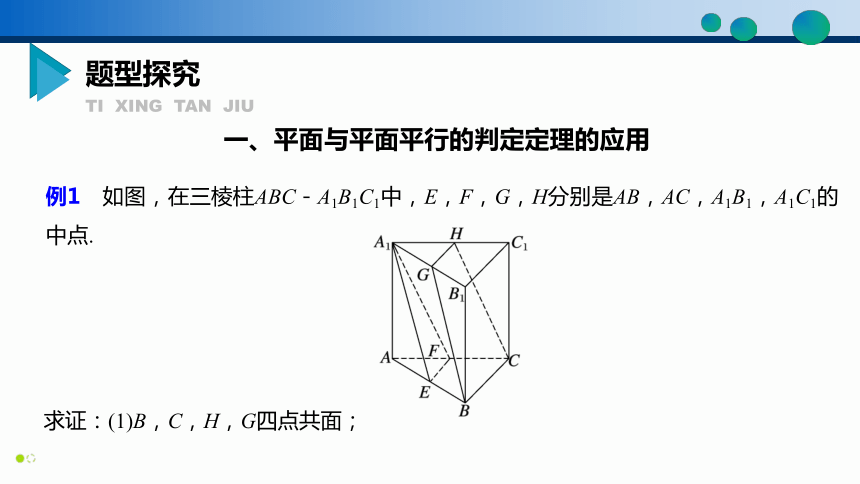
例1 如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.
求证:(1)B,C,H,G四点共面;
证明 ∵GH是△A1B1C1的中位线,∴GH∥B1C1.
又B1C1∥BC,∴GH∥BC,
∴B,C,H,G四点共面.
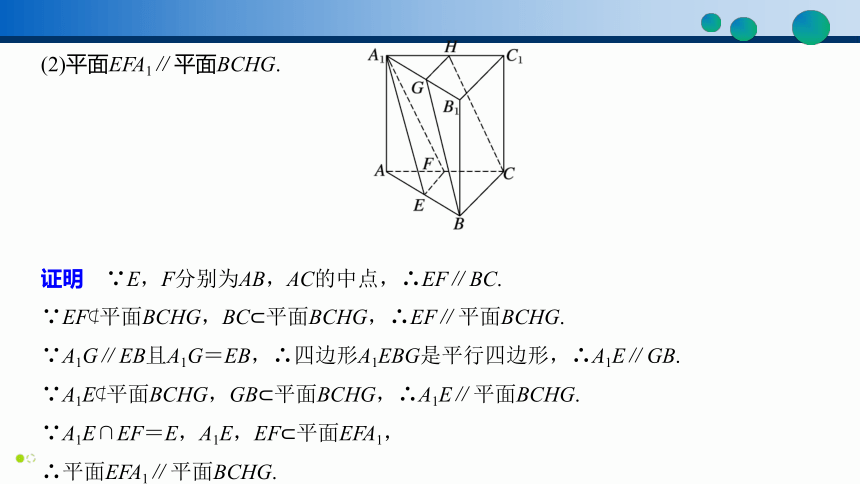
(2)平面EFA1∥平面BCHG.
证明 ∵E,F分别为AB,AC的中点,∴EF∥BC.
∵EF 平面BCHG,BC 平面BCHG,∴EF∥平面BCHG.
∵A1G∥EB且A1G=EB,∴四边形A1EBG是平行四边形,∴A1E∥GB.
∵A1E 平面BCHG,GB 平面BCHG,∴A1E∥平面BCHG.
∵A1E∩EF=E,A1E,EF 平面EFA1,
∴平面EFA1∥平面BCHG.
反思感悟
跟踪训练1 如图,在四棱锥P-ABCD中,E,F,G分别是PC,PD,BC的中点,DC∥AB,求证:平面PAB∥平面EFG.
证明 ∵E,G分别是PC,BC的中点,
∴EG∥PB,
又∵EG 平面PAB,PB 平面PAB,
∴EG∥平面PAB,
∵E,F分别是PC,PD的中点,
∴EF∥CD,又∵AB∥CD,
∴EF∥AB,∵EF 平面PAB,AB 平面PAB,
∴EF∥平面PAB,又EF∩EG=E,EF,EG 平面EFG,
∴平面EFG∥平面PAB.
二、平面与平面平行的性质定理的应用
反思感悟
利用面面平行的性质定理判断两直线平行的步骤
(1)先找两个平面,使这两个平面分别经过这两条直线中的一条.
(2)判定这两个平面平行(此条件有时题目会直接给出).
(3)再找一个平面,使这两条直线都在这个平面上.
(4)由定理得出结论.
跟踪训练2
三、平行关系的综合应用
跟踪训练3
随堂演练
SUI TANG YAN LIAN
3.已知长方体ABCD-A′B′C′D′,平面α∩平面ABCD=EF,平面α∩平面A′B′C′D′=E′F′,则EF与E′F′的位置关系是
A.平行 B.相交
C.异面 D.不确定
解析 由面面平行的性质定理易得A.
4.若平面α∥平面β,直线a α,点M∈β,过点M的所有直线中
A.不一定存在与a平行的直线
B.只有两条与a平行的直线
C.存在无数条与a平行的直线
D.有且只有一条与a平行的直线
解析 由于α∥β,a α,M∈β,过M有且只有一条直线与a平行,故D项正确.
5.已知α,β是两个不同的平面,下列条件中可以判断平面α与β平行的是
(1)α内存在不共线的三点到β的距离相等;
(2)l,m是α内的两条直线,且l∥β,m∥β;
(3)l,m是两条异面直线,且l∥α,m∥α,l∥β,m∥β.
A.(1)(2) B.(1)(3) C.(3) D.(1)(2)(3)
解析 平面α内存在不共线的三点到平面β的距离相等,平面α与平面β可能平行也可能相交,故(1)不正确;
当l与m平行时,不能推出α∥β,故(2)不确定;
l,m是两条异面直线,且l∥α,m∥α,l∥β,m∥β,则α内存在两条相交直线与平面β平行,根据面面平行的判定定理,可得α∥β,故(3)正确.
课堂小结
KE TANG XIAO JIE
1.知识清单:
(1)平面与平面平行的判定定理.
(2)平面与平面平行的性质定理.
2.方法归纳:转化与化归.
3.常见误区:平面与平面平行的条件不充分.
数学
8.5.3 平面与平面平行
同步精品课件
学习目标
XUE XI MU BIAO
问题导入
WEN TI DAO RU
知识梳理
ZHI SHI SHU LI
知识点一 平面与平面平行的判定定理
文字语言 如果一个平面内的 与另一个平面平行,那么这两个平面平行
符号语言
图形语言
两条相交直线
知识点二 两个平面平行的性质定理
文字语言 两个平面平行,如果另一个平面与这两个平面相交,那么两条交线______
符号语言 α∥β,α∩γ=a,β∩γ=b ________
图形语言
平行
a∥b
题型探究
TI XING TAN JIU
一、平面与平面平行的判定定理的应用
例1 如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.
求证:(1)B,C,H,G四点共面;
证明 ∵GH是△A1B1C1的中位线,∴GH∥B1C1.
又B1C1∥BC,∴GH∥BC,
∴B,C,H,G四点共面.
(2)平面EFA1∥平面BCHG.
证明 ∵E,F分别为AB,AC的中点,∴EF∥BC.
∵EF 平面BCHG,BC 平面BCHG,∴EF∥平面BCHG.
∵A1G∥EB且A1G=EB,∴四边形A1EBG是平行四边形,∴A1E∥GB.
∵A1E 平面BCHG,GB 平面BCHG,∴A1E∥平面BCHG.
∵A1E∩EF=E,A1E,EF 平面EFA1,
∴平面EFA1∥平面BCHG.
反思感悟
跟踪训练1 如图,在四棱锥P-ABCD中,E,F,G分别是PC,PD,BC的中点,DC∥AB,求证:平面PAB∥平面EFG.
证明 ∵E,G分别是PC,BC的中点,
∴EG∥PB,
又∵EG 平面PAB,PB 平面PAB,
∴EG∥平面PAB,
∵E,F分别是PC,PD的中点,
∴EF∥CD,又∵AB∥CD,
∴EF∥AB,∵EF 平面PAB,AB 平面PAB,
∴EF∥平面PAB,又EF∩EG=E,EF,EG 平面EFG,
∴平面EFG∥平面PAB.
二、平面与平面平行的性质定理的应用
反思感悟
利用面面平行的性质定理判断两直线平行的步骤
(1)先找两个平面,使这两个平面分别经过这两条直线中的一条.
(2)判定这两个平面平行(此条件有时题目会直接给出).
(3)再找一个平面,使这两条直线都在这个平面上.
(4)由定理得出结论.
跟踪训练2
三、平行关系的综合应用
跟踪训练3
随堂演练
SUI TANG YAN LIAN
3.已知长方体ABCD-A′B′C′D′,平面α∩平面ABCD=EF,平面α∩平面A′B′C′D′=E′F′,则EF与E′F′的位置关系是
A.平行 B.相交
C.异面 D.不确定
解析 由面面平行的性质定理易得A.
4.若平面α∥平面β,直线a α,点M∈β,过点M的所有直线中
A.不一定存在与a平行的直线
B.只有两条与a平行的直线
C.存在无数条与a平行的直线
D.有且只有一条与a平行的直线
解析 由于α∥β,a α,M∈β,过M有且只有一条直线与a平行,故D项正确.
5.已知α,β是两个不同的平面,下列条件中可以判断平面α与β平行的是
(1)α内存在不共线的三点到β的距离相等;
(2)l,m是α内的两条直线,且l∥β,m∥β;
(3)l,m是两条异面直线,且l∥α,m∥α,l∥β,m∥β.
A.(1)(2) B.(1)(3) C.(3) D.(1)(2)(3)
解析 平面α内存在不共线的三点到平面β的距离相等,平面α与平面β可能平行也可能相交,故(1)不正确;
当l与m平行时,不能推出α∥β,故(2)不确定;
l,m是两条异面直线,且l∥α,m∥α,l∥β,m∥β,则α内存在两条相交直线与平面β平行,根据面面平行的判定定理,可得α∥β,故(3)正确.
课堂小结
KE TANG XIAO JIE
1.知识清单:
(1)平面与平面平行的判定定理.
(2)平面与平面平行的性质定理.
2.方法归纳:转化与化归.
3.常见误区:平面与平面平行的条件不充分.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
