2012年高考试题分析及2013年复习备考建议——立体几何与解析几何
文档属性
| 名称 | 2012年高考试题分析及2013年复习备考建议——立体几何与解析几何 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-25 00:00:00 | ||
图片预览





文档简介
课件43张PPT。高密市康成中学管目军2012年高考试题分析
及2013年复习备考建议
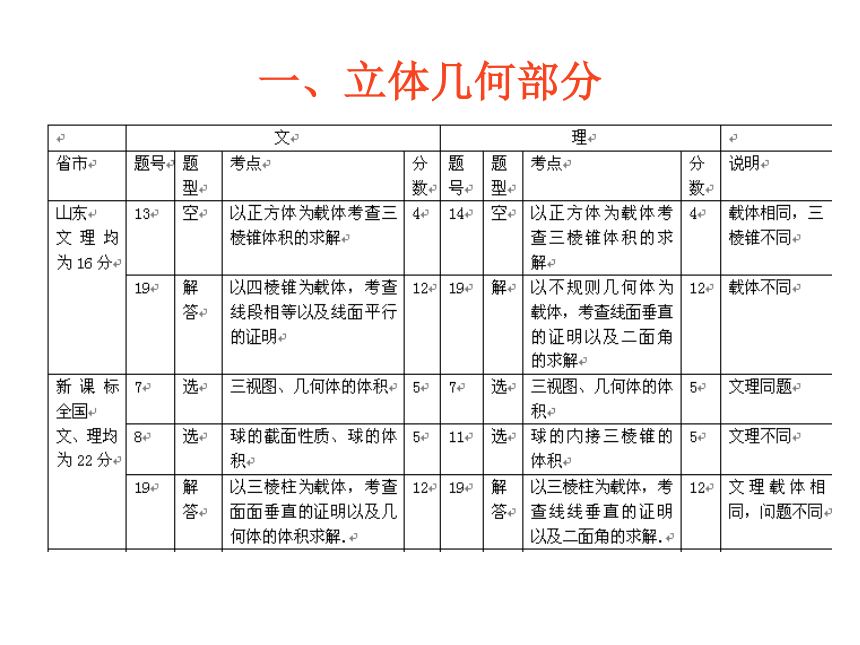
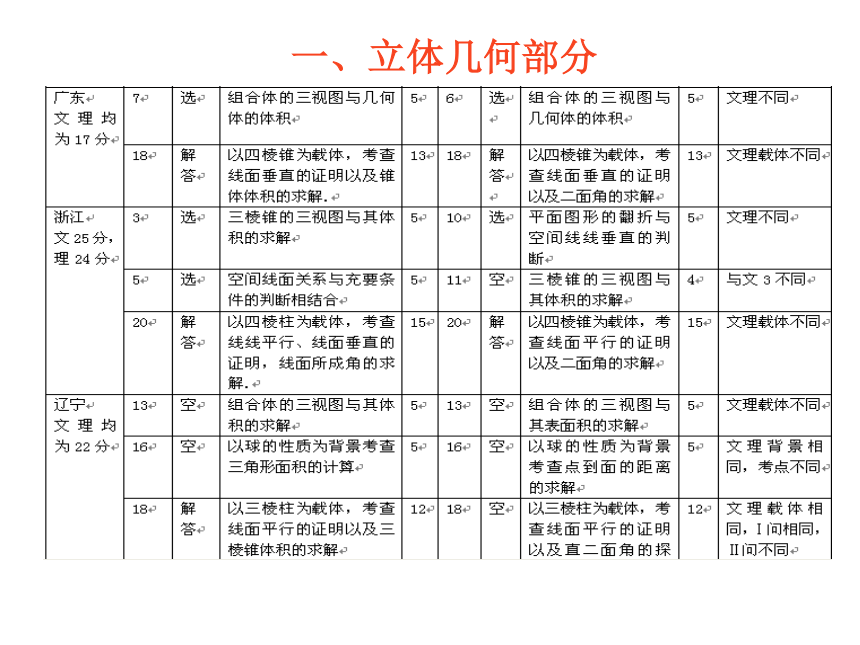
——立体几何与解析几何一、立体几何部分1、新课标各地高考分数统计一、立体几何部分 一、立体几何部分 文科在这部分内容中,共学习必修2两章按课程标准规定的课时数,文科数学总课时数是252课时,这两章的课时数是18课时,约占7%,试卷中期望的分数应是11分.山东和广东都考了一个小题,一个大题,分值:山东16分,广东18分;而全国新课程卷考查了两个小题一个大题,分值达到了22分.可见这部分的知识虽然课时数不多,但是份量却不轻.
理科在这部分内容中,共学习必修2两章,选修2-1一章共计三章按课程标准规定的课时数,理科数学总课时数是288课时,这两章的课时数是30课时,约占10%,试卷中期望的分数是15分,应是一个小题,一个大题. 考题与分数值同文科一致,所以说山东、广东的基本符合这个期望值,而全国新课程的试题中这部分的分量有所加重.
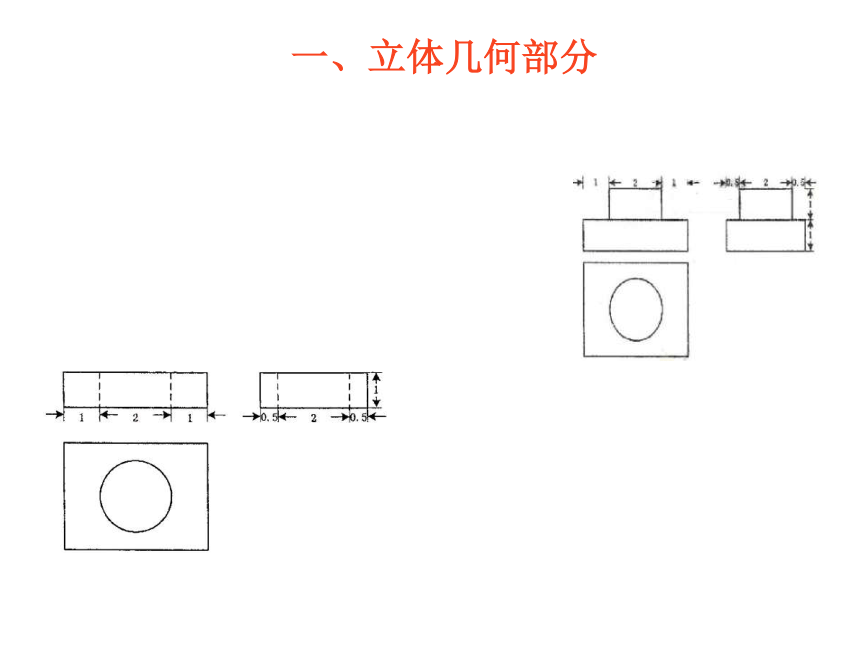
三份试题中对于对于重点内容都进行了重点考查,如线线、线面的平行与垂直、二面角等等,另外对于课标教材新增知识——三视图,除山东卷外,其余两套试卷都有所考查.一、立体几何部分二、三视图的考查仍是客观题命题的热点,但考查形式呈现多样化:一是几何体三视图的识别与判断;二是简单几何体的三视图与几何体的表面积、体积的求解相结合;三是组合体的三视图识别与几何体的表面积、体积的求解的综合.1. 几何体三视图的识别与判断
【典例1】(2102高考福建,4)一个几何体的三视图形状都相同,大小均等,那么这个几何体不可以是( )
A 球 B 三棱锥 C 正方体 D 圆柱
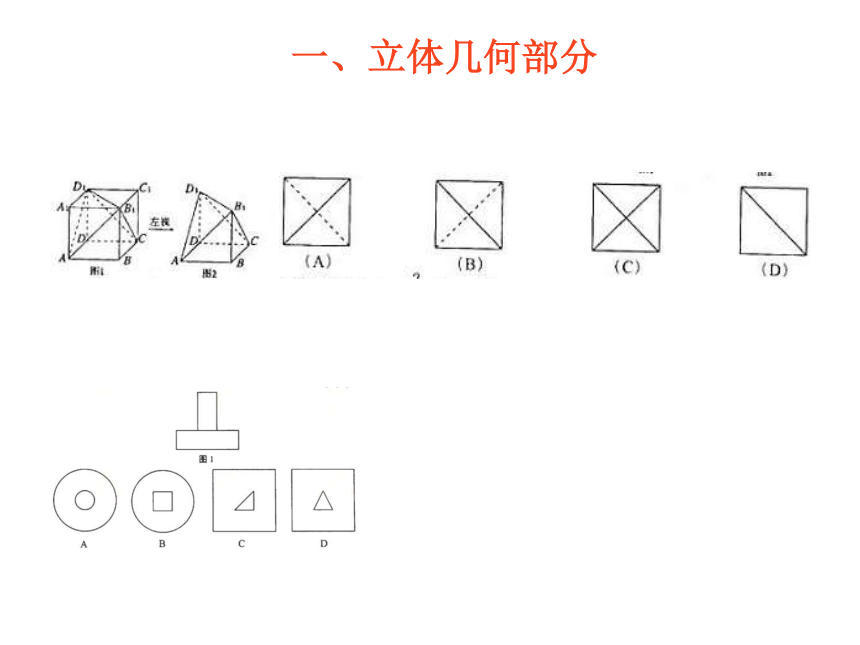
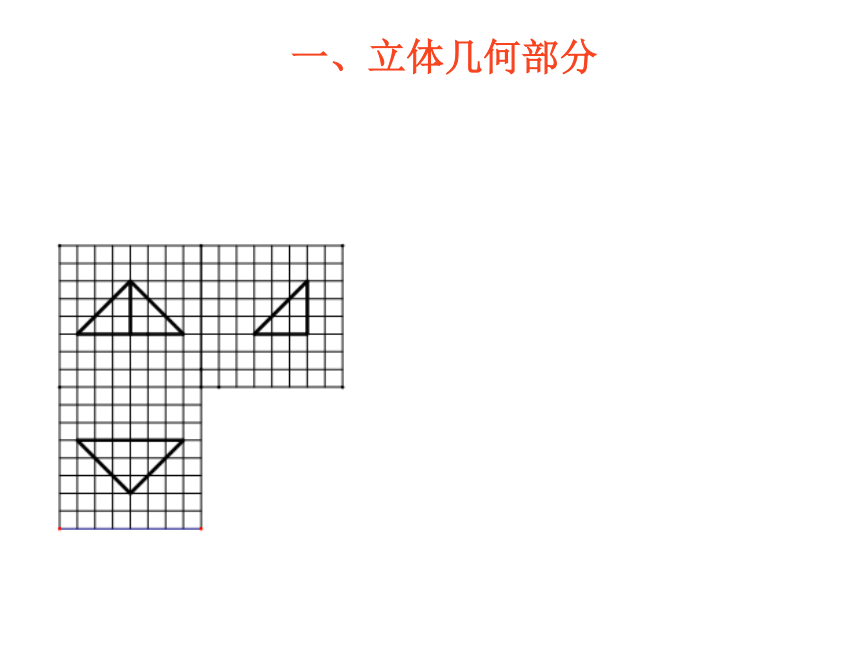
【分析】本题考查了空间几何体的形状和三视图的概念,以及考生的空间想象能力.一、立体几何部分【典例2】(2012高考陕西,文8)将正方形(如图所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为 ( )【解析】本题主要考查几何体三视图的识别.【典例3】(2012高考真题湖南,理3文4)某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是【分析】本题主要考查组合体的三视图识别.一、立体几何部分2.简单几何体的三视图与其表面积、体积的综合【典例1】(2012高考新课标,7)如图,网格纸上小正方形的边长为,粗线画出的是某几何体的三视图,则此几何体的体积为( )
A.6 B.9 C.12 D.18【分析】该题主要考查了三棱锥的三视图的识别与其体积的求解.一、立体几何部分【典例2】(2012高考浙江,文3)已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积是
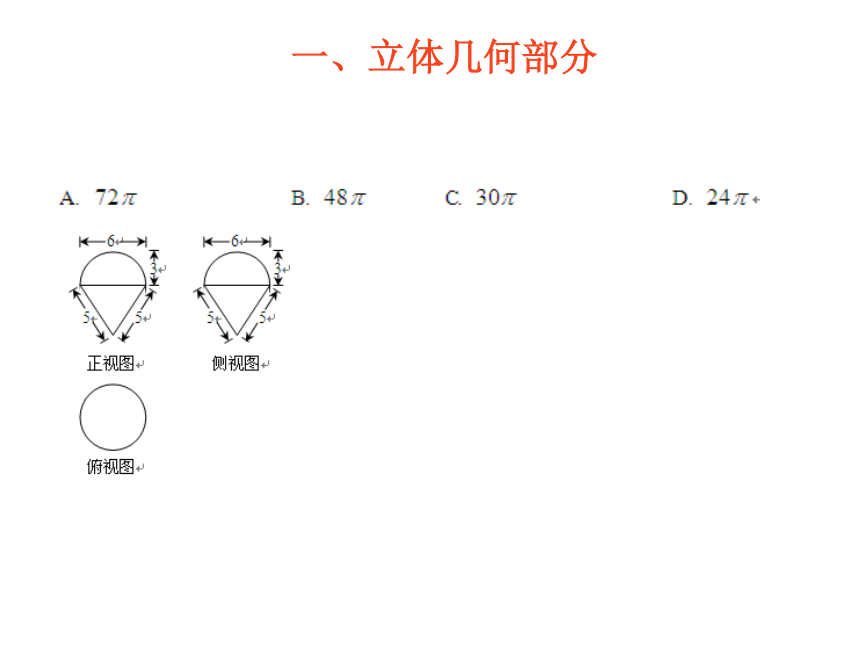
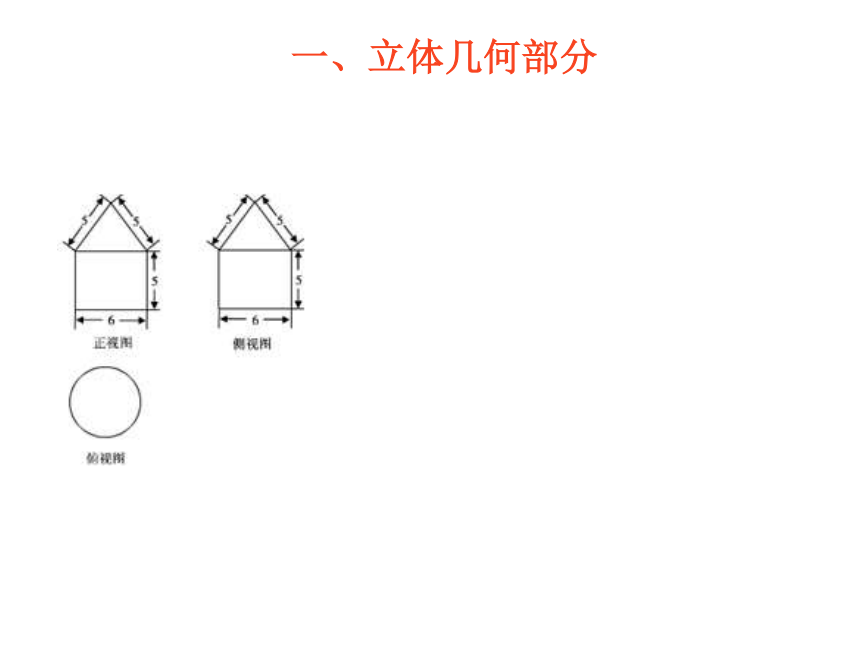
A.1cm3 B.2cm3 C.3cm3 D.6cm3【解析】该题主要考查三棱锥的三视图识别与其体积的求解. 【典例3】(2012高考浙江,理11)已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积等于________cm3. 【解析】该题主要考查三棱锥的三视图识别与其体积的求解.一、立体几何部分3. 组合体的三视图识别与几何体的表面积、体积的求解的综合【典例1】(2012高考辽宁,文13)一个几何体的三视图如图所示,则该几何体的体积为_______________.【分析】本题主要考查组合体的三视图、柱体的体积公式。【典例2】(2012高考辽宁,理13)一个几何体的三视图如图所示,则该几何体的表面积为______________。【分析】本题主要考查组合体的三视图、柱体的表面积公式。一、立体几何部分 【典例3】(2012高考广东,文7)某几何体的三视图如图所示,它的体积为【分析】本题主要考查组合体的三视图以及球体和锥体体积的求解.一、立体几何部分 【典例4】(2012高考广东,理6)某几何体的三视图如图所示,它的体积为
A.12π B.45π C.57π D.81π【分析】本题主要考查组合体的三视图以及柱体和锥体体积的求解.一、立体几何部分 【典例5】(2012高考天津,文10)一个几何体的三视图如图所示(单位:m),则该几何体的体积 .【分析】本题主要考查组合体的三视图以及柱体体积的求解.一、立体几何部分 命题的趋势与预测:试题的难度逐步降低,几何体的结构特征与三视图的识别是命题的热点,空间线面关系的判断往往与充要条件的判断相结合. 预计2013年的山东高考命题中,立体几何的客观题仍然只有一道,命题的重点应为简单几何体的三视图与几何体的表面积、体积相结合.一、立体几何部分 三、空间线面关系的逻辑证明是文理解答题共同关注的焦点,文科以空间线面平行与垂直的证明、几何体的体积、表面积的求解为命题重点;理科第1问均为空间线面关系的证明——多为线面平行的证明,(2)问命题的热点是二面角的求解,并且根据几何体的结构特征很容易建立空间直角坐标系,将二面角的求解转化为空间向量的有关运算.但命题的载体多样化,以锥体与柱体为重点.1.文科重在空间线面关系的逻辑证明,与几何体的表面积、体积等问题综合【分析】本题以棱锥为载体主要考查空间线面关系的逻辑证明,考查了空间想象能力以及基本的推理证明能力.一、立体几何部分【分析】本题以棱柱为载体主要考查空间面面垂直的逻辑证明,空间几何体的体积等,考查了空间想象能力以及基本的推理证明能力.【分析】本题以棱锥为载体主要考查空间线面垂直的逻辑证明,空间几何体的体积等,考查了空间想象能力以及基本的推理证明能力.一、立体几何部分 【分析】本题以长方体为载体主要考查几何体体积的求解以及以及空间线面垂直的证明、平面图形的翻折问题,考查了空间想象能力以及基本的推理证明能力.一、立体几何部分 2. 理科重在空间角的求解,尤其是二面角的求解仍是高考命题的热点.【分析】该题以不规则几何体为载体考查空间线面垂直的证明以及二面角的求解.一、立体几何部分 【分析】该题以棱柱为载体主要考查空间线线垂直的证明以及二面角的求解.一、立体几何部分 【分析】该题以棱锥为载体考查空间线面垂直的证明以及二面角的求解.一、立体几何部分 【分析】该题以长方体为载体主要考查空间线线垂直、空间线面平行关系的探究性问题以及二面角的求解.一、立体几何部分 【分析】该题以平面图形的翻折为背景,考查了空间线线垂直的证明、线段长度的求解以及二面角的求解等.一、立体几何部分 近几年高考试题分析:
从近几年高考试题来看,几何体按照柱体和锥体交替出现的规律,但近几年的高考试题中,台体与不规则几何体成为命题的载体;命题的趋势与预测:(1)命题的载体逐步趋向不规则几何体,有意识地加强对空间几何体结构特征的认识和空间想象能力的考查;(2)几何载体也趋向文理有别;(3)在空间线面关系的证明过程中渗透空间几何体中的一些基本运算;(4)注意几何体中的一些运算在其它问题中的渗透,如空间线面角、线线角与空间距离的求解等.预计2013年的山东高考命题中,总体上试题的难度基本保持不变,命题的几何载体可能为不规则的几何体(或组合体),文科仍会坚持以空间线面关系的推理证明、几何体的体积求解为主;理科坚持以空间线面关系的推理证明与二面角的求解为主. 一、立体几何部分 复习备考建议1.认真研究考试说明和高考试题和新教材,把握好复习的方向.
2.夯实基础,狠抓规范
基础知识、基本技能、基本方法、基础练习要到位, 立体几何的基本概念、公理、定理是基础;解题步骤要规范;注重通性通法,体现“大众化”.
3.注重数学方法,加强学法指导
转化、化归的思想贯穿立体几何的始终,是处理立体几何问题的基本思想.另外还要注意提高识图、理解图、应用图的能力,解题时应多画、多看、多想,这样才能提高空间想象能力和解决问题的能力.
4.理科注意合理建立坐标系,突出向量方法二、解析几何部分 1、新课标各地高考分数统计 二、解析几何部分 二、解析几何部分 文科在这块内容中,共学习必修2两章:直线与方程、圆与方程,选修1—1:圆锥曲线与方程这三章,按课程标准规定的课时数,文科数学总课时数是252课时,这三章的课时数是30课时,占12%,试卷中的期望分数应是18分.
山东21分比较吻合, 全国新课程卷文22分稍高于这个期望分数;广东文19分比较吻合.
理科在这块内容中,也共学习必修2两章:直线与方程、圆与方程,选修2—1:圆锥曲线与方程这三章,按课程标准规定的课时数,理科数学总课时数是288课时,这三章的课时数是28课时,占10%,试卷中的期望分数应是15分.
山东17分,广东14分比较吻合,全国新课程22分高于这个期望分数.二、解析几何部分 2、直线和圆 直线和圆部分命题主要以选择、填空题的形式命题,命题以直线和圆的位置关系为中心,涉及圆的方程的求解、直线被圆所截弦长、直线和圆的位置关系判断、圆与圆的位置关系判断等,试题比较简单.二、解析几何部分 二、解析几何部分 二、解析几何部分3、圆锥曲线 1.客观题主要考查椭圆、双曲线、抛物线的定义方程、性质及其基本运算.试题多为基础性的综合题,圆锥曲线与圆相结合、椭圆与双曲线、椭圆与抛物线相结合等,但试题的难度降低,文理有比较明显的区别,多以圆、椭圆、抛物线和双曲线中两种曲线的小综合问题为主,近几年高考试题逐步摆脱与向量的结合,以知识模块内的综合为主.二、解析几何部分 二、解析几何部分 二、解析几何部分 二、解析几何部分 2. 解答题命题的重点椭圆,山东卷多为最后一题,作为压轴题出现的.从考查内容来看,均以椭圆或椭圆与圆、抛物线、双曲线问题相结合的出现,但考查的重点在与直线和椭圆的位置关系以及定点定值、最值与范围的考查,近两年高考试题文理均注重对某类圆锥曲线中的有关性质进行深入挖掘,以相关性质的推导与证明及其应用为主,根据近几年命题的趋势来看,2013年的高考试题中解析几何的解答题有可能仍以压轴题的形式出现,但试题入门较低,问题逐步深入,体现高考命题的“选拨”功能.二、解析几何部分 二、解析几何部分 二、解析几何部分 二、解析几何部分 二、解析几何部分 二、解析几何部分 二、解析几何部分 二、解析几何部分复习备考建议:
1.认真研究考试说明和高考试题和新教材,把握好复习的方向.
2.研究学生,以学生的学来确定教师的教,增强教学的针对性.
3.提高应用数学思想方法(特别是数形结合)解决问题的熟练程度;要认真审题,挖掘题目的几何意义,寻找合理的运算途径并注重整体运算 .
4.突出抓好重点、热点考查内容的复习.
5.加强直线与圆锥曲线的位置关系的复习.直线与圆锥曲线的位置关系一直为高考的热点,这类问题常涉及圆锥曲线的性质和直线的基本知识点,有时往往和平面向量相结合,因此分析问题时要利用数形结合的思想、函数与方程的思想、坐标法等,达到优化解题思路、简化解题过程的目的.二、解析几何部分 谢谢!
及2013年复习备考建议
——立体几何与解析几何一、立体几何部分1、新课标各地高考分数统计一、立体几何部分 一、立体几何部分 文科在这部分内容中,共学习必修2两章按课程标准规定的课时数,文科数学总课时数是252课时,这两章的课时数是18课时,约占7%,试卷中期望的分数应是11分.山东和广东都考了一个小题,一个大题,分值:山东16分,广东18分;而全国新课程卷考查了两个小题一个大题,分值达到了22分.可见这部分的知识虽然课时数不多,但是份量却不轻.
理科在这部分内容中,共学习必修2两章,选修2-1一章共计三章按课程标准规定的课时数,理科数学总课时数是288课时,这两章的课时数是30课时,约占10%,试卷中期望的分数是15分,应是一个小题,一个大题. 考题与分数值同文科一致,所以说山东、广东的基本符合这个期望值,而全国新课程的试题中这部分的分量有所加重.
三份试题中对于对于重点内容都进行了重点考查,如线线、线面的平行与垂直、二面角等等,另外对于课标教材新增知识——三视图,除山东卷外,其余两套试卷都有所考查.一、立体几何部分二、三视图的考查仍是客观题命题的热点,但考查形式呈现多样化:一是几何体三视图的识别与判断;二是简单几何体的三视图与几何体的表面积、体积的求解相结合;三是组合体的三视图识别与几何体的表面积、体积的求解的综合.1. 几何体三视图的识别与判断
【典例1】(2102高考福建,4)一个几何体的三视图形状都相同,大小均等,那么这个几何体不可以是( )
A 球 B 三棱锥 C 正方体 D 圆柱
【分析】本题考查了空间几何体的形状和三视图的概念,以及考生的空间想象能力.一、立体几何部分【典例2】(2012高考陕西,文8)将正方形(如图所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为 ( )【解析】本题主要考查几何体三视图的识别.【典例3】(2012高考真题湖南,理3文4)某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是【分析】本题主要考查组合体的三视图识别.一、立体几何部分2.简单几何体的三视图与其表面积、体积的综合【典例1】(2012高考新课标,7)如图,网格纸上小正方形的边长为,粗线画出的是某几何体的三视图,则此几何体的体积为( )
A.6 B.9 C.12 D.18【分析】该题主要考查了三棱锥的三视图的识别与其体积的求解.一、立体几何部分【典例2】(2012高考浙江,文3)已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积是
A.1cm3 B.2cm3 C.3cm3 D.6cm3【解析】该题主要考查三棱锥的三视图识别与其体积的求解. 【典例3】(2012高考浙江,理11)已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积等于________cm3. 【解析】该题主要考查三棱锥的三视图识别与其体积的求解.一、立体几何部分3. 组合体的三视图识别与几何体的表面积、体积的求解的综合【典例1】(2012高考辽宁,文13)一个几何体的三视图如图所示,则该几何体的体积为_______________.【分析】本题主要考查组合体的三视图、柱体的体积公式。【典例2】(2012高考辽宁,理13)一个几何体的三视图如图所示,则该几何体的表面积为______________。【分析】本题主要考查组合体的三视图、柱体的表面积公式。一、立体几何部分 【典例3】(2012高考广东,文7)某几何体的三视图如图所示,它的体积为【分析】本题主要考查组合体的三视图以及球体和锥体体积的求解.一、立体几何部分 【典例4】(2012高考广东,理6)某几何体的三视图如图所示,它的体积为
A.12π B.45π C.57π D.81π【分析】本题主要考查组合体的三视图以及柱体和锥体体积的求解.一、立体几何部分 【典例5】(2012高考天津,文10)一个几何体的三视图如图所示(单位:m),则该几何体的体积 .【分析】本题主要考查组合体的三视图以及柱体体积的求解.一、立体几何部分 命题的趋势与预测:试题的难度逐步降低,几何体的结构特征与三视图的识别是命题的热点,空间线面关系的判断往往与充要条件的判断相结合. 预计2013年的山东高考命题中,立体几何的客观题仍然只有一道,命题的重点应为简单几何体的三视图与几何体的表面积、体积相结合.一、立体几何部分 三、空间线面关系的逻辑证明是文理解答题共同关注的焦点,文科以空间线面平行与垂直的证明、几何体的体积、表面积的求解为命题重点;理科第1问均为空间线面关系的证明——多为线面平行的证明,(2)问命题的热点是二面角的求解,并且根据几何体的结构特征很容易建立空间直角坐标系,将二面角的求解转化为空间向量的有关运算.但命题的载体多样化,以锥体与柱体为重点.1.文科重在空间线面关系的逻辑证明,与几何体的表面积、体积等问题综合【分析】本题以棱锥为载体主要考查空间线面关系的逻辑证明,考查了空间想象能力以及基本的推理证明能力.一、立体几何部分【分析】本题以棱柱为载体主要考查空间面面垂直的逻辑证明,空间几何体的体积等,考查了空间想象能力以及基本的推理证明能力.【分析】本题以棱锥为载体主要考查空间线面垂直的逻辑证明,空间几何体的体积等,考查了空间想象能力以及基本的推理证明能力.一、立体几何部分 【分析】本题以长方体为载体主要考查几何体体积的求解以及以及空间线面垂直的证明、平面图形的翻折问题,考查了空间想象能力以及基本的推理证明能力.一、立体几何部分 2. 理科重在空间角的求解,尤其是二面角的求解仍是高考命题的热点.【分析】该题以不规则几何体为载体考查空间线面垂直的证明以及二面角的求解.一、立体几何部分 【分析】该题以棱柱为载体主要考查空间线线垂直的证明以及二面角的求解.一、立体几何部分 【分析】该题以棱锥为载体考查空间线面垂直的证明以及二面角的求解.一、立体几何部分 【分析】该题以长方体为载体主要考查空间线线垂直、空间线面平行关系的探究性问题以及二面角的求解.一、立体几何部分 【分析】该题以平面图形的翻折为背景,考查了空间线线垂直的证明、线段长度的求解以及二面角的求解等.一、立体几何部分 近几年高考试题分析:
从近几年高考试题来看,几何体按照柱体和锥体交替出现的规律,但近几年的高考试题中,台体与不规则几何体成为命题的载体;命题的趋势与预测:(1)命题的载体逐步趋向不规则几何体,有意识地加强对空间几何体结构特征的认识和空间想象能力的考查;(2)几何载体也趋向文理有别;(3)在空间线面关系的证明过程中渗透空间几何体中的一些基本运算;(4)注意几何体中的一些运算在其它问题中的渗透,如空间线面角、线线角与空间距离的求解等.预计2013年的山东高考命题中,总体上试题的难度基本保持不变,命题的几何载体可能为不规则的几何体(或组合体),文科仍会坚持以空间线面关系的推理证明、几何体的体积求解为主;理科坚持以空间线面关系的推理证明与二面角的求解为主. 一、立体几何部分 复习备考建议1.认真研究考试说明和高考试题和新教材,把握好复习的方向.
2.夯实基础,狠抓规范
基础知识、基本技能、基本方法、基础练习要到位, 立体几何的基本概念、公理、定理是基础;解题步骤要规范;注重通性通法,体现“大众化”.
3.注重数学方法,加强学法指导
转化、化归的思想贯穿立体几何的始终,是处理立体几何问题的基本思想.另外还要注意提高识图、理解图、应用图的能力,解题时应多画、多看、多想,这样才能提高空间想象能力和解决问题的能力.
4.理科注意合理建立坐标系,突出向量方法二、解析几何部分 1、新课标各地高考分数统计 二、解析几何部分 二、解析几何部分 文科在这块内容中,共学习必修2两章:直线与方程、圆与方程,选修1—1:圆锥曲线与方程这三章,按课程标准规定的课时数,文科数学总课时数是252课时,这三章的课时数是30课时,占12%,试卷中的期望分数应是18分.
山东21分比较吻合, 全国新课程卷文22分稍高于这个期望分数;广东文19分比较吻合.
理科在这块内容中,也共学习必修2两章:直线与方程、圆与方程,选修2—1:圆锥曲线与方程这三章,按课程标准规定的课时数,理科数学总课时数是288课时,这三章的课时数是28课时,占10%,试卷中的期望分数应是15分.
山东17分,广东14分比较吻合,全国新课程22分高于这个期望分数.二、解析几何部分 2、直线和圆 直线和圆部分命题主要以选择、填空题的形式命题,命题以直线和圆的位置关系为中心,涉及圆的方程的求解、直线被圆所截弦长、直线和圆的位置关系判断、圆与圆的位置关系判断等,试题比较简单.二、解析几何部分 二、解析几何部分 二、解析几何部分3、圆锥曲线 1.客观题主要考查椭圆、双曲线、抛物线的定义方程、性质及其基本运算.试题多为基础性的综合题,圆锥曲线与圆相结合、椭圆与双曲线、椭圆与抛物线相结合等,但试题的难度降低,文理有比较明显的区别,多以圆、椭圆、抛物线和双曲线中两种曲线的小综合问题为主,近几年高考试题逐步摆脱与向量的结合,以知识模块内的综合为主.二、解析几何部分 二、解析几何部分 二、解析几何部分 二、解析几何部分 2. 解答题命题的重点椭圆,山东卷多为最后一题,作为压轴题出现的.从考查内容来看,均以椭圆或椭圆与圆、抛物线、双曲线问题相结合的出现,但考查的重点在与直线和椭圆的位置关系以及定点定值、最值与范围的考查,近两年高考试题文理均注重对某类圆锥曲线中的有关性质进行深入挖掘,以相关性质的推导与证明及其应用为主,根据近几年命题的趋势来看,2013年的高考试题中解析几何的解答题有可能仍以压轴题的形式出现,但试题入门较低,问题逐步深入,体现高考命题的“选拨”功能.二、解析几何部分 二、解析几何部分 二、解析几何部分 二、解析几何部分 二、解析几何部分 二、解析几何部分 二、解析几何部分 二、解析几何部分复习备考建议:
1.认真研究考试说明和高考试题和新教材,把握好复习的方向.
2.研究学生,以学生的学来确定教师的教,增强教学的针对性.
3.提高应用数学思想方法(特别是数形结合)解决问题的熟练程度;要认真审题,挖掘题目的几何意义,寻找合理的运算途径并注重整体运算 .
4.突出抓好重点、热点考查内容的复习.
5.加强直线与圆锥曲线的位置关系的复习.直线与圆锥曲线的位置关系一直为高考的热点,这类问题常涉及圆锥曲线的性质和直线的基本知识点,有时往往和平面向量相结合,因此分析问题时要利用数形结合的思想、函数与方程的思想、坐标法等,达到优化解题思路、简化解题过程的目的.二、解析几何部分 谢谢!
同课章节目录
