6.2向心力课件 (共22张PPT)
文档属性
| 名称 | 6.2向心力课件 (共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-11 15:31:45 | ||
图片预览






文档简介
(共22张PPT)
6.2 向心力
1:合力为零,物体静止或匀速直线运动
2:匀速圆周运动是一种变速运动
3:做匀速圆周运动的物体一定受力
温故知新
做匀速圆周运动的物体,合力有何特点?
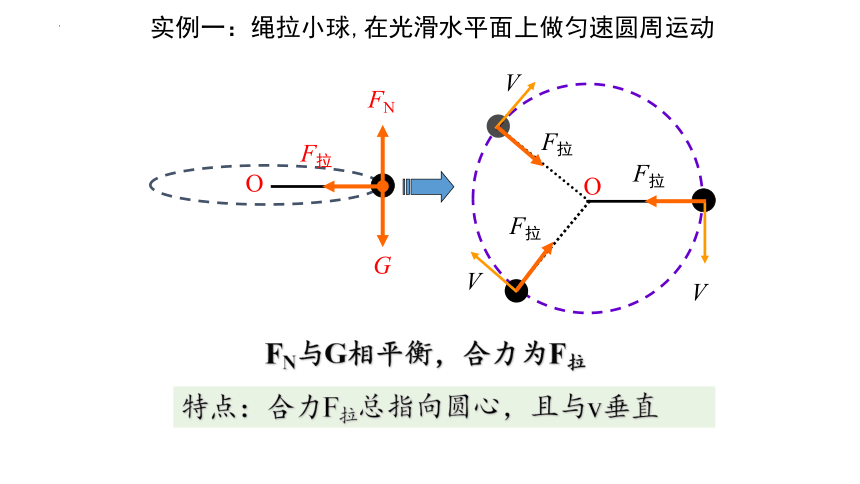
实例一:绳拉小球,在光滑水平面上做匀速圆周运动
O
G
FN
F拉
O
O
F拉
F拉
F拉
V
V
V
O
实例一:绳拉小球,在光滑水平面上做匀速圆周运动
FN与G相平衡,合力为F拉
特点:合力F拉总指向圆心,且与v垂直
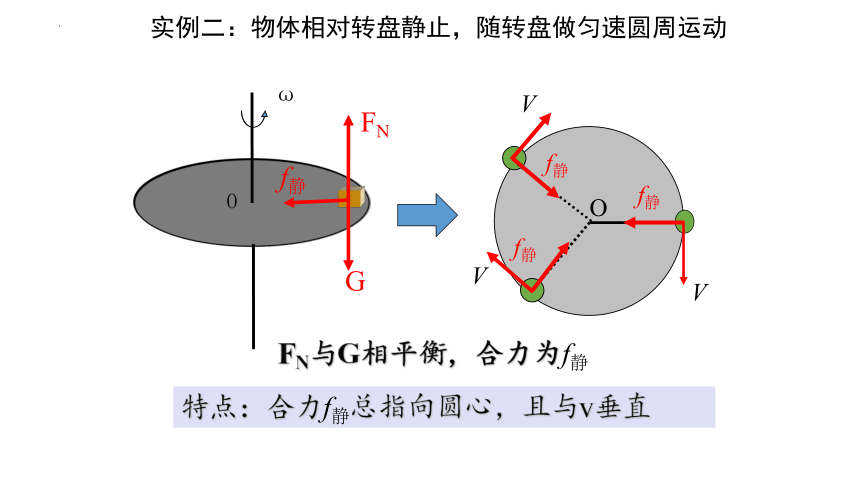
实例二:物体相对转盘静止,随转盘做匀速圆周运动
G
ω
O
FN
f静
实例二:物体相对转盘静止,随转盘做匀速圆周运动
O
f静
f静
f静
V
V
V
FN与G相平衡,合力为f静
特点:合力f静总指向圆心,且与v垂直
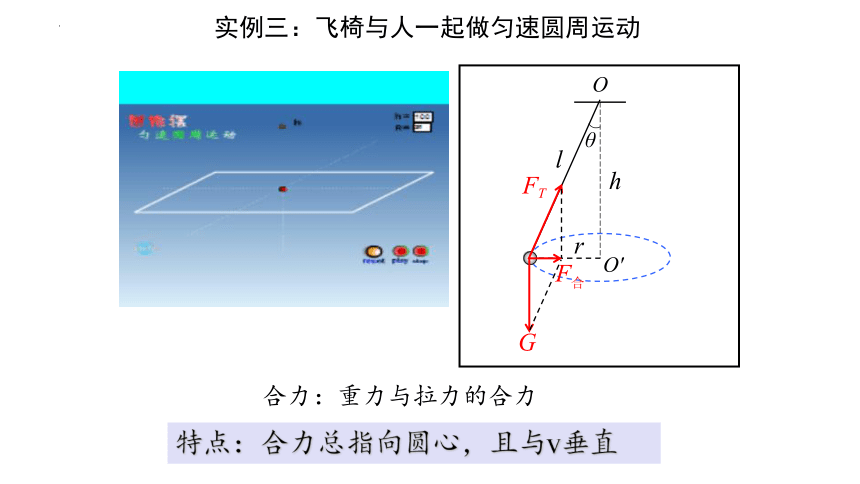
实例三:飞椅与人一起做匀速圆周运动
r
O'
O
θ
l
h
FT
G
F合
合力:重力与拉力的合力
实例三:飞椅与人一起做匀速圆周运动
特点:合力总指向圆心,且与v垂直
合力总指向圆心
整合归纳
合力f静总指向圆心
合力F拉总指向圆心
向心力为
重力与拉力的合力
向心力为f静
向心力为F拉
2、方向:
1、定义:
一、向心力
做匀速圆周运动的物体受到的合外力指向圆心,这个力叫做向心力。
总指向圆心,与速度垂直,方向不断变化。
3、向心力的作用效果:只改变速度的方向,不改变速度的大小。
那它是不是一种新力?
G
Ff
FN
ω
物块随着圆桶一起匀速转动时,物块的受力?物块向心力的来源
物块做匀速圆周运动时,合力提供向心力,即桶对物块的支持力。
匀速圆周运动实例分析——向心力的来源
总结:
向心力的来源:可以是重力、弹力、摩擦力等各种性质的力,也可以是几个力的合力,还可以是某个力的分力。
物体做匀速圆周运动时,由合力提供向心力。
向心力不是物体真实受到的一个力,不能说物体受到向心力的作用 ,只能说某个力或某几个力提供了向心力。
二、向心力的大小
例2. 小球做圆锥摆时细绳长L,与竖直方向成θ角,求小球做匀速圆周运动的向心力和角速度ω。
O’
O
mg
T
F
θ
L
小球做圆周运动的半径
由牛顿第二定律:
即:
R
解析:小球的向心力由T和G的合力提供
变式.如图所示,一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
A.球A的线速度一定大于球B的线速度
B.球A的角速度一定小于球B的角速度
C.球A的运动周期一定小于球B的运动周期
D.球A对筒壁的压力一定大于球B对筒壁的压力
mg
N
F
AB
v
1、做变速圆周运动的物体所受的合力特点:
F
Fn
Ft
Ft 切向分力,它产生切向加速度,改变速度的大小.
Fn 向心分力,它产生向心加速度,改变速度的方向.
加速
①F与V夹角为锐角时做加速圆周运动
②F与V夹角为直角时做匀速圆周运动
③F与V夹角为钝角时做减速圆周运动
把一般曲线分割为许多极短的小段,每一段都可以看作为一小段圆弧,而这些圆弧的弯曲程度不一样,表明它们具有不同的曲率半径。在注意到这点区别之后,分析质点经过曲线上某位置的运动时,就可以采用圆周运动的分析方法对一般曲线运动进行处理了。
r1
r2
2、处理一般曲线运动的方法:
匀速圆周运动:
非匀速圆周运动:
F向是F合的指向圆心方向的分力Fn
向心力的来源:可以是重力、弹力、摩擦力等各种性质的力,也可以是几个力的合力,还可以是某个力的分力。
物体做匀速圆周运动时,由合力提供向心力。
小结
例、一辆汽车在水平公路上转弯,沿曲线由M向N行驶,速度逐渐减小.如图所示,分别画出了汽车转弯时所受合力的四种方向,你认为正确的是( )
A B C D
1.如图所示,汽车在一水平公路上转弯时,汽车的运动可视为匀速圆周运动。下列关于汽车转弯时的说法正确的是( )
A.汽车处于平衡状态 B.汽车的向心力由重力和支持力提供
C.汽车的向心力由摩擦力提供 D.汽车的向心力由支持力提供
C
C
2.甲、乙两物体做匀速圆周运动,其质量之比为1:2,转动半径之比为1:2,在相等时间里甲转过60°,乙转过45°,则它们所受合外力之比为( )
A.1:4 B.2:3 C.4:9 D.9:16
C
6.2 向心力
1:合力为零,物体静止或匀速直线运动
2:匀速圆周运动是一种变速运动
3:做匀速圆周运动的物体一定受力
温故知新
做匀速圆周运动的物体,合力有何特点?
实例一:绳拉小球,在光滑水平面上做匀速圆周运动
O
G
FN
F拉
O
O
F拉
F拉
F拉
V
V
V
O
实例一:绳拉小球,在光滑水平面上做匀速圆周运动
FN与G相平衡,合力为F拉
特点:合力F拉总指向圆心,且与v垂直
实例二:物体相对转盘静止,随转盘做匀速圆周运动
G
ω
O
FN
f静
实例二:物体相对转盘静止,随转盘做匀速圆周运动
O
f静
f静
f静
V
V
V
FN与G相平衡,合力为f静
特点:合力f静总指向圆心,且与v垂直
实例三:飞椅与人一起做匀速圆周运动
r
O'
O
θ
l
h
FT
G
F合
合力:重力与拉力的合力
实例三:飞椅与人一起做匀速圆周运动
特点:合力总指向圆心,且与v垂直
合力总指向圆心
整合归纳
合力f静总指向圆心
合力F拉总指向圆心
向心力为
重力与拉力的合力
向心力为f静
向心力为F拉
2、方向:
1、定义:
一、向心力
做匀速圆周运动的物体受到的合外力指向圆心,这个力叫做向心力。
总指向圆心,与速度垂直,方向不断变化。
3、向心力的作用效果:只改变速度的方向,不改变速度的大小。
那它是不是一种新力?
G
Ff
FN
ω
物块随着圆桶一起匀速转动时,物块的受力?物块向心力的来源
物块做匀速圆周运动时,合力提供向心力,即桶对物块的支持力。
匀速圆周运动实例分析——向心力的来源
总结:
向心力的来源:可以是重力、弹力、摩擦力等各种性质的力,也可以是几个力的合力,还可以是某个力的分力。
物体做匀速圆周运动时,由合力提供向心力。
向心力不是物体真实受到的一个力,不能说物体受到向心力的作用 ,只能说某个力或某几个力提供了向心力。
二、向心力的大小
例2. 小球做圆锥摆时细绳长L,与竖直方向成θ角,求小球做匀速圆周运动的向心力和角速度ω。
O’
O
mg
T
F
θ
L
小球做圆周运动的半径
由牛顿第二定律:
即:
R
解析:小球的向心力由T和G的合力提供
变式.如图所示,一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
A.球A的线速度一定大于球B的线速度
B.球A的角速度一定小于球B的角速度
C.球A的运动周期一定小于球B的运动周期
D.球A对筒壁的压力一定大于球B对筒壁的压力
mg
N
F
AB
v
1、做变速圆周运动的物体所受的合力特点:
F
Fn
Ft
Ft 切向分力,它产生切向加速度,改变速度的大小.
Fn 向心分力,它产生向心加速度,改变速度的方向.
加速
①F与V夹角为锐角时做加速圆周运动
②F与V夹角为直角时做匀速圆周运动
③F与V夹角为钝角时做减速圆周运动
把一般曲线分割为许多极短的小段,每一段都可以看作为一小段圆弧,而这些圆弧的弯曲程度不一样,表明它们具有不同的曲率半径。在注意到这点区别之后,分析质点经过曲线上某位置的运动时,就可以采用圆周运动的分析方法对一般曲线运动进行处理了。
r1
r2
2、处理一般曲线运动的方法:
匀速圆周运动:
非匀速圆周运动:
F向是F合的指向圆心方向的分力Fn
向心力的来源:可以是重力、弹力、摩擦力等各种性质的力,也可以是几个力的合力,还可以是某个力的分力。
物体做匀速圆周运动时,由合力提供向心力。
小结
例、一辆汽车在水平公路上转弯,沿曲线由M向N行驶,速度逐渐减小.如图所示,分别画出了汽车转弯时所受合力的四种方向,你认为正确的是( )
A B C D
1.如图所示,汽车在一水平公路上转弯时,汽车的运动可视为匀速圆周运动。下列关于汽车转弯时的说法正确的是( )
A.汽车处于平衡状态 B.汽车的向心力由重力和支持力提供
C.汽车的向心力由摩擦力提供 D.汽车的向心力由支持力提供
C
C
2.甲、乙两物体做匀速圆周运动,其质量之比为1:2,转动半径之比为1:2,在相等时间里甲转过60°,乙转过45°,则它们所受合外力之比为( )
A.1:4 B.2:3 C.4:9 D.9:16
C
