人教版九年级数学下册第29 章投影与视图单元复习测试题(word版含答案)
文档属性
| 名称 | 人教版九年级数学下册第29 章投影与视图单元复习测试题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 425.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 19:59:40 | ||
图片预览


文档简介
人教版九年级数学下册第29 章《投影与视图》
单元复习测试题(含答案)
测试时间:90分钟
第Ⅰ卷 [基础测试卷]
一、选择题(每小题2分,共20分)
1.平行投影中的光线是 ( )
A.平行的 B.聚成一点的 C.不平行的 D.向四面八方发散的
2.两个不同长度的物体在同一时刻同一地点的太阳光下得到的投影是 ( )
A.相等 B.长的较长 C.短的较长 D.不能确定
3.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下 ( )
A.小明的影子比小强的影子长 B.小明的影长比小强的影子短
C.小明的影子和小强的影子一样长 D.无法判断谁的影子长
4.木棒长为1.2 m,则它的正投影的长一定 ( )
A.大于1.2 m B.小于1.2 m C.等于1.2 m D.小于或等于1.2 m
5.小明从正面观察如图所示的两个物体,看到的是 ( )
6.在同一时刻太阳光下,身高1.6 m的小强的影长是1.2 m,旗杆的影长是15 m,则旗杆高为 ( )
A.16 m B.18 m C.20 m D.22 m
7.如图所示是一根电线杆在一天中不同时刻的影长图,试按一天中时间先后顺序排列,正确的是 ( )
A.①②③④ B.④①③② C.④②③① D.④③②①
8.某几何体的主视图、左视图和俯视图分别如图,则该几何体的体积为 ( )
A.π B.2π C.3π D.4π
9.小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为 ( )
A.上午8时 B.上午9时30分 C.上午10时 D.上午12时
10.棱长是1㎝的小立方体组成如图所示的几何体,那么这个几何体的表面积是 ( )
A.36 B.33
C.30 D.27
二、填空题(每小题2分,共20分)
1.太阳光线形成的投影是_________,手电筒、路灯、台灯的光线形成的投影称为_________.
2.平行于投影面的平行四边形的面积与它的正投影的面积的大小关系是 .
3.在①长方体、②球、③圆锥、④圆柱、⑤三棱柱这五种几何体中,其主视图、左视图、俯视图都完全相同的是 .(填序号)
4.小军晚上到广场去玩,他发现有两人的影子一个向东,一个向西,于是他肯定的说:“广场上的大灯泡一定位于两人 ”.
5.如图所示,水平放置的长方体的底面是边长为2和4的矩形,它的左视图的面积为6,则长方体的体积等于 .
6.为了测量水塔的高度,我们取一竹杆,放在阳光下,已知2米长的竹杆投影长为1.5米,在同一时刻测得水塔的投影长为30米,则水塔高为 米.
7.小芳的房间有一面积为3m2的玻璃窗,她站在室内离窗子4m的地方向外看,她能看到窗前面一幢楼房的面积有_________m2(楼之间的距离为20m).
8.如图所示是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是 .
9.如图所示,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭的几何体拼成一个大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小正方体,王亮所搭几何体表面积为_____________.
10.如图是一个几何体的三视图,根据图示的数据可以计算出该几何体的表面积为 .
三.画图题(每小题8分,共16分)
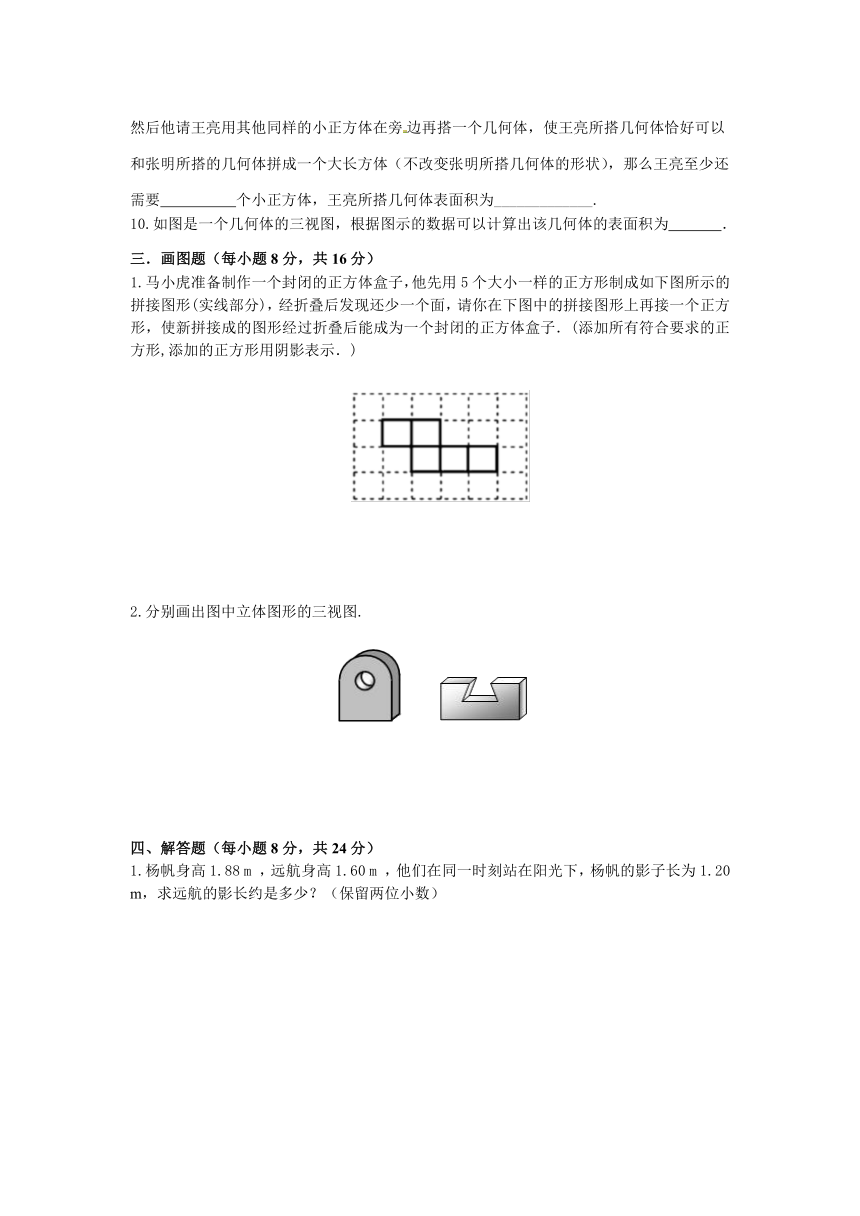
1.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如下图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在下图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(添加所有符合要求的正方形,添加的正方形用阴影表示.)
2.分别画出图中立体图形的三视图.
四、解答题(每小题8分,共24分)
1.杨帆身高1.88 m ,远航身高1.60 m ,他们在同一时刻站在阳光下,杨帆的影子长为1.20 m,求远航的影长约是多少?(保留两位小数)
2.确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.
3.已知,如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
五、解答题(每小题10分,共20分)
1.如图是一粮仓,其顶部是一圆锥,底部是一圆柱.
(1)画出粮仓的三视图;
(2)若圆柱的底面圆的半径为1 m,高为2 m,求圆柱的侧面积;
(3)假设粮食最多只能装到与圆柱同样高,则最多可以存放多少立方米的粮食?
2.如图所示为一几何体的三视图:
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种表面展开图;
(3)若长方形的高为10 cm,正三角形的边长为4cm,
求这个几何体的侧面积.
第Ⅱ卷 [实践操作卷]
一、试一试(10分)
有若干个大小相同的小立方块搭成的几何体图形如图1,请在下图的方框中画出它的三视图.
二、算一算(10分)
如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米.如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
参考答案
第Ⅰ卷
一、选择题:
1.A;2.D;3.D;4.D;5.C;6.C;7.B;8.C;9.A;10.C.
二、填空题:
1.平行投影,中心投影;2. 相等;3.②;4.中间的上方; 5.24;6.40;7.108;8.6;9.19,48;10.90π
三、画图题:
1.可从图中“●”任选一格:
2.图形如下图所示.
四、解答题:
1.远航的影长约为1.02米.
2.如下图所示:
3.(1)连接AC,过点D作DF//AC,交直线BC于点F,线段EF即为DE的投影;
(2)DE的长为10m.
五、解答题:
1.(1)粮仓的三视图如图所示:
(2)S圆柱侧=2π·1×2=4πm2
(3)V=π×12×2=2π(m3),即最多可存放2πm3的粮食
2.(1)正三棱柱;
(2)如图所示;
(3)10×4×3=120(cm2).
第Ⅱ卷
一、略.
二、路灯杆AB的高度约为6.0m
俯视图
左视图
主视图
小赵
D
C
第10题图
第9题图
第8题图
第5题图
单元复习测试题(含答案)
测试时间:90分钟
第Ⅰ卷 [基础测试卷]
一、选择题(每小题2分,共20分)
1.平行投影中的光线是 ( )
A.平行的 B.聚成一点的 C.不平行的 D.向四面八方发散的
2.两个不同长度的物体在同一时刻同一地点的太阳光下得到的投影是 ( )
A.相等 B.长的较长 C.短的较长 D.不能确定
3.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下 ( )
A.小明的影子比小强的影子长 B.小明的影长比小强的影子短
C.小明的影子和小强的影子一样长 D.无法判断谁的影子长
4.木棒长为1.2 m,则它的正投影的长一定 ( )
A.大于1.2 m B.小于1.2 m C.等于1.2 m D.小于或等于1.2 m
5.小明从正面观察如图所示的两个物体,看到的是 ( )
6.在同一时刻太阳光下,身高1.6 m的小强的影长是1.2 m,旗杆的影长是15 m,则旗杆高为 ( )
A.16 m B.18 m C.20 m D.22 m
7.如图所示是一根电线杆在一天中不同时刻的影长图,试按一天中时间先后顺序排列,正确的是 ( )
A.①②③④ B.④①③② C.④②③① D.④③②①
8.某几何体的主视图、左视图和俯视图分别如图,则该几何体的体积为 ( )
A.π B.2π C.3π D.4π
9.小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为 ( )
A.上午8时 B.上午9时30分 C.上午10时 D.上午12时
10.棱长是1㎝的小立方体组成如图所示的几何体,那么这个几何体的表面积是 ( )
A.36 B.33
C.30 D.27
二、填空题(每小题2分,共20分)
1.太阳光线形成的投影是_________,手电筒、路灯、台灯的光线形成的投影称为_________.
2.平行于投影面的平行四边形的面积与它的正投影的面积的大小关系是 .
3.在①长方体、②球、③圆锥、④圆柱、⑤三棱柱这五种几何体中,其主视图、左视图、俯视图都完全相同的是 .(填序号)
4.小军晚上到广场去玩,他发现有两人的影子一个向东,一个向西,于是他肯定的说:“广场上的大灯泡一定位于两人 ”.
5.如图所示,水平放置的长方体的底面是边长为2和4的矩形,它的左视图的面积为6,则长方体的体积等于 .
6.为了测量水塔的高度,我们取一竹杆,放在阳光下,已知2米长的竹杆投影长为1.5米,在同一时刻测得水塔的投影长为30米,则水塔高为 米.
7.小芳的房间有一面积为3m2的玻璃窗,她站在室内离窗子4m的地方向外看,她能看到窗前面一幢楼房的面积有_________m2(楼之间的距离为20m).
8.如图所示是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是 .
9.如图所示,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭的几何体拼成一个大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小正方体,王亮所搭几何体表面积为_____________.
10.如图是一个几何体的三视图,根据图示的数据可以计算出该几何体的表面积为 .
三.画图题(每小题8分,共16分)
1.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如下图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在下图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(添加所有符合要求的正方形,添加的正方形用阴影表示.)
2.分别画出图中立体图形的三视图.
四、解答题(每小题8分,共24分)
1.杨帆身高1.88 m ,远航身高1.60 m ,他们在同一时刻站在阳光下,杨帆的影子长为1.20 m,求远航的影长约是多少?(保留两位小数)
2.确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.
3.已知,如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
五、解答题(每小题10分,共20分)
1.如图是一粮仓,其顶部是一圆锥,底部是一圆柱.
(1)画出粮仓的三视图;
(2)若圆柱的底面圆的半径为1 m,高为2 m,求圆柱的侧面积;
(3)假设粮食最多只能装到与圆柱同样高,则最多可以存放多少立方米的粮食?
2.如图所示为一几何体的三视图:
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种表面展开图;
(3)若长方形的高为10 cm,正三角形的边长为4cm,
求这个几何体的侧面积.
第Ⅱ卷 [实践操作卷]
一、试一试(10分)
有若干个大小相同的小立方块搭成的几何体图形如图1,请在下图的方框中画出它的三视图.
二、算一算(10分)
如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米.如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
参考答案
第Ⅰ卷
一、选择题:
1.A;2.D;3.D;4.D;5.C;6.C;7.B;8.C;9.A;10.C.
二、填空题:
1.平行投影,中心投影;2. 相等;3.②;4.中间的上方; 5.24;6.40;7.108;8.6;9.19,48;10.90π
三、画图题:
1.可从图中“●”任选一格:
2.图形如下图所示.
四、解答题:
1.远航的影长约为1.02米.
2.如下图所示:
3.(1)连接AC,过点D作DF//AC,交直线BC于点F,线段EF即为DE的投影;
(2)DE的长为10m.
五、解答题:
1.(1)粮仓的三视图如图所示:
(2)S圆柱侧=2π·1×2=4πm2
(3)V=π×12×2=2π(m3),即最多可存放2πm3的粮食
2.(1)正三棱柱;
(2)如图所示;
(3)10×4×3=120(cm2).
第Ⅱ卷
一、略.
二、路灯杆AB的高度约为6.0m
俯视图
左视图
主视图
小赵
D
C
第10题图
第9题图
第8题图
第5题图
