2021-2022学年人教版八年级数学下册18.1平行四边形同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.1平行四边形同步练习题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 198.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教版八年级数学下册《18-1平行四边形》同步练习题(附答案)
一.选择题
1.四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD,从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.6种 B.5种 C.4种 D.3种
2.四边形ABCD中,对角线AC、BD相交于点O,下列条件能判定这个四边形是平行四边形的是( )
A.AB=CD,AD∥BC B.AB=BC,AD=CD
C.AO=CO,BO=DO D.AB=CD,∠ADC=∠ABC
3. ABCD中,CE平分∠BCD.若BC=10,AE=4,则 ABCD的周长是( )
A.28 B.32 C.36 D.40
4.下列说法不正确的是( )
A.两组对边分别平行的四边形是平行四边形
B.一组对边平行,另一组对边相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边平行,一组对角相等的四边形是平行四边形
二.填空题
5.如图,在 ABCD中,AC、BD相交于点O,AC=20cm,BD=32cm,若△ABO的周长等于40cm,则CD= cm.
6.在平面直角坐标系中,平行四边形OABC的顶点A、C的坐标分别是(6,1)、(2,4),则点B的坐标是 .
7.如图,在平面直角坐标系中, ABCD的顶点坐标分别为A(3,a)、B(2,2)、C(b,3)、D(8,6),则a+b的值为 .
8.如图,在 ABCD中,线段BE、CE分别平分∠ABC和∠BCD,若AB=5,BE=8,则CE的长度为 .
9.如图,在四边形ABCD中,AD∥BC,∠B=60°,∠C=30°,AD=1,AB=2,则BC的长为 .
10.如图,在 ABCD中,对角线AC、BD相交于点O且DB⊥BC,若AC=10cm,BD=6cm,则AD= cm.
11.如图,点E,F在平行四边形ABCD的对角线BD上,BE=DF,若平行四边形ABCD的面积是20cm2,△ABE的面积是3cm2,则平行四边形AECF的面积是 cm2.
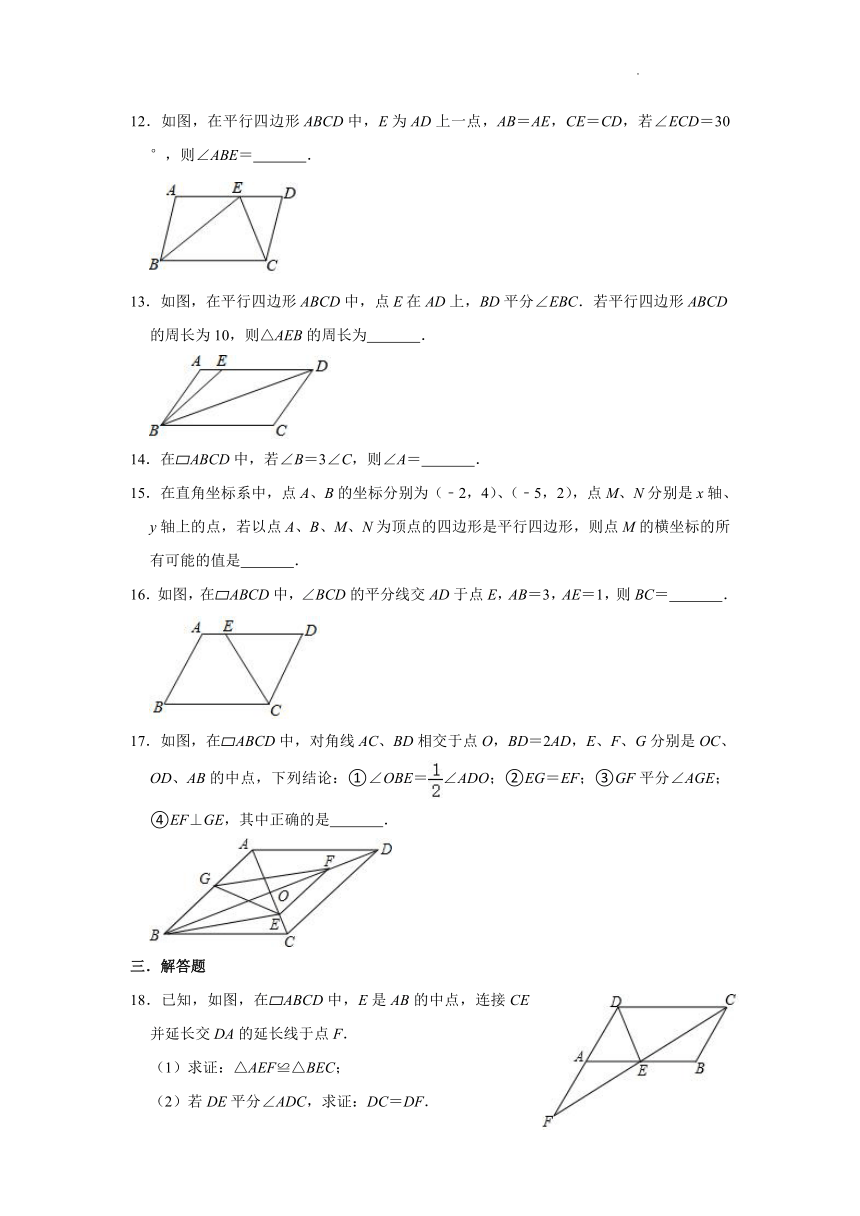
12.如图,在平行四边形ABCD中,E为AD上一点,AB=AE,CE=CD,若∠ECD=30°,则∠ABE= .
13.如图,在平行四边形ABCD中,点E在AD上,BD平分∠EBC.若平行四边形ABCD的周长为10,则△AEB的周长为 .
14.在 ABCD中,若∠B=3∠C,则∠A= .
15.在直角坐标系中,点A、B的坐标分别为(﹣2,4)、(﹣5,2),点M、N分别是x轴、y轴上的点,若以点A、B、M、N为顶点的四边形是平行四边形,则点M的横坐标的所有可能的值是 .
16.如图,在 ABCD中,∠BCD的平分线交AD于点E,AB=3,AE=1,则BC= .
17.如图,在 ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①∠OBE=∠ADO;②EG=EF;③GF平分∠AGE;④EF⊥GE,其中正确的是 .
三.解答题
18.已知,如图,在 ABCD中,E是AB的中点,连接CE并延长交DA的延长线于点F.
(1)求证:△AEF≌△BEC;
(2)若DE平分∠ADC,求证:DC=DF.
19.如图,线段AC与BD相交于点O,点O是AC的中点,AB=DC=AC.求证:四边形ABCD是平行四边形.
20.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F在BD上,且BE=DF,连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.
(1)求证:AE=CF;
(2)若AC平分∠HAG,判断四边形AGCH的形状,并证明你的结论.
21.如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.
求证:(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形.
参考答案
一.选择题
1.解:①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形;
①③可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
①④可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
∴有4种可能使四边形ABCD为平行四边形.
故选:C.
2.解:因为对角线互相平分的四边形是平行四边形,
故选:C.
3.解:∵四边形ABCD是平行四边形,
∴AD=BC=10,AB=DC,AD∥BC,
∴DE=AD﹣AE=6,∠DEC=∠BCE,
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∴∠DEC=∠DCE,
∴DC=DE=6,
∴ ABCD的周长=2(DC+BC)=2(6+10)=32;
故选:B.
4.解:A、∵两组对边分别平行的四边形是平行四边形,
∴选项A不符合题意;
B、∵一组对边平行,另一组对边相等的四边形不一定是平行四边形,
∴选项B符合题意;
C、∵一组对边平行且相等的四边形是平行四边形,
∴选项C不符合题意;
D、∵一组对边平行,一组对角相等的四边形是平行四边形,
∴选项D不符合题意;
故选:B.
二.填空题
5.解:∵四边形ABCD是平行四边形,
∴AO=CO=AC=10(cm),BO=DO=BD=16(cm),AB=CD,
∵△ABO的周长等于40cm,
∴AB+AO+BO=40(cm),
∴AB=40﹣10﹣16=14(cm),
∴CD=14(cm),
故答案为:14.
6.解:∵四边形OABC是平行四边形,
∴OA∥CB,且OA=CB,
∵点O的坐标为(0,0),点A的坐标为(6,1),
∴相当于将点O向右平移6个单位,向上平移1个单位,
∴点C(2,4)向右平移6个单位,向上平移1个单位为(8,5),
故答案为:(8,5).
7.解:如图,连接AC、BD交于点O′.
∵四边形ABCD是平行四边形,
∴AO′=O′C,BO′=O′D,
∵A(3,a),B(2,2),C(b,3),D(8,6),
∴,,
∴a=5,b=7,
∴a+b=12,
故答案为:12
8.解:∵BE和CE分别平分∠ABC和∠BCD,
∴∠ABE=∠EBC,∠DCE=∠ECB,
∵ ABCD,
∴AB∥CD,AB=CD=5,
∴∠ABC+∠DCB=180°,∠AEB=∠EBC,∠DEC=∠ECB,
∴(∠ABC+∠DCB)=90°,∠ABE=∠AEB,∠DEC=∠DCE,
∴∠EBC+∠ECB=90°,AB=AE=5,CD=DE=AB=5,
∴△EBC是直角三角形,AD=BC=AE+ED=10
根据勾股定理:CE=.
故答案为:6
9.解:作DE∥AB交BC于点E,则四边形ABED是平行四边形.
∴AB=DE=2,AD=BE=1,∠DEC=∠B=60°,
∵∠C=30°,
∴∠EDC=180°﹣60°﹣30°=90°.
∴EC=2DE=4.
∴BC=BE+EC=1+4=5.
故答案是:5.
10.解:∵四边形ABCD是平行四边形,AC=10cm,BD=6cm,
∴AD=BC,OC=AC=5cm,OB=BD=3cm,
∵DB⊥BC,
∴∠OBC=90°,
∴BC==4cm,
∴AD=4cm;
故答案为:4.
11.解:∵BE=DF,
∴S△ABE=S△ADF=3,
又∵平行四边形ABCD的面积是20cm2,
∴S△ABD=10cm2,
∴S△AEF=4cm2,
∴平行四边形AECF的面积是8cm2,
故答案为:8.
12.解:∵CE=CD,∠ECD=30°,
∴∠D=×(180°﹣30°)=75°,
∵四边形ABCD是平行四边形.
∴AB∥CD,
∴∠A+∠D=180°,
∴∠A=105°,
∵AB=AE,
∴∠ABE=×(180°﹣105°)=37.5°.
故答案为:37.5°.
13.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠EBC,
∴∠EBD=∠ADB,
∴∠EBD=∠ADB,
∴BE=DE,
∴△AEB的周长=AB+BE+AE=AB+DE+AE=AB+AD,
∵ ABCD的周长为10,
∴AB+AD=5,
∴△ABE的周长=AB+AD=5;
故答案为:5.
14.解:如图所示.
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠C+∠B=180°.
∵∠B=3∠C,
∴4∠C=180°.
∴∠A=∠C=45°.
故答案为:45°.
15.解:如图所示:
当AB平行且等于N1M1时,四边形ABM1N1是平行四边形;
当AB平行且等于N2M2时,四边形ABN2M2是平行四边形;
当AB为对角线时,四边形AN3BM3是平行四边形.
故符合题意的有3个点,点M的横坐标分别为﹣7,﹣3,3.
故答案为:﹣7,﹣3,3.
16.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=3,AD=BC,
∴∠DEC=∠BCE,
∵CE平分∠BCD,
∴∠BCE=∠ECD,
∴∠DEC=∠ECD,
∴DE=CD=3,
∴BC=AD=AE+DE=1+3=4;
故答案为:4.
17.解:①∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,DO=BO=BD,
∴∠ADB=∠DBC,
∵BD=2AD,
∴AD=DO,
∴BC=BO,
∵E是CO中点,
∴∠OBE=∠OBC,
∴∠OBE=∠ADO,故①正确;
②∵BC=BO,
∴△BOC是等腰三角形,
∵E是CO中点,
∴EB⊥CO,
∴∠BEA=90°,
∵G为AB中点,
∴EG=AB,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵E、F分别是OC、OD的中点,
∴EF=CD
∴EG=EF,故②正确;
③∵,E、F分别是OC、OD的中点,
∴EF∥DC,
∵DC∥AB,
∴EF∥AB,
∴∠EFG=∠AGF,
∵EF=EG,
∴∠EFG=∠EGF,
∴∠EGF=∠AGF,
∴GF平分∠AGE,故③正确;
④∵BC=BO,E是CO中点,
∴BE⊥AE,
由②、③得:EF∥AB,EF=CD=AB=BG,
∴四边形BEFG是平行四边形,
∵EG=EF,
∴要使EF⊥GE,则∠EFG=∠EBA=∠EAB=45°,
没有条件AE=BE,或∠BAC=45°,故④错误;
故答案为:①②③.
三.解答题
18.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠F=∠BCE,
∵E是AB中点,
∴AE=EB,
∵∠AEF=∠BEC,
∴△AEF≌△BEC.
(2)证明:∵DE平分∠ADC,
∴∠EDA=∠EDC,
∵AE∥CD,
∴∠CDE=∠AED,
∴∠EDA=∠AED,
∴AD=AE,
∵△AEF≌△BEC,
∴AF=BC=AD,
∴DF=2AD,DC=AB=2AE,
∴DC=DF.
19.证明:∵点O是AC的中点,
∴OA=OC,
∵AB=DC=AC,
∴AB=OA,CD=OC,
则∠ABO=∠AOB,∠CDO=∠COD,
又∠AOB=∠COD,
∴∠ABO=∠CDO,
即AB∥CD,
又∵AB=CD,
∴四边形ABCD是平行四边形.
20.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OB﹣BE=OD﹣DF,
即OE=OF,
又∵∠AOE=∠COF,
∴△AOE≌△COF(SAS),
∴AE=CF.
(2)四边形AGCH是菱形.理由如下:
∵△AOE≌△COF,
∴∠EAO=∠FCO,
∴AG∥CH,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴四边形AGCH是平行四边形,
∵AD∥BC,
∴∠HAC=∠ACB,
∵AC平分∠HAG,
∴∠HAC=∠GAC,
∵∠GAC=∠ACB,
∴GA=GC,
∴平行四边形AGCH是菱形.
21.证明:(1)如图,∵AD∥BC,DF∥BE,
∴∠1=∠2,∠3=∠4.
又AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在△AFD与△CEB中,
,
∴△AFD≌△CEB(ASA);
(2)由(1)知,△AFD≌△CEB,则AD=CB.
又∵AD∥BC,
∴四边形ABCD是平行四边形.
一.选择题
1.四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD,从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.6种 B.5种 C.4种 D.3种
2.四边形ABCD中,对角线AC、BD相交于点O,下列条件能判定这个四边形是平行四边形的是( )
A.AB=CD,AD∥BC B.AB=BC,AD=CD
C.AO=CO,BO=DO D.AB=CD,∠ADC=∠ABC
3. ABCD中,CE平分∠BCD.若BC=10,AE=4,则 ABCD的周长是( )
A.28 B.32 C.36 D.40
4.下列说法不正确的是( )
A.两组对边分别平行的四边形是平行四边形
B.一组对边平行,另一组对边相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边平行,一组对角相等的四边形是平行四边形
二.填空题
5.如图,在 ABCD中,AC、BD相交于点O,AC=20cm,BD=32cm,若△ABO的周长等于40cm,则CD= cm.
6.在平面直角坐标系中,平行四边形OABC的顶点A、C的坐标分别是(6,1)、(2,4),则点B的坐标是 .
7.如图,在平面直角坐标系中, ABCD的顶点坐标分别为A(3,a)、B(2,2)、C(b,3)、D(8,6),则a+b的值为 .
8.如图,在 ABCD中,线段BE、CE分别平分∠ABC和∠BCD,若AB=5,BE=8,则CE的长度为 .
9.如图,在四边形ABCD中,AD∥BC,∠B=60°,∠C=30°,AD=1,AB=2,则BC的长为 .
10.如图,在 ABCD中,对角线AC、BD相交于点O且DB⊥BC,若AC=10cm,BD=6cm,则AD= cm.
11.如图,点E,F在平行四边形ABCD的对角线BD上,BE=DF,若平行四边形ABCD的面积是20cm2,△ABE的面积是3cm2,则平行四边形AECF的面积是 cm2.
12.如图,在平行四边形ABCD中,E为AD上一点,AB=AE,CE=CD,若∠ECD=30°,则∠ABE= .
13.如图,在平行四边形ABCD中,点E在AD上,BD平分∠EBC.若平行四边形ABCD的周长为10,则△AEB的周长为 .
14.在 ABCD中,若∠B=3∠C,则∠A= .
15.在直角坐标系中,点A、B的坐标分别为(﹣2,4)、(﹣5,2),点M、N分别是x轴、y轴上的点,若以点A、B、M、N为顶点的四边形是平行四边形,则点M的横坐标的所有可能的值是 .
16.如图,在 ABCD中,∠BCD的平分线交AD于点E,AB=3,AE=1,则BC= .
17.如图,在 ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①∠OBE=∠ADO;②EG=EF;③GF平分∠AGE;④EF⊥GE,其中正确的是 .
三.解答题
18.已知,如图,在 ABCD中,E是AB的中点,连接CE并延长交DA的延长线于点F.
(1)求证:△AEF≌△BEC;
(2)若DE平分∠ADC,求证:DC=DF.
19.如图,线段AC与BD相交于点O,点O是AC的中点,AB=DC=AC.求证:四边形ABCD是平行四边形.
20.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F在BD上,且BE=DF,连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.
(1)求证:AE=CF;
(2)若AC平分∠HAG,判断四边形AGCH的形状,并证明你的结论.
21.如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.
求证:(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形.
参考答案
一.选择题
1.解:①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形;
①③可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
①④可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
∴有4种可能使四边形ABCD为平行四边形.
故选:C.
2.解:因为对角线互相平分的四边形是平行四边形,
故选:C.
3.解:∵四边形ABCD是平行四边形,
∴AD=BC=10,AB=DC,AD∥BC,
∴DE=AD﹣AE=6,∠DEC=∠BCE,
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∴∠DEC=∠DCE,
∴DC=DE=6,
∴ ABCD的周长=2(DC+BC)=2(6+10)=32;
故选:B.
4.解:A、∵两组对边分别平行的四边形是平行四边形,
∴选项A不符合题意;
B、∵一组对边平行,另一组对边相等的四边形不一定是平行四边形,
∴选项B符合题意;
C、∵一组对边平行且相等的四边形是平行四边形,
∴选项C不符合题意;
D、∵一组对边平行,一组对角相等的四边形是平行四边形,
∴选项D不符合题意;
故选:B.
二.填空题
5.解:∵四边形ABCD是平行四边形,
∴AO=CO=AC=10(cm),BO=DO=BD=16(cm),AB=CD,
∵△ABO的周长等于40cm,
∴AB+AO+BO=40(cm),
∴AB=40﹣10﹣16=14(cm),
∴CD=14(cm),
故答案为:14.
6.解:∵四边形OABC是平行四边形,
∴OA∥CB,且OA=CB,
∵点O的坐标为(0,0),点A的坐标为(6,1),
∴相当于将点O向右平移6个单位,向上平移1个单位,
∴点C(2,4)向右平移6个单位,向上平移1个单位为(8,5),
故答案为:(8,5).
7.解:如图,连接AC、BD交于点O′.
∵四边形ABCD是平行四边形,
∴AO′=O′C,BO′=O′D,
∵A(3,a),B(2,2),C(b,3),D(8,6),
∴,,
∴a=5,b=7,
∴a+b=12,
故答案为:12
8.解:∵BE和CE分别平分∠ABC和∠BCD,
∴∠ABE=∠EBC,∠DCE=∠ECB,
∵ ABCD,
∴AB∥CD,AB=CD=5,
∴∠ABC+∠DCB=180°,∠AEB=∠EBC,∠DEC=∠ECB,
∴(∠ABC+∠DCB)=90°,∠ABE=∠AEB,∠DEC=∠DCE,
∴∠EBC+∠ECB=90°,AB=AE=5,CD=DE=AB=5,
∴△EBC是直角三角形,AD=BC=AE+ED=10
根据勾股定理:CE=.
故答案为:6
9.解:作DE∥AB交BC于点E,则四边形ABED是平行四边形.
∴AB=DE=2,AD=BE=1,∠DEC=∠B=60°,
∵∠C=30°,
∴∠EDC=180°﹣60°﹣30°=90°.
∴EC=2DE=4.
∴BC=BE+EC=1+4=5.
故答案是:5.
10.解:∵四边形ABCD是平行四边形,AC=10cm,BD=6cm,
∴AD=BC,OC=AC=5cm,OB=BD=3cm,
∵DB⊥BC,
∴∠OBC=90°,
∴BC==4cm,
∴AD=4cm;
故答案为:4.
11.解:∵BE=DF,
∴S△ABE=S△ADF=3,
又∵平行四边形ABCD的面积是20cm2,
∴S△ABD=10cm2,
∴S△AEF=4cm2,
∴平行四边形AECF的面积是8cm2,
故答案为:8.
12.解:∵CE=CD,∠ECD=30°,
∴∠D=×(180°﹣30°)=75°,
∵四边形ABCD是平行四边形.
∴AB∥CD,
∴∠A+∠D=180°,
∴∠A=105°,
∵AB=AE,
∴∠ABE=×(180°﹣105°)=37.5°.
故答案为:37.5°.
13.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠EBC,
∴∠EBD=∠ADB,
∴∠EBD=∠ADB,
∴BE=DE,
∴△AEB的周长=AB+BE+AE=AB+DE+AE=AB+AD,
∵ ABCD的周长为10,
∴AB+AD=5,
∴△ABE的周长=AB+AD=5;
故答案为:5.
14.解:如图所示.
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠C+∠B=180°.
∵∠B=3∠C,
∴4∠C=180°.
∴∠A=∠C=45°.
故答案为:45°.
15.解:如图所示:
当AB平行且等于N1M1时,四边形ABM1N1是平行四边形;
当AB平行且等于N2M2时,四边形ABN2M2是平行四边形;
当AB为对角线时,四边形AN3BM3是平行四边形.
故符合题意的有3个点,点M的横坐标分别为﹣7,﹣3,3.
故答案为:﹣7,﹣3,3.
16.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=3,AD=BC,
∴∠DEC=∠BCE,
∵CE平分∠BCD,
∴∠BCE=∠ECD,
∴∠DEC=∠ECD,
∴DE=CD=3,
∴BC=AD=AE+DE=1+3=4;
故答案为:4.
17.解:①∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,DO=BO=BD,
∴∠ADB=∠DBC,
∵BD=2AD,
∴AD=DO,
∴BC=BO,
∵E是CO中点,
∴∠OBE=∠OBC,
∴∠OBE=∠ADO,故①正确;
②∵BC=BO,
∴△BOC是等腰三角形,
∵E是CO中点,
∴EB⊥CO,
∴∠BEA=90°,
∵G为AB中点,
∴EG=AB,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵E、F分别是OC、OD的中点,
∴EF=CD
∴EG=EF,故②正确;
③∵,E、F分别是OC、OD的中点,
∴EF∥DC,
∵DC∥AB,
∴EF∥AB,
∴∠EFG=∠AGF,
∵EF=EG,
∴∠EFG=∠EGF,
∴∠EGF=∠AGF,
∴GF平分∠AGE,故③正确;
④∵BC=BO,E是CO中点,
∴BE⊥AE,
由②、③得:EF∥AB,EF=CD=AB=BG,
∴四边形BEFG是平行四边形,
∵EG=EF,
∴要使EF⊥GE,则∠EFG=∠EBA=∠EAB=45°,
没有条件AE=BE,或∠BAC=45°,故④错误;
故答案为:①②③.
三.解答题
18.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠F=∠BCE,
∵E是AB中点,
∴AE=EB,
∵∠AEF=∠BEC,
∴△AEF≌△BEC.
(2)证明:∵DE平分∠ADC,
∴∠EDA=∠EDC,
∵AE∥CD,
∴∠CDE=∠AED,
∴∠EDA=∠AED,
∴AD=AE,
∵△AEF≌△BEC,
∴AF=BC=AD,
∴DF=2AD,DC=AB=2AE,
∴DC=DF.
19.证明:∵点O是AC的中点,
∴OA=OC,
∵AB=DC=AC,
∴AB=OA,CD=OC,
则∠ABO=∠AOB,∠CDO=∠COD,
又∠AOB=∠COD,
∴∠ABO=∠CDO,
即AB∥CD,
又∵AB=CD,
∴四边形ABCD是平行四边形.
20.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OB﹣BE=OD﹣DF,
即OE=OF,
又∵∠AOE=∠COF,
∴△AOE≌△COF(SAS),
∴AE=CF.
(2)四边形AGCH是菱形.理由如下:
∵△AOE≌△COF,
∴∠EAO=∠FCO,
∴AG∥CH,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴四边形AGCH是平行四边形,
∵AD∥BC,
∴∠HAC=∠ACB,
∵AC平分∠HAG,
∴∠HAC=∠GAC,
∵∠GAC=∠ACB,
∴GA=GC,
∴平行四边形AGCH是菱形.
21.证明:(1)如图,∵AD∥BC,DF∥BE,
∴∠1=∠2,∠3=∠4.
又AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在△AFD与△CEB中,
,
∴△AFD≌△CEB(ASA);
(2)由(1)知,△AFD≌△CEB,则AD=CB.
又∵AD∥BC,
∴四边形ABCD是平行四边形.
