2021-2022学年苏科版八年级数学下册9.3平行四边形解答题专题训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学下册9.3平行四边形解答题专题训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 468.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 20:09:23 | ||
图片预览


文档简介
2021-2022学年苏科版八年级数学下册《9-3平行四边形》解答题专题训练(附答案)
1.如图,在 ABCD中,延长AD到点E,延长CB到点F,使得DE=BF,连接EF,分别交CD,AB于点G,H,连接AG,CH.
求证:四边形AGCH是平行四边形.
2.如图,在平行四边形ABCD中,点E,F分别是边AD,BC的中点.
(1)求证:AF=CE;
(2)若四边形AECF的周长为10,AF=3,AB=2,求平行四边形ABCD的周长.
3.若平面内两点P1(x1,y1),P2(x2,y2),其两点间的距离P1P2=
.例如:已知A(3,1),B(5,2),则这两点间的距离
AB=.已知A(3,1),B(5,2),C(4,4).
(1)聪明的你能判定△ABC的形状吗?并说明理由.
(2)若以点A、B、C、D为顶点的四边形是平行四边形时,请直接写出点D的坐标.
4.已知:如图,在 ABCD中,E,F分别为BC和AD上的点,BD和EF相交于点O,且OE=OF.求证:四边形AECF为平行四边形.
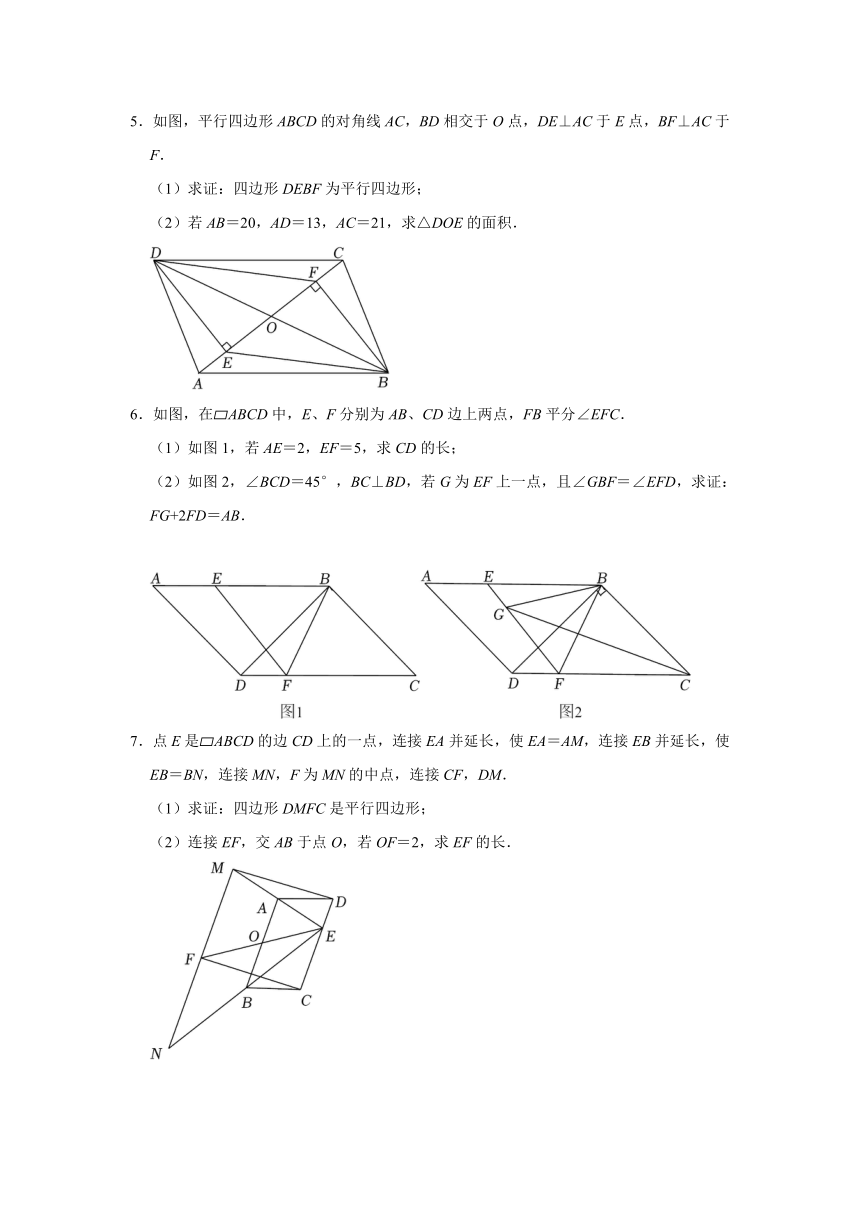
5.如图,平行四边形ABCD的对角线AC,BD相交于O点,DE⊥AC于E点,BF⊥AC于F.
(1)求证:四边形DEBF为平行四边形;
(2)若AB=20,AD=13,AC=21,求△DOE的面积.
6.如图,在 ABCD中,E、F分别为AB、CD边上两点,FB平分∠EFC.
(1)如图1,若AE=2,EF=5,求CD的长;
(2)如图2,∠BCD=45°,BC⊥BD,若G为EF上一点,且∠GBF=∠EFD,求证:FG+2FD=AB.
7.点E是 ABCD的边CD上的一点,连接EA并延长,使EA=AM,连接EB并延长,使EB=BN,连接MN,F为MN的中点,连接CF,DM.
(1)求证:四边形DMFC是平行四边形;
(2)连接EF,交AB于点O,若OF=2,求EF的长.
8.如图,在四边形ABCD中,AD∥BC,对角线AC、BD交于点O,且AO=OC,过点O作EF⊥BD,交AD于点E,交BC于点F.
(1)求证:四边形ABCD为平行四边形;
(2)连接BE,若∠BAD=100°,∠DBF=2∠ABE,求∠ABE的度数.
9.如图,在 ABCD中,BE∥DF且分别交对角线AC于点E、F,连接ED、BF.
求证:(1)四边形BEDF是平行四边形;
(2)若DF⊥AC,DF=12,DC=BF=13,求BC的长.
10.如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)求证:四边形AECD是平行四边形;
(2)若AB=BC,CD=5,AC=8,求四边形AECD的面积.
11.如图,在 ABCD中,点E在边BC上,点F在边AD的延长线上,且∠ADB=∠F,EF与CD交于点G.
(1)求证:四边形BDFE是平行四边形;
(2)若AD=10,BE=4,FG=5,求EG的长.
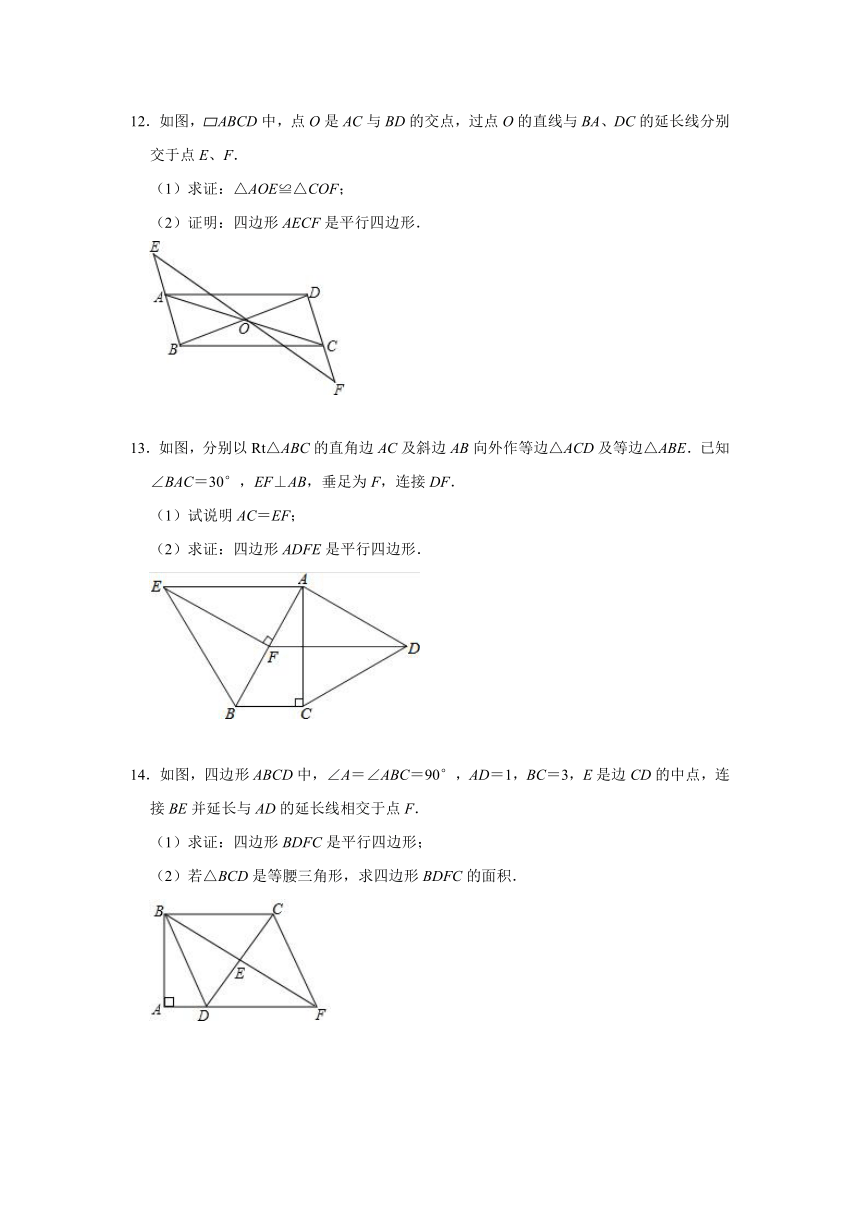
12.如图, ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F.
(1)求证:△AOE≌△COF;
(2)证明:四边形AECF是平行四边形.
13.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
14.如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
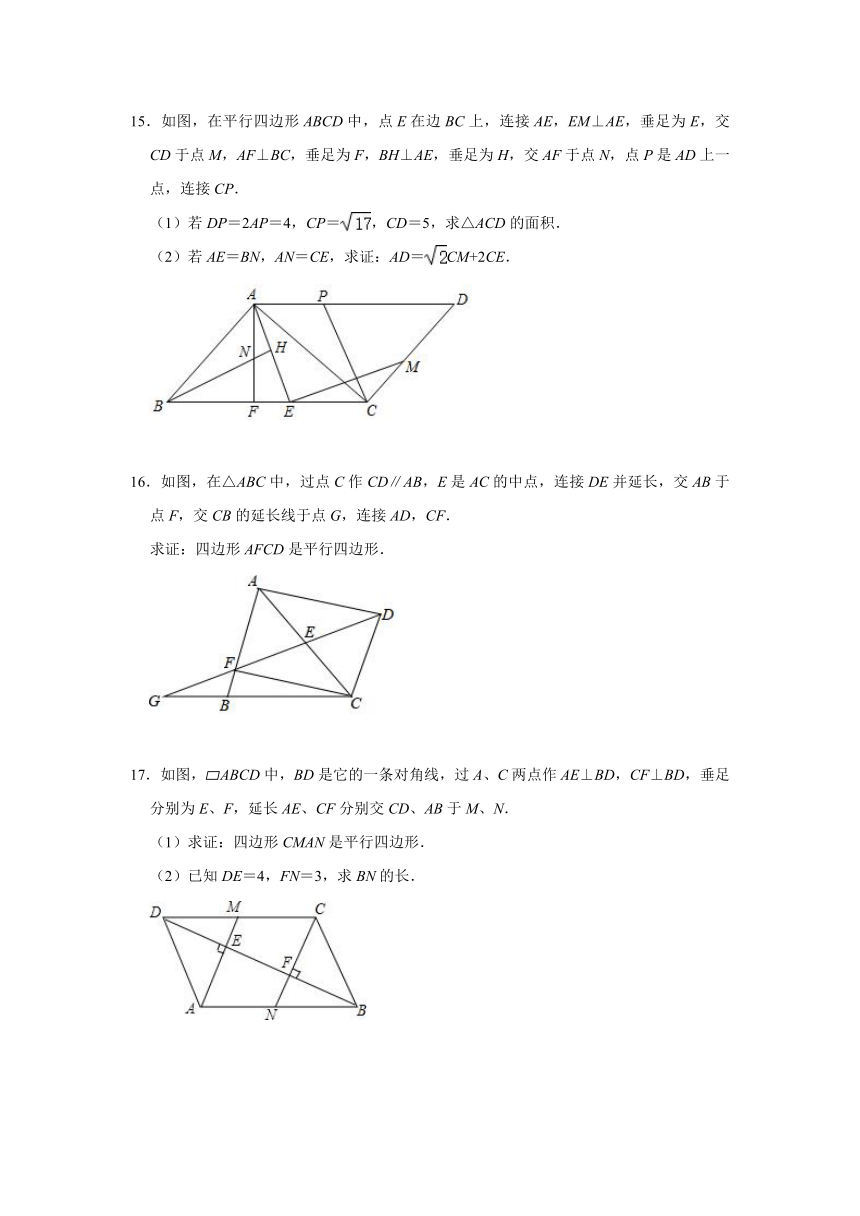
15.如图,在平行四边形ABCD中,点E在边BC上,连接AE,EM⊥AE,垂足为E,交CD于点M,AF⊥BC,垂足为F,BH⊥AE,垂足为H,交AF于点N,点P是AD上一点,连接CP.
(1)若DP=2AP=4,CP=,CD=5,求△ACD的面积.
(2)若AE=BN,AN=CE,求证:AD=CM+2CE.
16.如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G,连接AD,CF.
求证:四边形AFCD是平行四边形.
17.如图, ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.
(1)求证:四边形CMAN是平行四边形.
(2)已知DE=4,FN=3,求BN的长.
18.如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
19.如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠F=45°,BD=2,求AC的长.
20.如图所示,在 ABCD中,点E,F在对角线BD上,且BE=DF,求证:
(1)AE=CF;
(2)四边形AECF是平行四边形.
参考答案
1.证明:∵四边形ABCD是平行四边形,
∴∠EAH=∠FCG,AD∥BC,AD=BC,
∴∠E=∠F,
∵AD=BC,DE=BF,
∴AD+DE=BC+BF,
即AE=CF,
在△AEH与△CFG中,
,
∴△AEH≌△CFG(ASA),
∴A=CG,
∵AH∥CG,
∴四边形AGCH是平行四边形.
2.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,即AE∥CF,
又∵点E,F分别是边AD,BC的中点,
∴AE=AD,CF=BC,
∴AE=CF,
∴四边形AECF为平行四边形,
∴AF=CE;
(2)解:∵四边形AECF的周长为10,AF=3,
∴AE+CF=10﹣2×3=4,
∵点E,F分别是边AD,BC的中点,
∴AD+BC=2(AE+CF)=8,
∵AB=2,
∴平行四边形ABCD的周长=8+2×2=12.
3.解:(1)能判定△ABC的形状,△ABC是等腰直角三角形;理由如下:
由题意得:AB=,BC==,AC==,
∴AB=BC,AB2+BC2=AC2,
∴△ABC是等腰直角三角形;
(2)如图所示:
当AB为对角线时,AD∥BC,
∵A(3,1),B(5,2),C(4,4),
∴把点B向下平移3个单位,再向左平移1个单位,得到点D,
∴点D的坐标为(4,﹣1);
当BC为对角线时,AB∥CD,
∵A(3,1),B(5,2),C(4,4),
∴把点B向上平移3个单位,再向右平移1个单位,得到点D',
∴点D'的坐标为(6,5);
当AC为对角线时,AD∥BC,
∵A(3,1),B(5,2),C(4,4),
∴把点A向上平移2个单位,再向左平移1个单位,得到点D'',
∴点D''的坐标为(2,3);
综上所述,点D的坐标为(4,﹣1)或(6,5)或(2,3).
4.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ODF=∠OBE,
在△DOF和△BOE中,
,
∴△DOF≌△BOE(AAS),
∴DF=BE,
∴AD﹣DF=BC﹣BE,
即AF=EC,
∴四边形AECF为平行四边形.
5.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BCF,
∵DE⊥AC于E点,BF⊥AC于F,
∴∠DEA=∠BFC=90°,
在△DEA与△BFC中,
,
∴△DEA≌△BFC(AAS),
∴DE=BF,
∵∠DEA=∠BFC=90°,
∴∠DEO=∠BFO=90°,
∴DE∥BF,
∴四边形DEBF是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AB=DC=20,AO=OC=10.5,
∵DE⊥AC,
在Rt△ADE中,AD2﹣AE2=DE2,
在Rt△DEC中,DC2﹣EC2=DE2,
即132﹣AE2=202﹣(21﹣AE)2,
解得:AE=5,
∴OE=OA﹣AE=10.5﹣5=5.5,DE=12,
∴△DOE的面积=.
6.(1)解:在 ABCD中,AB∥CD,AB=CD,
∴∠ABF=∠BFC,
∵FB平分∠EFC,
∴∠EFB=∠BFC,
∴∠ABF=∠EFB,
∵AE=2,EF=5,
∴BE=EF=5,
∴CD=AB=AE+EF=2+5=7;
(2)证明:在FC上截取FH=FG,连接BH,
在△BGF和△BHF中,
,
∴△BGF≌△BHF(SAS),
∴∠BGF=∠BHF,
∵∠GBF=∠EFD,
∵∠EFD+∠EFB+∠BFH=180°,∠EFB+∠BGF+∠GBF=180°,
∴∠BFH=∠BGF,
∴∠BFH=∠BHF,
∴∠BFD=∠BHC,
∵∠BCD=45°,BC⊥BD,
∴∠BDF=45°=∠BCH,
∴BD=BC,
在△BDF和△BCH中,
,
∴△BDF≌△BCH(AAS)
∴DF=CH,
∴AB=CD=DF+FH+CH=FG+2FD,
即FG+2FD=AB.
7.(1)证明:∵AE=AM,EB=BN,
∴AB为△EMN的中位线,
∴AB∥MN,AB=MN,
∵MF=MN,
∴AB∥MF,AB=MF,
∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴MF∥CD,MF=CD,
∴四边形MFCD为平行四边形;
(2)解:连接AF,BF,则AF是△MNE的中位线,
∴AF∥EB,AF=EB,
∴四边形AFBE是平行四边形,
∴OF=OE=2,
∴EF=4.
8.(1)证明:∵AD∥BC,
∴∠OAD=∠OCB,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴AD=CB,
又∵AD∥BC,
∴四边形ABCD为平行四边形;
(2)解:设∠ABE=x,则∠DBF=2x,
由(1)得:四边形ABCD为平行四边形,
∴OB=OD,
∵EF⊥BD,
∴BE=DE,
∴∠EBD=∠EDB,
∵AD∥BC,
∴∠EDB=∠DBF,
∴∠EBD=∠EDB=∠DBF=2x,
∵∠BAD+∠ABE+∠EBD+∠EDB=180°,
∴100°+x+2x+2x=180°,
解得:x=16°,
即∠ABE=16°.
9.(1)证明:∵在平行四边形ABCD中AB=CD,AB∥CD,
∴∠BAC=∠DCA,
又∵BE∥DF,
∴∠BEF=∠DFE,
∴∠BAE=∠CFD,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∵BE∥DF,
∴四边形BEDF是平行四边形;
(2)解:∵DF⊥AC,BE∥DF,
∴∠BEF=∠DFE=90°,
∴∠DFC=90°,
∵DF=12,DC=BF=13,
∴CF==5,
∵BE=DF=12,
∴EF==5,
∴CE=EF+CF=10,
∴BC===2.
故BC的长为2.
10.(1)证明:在△AOE和△COD中,
,
∴△AOE≌△COD(ASA),
∴OD=OE,
又∵AO=CO,
∴四边形AECD是平行四边形;
(2)解:∵AB=BC,AO=CO,
∴OB⊥AC,
∴平行四边形AECD是菱形,
∵AC=8,
∴CO=AC=4,
在Rt△COD中,由勾股定理得:OD===3,
∴DE=2OD=6,
∴菱形AECD的面积=AC×DE=×8×6=24.
11.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠ADB=∠F,
∴BD∥EF,
∴四边形BDFE是平行四边形;
(2)解:由(1)得:四边形BDFE是平行四边形,
∴DF=BE=4,
∵四边形ABCD是平行四边形,
∴BC=AD=10,
∴CE=BC﹣BE=10﹣4=6,AD∥BC,
∴EG=,
即EG的长为.
12.解:(1)∵四边形ABCD是平行四边形,
∴AO=OC,AB∥CD.
∴∠E=∠F.
∵在△AOE与△COF中,
,
∴△AOE≌△COF(AAS);
(2)如图,连接EC、AF,
由(1)可知△AOE≌△COF,
∴OE=OF,
∵AO=CO,
∴四边形AECF是平行四边形.
13.证明:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF
∴AF=BC,
在Rt△AFE和Rt△BCA中,
,
∴△AFE≌△BCA(HL),
∴AC=EF;
(2)∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形.
14.(1)证明:∵∠A=∠ABC=90°,
∴BC∥AD,
∴∠CBE=∠DFE,
在△BEC与△FED中,
,
∴△BEC≌△FED,
∴BE=FE,
又∵E是边CD的中点,
∴CE=DE,
∴四边形BDFC是平行四边形;
(2)①BC=BD=3时,由勾股定理得,AB===2,
所以,四边形BDFC的面积=3×2=6;
②BC=CD=3时,过点C作CG⊥AF于G,则四边形AGCB是矩形,
所以,AG=BC=3,
所以,DG=AG﹣AD=3﹣1=2,
由勾股定理得,CG===,
所以,四边形BDFC的面积=3×=3;
③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾,此时不成立;
综上所述,四边形BDFC的面积是6或3.
15.(1)解:作CG⊥AD于G,如图1所示:
设PG=x,则DG=4﹣x,
在Rt△PGC中,GC2=CP2﹣PG2=17﹣x2,
在Rt△DGC中,GC2=CD2﹣GD2=52﹣(4﹣x)2=9+8x﹣x2,
∴17﹣x2=9+8x﹣x2,
解得:x=1,即PG=1,
∴GC=4,
∵DP=2AP=4,
∴AD=6,
∴S△ACD=×AD×CG=×6×4=12;
(2)证明:连接NE,如图2所示:
∵BH⊥AE,AF⊥BC,AE⊥EM,
∴∠AEB+∠NBF=∠AEB+∠EAF=∠AEB+∠MEC=90°,
∴∠NBF=∠EAF=∠MEC,
在△NBF和△EAF中,,
∴△NBF≌△EAF(AAS),
∴BF=AF,NF=EF,
∴∠ABC=45°,∠ENF=45°,
∵∠ANB=90°+∠EAF,∠CEA=90°+∠MEC,
∴∠ANB=∠CEA,
在△ANB和△CEA中,,
∴△ANB≌△CEA(SAS),
∴∠CAE=∠ABN,
∵∠NBF=∠EAF,
∴∠ABF=∠FAC=45°
∴FC=AF=BF,
∴∠ANE=∠BCD=135°,AD=BC=2AF,
在△ANE和△ECM中,,
∴△ANE≌△ECM(ASA),
∴CM=NE,
又∵NF=NE=MC,
∴AF=MC+EC,
∴AD=MC+2EC.
16.解:(1)∵E是AC的中点,
∴AE=CE,
∵AB∥CD,
∴∠AFE=∠CDE,
在△AEF和△CED中,
∵,
∴△AEF≌△CED(AAS),
∴AF=CD,
又AB∥CD,即AF∥CD,
∴四边形AFCD是平行四边形;
17.(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,
∵AM⊥BD,CN⊥BD,
∴AM∥CN,
∴CM∥AN,AM∥CN,
∴四边形AMCN是平行四边形.
(2)∵四边形AMCN是平行四边形,
∴CM=AN,
∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴DM=BN,∠MDE=∠NBF,
在△MDE和△NBF中,
,
∴△MDE≌△NBF(AAS),
∴ME=NF=3,
在Rt△DME中,∵∠DEM=90°,DE=4,ME=3,
∴DM===5,
∴BN=DM=5.
18.证明:(1)∵△ABC是等边三角形,
∴∠ABC=60°,
∵∠EFB=60°,
∴∠ABC=∠EFB,
∴EF∥DC(内错角相等,两直线平行),
∵DC=EF,
∴四边形EFCD是平行四边形;
(2)连接BE
∵BF=EF,∠EFB=60°,
∴△EFB是等边三角形,
∴EB=EF,∠EBF=60°
∵DC=EF,
∴EB=DC,
∵△ABC是等边三角形,
∴∠ACB=60°,AB=AC,
∴∠EBF=∠ACB,
∴△AEB≌△ADC,
∴AE=AD.
19.(1)证明:∵AC⊥BD,∠FCA=90°,∠CBF=∠DCB.
∴BD∥CF,CD∥BF,
∴四边形DBFC是平行四边形;
(2)解:∵四边形DBFC是平行四边形,
∴CF=BD=2,
∵AB=BC,AC⊥BD,
∴AE=CE,
作CM⊥BF于M,
∵BC平分∠DBF,
∴CE=CM,
∵∠F=45°,
∴△CFM是等腰直角三角形,
∴CM=CF=,
∴AE=CE=,
∴AC=2.
20.证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF.
在△ABE和△CDF中,,
∴△ABE≌△CDF(SAS),
∴AE=CF.
(2)证法1:∵△ABE≌△CDF,
∴∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,
∴四边形AECF是平行四边形.
证法2:如图,连接AC,与BD相交于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
又∵BE=DF,∴OB﹣BE=OD﹣DF,
∴OE=OF.
∴四边形AECF是平行四边形(对角线互相平分的四边形是平行四边形)
1.如图,在 ABCD中,延长AD到点E,延长CB到点F,使得DE=BF,连接EF,分别交CD,AB于点G,H,连接AG,CH.
求证:四边形AGCH是平行四边形.
2.如图,在平行四边形ABCD中,点E,F分别是边AD,BC的中点.
(1)求证:AF=CE;
(2)若四边形AECF的周长为10,AF=3,AB=2,求平行四边形ABCD的周长.
3.若平面内两点P1(x1,y1),P2(x2,y2),其两点间的距离P1P2=
.例如:已知A(3,1),B(5,2),则这两点间的距离
AB=.已知A(3,1),B(5,2),C(4,4).
(1)聪明的你能判定△ABC的形状吗?并说明理由.
(2)若以点A、B、C、D为顶点的四边形是平行四边形时,请直接写出点D的坐标.
4.已知:如图,在 ABCD中,E,F分别为BC和AD上的点,BD和EF相交于点O,且OE=OF.求证:四边形AECF为平行四边形.
5.如图,平行四边形ABCD的对角线AC,BD相交于O点,DE⊥AC于E点,BF⊥AC于F.
(1)求证:四边形DEBF为平行四边形;
(2)若AB=20,AD=13,AC=21,求△DOE的面积.
6.如图,在 ABCD中,E、F分别为AB、CD边上两点,FB平分∠EFC.
(1)如图1,若AE=2,EF=5,求CD的长;
(2)如图2,∠BCD=45°,BC⊥BD,若G为EF上一点,且∠GBF=∠EFD,求证:FG+2FD=AB.
7.点E是 ABCD的边CD上的一点,连接EA并延长,使EA=AM,连接EB并延长,使EB=BN,连接MN,F为MN的中点,连接CF,DM.
(1)求证:四边形DMFC是平行四边形;
(2)连接EF,交AB于点O,若OF=2,求EF的长.
8.如图,在四边形ABCD中,AD∥BC,对角线AC、BD交于点O,且AO=OC,过点O作EF⊥BD,交AD于点E,交BC于点F.
(1)求证:四边形ABCD为平行四边形;
(2)连接BE,若∠BAD=100°,∠DBF=2∠ABE,求∠ABE的度数.
9.如图,在 ABCD中,BE∥DF且分别交对角线AC于点E、F,连接ED、BF.
求证:(1)四边形BEDF是平行四边形;
(2)若DF⊥AC,DF=12,DC=BF=13,求BC的长.
10.如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)求证:四边形AECD是平行四边形;
(2)若AB=BC,CD=5,AC=8,求四边形AECD的面积.
11.如图,在 ABCD中,点E在边BC上,点F在边AD的延长线上,且∠ADB=∠F,EF与CD交于点G.
(1)求证:四边形BDFE是平行四边形;
(2)若AD=10,BE=4,FG=5,求EG的长.
12.如图, ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F.
(1)求证:△AOE≌△COF;
(2)证明:四边形AECF是平行四边形.
13.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
14.如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
15.如图,在平行四边形ABCD中,点E在边BC上,连接AE,EM⊥AE,垂足为E,交CD于点M,AF⊥BC,垂足为F,BH⊥AE,垂足为H,交AF于点N,点P是AD上一点,连接CP.
(1)若DP=2AP=4,CP=,CD=5,求△ACD的面积.
(2)若AE=BN,AN=CE,求证:AD=CM+2CE.
16.如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G,连接AD,CF.
求证:四边形AFCD是平行四边形.
17.如图, ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.
(1)求证:四边形CMAN是平行四边形.
(2)已知DE=4,FN=3,求BN的长.
18.如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
19.如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠F=45°,BD=2,求AC的长.
20.如图所示,在 ABCD中,点E,F在对角线BD上,且BE=DF,求证:
(1)AE=CF;
(2)四边形AECF是平行四边形.
参考答案
1.证明:∵四边形ABCD是平行四边形,
∴∠EAH=∠FCG,AD∥BC,AD=BC,
∴∠E=∠F,
∵AD=BC,DE=BF,
∴AD+DE=BC+BF,
即AE=CF,
在△AEH与△CFG中,
,
∴△AEH≌△CFG(ASA),
∴A=CG,
∵AH∥CG,
∴四边形AGCH是平行四边形.
2.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,即AE∥CF,
又∵点E,F分别是边AD,BC的中点,
∴AE=AD,CF=BC,
∴AE=CF,
∴四边形AECF为平行四边形,
∴AF=CE;
(2)解:∵四边形AECF的周长为10,AF=3,
∴AE+CF=10﹣2×3=4,
∵点E,F分别是边AD,BC的中点,
∴AD+BC=2(AE+CF)=8,
∵AB=2,
∴平行四边形ABCD的周长=8+2×2=12.
3.解:(1)能判定△ABC的形状,△ABC是等腰直角三角形;理由如下:
由题意得:AB=,BC==,AC==,
∴AB=BC,AB2+BC2=AC2,
∴△ABC是等腰直角三角形;
(2)如图所示:
当AB为对角线时,AD∥BC,
∵A(3,1),B(5,2),C(4,4),
∴把点B向下平移3个单位,再向左平移1个单位,得到点D,
∴点D的坐标为(4,﹣1);
当BC为对角线时,AB∥CD,
∵A(3,1),B(5,2),C(4,4),
∴把点B向上平移3个单位,再向右平移1个单位,得到点D',
∴点D'的坐标为(6,5);
当AC为对角线时,AD∥BC,
∵A(3,1),B(5,2),C(4,4),
∴把点A向上平移2个单位,再向左平移1个单位,得到点D'',
∴点D''的坐标为(2,3);
综上所述,点D的坐标为(4,﹣1)或(6,5)或(2,3).
4.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ODF=∠OBE,
在△DOF和△BOE中,
,
∴△DOF≌△BOE(AAS),
∴DF=BE,
∴AD﹣DF=BC﹣BE,
即AF=EC,
∴四边形AECF为平行四边形.
5.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BCF,
∵DE⊥AC于E点,BF⊥AC于F,
∴∠DEA=∠BFC=90°,
在△DEA与△BFC中,
,
∴△DEA≌△BFC(AAS),
∴DE=BF,
∵∠DEA=∠BFC=90°,
∴∠DEO=∠BFO=90°,
∴DE∥BF,
∴四边形DEBF是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AB=DC=20,AO=OC=10.5,
∵DE⊥AC,
在Rt△ADE中,AD2﹣AE2=DE2,
在Rt△DEC中,DC2﹣EC2=DE2,
即132﹣AE2=202﹣(21﹣AE)2,
解得:AE=5,
∴OE=OA﹣AE=10.5﹣5=5.5,DE=12,
∴△DOE的面积=.
6.(1)解:在 ABCD中,AB∥CD,AB=CD,
∴∠ABF=∠BFC,
∵FB平分∠EFC,
∴∠EFB=∠BFC,
∴∠ABF=∠EFB,
∵AE=2,EF=5,
∴BE=EF=5,
∴CD=AB=AE+EF=2+5=7;
(2)证明:在FC上截取FH=FG,连接BH,
在△BGF和△BHF中,
,
∴△BGF≌△BHF(SAS),
∴∠BGF=∠BHF,
∵∠GBF=∠EFD,
∵∠EFD+∠EFB+∠BFH=180°,∠EFB+∠BGF+∠GBF=180°,
∴∠BFH=∠BGF,
∴∠BFH=∠BHF,
∴∠BFD=∠BHC,
∵∠BCD=45°,BC⊥BD,
∴∠BDF=45°=∠BCH,
∴BD=BC,
在△BDF和△BCH中,
,
∴△BDF≌△BCH(AAS)
∴DF=CH,
∴AB=CD=DF+FH+CH=FG+2FD,
即FG+2FD=AB.
7.(1)证明:∵AE=AM,EB=BN,
∴AB为△EMN的中位线,
∴AB∥MN,AB=MN,
∵MF=MN,
∴AB∥MF,AB=MF,
∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴MF∥CD,MF=CD,
∴四边形MFCD为平行四边形;
(2)解:连接AF,BF,则AF是△MNE的中位线,
∴AF∥EB,AF=EB,
∴四边形AFBE是平行四边形,
∴OF=OE=2,
∴EF=4.
8.(1)证明:∵AD∥BC,
∴∠OAD=∠OCB,
在△AOD和△COB中,
,
∴△AOD≌△COB(ASA),
∴AD=CB,
又∵AD∥BC,
∴四边形ABCD为平行四边形;
(2)解:设∠ABE=x,则∠DBF=2x,
由(1)得:四边形ABCD为平行四边形,
∴OB=OD,
∵EF⊥BD,
∴BE=DE,
∴∠EBD=∠EDB,
∵AD∥BC,
∴∠EDB=∠DBF,
∴∠EBD=∠EDB=∠DBF=2x,
∵∠BAD+∠ABE+∠EBD+∠EDB=180°,
∴100°+x+2x+2x=180°,
解得:x=16°,
即∠ABE=16°.
9.(1)证明:∵在平行四边形ABCD中AB=CD,AB∥CD,
∴∠BAC=∠DCA,
又∵BE∥DF,
∴∠BEF=∠DFE,
∴∠BAE=∠CFD,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∵BE∥DF,
∴四边形BEDF是平行四边形;
(2)解:∵DF⊥AC,BE∥DF,
∴∠BEF=∠DFE=90°,
∴∠DFC=90°,
∵DF=12,DC=BF=13,
∴CF==5,
∵BE=DF=12,
∴EF==5,
∴CE=EF+CF=10,
∴BC===2.
故BC的长为2.
10.(1)证明:在△AOE和△COD中,
,
∴△AOE≌△COD(ASA),
∴OD=OE,
又∵AO=CO,
∴四边形AECD是平行四边形;
(2)解:∵AB=BC,AO=CO,
∴OB⊥AC,
∴平行四边形AECD是菱形,
∵AC=8,
∴CO=AC=4,
在Rt△COD中,由勾股定理得:OD===3,
∴DE=2OD=6,
∴菱形AECD的面积=AC×DE=×8×6=24.
11.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠ADB=∠F,
∴BD∥EF,
∴四边形BDFE是平行四边形;
(2)解:由(1)得:四边形BDFE是平行四边形,
∴DF=BE=4,
∵四边形ABCD是平行四边形,
∴BC=AD=10,
∴CE=BC﹣BE=10﹣4=6,AD∥BC,
∴EG=,
即EG的长为.
12.解:(1)∵四边形ABCD是平行四边形,
∴AO=OC,AB∥CD.
∴∠E=∠F.
∵在△AOE与△COF中,
,
∴△AOE≌△COF(AAS);
(2)如图,连接EC、AF,
由(1)可知△AOE≌△COF,
∴OE=OF,
∵AO=CO,
∴四边形AECF是平行四边形.
13.证明:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF
∴AF=BC,
在Rt△AFE和Rt△BCA中,
,
∴△AFE≌△BCA(HL),
∴AC=EF;
(2)∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形.
14.(1)证明:∵∠A=∠ABC=90°,
∴BC∥AD,
∴∠CBE=∠DFE,
在△BEC与△FED中,
,
∴△BEC≌△FED,
∴BE=FE,
又∵E是边CD的中点,
∴CE=DE,
∴四边形BDFC是平行四边形;
(2)①BC=BD=3时,由勾股定理得,AB===2,
所以,四边形BDFC的面积=3×2=6;
②BC=CD=3时,过点C作CG⊥AF于G,则四边形AGCB是矩形,
所以,AG=BC=3,
所以,DG=AG﹣AD=3﹣1=2,
由勾股定理得,CG===,
所以,四边形BDFC的面积=3×=3;
③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾,此时不成立;
综上所述,四边形BDFC的面积是6或3.
15.(1)解:作CG⊥AD于G,如图1所示:
设PG=x,则DG=4﹣x,
在Rt△PGC中,GC2=CP2﹣PG2=17﹣x2,
在Rt△DGC中,GC2=CD2﹣GD2=52﹣(4﹣x)2=9+8x﹣x2,
∴17﹣x2=9+8x﹣x2,
解得:x=1,即PG=1,
∴GC=4,
∵DP=2AP=4,
∴AD=6,
∴S△ACD=×AD×CG=×6×4=12;
(2)证明:连接NE,如图2所示:
∵BH⊥AE,AF⊥BC,AE⊥EM,
∴∠AEB+∠NBF=∠AEB+∠EAF=∠AEB+∠MEC=90°,
∴∠NBF=∠EAF=∠MEC,
在△NBF和△EAF中,,
∴△NBF≌△EAF(AAS),
∴BF=AF,NF=EF,
∴∠ABC=45°,∠ENF=45°,
∵∠ANB=90°+∠EAF,∠CEA=90°+∠MEC,
∴∠ANB=∠CEA,
在△ANB和△CEA中,,
∴△ANB≌△CEA(SAS),
∴∠CAE=∠ABN,
∵∠NBF=∠EAF,
∴∠ABF=∠FAC=45°
∴FC=AF=BF,
∴∠ANE=∠BCD=135°,AD=BC=2AF,
在△ANE和△ECM中,,
∴△ANE≌△ECM(ASA),
∴CM=NE,
又∵NF=NE=MC,
∴AF=MC+EC,
∴AD=MC+2EC.
16.解:(1)∵E是AC的中点,
∴AE=CE,
∵AB∥CD,
∴∠AFE=∠CDE,
在△AEF和△CED中,
∵,
∴△AEF≌△CED(AAS),
∴AF=CD,
又AB∥CD,即AF∥CD,
∴四边形AFCD是平行四边形;
17.(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,
∵AM⊥BD,CN⊥BD,
∴AM∥CN,
∴CM∥AN,AM∥CN,
∴四边形AMCN是平行四边形.
(2)∵四边形AMCN是平行四边形,
∴CM=AN,
∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴DM=BN,∠MDE=∠NBF,
在△MDE和△NBF中,
,
∴△MDE≌△NBF(AAS),
∴ME=NF=3,
在Rt△DME中,∵∠DEM=90°,DE=4,ME=3,
∴DM===5,
∴BN=DM=5.
18.证明:(1)∵△ABC是等边三角形,
∴∠ABC=60°,
∵∠EFB=60°,
∴∠ABC=∠EFB,
∴EF∥DC(内错角相等,两直线平行),
∵DC=EF,
∴四边形EFCD是平行四边形;
(2)连接BE
∵BF=EF,∠EFB=60°,
∴△EFB是等边三角形,
∴EB=EF,∠EBF=60°
∵DC=EF,
∴EB=DC,
∵△ABC是等边三角形,
∴∠ACB=60°,AB=AC,
∴∠EBF=∠ACB,
∴△AEB≌△ADC,
∴AE=AD.
19.(1)证明:∵AC⊥BD,∠FCA=90°,∠CBF=∠DCB.
∴BD∥CF,CD∥BF,
∴四边形DBFC是平行四边形;
(2)解:∵四边形DBFC是平行四边形,
∴CF=BD=2,
∵AB=BC,AC⊥BD,
∴AE=CE,
作CM⊥BF于M,
∵BC平分∠DBF,
∴CE=CM,
∵∠F=45°,
∴△CFM是等腰直角三角形,
∴CM=CF=,
∴AE=CE=,
∴AC=2.
20.证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF.
在△ABE和△CDF中,,
∴△ABE≌△CDF(SAS),
∴AE=CF.
(2)证法1:∵△ABE≌△CDF,
∴∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,
∴四边形AECF是平行四边形.
证法2:如图,连接AC,与BD相交于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
又∵BE=DF,∴OB﹣BE=OD﹣DF,
∴OE=OF.
∴四边形AECF是平行四边形(对角线互相平分的四边形是平行四边形)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
