2021-2022学年湘教版七年级数学下册第2章整式的乘法单元达标测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版七年级数学下册第2章整式的乘法单元达标测试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 133.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 20:10:29 | ||
图片预览



文档简介
2021-2022学年湘教版七年级数学下册《第2章整式的乘法》单元达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.化简(﹣a2) a5所得的结果是( )
A.a7 B.﹣a7 C.a10 D.﹣a10
2.若(x﹣1)0=1成立,则x的取值范围是( )
A.x=﹣1 B.x=1 C.x≠0 D.x≠1
3.若3x=15,3y=5,则3x﹣y等于( )
A.5 B.3 C.15 D.10
4.2019新型冠状病毒的直径是0.00012mm,将0.00012用科学记数法表示是( )
A.120×10﹣6 B.12×10﹣3 C.1.2×10﹣4 D.1.2×10﹣5
5.已知多项式ax+b与2x2+2x+3的乘积展开式中不含x的一次项,且常数项为﹣9,则ab的值为( )
A. B. C.﹣8 D.﹣6
6.如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”如(8=32﹣12,16=52﹣32,即8,16均为“和谐数”),在不超过2017的正整数中,所有的“和谐数”之和为( )
A.255024 B.255054 C.255064 D.250554
7.如图,两个正方形的边长分别为a,b,如果a+b=ab=9,则阴影部分的面积为( )
A.9 B.18 C.27 D.36
8.通过计算几何图形的面积可表示一些代数恒等式,如图可表示的代数恒等式是( )
A.(a﹣b)2=a2﹣2ab+b2 B.(a+b)2=a2+2ab+b2
C.2a(a+b)=2a2+2ab D.(a+b)(a﹣b)=a2﹣b2
二.填空题(共6小题,满分30分)
9.am=2,an=3,a2m+3n= .
10.若x2+mx+16是完全平方式,则m的值是 .
11.(x2y﹣xy2)÷xy= .
12.已知4x=10,25y=10,则(x﹣2)(y﹣2)+3(xy﹣3)的值为 .
13.已知长方形面积为6y4﹣3x2y3+x2y2,它的一边长为3y2,则这个长方形另外一边长为 .
14.如图,边长为2m+3的正方形纸片剪出一个边长为m+3的正方形之后,剩余部分可剪拼成一个长方形,若拼成的长方形一边长为m,则这个长方形的周长为 .
三.解答题(共7小题,满分50分)
15.计算:
(1)(﹣t4)3+(﹣t2)6;
(2)(m4)2+(m3)2﹣m(m2)2 m3.
16.(x﹣y) (y﹣x)2 (y﹣x)3﹣(y﹣x)6.
17.先化简,再求值:[4(x﹣y)2﹣2(x﹣2y)(y+2x)]÷(﹣2y),其中x=2,y=﹣1.
18.一个正方体集装箱的棱长为0.4m.
(1)这个集装箱的体积是多少(用科学记数法表示)?
(2)若有一个小立方块的棱长为1×10﹣3m,则需要多少个这样的小立方块才能将集装箱装满?
19.欢欢与乐乐两人共同计算(2x+a)(3x+b),欢欢抄错为(2x﹣a)(3x+b),得到的结果为6x2﹣13x+6;乐乐抄错为(2x+a)(x+b),得到的结果为2x2﹣x﹣6.
(1)式子中的a、b的值各是多少?
(2)请计算出原题的正确答案.
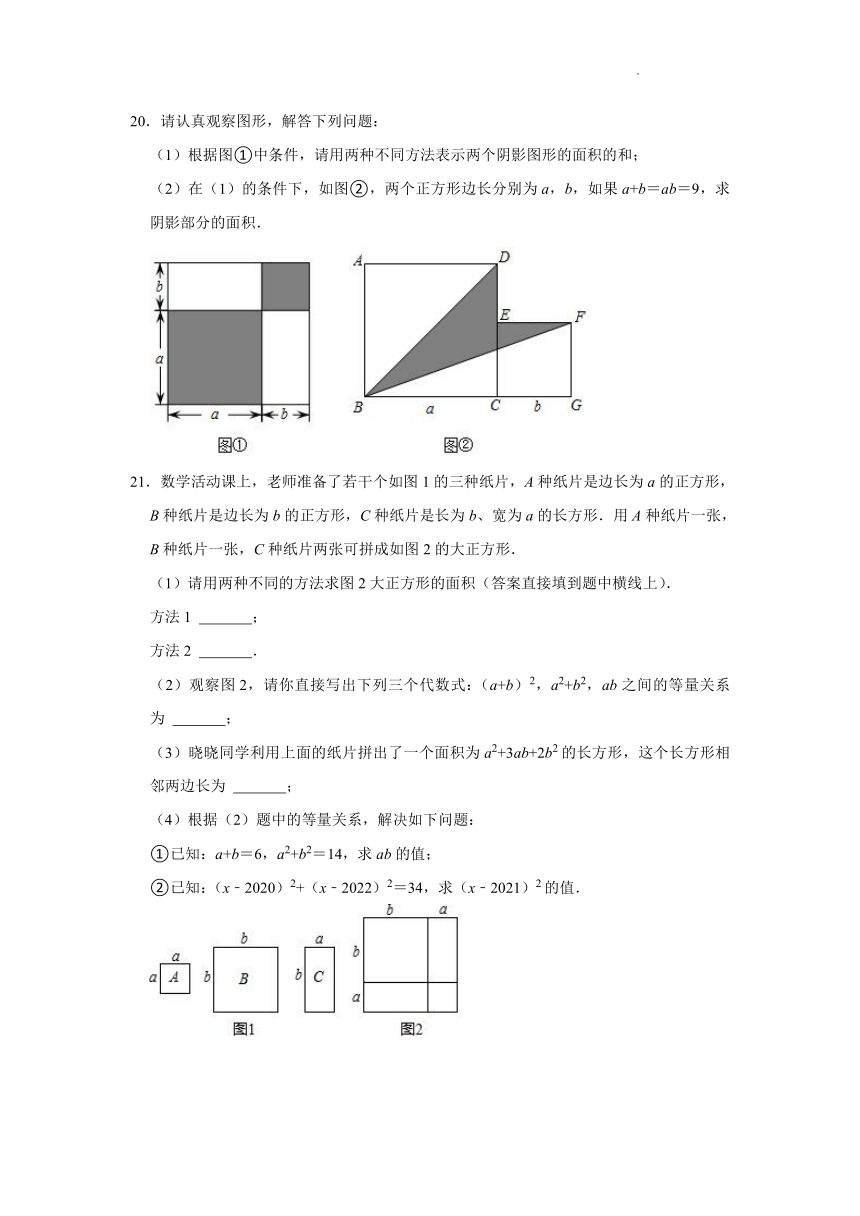
20.请认真观察图形,解答下列问题:
(1)根据图①中条件,请用两种不同方法表示两个阴影图形的面积的和;
(2)在(1)的条件下,如图②,两个正方形边长分别为a,b,如果a+b=ab=9,求阴影部分的面积.
21.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b、宽为a的长方形.用A种纸片一张,B种纸片一张,C种纸片两张可拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积(答案直接填到题中横线上).
方法1 ;
方法2 .
(2)观察图2,请你直接写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系为 ;
(3)晓晓同学利用上面的纸片拼出了一个面积为a2+3ab+2b2的长方形,这个长方形相邻两边长为 ;
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=6,a2+b2=14,求ab的值;
②已知:(x﹣2020)2+(x﹣2022)2=34,求(x﹣2021)2的值.
参考答案
一.选择题(共8小题,满分40分)
1.解:(﹣a2) a5=﹣a7,
故选:B.
2.解:由题意可知:x﹣1≠0,
x≠1
故选:D.
3.解:3x﹣y=3x÷3y=15÷5=3,
故选:B.
4.解:0.00012=1.2×10﹣4.
故选:C.
5.解:(ax+b)(2x2+2x+3)
=2ax3+2ax2+3ax+2bx2+2bx+3b
=2ax3+(2a+b)x2+(3a+2b)x+3b,
∵乘积展开式中不含x的一次项,且常数项为﹣9,
∴3a+2b=0且3b=﹣9,
则a=2,b=﹣3,
∴ab=2﹣3=,
故选:A.
6.解:设相邻的两奇数分别为2n+1,2n﹣1(n≥1,且n为正整数),
(2n+1)2﹣(2n﹣1)2=8n,
根据题意得:8n≤2017,
∴n≤252,
∴n最大为252,此时2n+1=505,2n﹣1=503,
∴32﹣12+52﹣32+...+5032﹣5012+5052﹣5032
=5052﹣12
=255024.
故选:A.
7.解:∵a+b=ab=9,
∴S=a2+b2﹣a2﹣b(a+b)=(a2+b2﹣ab)=[(a+b)2﹣3ab]=×(81﹣27)=27.
故选:C.
8.解:长方形的面积等于:2a(a+b),
也等于四个小图形的面积之和:a2+a2+ab+ab=2a2+2ab,
即2a(a+b)=2a2+2ab.
故选:C.
二.填空题(共6小题,满分30分)
9.解:am=2,an=3,
a2m=4,a3n=27
a2m+3n=a2m.a3n=4×27=108,
故答案为:108.
10.解:∵x2+mx+16是一个完全平方式,
∴x2+mx+16=(x±4)2,
=x2±8x+16.
∴m=±8,
故答案为:±8.
11.解:原式=x2y÷xy﹣xy2÷xy÷xy
=9x﹣4y+6.
故答案为:9x﹣4y+6.
12.解:∵
∴由①得4xy=10y,③
由②得25xy=10x,④
∴③×④得4xy 25xy=10y 10x,即(4×25)xy=10x+y,
∴(102)xy=10x+y,
∴102xy=10x+y,
∴2xy=x+y
(x﹣2)(y﹣2)+3(xy﹣3)
=xy﹣2x﹣2y+4+3xy﹣9
=4xy﹣2(x+y)﹣5
=4xy﹣2×2xy﹣5
=﹣5
故答案为:﹣5.
13.解:长方形另一边长为:
(6y4﹣3x2y3+x2y2)÷3y2
=2y2﹣x2y+x2,
故答案为:2y2﹣x2y+x2.
14.解:由图可以看出,长方形的长为2m+3+m+3=3m+6,拼成的长方形的宽为2m+3﹣(m+3)=m,
∴这个长方形的周长为:2(3m+6+m)=8m+12.
故答案为:(8m+12).
三.解答题(共7小题,满分50分)
15.解:(1)原式=﹣t12+t12=0;
(2)原式=m8+m6﹣m8=m6.
16.解:(x﹣y) (y﹣x)2 (y﹣x)3﹣(y﹣x)6
=﹣(x﹣y) (x﹣y)2 (x﹣y)3﹣(x﹣y)6
=﹣(x﹣y)6﹣(x﹣y)6
=﹣2(x﹣y)6.
17.解:[4(x﹣y)2﹣2(x﹣2y)(y+2x)]÷(﹣2y)
=(4x2﹣8xy+4y2+6xy﹣4x2+4y2)÷(﹣2y)
=(﹣2xy+8y2)÷(﹣2y)
=x﹣4y,
当x=2,y=﹣1时,原式=2﹣4×(﹣1)=2+4=6.
18.解:(1)∵一个正方体集装箱的棱长为0.4m,
∴这个集装箱的体积是:0.4×0.4×0.4=6.4×10﹣2(m3),
答:这个集装箱的体积是6.4×10﹣2m3;
(2)∵一个小立方块的棱长为1×10﹣3m,
∴6.4×10﹣2÷(1×10﹣3)3=64000000(个),
答:需要64000000个这样的小立方块才能将集装箱装满.
19.解:(1)根据题意可知,由于欢欢抄错了第一个多项式中的a的符号,得到的结果为6x2﹣13x+6,
那么(2x﹣a)(3x+b)=6x2+(2b﹣3a)x﹣ab=6x2﹣13x+6,
可得2b﹣3a=﹣13 ①
乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为2x2﹣x﹣6,
可知(2x+a)(x+b)=2x2﹣x﹣6
即2x2+(2b+a)x+ab=2x2﹣x﹣6,
可得2b+a=﹣1 ②,
解关于①②的方程组,可得a=3,b=﹣2;
(2)正确的式子:
(2x+3)(3x﹣2)=6x2+5x﹣6
20.解:(1)方法一:两个正方形的面积和,即a2+b2,
方法二:边长为a+b的正方形的面积减去两个空白的长方形的面积,即(a+b)2﹣2ab,
因此有a2+b2=(a+b)2﹣2ab,
(2)图②阴影部分的面积是两个边长分别为a、b的正方形的面积和减去两个直角三角形的面积,
即a2+b2﹣a×a﹣(a+b)×b
=a2+b2﹣ab
=(a2+b2﹣ab)
=[(a+b)2﹣3ab],
当a+b=ab=9时,
原式=×(81﹣27)=27,
答:阴影部分的面积为27.
21.解:(1)由题意,图2面积可分别表示为:(a+b)2和a2+b2+2àb,
故答案为:(a+b)2,a2+b2+2àb;
(2)根据(1)中两个结果可得,(a+b)2=a2+b2+2àb,
故答案为:(a+b)2=a2+b2+2àb;
(3)∵a2+3ab+2b2可分解为(a+b)(a+2b),
∴可拼成边长各为a+b,a+2b的长方形,
故答案为:a+b,a+2b;
(4)①由(2)题结果(a+b)2=a2+b2+2àb可得,
ab=====11,
②设x﹣2020=a,x﹣2022=b,则a2+b2=34,a﹣b=(x﹣2020)﹣(x﹣2022)=x﹣2020﹣x+2022=2,a+b=(x﹣2020)+(x﹣2022)=x﹣2020+x﹣2022)=2x﹣4042=2(x﹣2021),
又∵(a﹣b)2=a2﹣2ab+b2,
∴ab====15,
∴[2(x﹣2021)]2=4(x﹣2021)2=(a+b)2=a2+b2+2àb=34+2×15=34+30=64,
∴(x﹣2021)2==16.
一.选择题(共8小题,满分40分)
1.化简(﹣a2) a5所得的结果是( )
A.a7 B.﹣a7 C.a10 D.﹣a10
2.若(x﹣1)0=1成立,则x的取值范围是( )
A.x=﹣1 B.x=1 C.x≠0 D.x≠1
3.若3x=15,3y=5,则3x﹣y等于( )
A.5 B.3 C.15 D.10
4.2019新型冠状病毒的直径是0.00012mm,将0.00012用科学记数法表示是( )
A.120×10﹣6 B.12×10﹣3 C.1.2×10﹣4 D.1.2×10﹣5
5.已知多项式ax+b与2x2+2x+3的乘积展开式中不含x的一次项,且常数项为﹣9,则ab的值为( )
A. B. C.﹣8 D.﹣6
6.如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”如(8=32﹣12,16=52﹣32,即8,16均为“和谐数”),在不超过2017的正整数中,所有的“和谐数”之和为( )
A.255024 B.255054 C.255064 D.250554
7.如图,两个正方形的边长分别为a,b,如果a+b=ab=9,则阴影部分的面积为( )
A.9 B.18 C.27 D.36
8.通过计算几何图形的面积可表示一些代数恒等式,如图可表示的代数恒等式是( )
A.(a﹣b)2=a2﹣2ab+b2 B.(a+b)2=a2+2ab+b2
C.2a(a+b)=2a2+2ab D.(a+b)(a﹣b)=a2﹣b2
二.填空题(共6小题,满分30分)
9.am=2,an=3,a2m+3n= .
10.若x2+mx+16是完全平方式,则m的值是 .
11.(x2y﹣xy2)÷xy= .
12.已知4x=10,25y=10,则(x﹣2)(y﹣2)+3(xy﹣3)的值为 .
13.已知长方形面积为6y4﹣3x2y3+x2y2,它的一边长为3y2,则这个长方形另外一边长为 .
14.如图,边长为2m+3的正方形纸片剪出一个边长为m+3的正方形之后,剩余部分可剪拼成一个长方形,若拼成的长方形一边长为m,则这个长方形的周长为 .
三.解答题(共7小题,满分50分)
15.计算:
(1)(﹣t4)3+(﹣t2)6;
(2)(m4)2+(m3)2﹣m(m2)2 m3.
16.(x﹣y) (y﹣x)2 (y﹣x)3﹣(y﹣x)6.
17.先化简,再求值:[4(x﹣y)2﹣2(x﹣2y)(y+2x)]÷(﹣2y),其中x=2,y=﹣1.
18.一个正方体集装箱的棱长为0.4m.
(1)这个集装箱的体积是多少(用科学记数法表示)?
(2)若有一个小立方块的棱长为1×10﹣3m,则需要多少个这样的小立方块才能将集装箱装满?
19.欢欢与乐乐两人共同计算(2x+a)(3x+b),欢欢抄错为(2x﹣a)(3x+b),得到的结果为6x2﹣13x+6;乐乐抄错为(2x+a)(x+b),得到的结果为2x2﹣x﹣6.
(1)式子中的a、b的值各是多少?
(2)请计算出原题的正确答案.
20.请认真观察图形,解答下列问题:
(1)根据图①中条件,请用两种不同方法表示两个阴影图形的面积的和;
(2)在(1)的条件下,如图②,两个正方形边长分别为a,b,如果a+b=ab=9,求阴影部分的面积.
21.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b、宽为a的长方形.用A种纸片一张,B种纸片一张,C种纸片两张可拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积(答案直接填到题中横线上).
方法1 ;
方法2 .
(2)观察图2,请你直接写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系为 ;
(3)晓晓同学利用上面的纸片拼出了一个面积为a2+3ab+2b2的长方形,这个长方形相邻两边长为 ;
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=6,a2+b2=14,求ab的值;
②已知:(x﹣2020)2+(x﹣2022)2=34,求(x﹣2021)2的值.
参考答案
一.选择题(共8小题,满分40分)
1.解:(﹣a2) a5=﹣a7,
故选:B.
2.解:由题意可知:x﹣1≠0,
x≠1
故选:D.
3.解:3x﹣y=3x÷3y=15÷5=3,
故选:B.
4.解:0.00012=1.2×10﹣4.
故选:C.
5.解:(ax+b)(2x2+2x+3)
=2ax3+2ax2+3ax+2bx2+2bx+3b
=2ax3+(2a+b)x2+(3a+2b)x+3b,
∵乘积展开式中不含x的一次项,且常数项为﹣9,
∴3a+2b=0且3b=﹣9,
则a=2,b=﹣3,
∴ab=2﹣3=,
故选:A.
6.解:设相邻的两奇数分别为2n+1,2n﹣1(n≥1,且n为正整数),
(2n+1)2﹣(2n﹣1)2=8n,
根据题意得:8n≤2017,
∴n≤252,
∴n最大为252,此时2n+1=505,2n﹣1=503,
∴32﹣12+52﹣32+...+5032﹣5012+5052﹣5032
=5052﹣12
=255024.
故选:A.
7.解:∵a+b=ab=9,
∴S=a2+b2﹣a2﹣b(a+b)=(a2+b2﹣ab)=[(a+b)2﹣3ab]=×(81﹣27)=27.
故选:C.
8.解:长方形的面积等于:2a(a+b),
也等于四个小图形的面积之和:a2+a2+ab+ab=2a2+2ab,
即2a(a+b)=2a2+2ab.
故选:C.
二.填空题(共6小题,满分30分)
9.解:am=2,an=3,
a2m=4,a3n=27
a2m+3n=a2m.a3n=4×27=108,
故答案为:108.
10.解:∵x2+mx+16是一个完全平方式,
∴x2+mx+16=(x±4)2,
=x2±8x+16.
∴m=±8,
故答案为:±8.
11.解:原式=x2y÷xy﹣xy2÷xy÷xy
=9x﹣4y+6.
故答案为:9x﹣4y+6.
12.解:∵
∴由①得4xy=10y,③
由②得25xy=10x,④
∴③×④得4xy 25xy=10y 10x,即(4×25)xy=10x+y,
∴(102)xy=10x+y,
∴102xy=10x+y,
∴2xy=x+y
(x﹣2)(y﹣2)+3(xy﹣3)
=xy﹣2x﹣2y+4+3xy﹣9
=4xy﹣2(x+y)﹣5
=4xy﹣2×2xy﹣5
=﹣5
故答案为:﹣5.
13.解:长方形另一边长为:
(6y4﹣3x2y3+x2y2)÷3y2
=2y2﹣x2y+x2,
故答案为:2y2﹣x2y+x2.
14.解:由图可以看出,长方形的长为2m+3+m+3=3m+6,拼成的长方形的宽为2m+3﹣(m+3)=m,
∴这个长方形的周长为:2(3m+6+m)=8m+12.
故答案为:(8m+12).
三.解答题(共7小题,满分50分)
15.解:(1)原式=﹣t12+t12=0;
(2)原式=m8+m6﹣m8=m6.
16.解:(x﹣y) (y﹣x)2 (y﹣x)3﹣(y﹣x)6
=﹣(x﹣y) (x﹣y)2 (x﹣y)3﹣(x﹣y)6
=﹣(x﹣y)6﹣(x﹣y)6
=﹣2(x﹣y)6.
17.解:[4(x﹣y)2﹣2(x﹣2y)(y+2x)]÷(﹣2y)
=(4x2﹣8xy+4y2+6xy﹣4x2+4y2)÷(﹣2y)
=(﹣2xy+8y2)÷(﹣2y)
=x﹣4y,
当x=2,y=﹣1时,原式=2﹣4×(﹣1)=2+4=6.
18.解:(1)∵一个正方体集装箱的棱长为0.4m,
∴这个集装箱的体积是:0.4×0.4×0.4=6.4×10﹣2(m3),
答:这个集装箱的体积是6.4×10﹣2m3;
(2)∵一个小立方块的棱长为1×10﹣3m,
∴6.4×10﹣2÷(1×10﹣3)3=64000000(个),
答:需要64000000个这样的小立方块才能将集装箱装满.
19.解:(1)根据题意可知,由于欢欢抄错了第一个多项式中的a的符号,得到的结果为6x2﹣13x+6,
那么(2x﹣a)(3x+b)=6x2+(2b﹣3a)x﹣ab=6x2﹣13x+6,
可得2b﹣3a=﹣13 ①
乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为2x2﹣x﹣6,
可知(2x+a)(x+b)=2x2﹣x﹣6
即2x2+(2b+a)x+ab=2x2﹣x﹣6,
可得2b+a=﹣1 ②,
解关于①②的方程组,可得a=3,b=﹣2;
(2)正确的式子:
(2x+3)(3x﹣2)=6x2+5x﹣6
20.解:(1)方法一:两个正方形的面积和,即a2+b2,
方法二:边长为a+b的正方形的面积减去两个空白的长方形的面积,即(a+b)2﹣2ab,
因此有a2+b2=(a+b)2﹣2ab,
(2)图②阴影部分的面积是两个边长分别为a、b的正方形的面积和减去两个直角三角形的面积,
即a2+b2﹣a×a﹣(a+b)×b
=a2+b2﹣ab
=(a2+b2﹣ab)
=[(a+b)2﹣3ab],
当a+b=ab=9时,
原式=×(81﹣27)=27,
答:阴影部分的面积为27.
21.解:(1)由题意,图2面积可分别表示为:(a+b)2和a2+b2+2àb,
故答案为:(a+b)2,a2+b2+2àb;
(2)根据(1)中两个结果可得,(a+b)2=a2+b2+2àb,
故答案为:(a+b)2=a2+b2+2àb;
(3)∵a2+3ab+2b2可分解为(a+b)(a+2b),
∴可拼成边长各为a+b,a+2b的长方形,
故答案为:a+b,a+2b;
(4)①由(2)题结果(a+b)2=a2+b2+2àb可得,
ab=====11,
②设x﹣2020=a,x﹣2022=b,则a2+b2=34,a﹣b=(x﹣2020)﹣(x﹣2022)=x﹣2020﹣x+2022=2,a+b=(x﹣2020)+(x﹣2022)=x﹣2020+x﹣2022)=2x﹣4042=2(x﹣2021),
又∵(a﹣b)2=a2﹣2ab+b2,
∴ab====15,
∴[2(x﹣2021)]2=4(x﹣2021)2=(a+b)2=a2+b2+2àb=34+2×15=34+30=64,
∴(x﹣2021)2==16.
