2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.3.2第二课时函数的最大(小)值课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.3.2第二课时函数的最大(小)值课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 17:35:02 | ||
图片预览






文档简介
(共15张PPT)
5.3.2.2 函数的最大(小)值
2.函数的最大(小)值
在社会生活实践中,为了发挥最大的经济效益,常常遇到如何能使用料最省、产量最高,效益最大等问题,这些问题的解决常常可转化为求一个函数的最大值和最小值问题
函数在什么条件下一定有最大、最小值?他们与函数极值关系如何?
极值是一个局部概念,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小。
问题导学:
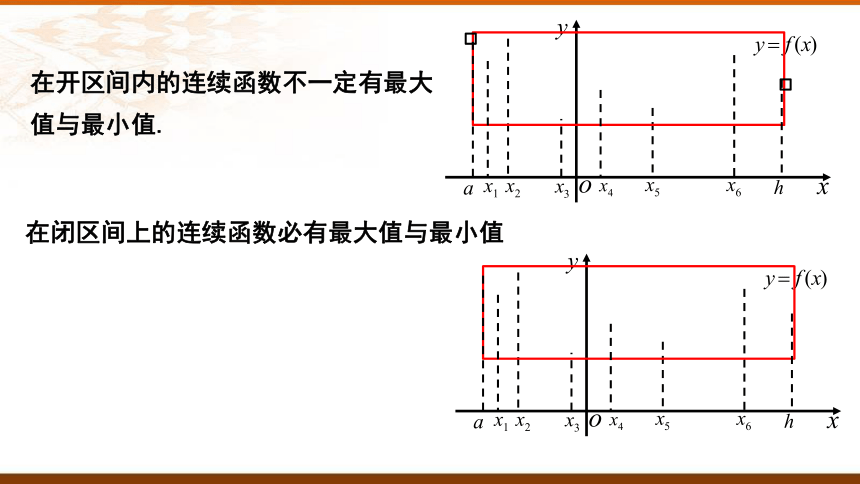
在开区间内的连续函数不一定有最大值与最小值.
在闭区间上的连续函数必有最大值与最小值
求函数的最值时,应注意以下几点:
(1)函数的极值是在局部范围内讨论问题,是一个局部概念,而函数的最值是对整个定义域而言,是在整体范围内讨论问题,是一个整体性的概念.
(2)闭区间[a,b]上的连续函数一定有最值,开区间(a,b)内的可导函数不一定有最值,但若有唯一的极值,则此极值必是函数的最值.
(3)函数在其定义域上的最大值与最小值至多各有一个,而函数的极值则可能不止一个,也可能没有极值(如常函数),并且极大值(极小值)不一定就是最大值(最小值).
函数在闭区间[a,b]上的最值:
1.如果函数在区间[a,b]上的图象是一条连续不断的曲线,那么函数必有最大值和最小值
2.最大值一定比最小值大.
3.函数的最值通常在极值点或区间端点处取得
4.只要把函数的所有极值连同端点的函数值进行比较,就可以求出函数的最大值与最小值。
一般地,利用导数求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下:
(2)将y=f(x)的各极值与端点处函数值f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
(1)求f(x)在区间(a,b)内的极值(极大值或极小值)
反思:本题属于逆向探究题型:
其基本方法最终落脚到比较极值与端点函数值大小上,从而解决问题,往往伴随有分类讨论。
1.求下列函数在给定区间上的最大值与最小值:
解:(1)因为
x
f '(x) 0
f (x)
–
+
单调递减
单调递增
又因为f(0)=-2,f(2)=20
所以,当x=2时,函数f(x)在[0,3]上取得最大值20,
当x= 时,函数f(x)在[0,3]上取得最小值 .
令 解得 .
请看课本P94:练习1
1.求下列函数在给定区间上的最大值与最小值:
x 2 ( 2, 3)
f '(x) 0
f (x)
–
+
单调递减
单调递增
解: (2)因为
又因为
所以,当x=2时,函数f(x)在 上取得最大值20,
当x= 时,函数f(x)在 上取得最小值 .
令 解得 .
请看课本P94:练习1
所以当x=1时,f(x)取得最小值.
x (0, 1) 1 ( 1, +∞)
f '(x) 0
f (x)
–
+
单调递减
单调递增
所以f(x)≥f(1)=0,即x-lnx-1≥0
解:将不等式 x-1≥lnx转化为x-lnx-1≥0
令 ,解得
故当x>0时,lnx≤x-1.
x
y
O
y=x-1
y=lnx
除点(1,0)外,曲线C1:y=x-1
在y轴右侧的部分位于曲线C2 :y=lnx的上方.
设f(x)= x-lnx-1,那么f′(x)= 1-
请看课本P94:练习2
x (-∞, -2) -2 (-2, +∞)
f '(x) 0
f (x)
–
+
单调递减
单调递增
因为f '(x)=(x+1)'ex+(x+1)(ex)'=ex+(x+1)ex =(x+2)ex
f (x)=(x+1)ex
x
y
O
1
1
-1
-2
-1
(1)求出函数f(x)的定义域;
(2)求导数f '(x)及函数f '(x)的零点;
(3)用零点将f(x) 定义域为若干个区间,列表给出f '(x)在各个区间上的正负,并得出f(x)单调性与极值;
(4)确定f(x)图象经过的一些特殊点,以及图象的变化趋势;
(5)画出f(x)的大致图象.
方法归纳:
通常可以按如下步骤画出函数f(x)的大致图象:
2.求f(x)在[a,b]上的最大值与最小值的步骤:
(1)f(x)在(a,b)内导函数为零的点,并计算出其函数值;
(2)将f(x)的各导数值为零的点的函数值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
课堂小结:
1.求最大(小)值的方法
只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值和最小值.
3.解决优化问题的基本思路:
优化问题→用函数表示的数学问题→用导数解决数学问题→优化问题的答案→优化问题
4、函数y=x3-3x2,在[-2,4]上的最大值为( )
(A) -4 (B) 0 (C) 16 (D) 20
C
学以致用:
5.3.2.2 函数的最大(小)值
2.函数的最大(小)值
在社会生活实践中,为了发挥最大的经济效益,常常遇到如何能使用料最省、产量最高,效益最大等问题,这些问题的解决常常可转化为求一个函数的最大值和最小值问题
函数在什么条件下一定有最大、最小值?他们与函数极值关系如何?
极值是一个局部概念,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小。
问题导学:
在开区间内的连续函数不一定有最大值与最小值.
在闭区间上的连续函数必有最大值与最小值
求函数的最值时,应注意以下几点:
(1)函数的极值是在局部范围内讨论问题,是一个局部概念,而函数的最值是对整个定义域而言,是在整体范围内讨论问题,是一个整体性的概念.
(2)闭区间[a,b]上的连续函数一定有最值,开区间(a,b)内的可导函数不一定有最值,但若有唯一的极值,则此极值必是函数的最值.
(3)函数在其定义域上的最大值与最小值至多各有一个,而函数的极值则可能不止一个,也可能没有极值(如常函数),并且极大值(极小值)不一定就是最大值(最小值).
函数在闭区间[a,b]上的最值:
1.如果函数在区间[a,b]上的图象是一条连续不断的曲线,那么函数必有最大值和最小值
2.最大值一定比最小值大.
3.函数的最值通常在极值点或区间端点处取得
4.只要把函数的所有极值连同端点的函数值进行比较,就可以求出函数的最大值与最小值。
一般地,利用导数求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下:
(2)将y=f(x)的各极值与端点处函数值f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
(1)求f(x)在区间(a,b)内的极值(极大值或极小值)
反思:本题属于逆向探究题型:
其基本方法最终落脚到比较极值与端点函数值大小上,从而解决问题,往往伴随有分类讨论。
1.求下列函数在给定区间上的最大值与最小值:
解:(1)因为
x
f '(x) 0
f (x)
–
+
单调递减
单调递增
又因为f(0)=-2,f(2)=20
所以,当x=2时,函数f(x)在[0,3]上取得最大值20,
当x= 时,函数f(x)在[0,3]上取得最小值 .
令 解得 .
请看课本P94:练习1
1.求下列函数在给定区间上的最大值与最小值:
x 2 ( 2, 3)
f '(x) 0
f (x)
–
+
单调递减
单调递增
解: (2)因为
又因为
所以,当x=2时,函数f(x)在 上取得最大值20,
当x= 时,函数f(x)在 上取得最小值 .
令 解得 .
请看课本P94:练习1
所以当x=1时,f(x)取得最小值.
x (0, 1) 1 ( 1, +∞)
f '(x) 0
f (x)
–
+
单调递减
单调递增
所以f(x)≥f(1)=0,即x-lnx-1≥0
解:将不等式 x-1≥lnx转化为x-lnx-1≥0
令 ,解得
故当x>0时,lnx≤x-1.
x
y
O
y=x-1
y=lnx
除点(1,0)外,曲线C1:y=x-1
在y轴右侧的部分位于曲线C2 :y=lnx的上方.
设f(x)= x-lnx-1,那么f′(x)= 1-
请看课本P94:练习2
x (-∞, -2) -2 (-2, +∞)
f '(x) 0
f (x)
–
+
单调递减
单调递增
因为f '(x)=(x+1)'ex+(x+1)(ex)'=ex+(x+1)ex =(x+2)ex
f (x)=(x+1)ex
x
y
O
1
1
-1
-2
-1
(1)求出函数f(x)的定义域;
(2)求导数f '(x)及函数f '(x)的零点;
(3)用零点将f(x) 定义域为若干个区间,列表给出f '(x)在各个区间上的正负,并得出f(x)单调性与极值;
(4)确定f(x)图象经过的一些特殊点,以及图象的变化趋势;
(5)画出f(x)的大致图象.
方法归纳:
通常可以按如下步骤画出函数f(x)的大致图象:
2.求f(x)在[a,b]上的最大值与最小值的步骤:
(1)f(x)在(a,b)内导函数为零的点,并计算出其函数值;
(2)将f(x)的各导数值为零的点的函数值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
课堂小结:
1.求最大(小)值的方法
只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值和最小值.
3.解决优化问题的基本思路:
优化问题→用函数表示的数学问题→用导数解决数学问题→优化问题的答案→优化问题
4、函数y=x3-3x2,在[-2,4]上的最大值为( )
(A) -4 (B) 0 (C) 16 (D) 20
C
学以致用:
