2021-2022学年湖南省长沙市雨花区中雅学校七年级(下)入学数学试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年湖南省长沙市雨花区中雅学校七年级(下)入学数学试卷(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 615.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 08:19:54 | ||
图片预览




文档简介
2021-2022学年湖南省长沙市雨花区中雅学校七年级(下)入学数学试卷
一、选择题(本大题共10个小题,每小题3分,共30分)
1.﹣2022的相反数是( )
A.2022 B.﹣ C. D.﹣2022
2.2021年2月25日,中国宣布脱贫攻坚战取得了全面胜利.中国的发展使世界各国广泛受益,我国倡导的“一带一路”建设,连接沿线各国人民梦想,致力于实现沿线国家的共同发展和共同富裕,世界银行报告显示,共建“一带一路”将帮助760万人摆脱极端贫困,3200万人摆脱中度贫困.下面用科学记数法表示760万正确的是( )
A.7.6×107 B.0.76×107 C.7.6×106 D.0.76×106
3.单项式﹣3x2yb与4xay是同类项,那么a、b的值分别为( )
A.2、1 B.2、0 C.0、2 D.1、2
4.下列图形不是正方体展开图的是( )
A. B.
C. D.
5.下列说法正确的是( )
A.在等式2x=a﹣2b两边除以2,可得x=a﹣b
B.在等式ab=ac两边除以a,可得b=c
C.在等式a=b两边除以(c2+2),可得
D.在等式两边除以a,可得b=c
6.下列语句中:
①有公共顶点且相等的角是对顶角;
②直线外一点到这条直线的垂线段,叫做点到直线的距离;
③两点之间直线最短;
④同一平面内,经过一点有且只有一条直线与已知直线垂直.
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
7.《九章算术》是中国古代一部重要的数学典籍,被视为“算经之首”.其中有这样一个问题:今有共头金,人出四百,盈三千四百;人出三百,盈一百.问人数、金价各几何?其大意是,假设合伙买金,每人出400钱,还剩余3400钱;每人出300钱,还剩余100钱.问人数、金价各是多少?如果设有x个人.根据题意所列方程正确的是( )
A.400x+3400=300x+100 B.400x﹣3400=300x﹣100
C. D.400x+300x=3400+100
8.如果|m﹣3|=3﹣m,那么m的取值范围是( )
A.m≤3 B.m<3 C.m≥3 D.m>3
9.如图,长方形纸片ABCD,M为AD边的中点,将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处,若∠1=30°,则∠BMC=( )
A.135° B.120° C.105° D.100°
10.已知,,,…,观察并找规律,计算的结果为( )
A.14 B.42 C.2520 D.5040
二、填空题(本大题共6个小题,每小题3分,共18分)
11.下列各数:①,②0.1,③﹣|﹣2|,④(﹣3)2,⑤,是正有理数的是 (填序号).
12.一个锐角等于它的余角的2倍,那么这个锐角是 .
13.若(a﹣1)x|a|+4=﹣6是关于x的一元一次方程,则a= .
14.已知a2﹣2a﹣1=0,则3a2﹣6a﹣4的值为 .
15.如图所示,想过P点在河两岸搭建一座桥,搭建方式最短的是线段 ,理由是 .
16.某数学老师在课外活动中做了一个有趣的游戏:首先发给A、B、C三个同学相同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成以下三个步骤:
第一步,A同学拿出二张扑克牌给B同学;
第二步,C同学拿出三张扑克牌给B同学;
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学.
请你确定,最终B同学手中剩余的扑克牌的张数为 .
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题6分,第22、23题每小题6分,第24、25题每小题6分,共72分,解答写出必要的文字说明、证明过程或演算步骤)
17.计算:.
18.解方程:.
19.先化简,再求值:(6a2﹣7ab)﹣2(3a2﹣4ab+3),其中a=﹣1,b=2.
20.小军同学在解关于x的方程去分母时,方程右边的﹣1没有乘2,因而求得方程的解为3,求m的值及方程的正确解.
21.如图,线段AB上有一点C,D为线段BC的中点,E为线段AC上一点,EC=4AE,AB=25cm,AD=20cm,求:
(1)BC的长;
(2)AE的长.
22.如图,已知∠BOC=2∠AOB,OD平分∠AOC.
(1)若∠AOB=40°,求∠COD的度数;
(2)若∠BOD=20°,求∠AOB的度数.
23.2018年元旦,某商场将甲种商品降价40%,乙种商品降价20%开展优惠促销活动.已知甲、乙两种商品的原销售单价之和为1400元,某顾客参加活动购买甲、乙各一件,共付1000元.
(1)甲、乙两种商品原销售单价各是多少元?
(2)若商场在这次促销活动中甲种商品亏损25%,乙种商品盈利25%,那么商场在这次促销活动中是盈利还是亏损了?如果是盈利,求商场销售甲、乙两种商品各一件盈利了多少元?如果是亏损,求销售甲、乙两种商品各一件亏损了多少元?
24.知识背景:
已知a、b为有理数,规定:f(a)=|a﹣2|,g(b)=|b+3|,例如:f(﹣3)=|﹣3﹣2|=5,g(﹣2)=|﹣2+3|=1.
知识应用:
(1)若f(a)+g(b)=0,求3a﹣5b的值;
(2)求f(a﹣1)+g(a﹣1)的最值;
知识迁移:
(3)若有理数a、b、c满足|a﹣b+c+3|=a+b+c﹣3,且关于x的方程ax﹣2c=2a﹣cx有无数解,f(2b﹣4)≠0,求|a+2b+c+5|﹣|a+b+c+7|﹣|﹣3﹣b|的值.
25.已知(a﹣16)x3+20x2+(b+2)x+5是关于x的二次二项式,A,B是数轴上两点,且A,B对应的数分别为a,b.
(1)求线段AB的中点C所对应的数;
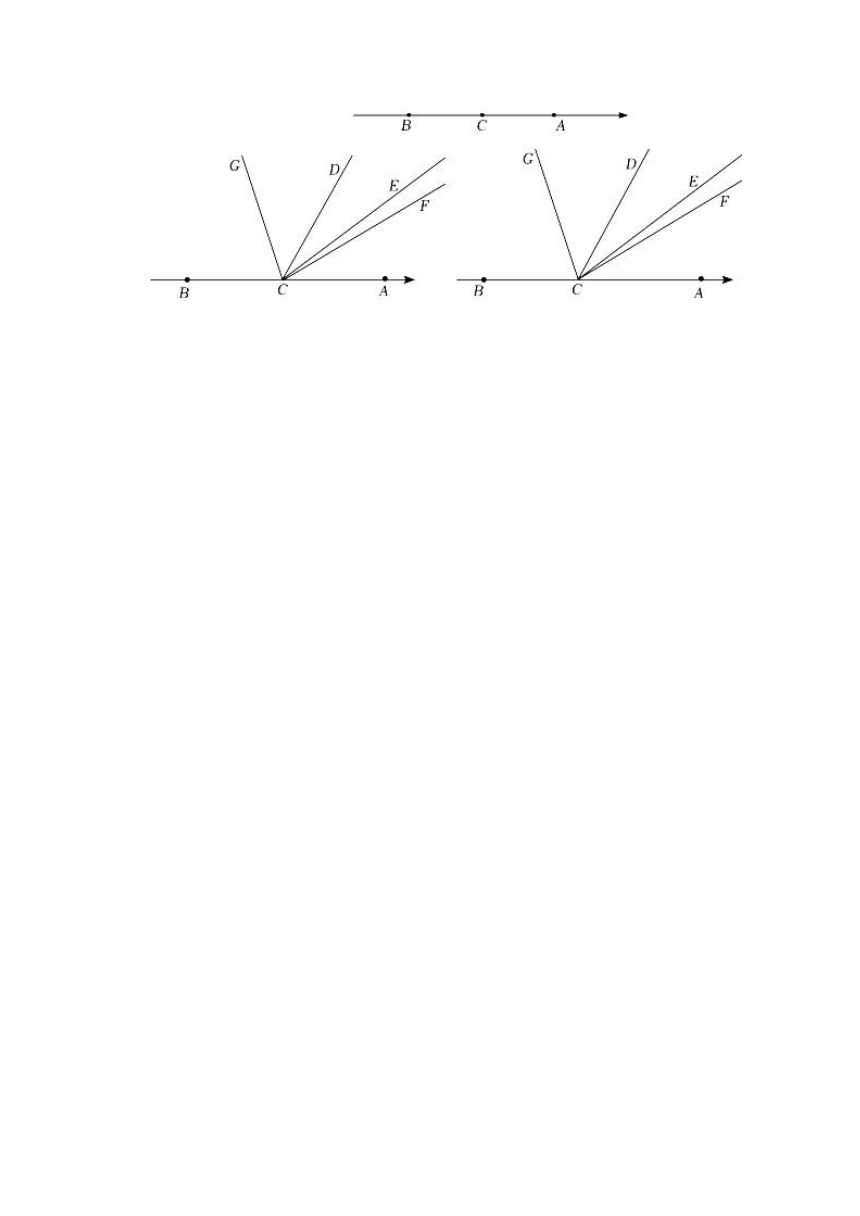
(2)如图,在数轴上方从点C出发引出射线CD,CE,CF,CG,且CF平分∠ACD,CG平分∠BCE,试猜想∠DCE与∠FCG之间是否存在确定的数量关系,并说明理由;
(3)在(2)的条件下,已知∠DCE=20°,∠ACE=30°,当∠DCE绕着点C以5°/秒的速度逆时针旋转t秒(0<t<26)时,∠ACF和∠BCG中的一个角的度数恰好是另一个角度数的两倍,求t的值.
参考答案
一、选择题(本大题共10个小题,每小题3分,共30分)
1.﹣2022的相反数是( )
A.2022 B.﹣ C. D.﹣2022
【分析】相反数的概念:只有符号不同的两个数叫做互为相反数,据此判断即可.
解:﹣2022的相反数是是2022.
故选:A.
2.2021年2月25日,中国宣布脱贫攻坚战取得了全面胜利.中国的发展使世界各国广泛受益,我国倡导的“一带一路”建设,连接沿线各国人民梦想,致力于实现沿线国家的共同发展和共同富裕,世界银行报告显示,共建“一带一路”将帮助760万人摆脱极端贫困,3200万人摆脱中度贫困.下面用科学记数法表示760万正确的是( )
A.7.6×107 B.0.76×107 C.7.6×106 D.0.76×106
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
解:760万=7600000=7.6×106.
故选:C.
3.单项式﹣3x2yb与4xay是同类项,那么a、b的值分别为( )
A.2、1 B.2、0 C.0、2 D.1、2
【分析】根据同类项的定义(所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项)求解即可.
解:∵单项式﹣3x2yb与4xay是同类项,
∴a=2,b=1.
故选:A.
4.下列图形不是正方体展开图的是( )
A. B.
C. D.
【分析】由平面图形的折叠及正方体的展开图解题.
解:A、C、D经过折叠均能围成正方体,B折叠后上边没有面,不能折成正方体.
故选:B.
5.下列说法正确的是( )
A.在等式2x=a﹣2b两边除以2,可得x=a﹣b
B.在等式ab=ac两边除以a,可得b=c
C.在等式a=b两边除以(c2+2),可得
D.在等式两边除以a,可得b=c
【分析】根据等式的性质即可求出答案.
解:A、在等式2x=a﹣2b两边除以2,可得x=﹣b,故不合题意;
B、当a=0时,该结论不成立,故不合题意;
C、由于c2+1≥1,在等式a=b两边除以(c2+1),可得,故符合题意;
D、存在等式两边乘以a,可得b=c,故不合题意;
故选:C.
6.下列语句中:
①有公共顶点且相等的角是对顶角;
②直线外一点到这条直线的垂线段,叫做点到直线的距离;
③两点之间直线最短;
④同一平面内,经过一点有且只有一条直线与已知直线垂直.
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据对顶角、线段的性质、点到直线的距离,垂线的定义逐一判断即可.
解:①有公共顶点且相等的角是对顶角,错误,
②直线外一点到这条直线的垂线段,叫做点到直线的距离,错误,
③两点之间线段最短,错误,
④在平面内,经过一点有且只有一条直线与已知直线垂直,正确,
∴上列语句中,正确的个数有1个,
故选:A.
7.《九章算术》是中国古代一部重要的数学典籍,被视为“算经之首”.其中有这样一个问题:今有共头金,人出四百,盈三千四百;人出三百,盈一百.问人数、金价各几何?其大意是,假设合伙买金,每人出400钱,还剩余3400钱;每人出300钱,还剩余100钱.问人数、金价各是多少?如果设有x个人.根据题意所列方程正确的是( )
A.400x+3400=300x+100 B.400x﹣3400=300x﹣100
C. D.400x+300x=3400+100
【分析】直接利用金的总价格不变进而得出方程即可.
解:设有x个人,根据题意可得:
400x﹣3400=300x﹣100.
故选:B.
8.如果|m﹣3|=3﹣m,那么m的取值范围是( )
A.m≤3 B.m<3 C.m≥3 D.m>3
【分析】根据绝对值的性质解答即可.
解:∵|m﹣3|=3﹣m=﹣(m﹣3),
∴m﹣3≤0,
∴m≤3.
故选:A.
9.如图,长方形纸片ABCD,M为AD边的中点,将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处,若∠1=30°,则∠BMC=( )
A.135° B.120° C.105° D.100°
【分析】根据“折叠”前后的等量关系可以得知MB和MC分别是∠AMA1和∠DMD1的角平分线,再利用平角是180°,计算求出∠BMC.
解:∵∠1=30°
∴∠AMA1+∠DMD1=180°﹣30°=150°
∵将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处,
∴MB平分∠AMA1,MC平分∠DMD1
∴∠BMA1+∠CMD1=(∠AMA1+∠DMD1)=75°
∴∠BMC=∠1+∠BMA1+∠CMD1=30°+75°=105°
故选:C.
10.已知,,,…,观察并找规律,计算的结果为( )
A.14 B.42 C.2520 D.5040
【分析】根据所给的式子,不难看出=7×6×5×4×3×2,从而可求解.
解:∵,,,…,
∴=7×6×5×4×3×2=5040,
故选:D.
二、填空题(本大题共6个小题,每小题3分,共18分)
11.下列各数:①,②0.1,③﹣|﹣2|,④(﹣3)2,⑤,是正有理数的是 ①②④ (填序号).
【分析】根据绝对值、有理数的乘方、相反数、有理数的定义解决此题.
解:①是正分数,那么①是正有理数.
②0.1是正的小数,那么②是正有理数.
③根据绝对值的定义,﹣|﹣2|=﹣2<0,那么﹣|﹣2|是负数,那么③不是正有理数.
④根据有理数的乘方,(﹣3)2=9>0,那么(﹣3)2是正有理数,那么④是正有理数.
⑤根据无理数的定义,是无理数.
综上:正有理数有①②④.
12.一个锐角等于它的余角的2倍,那么这个锐角是 60° .
【分析】可设这个锐角的度数为x,则其余角为(90°﹣x),从而可列出式子进行求解.
解:设这个锐角的度数为x,依题意得:
x=2(90°﹣x),
解得:x=60°,
故答案为:60°.
13.若(a﹣1)x|a|+4=﹣6是关于x的一元一次方程,则a= ﹣1 .
【分析】根据一元一次方程的特点求出a的值.只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程,它的一般形式是ax+b=0(a,b是常数且a≠0).
解:根据题意知:|a|=1且a﹣1≠0.
解得a=﹣1.
故答案是:﹣1.
14.已知a2﹣2a﹣1=0,则3a2﹣6a﹣4的值为 ﹣1 .
【分析】将3a2﹣6a﹣4化为3(a2﹣2a)﹣4,再整体代入计算即可.
解:∵a2﹣2a﹣1=0,即a2﹣2a=1,
∴3a2﹣6a﹣4=3(a2﹣2a)﹣4
=3×1﹣4
=﹣1,
故答案为:﹣1.
15.如图所示,想过P点在河两岸搭建一座桥,搭建方式最短的是线段 PN ,理由是 垂线段最短. .
【分析】根据垂线段最短的性质填写即可.
解:∵PN⊥MQ,
∴PN是最短的,理由是垂线段最短.
故答案为:PN,垂线段最短.
16.某数学老师在课外活动中做了一个有趣的游戏:首先发给A、B、C三个同学相同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成以下三个步骤:
第一步,A同学拿出二张扑克牌给B同学;
第二步,C同学拿出三张扑克牌给B同学;
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学.
请你确定,最终B同学手中剩余的扑克牌的张数为 7 .
【分析】本题是整式加减法的综合运用,设每人有牌x张,解答时依题意列出算式,求出答案.
解:设每人有牌x张,B同学从A同学处拿来二张扑克牌,又从C同学处拿来三张扑克牌后,
则B同学有(x+2+3)张牌,
A同学有(x﹣2)张牌,
那么给A同学后B同学手中剩余的扑克牌的张数为:x+2+3﹣(x﹣2)=x+5﹣x+2=7.
故答案为:7.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题6分,第22、23题每小题6分,第24、25题每小题6分,共72分,解答写出必要的文字说明、证明过程或演算步骤)
17.计算:.
【分析】原式先算乘方及绝对值,再算除法,最后算加减即可得到结果.
解:原式=﹣1+4﹣8+3×(﹣)
=﹣1+4﹣8+(﹣5)
=﹣10.
18.解方程:.
【分析】去分母,去括号,移项,合并同类项,系数化成1即可.
解:,
去分母,得3(x﹣2)=5(2x﹣1)﹣15,
去括号,得3x﹣6=10x﹣5﹣15,
移项,得3x﹣10x=﹣5﹣15+6,
合并同类项,得﹣7x=﹣14,
系数化成,得x=2.
19.先化简,再求值:(6a2﹣7ab)﹣2(3a2﹣4ab+3),其中a=﹣1,b=2.
【分析】直接去括号合并同类项,再把已知数据代入得出答案.
解:原式=6a2﹣7ab﹣6a2+8ab﹣6
=ab﹣6,
当a=﹣1,b=2时,
原式=﹣1×2﹣6
=﹣2﹣6
=﹣8.
20.小军同学在解关于x的方程去分母时,方程右边的﹣1没有乘2,因而求得方程的解为3,求m的值及方程的正确解.
【分析】把x=3代入方程2x﹣1=x+m﹣1得出6﹣1=3+m﹣1,求出m,再代入方程,根据等式的性质求出方程的解即可.
解:∵小军同学在解关于x的方程去分母时,方程右边的﹣1没有乘2,因而求得方程的解为3,
∴把x=3代入方程2x﹣1=x+m﹣1得:6﹣1=3+m﹣1,
解得:m=3,
则方程为,
2x﹣1=x+3﹣2,
2x﹣x=3﹣2+1,
x=2,
综上所述,m的值是3,原方程的正确的解是x=2.
21.如图,线段AB上有一点C,D为线段BC的中点,E为线段AC上一点,EC=4AE,AB=25cm,AD=20cm,求:
(1)BC的长;
(2)AE的长.
【分析】(1)根据已知条件得到BD=AB﹣AD=5cm,根据线段中点的定义即可得到结论;
(2)根据线段的和差倍分即可得到结论.
解:(1)∵AB=25cm,AD=20cm,
∴BD=AB﹣AD=5cm,
∵D为线段BC的中点,
∴BC=2BD=10cm;
(2)由(1)得,
AC=AB﹣BC=25﹣10=15(cm),
∵EC=4AE,
∴AE=AC=3cm.
22.如图,已知∠BOC=2∠AOB,OD平分∠AOC.
(1)若∠AOB=40°,求∠COD的度数;
(2)若∠BOD=20°,求∠AOB的度数.
【分析】(1)根据已知角的倍数关系求出∠AOC,再根据角平分线的定义求出∠COD;
(2)设∠AOB=x.则∠BOC=2∠AOB=2x,表示出∠AOC=3x,再根据角平分线的定义,表示∠DOA=1.5x,根据题意列方程,求出解即可.
解:(1)∵∠AOB=40°,∠BOC=2∠AOB,
∴∠BOC=80°,∠AOC=∠AOB+∠BOC=120°,
∵OD平分∠AOC,
∴∠COD=∠AOC=60°;
(2)设∠AOB=x.则∠BOC=2∠AOB=2x,
∵∠AOC=∠AOB+∠BOC,
∴∠AOC=3x,
∵OD平分∠AOC,
∴∠DOA=1.5x,
∵∠BOD=∠AOD﹣∠AOB,
∴1.5x﹣x=20°,
解得:x=40°,
∴∠AOB=x=40°.
23.2018年元旦,某商场将甲种商品降价40%,乙种商品降价20%开展优惠促销活动.已知甲、乙两种商品的原销售单价之和为1400元,某顾客参加活动购买甲、乙各一件,共付1000元.
(1)甲、乙两种商品原销售单价各是多少元?
(2)若商场在这次促销活动中甲种商品亏损25%,乙种商品盈利25%,那么商场在这次促销活动中是盈利还是亏损了?如果是盈利,求商场销售甲、乙两种商品各一件盈利了多少元?如果是亏损,求销售甲、乙两种商品各一件亏损了多少元?
【分析】(1)设甲商品原销售单价为x元,则乙商品的原销售单价为(1400﹣x)元,根据优惠后购买甲、乙各一件共需1000元,即可得出关于x的一元一次方程,解之即可得出结论;
(2)设甲商品的进价为a元/件,乙商品的进价为b元/件,根据甲、乙商品的盈亏情况,即可分别得出关于a、b的一元一次方程,解之即可求出a、b的值,再代入1000﹣a﹣b中即可找出结论.
解:(1)设甲商品原销售单价为x元,则乙商品的原销售单价为(1400﹣x)元,
根据题意得:(1﹣40%)x+(1﹣20%)(1400﹣x)=1000,
解得:x=600,
∴1400﹣x=800.
答:甲商品原销售单价为600元,乙商品的原销售单价为800元.
(2)设甲商品的进价为a元/件,乙商品的进价为b元/件,
根据题意得:(1﹣25%)a=(1﹣40%)×600,(1+25%)b=(1﹣20%)×800,
解得:a=480,b=512,
∴1000﹣a﹣b=1000﹣480﹣512=8.
答:商场在这次促销活动中盈利,盈利了8元.
24.知识背景:
已知a、b为有理数,规定:f(a)=|a﹣2|,g(b)=|b+3|,例如:f(﹣3)=|﹣3﹣2|=5,g(﹣2)=|﹣2+3|=1.
知识应用:
(1)若f(a)+g(b)=0,求3a﹣5b的值;
(2)求f(a﹣1)+g(a﹣1)的最值;
知识迁移:
(3)若有理数a、b、c满足|a﹣b+c+3|=a+b+c﹣3,且关于x的方程ax﹣2c=2a﹣cx有无数解,f(2b﹣4)≠0,求|a+2b+c+5|﹣|a+b+c+7|﹣|﹣3﹣b|的值.
【分析】(1)根据题意可得a、b的值,代入式子计算即可得到答案;
(2)由题可得f(a﹣1)=|a﹣3|,g(a﹣1)=|a+2|,借助数轴分析可得答案;
(3)根据题意可得a+c=0,进而得到b>3,然后代入所求式子,根据绝对值的性质可得答案.
解:(1)∵f(a)+g(b)=0,
∴|a﹣2|+|b+3|=0,
a=2,b=﹣3,
∴3a﹣5b=6+15=21;
(2)由题可得f(a﹣1)=|a﹣3|,g(a﹣1)=|a+2|,
∴f(a﹣1)+g(a﹣1)=|a﹣3|+|a+2|,
借助数轴分析可得,
当﹣2≤a≤3时,|a﹣3|+|a+2|有最小值,为5;
(3)∵ax﹣2c=2a﹣cx有无数解,
∴(a+c)x=2(a+c),
∴a+c=0,
∵|a﹣b+c+3|=a+b+c﹣3,
∴|﹣b+3|=b﹣3,
即b≥3,
∵f(2b﹣4)≠0,
∴|2b﹣4﹣2|≠0,
即b≠3,
∴b>3,
∴|a+2b+c+5|﹣|a+b+c+7|﹣|﹣3﹣b|
=|2b+5|﹣|b+7|﹣|﹣3﹣b|
=2b+5﹣b﹣7﹣(b+3)
=b﹣2﹣b﹣3
=﹣5.
25.已知(a﹣16)x3+20x2+(b+2)x+5是关于x的二次二项式,A,B是数轴上两点,且A,B对应的数分别为a,b.
(1)求线段AB的中点C所对应的数;
(2)如图,在数轴上方从点C出发引出射线CD,CE,CF,CG,且CF平分∠ACD,CG平分∠BCE,试猜想∠DCE与∠FCG之间是否存在确定的数量关系,并说明理由;
(3)在(2)的条件下,已知∠DCE=20°,∠ACE=30°,当∠DCE绕着点C以5°/秒的速度逆时针旋转t秒(0<t<26)时,∠ACF和∠BCG中的一个角的度数恰好是另一个角度数的两倍,求t的值.
【分析】(1)由二次二项式的定义求出a、b的值,然后利用线段中点求出C点的值;
(2)①当点C在AB之间时,如图1,②当点C在点B的右侧时,如图2,分别计算AC和AM的长,相减可得结论;
(3)本题有两个动点G和H,根据速度和时间可得点G表示的数为:﹣10+t,点H表示的数为:20+t,根据中点的定义得点D和F表示的数,由EG=BG得EG的长和点E表示的数,根据数轴上两点的距离可得DE和DF的长,相加可得结论.
解:(1)∵(a﹣16)x3+20x2+(b+2)x+5是关于x的二次二项式,
∴a=16,b=﹣2,
∴AB=16﹣(﹣2)=18,
∵点C是AB的中点,
∴C:=7,
即C点表示的数为7;
(2),理由如下:
设∠ACF=x,∠DCE=y,
∵CF平分∠ACD,
∴∠DCF=∠ACF=x,
∵CG平分∠BCE,
∴∠BCE=180°﹣x﹣(x﹣y)=180°﹣2x+y,
∠FCG=(180°﹣2x+y)+(x﹣y)=,
∵∠DCE=y,
∴;
(3)∵∠DCE=20°,∠ACE=30°,
∴∠ACD=50°,
∵CF平分∠ACD,
∴∠ACF=∠DCF,∠ECF=5°,
规定CA为0°线,顺时针为负,逆时针为正,
则CD:50°+5t,CE:30°+5t,
∠ACF=,∠BCG=∠BCE=(180°﹣30°﹣5t)=75°﹣,
若∠BCG=2∠ACF,则75°﹣=2(),
解得,
若∠ACF=2∠BCG,则=2(75°﹣),
解得t=,
∵0<t<26,
所以t的值为秒或秒.
一、选择题(本大题共10个小题,每小题3分,共30分)
1.﹣2022的相反数是( )
A.2022 B.﹣ C. D.﹣2022
2.2021年2月25日,中国宣布脱贫攻坚战取得了全面胜利.中国的发展使世界各国广泛受益,我国倡导的“一带一路”建设,连接沿线各国人民梦想,致力于实现沿线国家的共同发展和共同富裕,世界银行报告显示,共建“一带一路”将帮助760万人摆脱极端贫困,3200万人摆脱中度贫困.下面用科学记数法表示760万正确的是( )
A.7.6×107 B.0.76×107 C.7.6×106 D.0.76×106
3.单项式﹣3x2yb与4xay是同类项,那么a、b的值分别为( )
A.2、1 B.2、0 C.0、2 D.1、2
4.下列图形不是正方体展开图的是( )
A. B.
C. D.
5.下列说法正确的是( )
A.在等式2x=a﹣2b两边除以2,可得x=a﹣b
B.在等式ab=ac两边除以a,可得b=c
C.在等式a=b两边除以(c2+2),可得
D.在等式两边除以a,可得b=c
6.下列语句中:
①有公共顶点且相等的角是对顶角;
②直线外一点到这条直线的垂线段,叫做点到直线的距离;
③两点之间直线最短;
④同一平面内,经过一点有且只有一条直线与已知直线垂直.
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
7.《九章算术》是中国古代一部重要的数学典籍,被视为“算经之首”.其中有这样一个问题:今有共头金,人出四百,盈三千四百;人出三百,盈一百.问人数、金价各几何?其大意是,假设合伙买金,每人出400钱,还剩余3400钱;每人出300钱,还剩余100钱.问人数、金价各是多少?如果设有x个人.根据题意所列方程正确的是( )
A.400x+3400=300x+100 B.400x﹣3400=300x﹣100
C. D.400x+300x=3400+100
8.如果|m﹣3|=3﹣m,那么m的取值范围是( )
A.m≤3 B.m<3 C.m≥3 D.m>3
9.如图,长方形纸片ABCD,M为AD边的中点,将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处,若∠1=30°,则∠BMC=( )
A.135° B.120° C.105° D.100°
10.已知,,,…,观察并找规律,计算的结果为( )
A.14 B.42 C.2520 D.5040
二、填空题(本大题共6个小题,每小题3分,共18分)
11.下列各数:①,②0.1,③﹣|﹣2|,④(﹣3)2,⑤,是正有理数的是 (填序号).
12.一个锐角等于它的余角的2倍,那么这个锐角是 .
13.若(a﹣1)x|a|+4=﹣6是关于x的一元一次方程,则a= .
14.已知a2﹣2a﹣1=0,则3a2﹣6a﹣4的值为 .
15.如图所示,想过P点在河两岸搭建一座桥,搭建方式最短的是线段 ,理由是 .
16.某数学老师在课外活动中做了一个有趣的游戏:首先发给A、B、C三个同学相同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成以下三个步骤:
第一步,A同学拿出二张扑克牌给B同学;
第二步,C同学拿出三张扑克牌给B同学;
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学.
请你确定,最终B同学手中剩余的扑克牌的张数为 .
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题6分,第22、23题每小题6分,第24、25题每小题6分,共72分,解答写出必要的文字说明、证明过程或演算步骤)
17.计算:.
18.解方程:.
19.先化简,再求值:(6a2﹣7ab)﹣2(3a2﹣4ab+3),其中a=﹣1,b=2.
20.小军同学在解关于x的方程去分母时,方程右边的﹣1没有乘2,因而求得方程的解为3,求m的值及方程的正确解.
21.如图,线段AB上有一点C,D为线段BC的中点,E为线段AC上一点,EC=4AE,AB=25cm,AD=20cm,求:
(1)BC的长;
(2)AE的长.
22.如图,已知∠BOC=2∠AOB,OD平分∠AOC.
(1)若∠AOB=40°,求∠COD的度数;
(2)若∠BOD=20°,求∠AOB的度数.
23.2018年元旦,某商场将甲种商品降价40%,乙种商品降价20%开展优惠促销活动.已知甲、乙两种商品的原销售单价之和为1400元,某顾客参加活动购买甲、乙各一件,共付1000元.
(1)甲、乙两种商品原销售单价各是多少元?
(2)若商场在这次促销活动中甲种商品亏损25%,乙种商品盈利25%,那么商场在这次促销活动中是盈利还是亏损了?如果是盈利,求商场销售甲、乙两种商品各一件盈利了多少元?如果是亏损,求销售甲、乙两种商品各一件亏损了多少元?
24.知识背景:
已知a、b为有理数,规定:f(a)=|a﹣2|,g(b)=|b+3|,例如:f(﹣3)=|﹣3﹣2|=5,g(﹣2)=|﹣2+3|=1.
知识应用:
(1)若f(a)+g(b)=0,求3a﹣5b的值;
(2)求f(a﹣1)+g(a﹣1)的最值;
知识迁移:
(3)若有理数a、b、c满足|a﹣b+c+3|=a+b+c﹣3,且关于x的方程ax﹣2c=2a﹣cx有无数解,f(2b﹣4)≠0,求|a+2b+c+5|﹣|a+b+c+7|﹣|﹣3﹣b|的值.
25.已知(a﹣16)x3+20x2+(b+2)x+5是关于x的二次二项式,A,B是数轴上两点,且A,B对应的数分别为a,b.
(1)求线段AB的中点C所对应的数;
(2)如图,在数轴上方从点C出发引出射线CD,CE,CF,CG,且CF平分∠ACD,CG平分∠BCE,试猜想∠DCE与∠FCG之间是否存在确定的数量关系,并说明理由;
(3)在(2)的条件下,已知∠DCE=20°,∠ACE=30°,当∠DCE绕着点C以5°/秒的速度逆时针旋转t秒(0<t<26)时,∠ACF和∠BCG中的一个角的度数恰好是另一个角度数的两倍,求t的值.
参考答案
一、选择题(本大题共10个小题,每小题3分,共30分)
1.﹣2022的相反数是( )
A.2022 B.﹣ C. D.﹣2022
【分析】相反数的概念:只有符号不同的两个数叫做互为相反数,据此判断即可.
解:﹣2022的相反数是是2022.
故选:A.
2.2021年2月25日,中国宣布脱贫攻坚战取得了全面胜利.中国的发展使世界各国广泛受益,我国倡导的“一带一路”建设,连接沿线各国人民梦想,致力于实现沿线国家的共同发展和共同富裕,世界银行报告显示,共建“一带一路”将帮助760万人摆脱极端贫困,3200万人摆脱中度贫困.下面用科学记数法表示760万正确的是( )
A.7.6×107 B.0.76×107 C.7.6×106 D.0.76×106
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
解:760万=7600000=7.6×106.
故选:C.
3.单项式﹣3x2yb与4xay是同类项,那么a、b的值分别为( )
A.2、1 B.2、0 C.0、2 D.1、2
【分析】根据同类项的定义(所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项)求解即可.
解:∵单项式﹣3x2yb与4xay是同类项,
∴a=2,b=1.
故选:A.
4.下列图形不是正方体展开图的是( )
A. B.
C. D.
【分析】由平面图形的折叠及正方体的展开图解题.
解:A、C、D经过折叠均能围成正方体,B折叠后上边没有面,不能折成正方体.
故选:B.
5.下列说法正确的是( )
A.在等式2x=a﹣2b两边除以2,可得x=a﹣b
B.在等式ab=ac两边除以a,可得b=c
C.在等式a=b两边除以(c2+2),可得
D.在等式两边除以a,可得b=c
【分析】根据等式的性质即可求出答案.
解:A、在等式2x=a﹣2b两边除以2,可得x=﹣b,故不合题意;
B、当a=0时,该结论不成立,故不合题意;
C、由于c2+1≥1,在等式a=b两边除以(c2+1),可得,故符合题意;
D、存在等式两边乘以a,可得b=c,故不合题意;
故选:C.
6.下列语句中:
①有公共顶点且相等的角是对顶角;
②直线外一点到这条直线的垂线段,叫做点到直线的距离;
③两点之间直线最短;
④同一平面内,经过一点有且只有一条直线与已知直线垂直.
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据对顶角、线段的性质、点到直线的距离,垂线的定义逐一判断即可.
解:①有公共顶点且相等的角是对顶角,错误,
②直线外一点到这条直线的垂线段,叫做点到直线的距离,错误,
③两点之间线段最短,错误,
④在平面内,经过一点有且只有一条直线与已知直线垂直,正确,
∴上列语句中,正确的个数有1个,
故选:A.
7.《九章算术》是中国古代一部重要的数学典籍,被视为“算经之首”.其中有这样一个问题:今有共头金,人出四百,盈三千四百;人出三百,盈一百.问人数、金价各几何?其大意是,假设合伙买金,每人出400钱,还剩余3400钱;每人出300钱,还剩余100钱.问人数、金价各是多少?如果设有x个人.根据题意所列方程正确的是( )
A.400x+3400=300x+100 B.400x﹣3400=300x﹣100
C. D.400x+300x=3400+100
【分析】直接利用金的总价格不变进而得出方程即可.
解:设有x个人,根据题意可得:
400x﹣3400=300x﹣100.
故选:B.
8.如果|m﹣3|=3﹣m,那么m的取值范围是( )
A.m≤3 B.m<3 C.m≥3 D.m>3
【分析】根据绝对值的性质解答即可.
解:∵|m﹣3|=3﹣m=﹣(m﹣3),
∴m﹣3≤0,
∴m≤3.
故选:A.
9.如图,长方形纸片ABCD,M为AD边的中点,将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处,若∠1=30°,则∠BMC=( )
A.135° B.120° C.105° D.100°
【分析】根据“折叠”前后的等量关系可以得知MB和MC分别是∠AMA1和∠DMD1的角平分线,再利用平角是180°,计算求出∠BMC.
解:∵∠1=30°
∴∠AMA1+∠DMD1=180°﹣30°=150°
∵将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处,
∴MB平分∠AMA1,MC平分∠DMD1
∴∠BMA1+∠CMD1=(∠AMA1+∠DMD1)=75°
∴∠BMC=∠1+∠BMA1+∠CMD1=30°+75°=105°
故选:C.
10.已知,,,…,观察并找规律,计算的结果为( )
A.14 B.42 C.2520 D.5040
【分析】根据所给的式子,不难看出=7×6×5×4×3×2,从而可求解.
解:∵,,,…,
∴=7×6×5×4×3×2=5040,
故选:D.
二、填空题(本大题共6个小题,每小题3分,共18分)
11.下列各数:①,②0.1,③﹣|﹣2|,④(﹣3)2,⑤,是正有理数的是 ①②④ (填序号).
【分析】根据绝对值、有理数的乘方、相反数、有理数的定义解决此题.
解:①是正分数,那么①是正有理数.
②0.1是正的小数,那么②是正有理数.
③根据绝对值的定义,﹣|﹣2|=﹣2<0,那么﹣|﹣2|是负数,那么③不是正有理数.
④根据有理数的乘方,(﹣3)2=9>0,那么(﹣3)2是正有理数,那么④是正有理数.
⑤根据无理数的定义,是无理数.
综上:正有理数有①②④.
12.一个锐角等于它的余角的2倍,那么这个锐角是 60° .
【分析】可设这个锐角的度数为x,则其余角为(90°﹣x),从而可列出式子进行求解.
解:设这个锐角的度数为x,依题意得:
x=2(90°﹣x),
解得:x=60°,
故答案为:60°.
13.若(a﹣1)x|a|+4=﹣6是关于x的一元一次方程,则a= ﹣1 .
【分析】根据一元一次方程的特点求出a的值.只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程,它的一般形式是ax+b=0(a,b是常数且a≠0).
解:根据题意知:|a|=1且a﹣1≠0.
解得a=﹣1.
故答案是:﹣1.
14.已知a2﹣2a﹣1=0,则3a2﹣6a﹣4的值为 ﹣1 .
【分析】将3a2﹣6a﹣4化为3(a2﹣2a)﹣4,再整体代入计算即可.
解:∵a2﹣2a﹣1=0,即a2﹣2a=1,
∴3a2﹣6a﹣4=3(a2﹣2a)﹣4
=3×1﹣4
=﹣1,
故答案为:﹣1.
15.如图所示,想过P点在河两岸搭建一座桥,搭建方式最短的是线段 PN ,理由是 垂线段最短. .
【分析】根据垂线段最短的性质填写即可.
解:∵PN⊥MQ,
∴PN是最短的,理由是垂线段最短.
故答案为:PN,垂线段最短.
16.某数学老师在课外活动中做了一个有趣的游戏:首先发给A、B、C三个同学相同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成以下三个步骤:
第一步,A同学拿出二张扑克牌给B同学;
第二步,C同学拿出三张扑克牌给B同学;
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学.
请你确定,最终B同学手中剩余的扑克牌的张数为 7 .
【分析】本题是整式加减法的综合运用,设每人有牌x张,解答时依题意列出算式,求出答案.
解:设每人有牌x张,B同学从A同学处拿来二张扑克牌,又从C同学处拿来三张扑克牌后,
则B同学有(x+2+3)张牌,
A同学有(x﹣2)张牌,
那么给A同学后B同学手中剩余的扑克牌的张数为:x+2+3﹣(x﹣2)=x+5﹣x+2=7.
故答案为:7.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题6分,第22、23题每小题6分,第24、25题每小题6分,共72分,解答写出必要的文字说明、证明过程或演算步骤)
17.计算:.
【分析】原式先算乘方及绝对值,再算除法,最后算加减即可得到结果.
解:原式=﹣1+4﹣8+3×(﹣)
=﹣1+4﹣8+(﹣5)
=﹣10.
18.解方程:.
【分析】去分母,去括号,移项,合并同类项,系数化成1即可.
解:,
去分母,得3(x﹣2)=5(2x﹣1)﹣15,
去括号,得3x﹣6=10x﹣5﹣15,
移项,得3x﹣10x=﹣5﹣15+6,
合并同类项,得﹣7x=﹣14,
系数化成,得x=2.
19.先化简,再求值:(6a2﹣7ab)﹣2(3a2﹣4ab+3),其中a=﹣1,b=2.
【分析】直接去括号合并同类项,再把已知数据代入得出答案.
解:原式=6a2﹣7ab﹣6a2+8ab﹣6
=ab﹣6,
当a=﹣1,b=2时,
原式=﹣1×2﹣6
=﹣2﹣6
=﹣8.
20.小军同学在解关于x的方程去分母时,方程右边的﹣1没有乘2,因而求得方程的解为3,求m的值及方程的正确解.
【分析】把x=3代入方程2x﹣1=x+m﹣1得出6﹣1=3+m﹣1,求出m,再代入方程,根据等式的性质求出方程的解即可.
解:∵小军同学在解关于x的方程去分母时,方程右边的﹣1没有乘2,因而求得方程的解为3,
∴把x=3代入方程2x﹣1=x+m﹣1得:6﹣1=3+m﹣1,
解得:m=3,
则方程为,
2x﹣1=x+3﹣2,
2x﹣x=3﹣2+1,
x=2,
综上所述,m的值是3,原方程的正确的解是x=2.
21.如图,线段AB上有一点C,D为线段BC的中点,E为线段AC上一点,EC=4AE,AB=25cm,AD=20cm,求:
(1)BC的长;
(2)AE的长.
【分析】(1)根据已知条件得到BD=AB﹣AD=5cm,根据线段中点的定义即可得到结论;
(2)根据线段的和差倍分即可得到结论.
解:(1)∵AB=25cm,AD=20cm,
∴BD=AB﹣AD=5cm,
∵D为线段BC的中点,
∴BC=2BD=10cm;
(2)由(1)得,
AC=AB﹣BC=25﹣10=15(cm),
∵EC=4AE,
∴AE=AC=3cm.
22.如图,已知∠BOC=2∠AOB,OD平分∠AOC.
(1)若∠AOB=40°,求∠COD的度数;
(2)若∠BOD=20°,求∠AOB的度数.
【分析】(1)根据已知角的倍数关系求出∠AOC,再根据角平分线的定义求出∠COD;
(2)设∠AOB=x.则∠BOC=2∠AOB=2x,表示出∠AOC=3x,再根据角平分线的定义,表示∠DOA=1.5x,根据题意列方程,求出解即可.
解:(1)∵∠AOB=40°,∠BOC=2∠AOB,
∴∠BOC=80°,∠AOC=∠AOB+∠BOC=120°,
∵OD平分∠AOC,
∴∠COD=∠AOC=60°;
(2)设∠AOB=x.则∠BOC=2∠AOB=2x,
∵∠AOC=∠AOB+∠BOC,
∴∠AOC=3x,
∵OD平分∠AOC,
∴∠DOA=1.5x,
∵∠BOD=∠AOD﹣∠AOB,
∴1.5x﹣x=20°,
解得:x=40°,
∴∠AOB=x=40°.
23.2018年元旦,某商场将甲种商品降价40%,乙种商品降价20%开展优惠促销活动.已知甲、乙两种商品的原销售单价之和为1400元,某顾客参加活动购买甲、乙各一件,共付1000元.
(1)甲、乙两种商品原销售单价各是多少元?
(2)若商场在这次促销活动中甲种商品亏损25%,乙种商品盈利25%,那么商场在这次促销活动中是盈利还是亏损了?如果是盈利,求商场销售甲、乙两种商品各一件盈利了多少元?如果是亏损,求销售甲、乙两种商品各一件亏损了多少元?
【分析】(1)设甲商品原销售单价为x元,则乙商品的原销售单价为(1400﹣x)元,根据优惠后购买甲、乙各一件共需1000元,即可得出关于x的一元一次方程,解之即可得出结论;
(2)设甲商品的进价为a元/件,乙商品的进价为b元/件,根据甲、乙商品的盈亏情况,即可分别得出关于a、b的一元一次方程,解之即可求出a、b的值,再代入1000﹣a﹣b中即可找出结论.
解:(1)设甲商品原销售单价为x元,则乙商品的原销售单价为(1400﹣x)元,
根据题意得:(1﹣40%)x+(1﹣20%)(1400﹣x)=1000,
解得:x=600,
∴1400﹣x=800.
答:甲商品原销售单价为600元,乙商品的原销售单价为800元.
(2)设甲商品的进价为a元/件,乙商品的进价为b元/件,
根据题意得:(1﹣25%)a=(1﹣40%)×600,(1+25%)b=(1﹣20%)×800,
解得:a=480,b=512,
∴1000﹣a﹣b=1000﹣480﹣512=8.
答:商场在这次促销活动中盈利,盈利了8元.
24.知识背景:
已知a、b为有理数,规定:f(a)=|a﹣2|,g(b)=|b+3|,例如:f(﹣3)=|﹣3﹣2|=5,g(﹣2)=|﹣2+3|=1.
知识应用:
(1)若f(a)+g(b)=0,求3a﹣5b的值;
(2)求f(a﹣1)+g(a﹣1)的最值;
知识迁移:
(3)若有理数a、b、c满足|a﹣b+c+3|=a+b+c﹣3,且关于x的方程ax﹣2c=2a﹣cx有无数解,f(2b﹣4)≠0,求|a+2b+c+5|﹣|a+b+c+7|﹣|﹣3﹣b|的值.
【分析】(1)根据题意可得a、b的值,代入式子计算即可得到答案;
(2)由题可得f(a﹣1)=|a﹣3|,g(a﹣1)=|a+2|,借助数轴分析可得答案;
(3)根据题意可得a+c=0,进而得到b>3,然后代入所求式子,根据绝对值的性质可得答案.
解:(1)∵f(a)+g(b)=0,
∴|a﹣2|+|b+3|=0,
a=2,b=﹣3,
∴3a﹣5b=6+15=21;
(2)由题可得f(a﹣1)=|a﹣3|,g(a﹣1)=|a+2|,
∴f(a﹣1)+g(a﹣1)=|a﹣3|+|a+2|,
借助数轴分析可得,
当﹣2≤a≤3时,|a﹣3|+|a+2|有最小值,为5;
(3)∵ax﹣2c=2a﹣cx有无数解,
∴(a+c)x=2(a+c),
∴a+c=0,
∵|a﹣b+c+3|=a+b+c﹣3,
∴|﹣b+3|=b﹣3,
即b≥3,
∵f(2b﹣4)≠0,
∴|2b﹣4﹣2|≠0,
即b≠3,
∴b>3,
∴|a+2b+c+5|﹣|a+b+c+7|﹣|﹣3﹣b|
=|2b+5|﹣|b+7|﹣|﹣3﹣b|
=2b+5﹣b﹣7﹣(b+3)
=b﹣2﹣b﹣3
=﹣5.
25.已知(a﹣16)x3+20x2+(b+2)x+5是关于x的二次二项式,A,B是数轴上两点,且A,B对应的数分别为a,b.
(1)求线段AB的中点C所对应的数;
(2)如图,在数轴上方从点C出发引出射线CD,CE,CF,CG,且CF平分∠ACD,CG平分∠BCE,试猜想∠DCE与∠FCG之间是否存在确定的数量关系,并说明理由;
(3)在(2)的条件下,已知∠DCE=20°,∠ACE=30°,当∠DCE绕着点C以5°/秒的速度逆时针旋转t秒(0<t<26)时,∠ACF和∠BCG中的一个角的度数恰好是另一个角度数的两倍,求t的值.
【分析】(1)由二次二项式的定义求出a、b的值,然后利用线段中点求出C点的值;
(2)①当点C在AB之间时,如图1,②当点C在点B的右侧时,如图2,分别计算AC和AM的长,相减可得结论;
(3)本题有两个动点G和H,根据速度和时间可得点G表示的数为:﹣10+t,点H表示的数为:20+t,根据中点的定义得点D和F表示的数,由EG=BG得EG的长和点E表示的数,根据数轴上两点的距离可得DE和DF的长,相加可得结论.
解:(1)∵(a﹣16)x3+20x2+(b+2)x+5是关于x的二次二项式,
∴a=16,b=﹣2,
∴AB=16﹣(﹣2)=18,
∵点C是AB的中点,
∴C:=7,
即C点表示的数为7;
(2),理由如下:
设∠ACF=x,∠DCE=y,
∵CF平分∠ACD,
∴∠DCF=∠ACF=x,
∵CG平分∠BCE,
∴∠BCE=180°﹣x﹣(x﹣y)=180°﹣2x+y,
∠FCG=(180°﹣2x+y)+(x﹣y)=,
∵∠DCE=y,
∴;
(3)∵∠DCE=20°,∠ACE=30°,
∴∠ACD=50°,
∵CF平分∠ACD,
∴∠ACF=∠DCF,∠ECF=5°,
规定CA为0°线,顺时针为负,逆时针为正,
则CD:50°+5t,CE:30°+5t,
∠ACF=,∠BCG=∠BCE=(180°﹣30°﹣5t)=75°﹣,
若∠BCG=2∠ACF,则75°﹣=2(),
解得,
若∠ACF=2∠BCG,则=2(75°﹣),
解得t=,
∵0<t<26,
所以t的值为秒或秒.
同课章节目录
