华东师大版八年级下册数学第17章 函数及其图象 课件(共21张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学第17章 函数及其图象 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 517.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
复习题
一次函数复习
华师大版八年级数学(下册)
自主求知目标
1.知道一次函数与正比例函数的意义,及它们之间的关系。
2.能写出具体问题中正比例关系与一次函数关系的解析式。
3.会用待定系数法确定一次函数的解析式。 4.进一步巩固一次函数的相关知识,初步学会从数学的角度提出问题,并能综合运用所学知识和技能解决问题。
一.常量、变量:
在一个变化过程中,数值发生变化的量叫做 变量 ;数值始终不变的量叫做 常量 ;
返回引入
二、函数的概念:
函数的定义:一般的,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
三、正比例函数与一次函数的概念:
一般地,形如y=kx(k为常数,且k≠0)
的函数叫做正比例函数.其中k叫做比例系数。
当b =0 时,y=kx+b 即为 y=kx,
所以正比例函数,是一次函数的特例.
一般地,形如y=kx+b(k,b为常数,且k≠0)
的函数叫做一次函数.
(1)图象:正比例函数y= kx (k 是常数,k≠0)) 的图象是经过原点的一条直线,我们称它为直线y= kx 。
(2)性质:当k>0时,直线y= kx经过第三,一象限,从左向右上升,即随着x的增大y也增大;当k<0时,直线y= kx经过二,四象限,从左向右下降,即随着 x的增大y反而减小。
四.正比例函数的图象与性质:
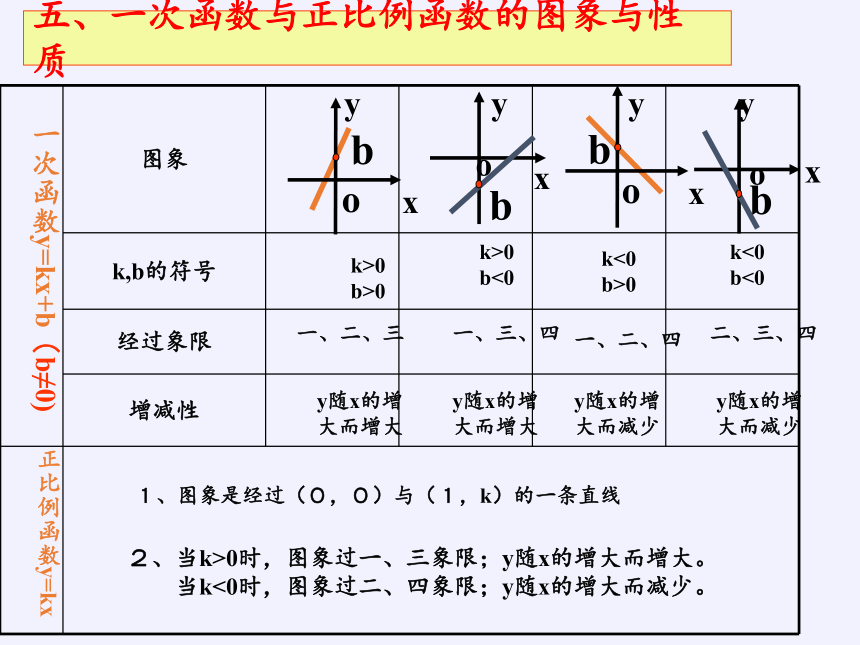
五、一次函数与正比例函数的图象与性质
一次函数y=kx+b(b≠0) 图象
k,b的符号
经过象限
增减性
正比例函数y=kx
x
y
o
b
x
y
o
b
x
y
o
b
x
y
o
b
y随x的增
大而增大
y随x的增
大而增大
y随x的增
大而减少
y随x的增
大而减少
一、二、三
一、三、四
一、二、四
二、三、四
1、图象是经过(0,0)与(1,k)的一条直线
2、当k>0时,图象过一、三象限;y随x的增大而增大。
当k<0时,图象过二、四象限;y随x的增大而减少。
k>0
b>0
k>0
b<0
k<0
b>0
k<0
b<0
例题讲解
例1 (1)若y=5x3m-2是正比例函数,m= 。
(2)若 是正比例函数,m= 。
1
-2
1、直线y=kx+b经过一、二、四象限,则
K 0, b 0.
<
>
此时,直线y=bx+k的图象只能是( )
D
专项训练(1):
2、已知直线y=kx+b平行与直线y=-2x,且与y轴交于点(0,-2),则k=___,b=___.
在同一坐标系中画出y=kx+b和y=-2x的图像。
直线y=kx+b可以由直线y=-2x经过怎样平移得到?
-2
-2
专项训练(2):
3.函数 当k____时y 随x的增大而增大 。
4.若一次函数y=x+b的图象过点A(1,-1),则b=__________。
-2
5.根据如图所示的条件,求直线的表达式。
专项训练(3):
6、柴油机在工作时油箱中的余油量Q(千克)与工作时间t(小时)成一次函数关系,当工作开始时油箱中有油40千克,工作3.5小时后,油箱中余油22.5千克
写出余油量Q与时间t的函数关系式.
解:设所求函数关系式为:Q=kt+b。
把t=0,Q=40;t=3.5,Q=22.5分别代入上式,得
解得
解析式为:Q=-5t+40
(0≤t≤8)
专项训练(4):
巩固练习
1若函数y=(6+3m)x+n-4是一次函数,则应满足的条件是_____;若是正比例函数,则应满足的条件是_____;若m=1,n=-2,则函数关系式是_____。
2若函数y=-2x+(m-3)m 的图像过原点,则m的值为____
3直线过(-1,3) 且与y=-2-x平行, 其解析式为______
4把直线y=3x+2沿着y轴向下平移1个单位,则得到直线_____
这节课,我的收获是---
1.梳理本章前几节知识脉络,加强知识点的巩固和理解.
2.进一步学会函数的研究方法,提高解题的灵活性.
3.对综合性题目,会合理使用数学思想方法探究解决.
大食堂:
P60习题A组 第3.4.5题.
小灶:
练习册P83第13题.
祝你成功!
独立
作业
驶向胜利的彼岸
数学源于生活,又服务于生活.如果你真心投入于数学学习,数学将无愧于你,助你到达胜利的彼岸.同学们,让我们热爱数学吧!
赠语:
再见!
知识的升华
独立
作业
P60习题A组 第3.4.5题.
祝你成功!
驶向胜利的彼岸
谢 谢
复习题
一次函数复习
华师大版八年级数学(下册)
自主求知目标
1.知道一次函数与正比例函数的意义,及它们之间的关系。
2.能写出具体问题中正比例关系与一次函数关系的解析式。
3.会用待定系数法确定一次函数的解析式。 4.进一步巩固一次函数的相关知识,初步学会从数学的角度提出问题,并能综合运用所学知识和技能解决问题。
一.常量、变量:
在一个变化过程中,数值发生变化的量叫做 变量 ;数值始终不变的量叫做 常量 ;
返回引入
二、函数的概念:
函数的定义:一般的,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
三、正比例函数与一次函数的概念:
一般地,形如y=kx(k为常数,且k≠0)
的函数叫做正比例函数.其中k叫做比例系数。
当b =0 时,y=kx+b 即为 y=kx,
所以正比例函数,是一次函数的特例.
一般地,形如y=kx+b(k,b为常数,且k≠0)
的函数叫做一次函数.
(1)图象:正比例函数y= kx (k 是常数,k≠0)) 的图象是经过原点的一条直线,我们称它为直线y= kx 。
(2)性质:当k>0时,直线y= kx经过第三,一象限,从左向右上升,即随着x的增大y也增大;当k<0时,直线y= kx经过二,四象限,从左向右下降,即随着 x的增大y反而减小。
四.正比例函数的图象与性质:
五、一次函数与正比例函数的图象与性质
一次函数y=kx+b(b≠0) 图象
k,b的符号
经过象限
增减性
正比例函数y=kx
x
y
o
b
x
y
o
b
x
y
o
b
x
y
o
b
y随x的增
大而增大
y随x的增
大而增大
y随x的增
大而减少
y随x的增
大而减少
一、二、三
一、三、四
一、二、四
二、三、四
1、图象是经过(0,0)与(1,k)的一条直线
2、当k>0时,图象过一、三象限;y随x的增大而增大。
当k<0时,图象过二、四象限;y随x的增大而减少。
k>0
b>0
k>0
b<0
k<0
b>0
k<0
b<0
例题讲解
例1 (1)若y=5x3m-2是正比例函数,m= 。
(2)若 是正比例函数,m= 。
1
-2
1、直线y=kx+b经过一、二、四象限,则
K 0, b 0.
<
>
此时,直线y=bx+k的图象只能是( )
D
专项训练(1):
2、已知直线y=kx+b平行与直线y=-2x,且与y轴交于点(0,-2),则k=___,b=___.
在同一坐标系中画出y=kx+b和y=-2x的图像。
直线y=kx+b可以由直线y=-2x经过怎样平移得到?
-2
-2
专项训练(2):
3.函数 当k____时y 随x的增大而增大 。
4.若一次函数y=x+b的图象过点A(1,-1),则b=__________。
-2
5.根据如图所示的条件,求直线的表达式。
专项训练(3):
6、柴油机在工作时油箱中的余油量Q(千克)与工作时间t(小时)成一次函数关系,当工作开始时油箱中有油40千克,工作3.5小时后,油箱中余油22.5千克
写出余油量Q与时间t的函数关系式.
解:设所求函数关系式为:Q=kt+b。
把t=0,Q=40;t=3.5,Q=22.5分别代入上式,得
解得
解析式为:Q=-5t+40
(0≤t≤8)
专项训练(4):
巩固练习
1若函数y=(6+3m)x+n-4是一次函数,则应满足的条件是_____;若是正比例函数,则应满足的条件是_____;若m=1,n=-2,则函数关系式是_____。
2若函数y=-2x+(m-3)m 的图像过原点,则m的值为____
3直线过(-1,3) 且与y=-2-x平行, 其解析式为______
4把直线y=3x+2沿着y轴向下平移1个单位,则得到直线_____
这节课,我的收获是---
1.梳理本章前几节知识脉络,加强知识点的巩固和理解.
2.进一步学会函数的研究方法,提高解题的灵活性.
3.对综合性题目,会合理使用数学思想方法探究解决.
大食堂:
P60习题A组 第3.4.5题.
小灶:
练习册P83第13题.
祝你成功!
独立
作业
驶向胜利的彼岸
数学源于生活,又服务于生活.如果你真心投入于数学学习,数学将无愧于你,助你到达胜利的彼岸.同学们,让我们热爱数学吧!
赠语:
再见!
知识的升华
独立
作业
P60习题A组 第3.4.5题.
祝你成功!
驶向胜利的彼岸
谢 谢
