2021-2022学年冀教版七年级数学下册第7章相交线与平行线单元综合测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版七年级数学下册第7章相交线与平行线单元综合测试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 235.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 20:17:02 | ||
图片预览


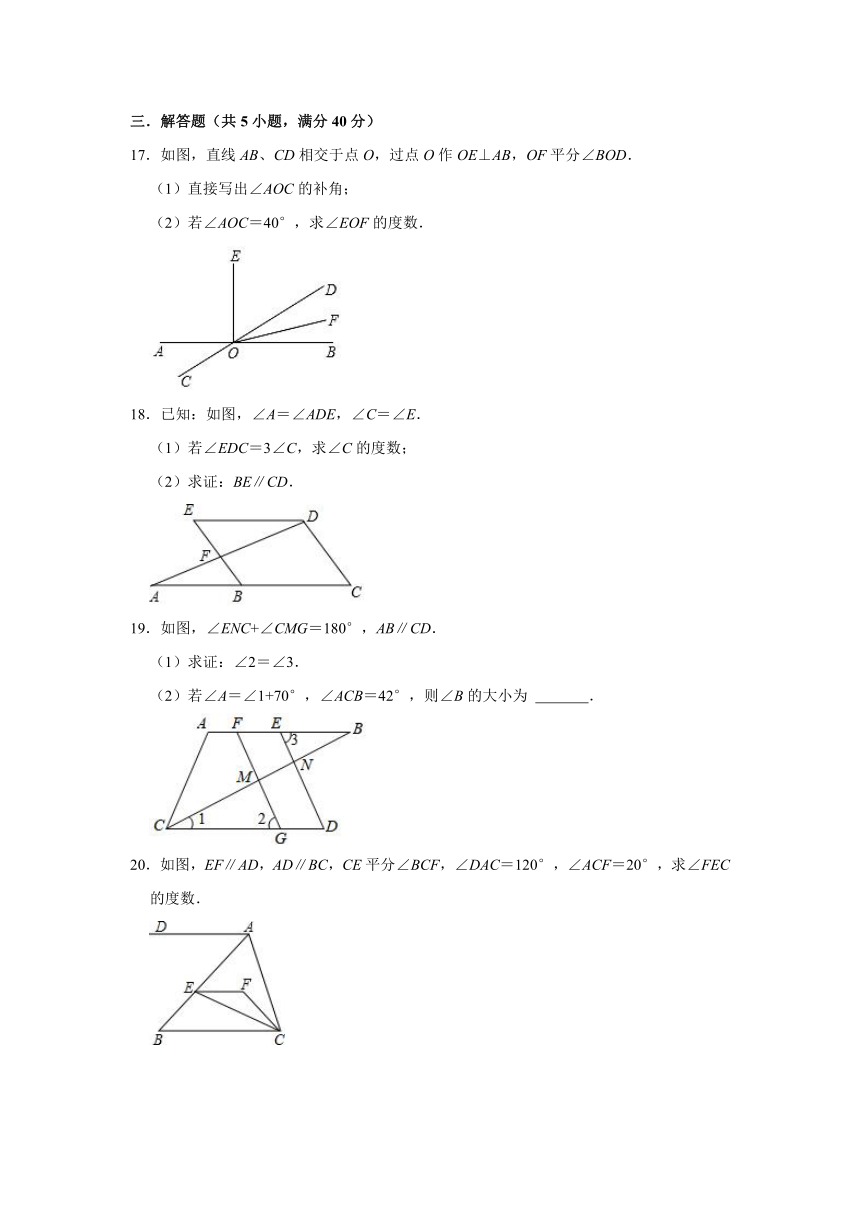
文档简介
2021-2022学年冀教版七年级数学下册《第7章相交线与平行线》单元综合测试题(附答案)
一.选择题(共8小题,满分40分)
1.在下面四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
2.下列画图语句中,正确的是( )
A.画射线OP=3cm B.画出A、B两点的距离
C.延长射线OA D.连接A、B两点
3.如图,给出下列说法:①∠B和∠1是同位角;②∠1和∠3是对顶角;③∠2和∠4是内错角;④∠A和∠BCD是同旁内角.其中说法正确的有( )
A.0个 B.1个 C.2个 D.3个
4.若点A到直线l的距离为7cm,点B到直线l的距离为3cm,则线段AB的长度为( )
A.10cm B.4cm C.10cm或4cm D.至少4cm
5.观察如图,并阅读图形下面的相关文字:
两条直线相交,最多有1个交点;三条直线相交,最多有3个交点;4条直线相交,最多有6个交点……
像这样,20条直线相交,交点最多的个数是( )
A.100个 B.135个 C.190个 D.200个
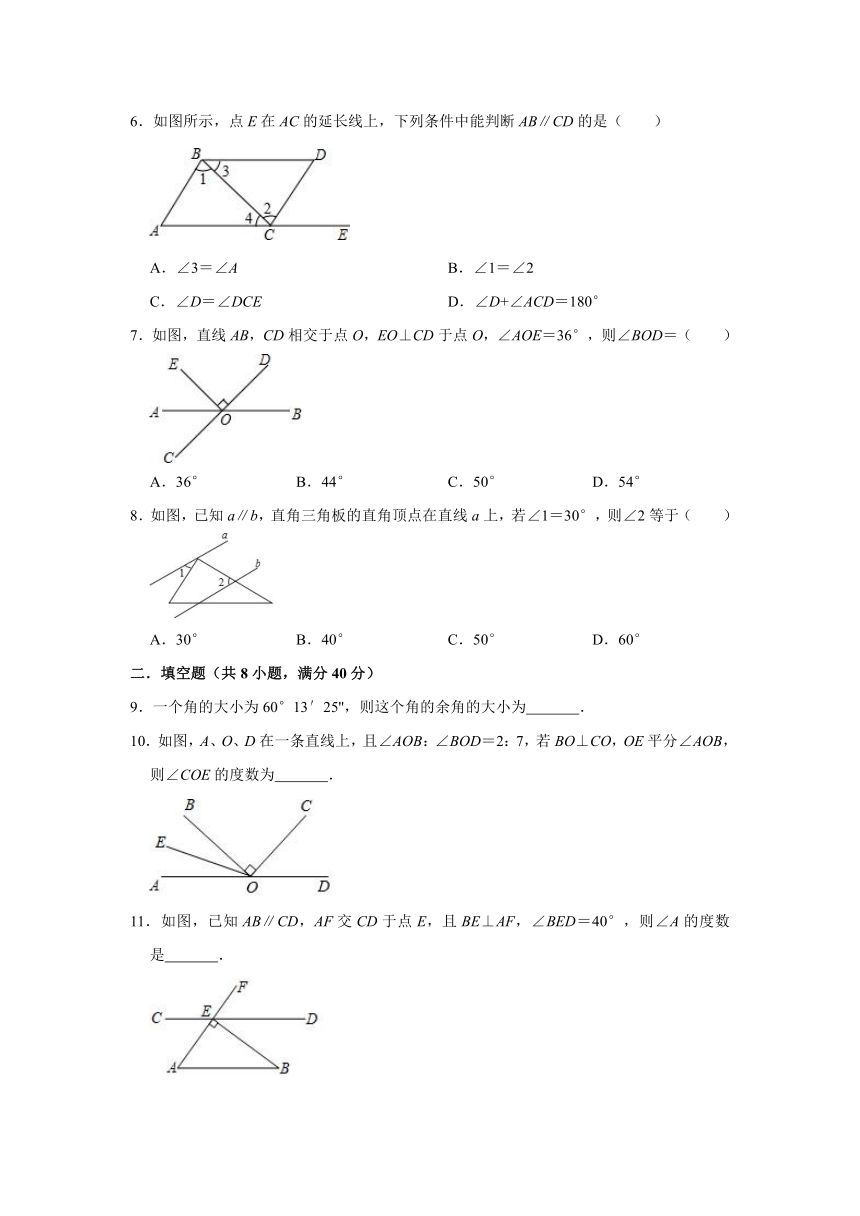
6.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A B.∠1=∠2
C.∠D=∠DCE D.∠D+∠ACD=180°
7.如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )
A.36° B.44° C.50° D.54°
8.如图,已知a∥b,直角三角板的直角顶点在直线a上,若∠1=30°,则∠2等于( )
A.30° B.40° C.50° D.60°
二.填空题(共8小题,满分40分)
9.一个角的大小为60°13′25'',则这个角的余角的大小为 .
10.如图,A、O、D在一条直线上,且∠AOB:∠BOD=2:7,若BO⊥CO,OE平分∠AOB,则∠COE的度数为 .
11.如图,已知AB∥CD,AF交CD于点E,且BE⊥AF,∠BED=40°,则∠A的度数是 .
12.把一块直尺与一块直角三角板如图放置,若∠1=38°,则∠2的度数为 .
13.如图,AB∥CD,∠A=75°,∠C=30°,∠E的度数为 .
14.如图所示,AB∥DE,∠1=130°,∠2=36°,则∠3= 度.
15.如图,AB∥CD,Rt△EFG的直角顶点E在直线AB上,且EF交CD于点P,若∠BEG=52°,则∠CPF的度数为 .
16.如图,AB∥EF,C点在EF上,∠EAC=∠ECA,BC平分∠DCF,且AC平分∠DCE.下列结论中正确的是 .
A.AC⊥BC
B.AE∥CD
C.∠1+∠B=90°
D.∠BDC=2∠1
三.解答题(共5小题,满分40分)
17.如图,直线AB、CD相交于点O,过点O作OE⊥AB,OF平分∠BOD.
(1)直接写出∠AOC的补角;
(2)若∠AOC=40°,求∠EOF的度数.
18.已知:如图,∠A=∠ADE,∠C=∠E.
(1)若∠EDC=3∠C,求∠C的度数;
(2)求证:BE∥CD.
19.如图,∠ENC+∠CMG=180°,AB∥CD.
(1)求证:∠2=∠3.
(2)若∠A=∠1+70°,∠ACB=42°,则∠B的大小为 .
20.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
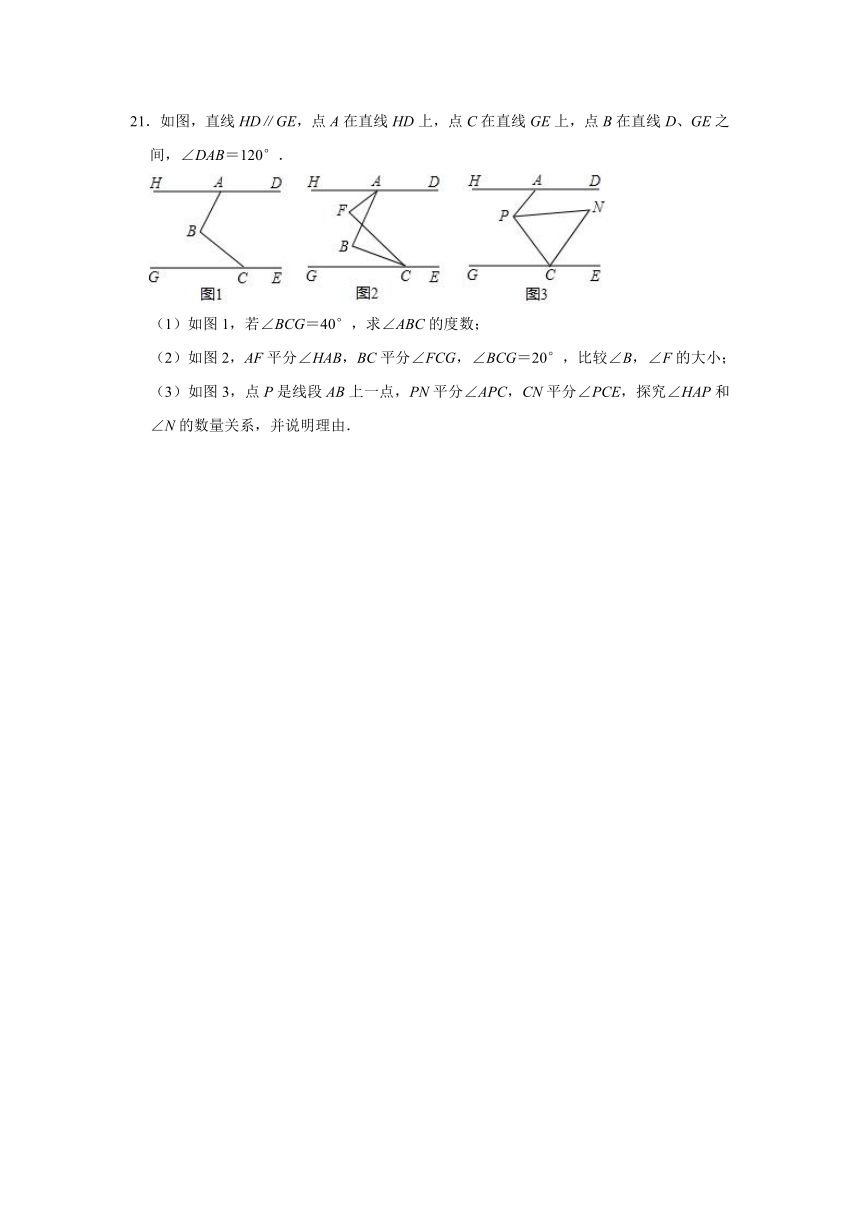
21.如图,直线HD∥GE,点A在直线HD上,点C在直线GE上,点B在直线D、GE之间,∠DAB=120°.
(1)如图1,若∠BCG=40°,求∠ABC的度数;
(2)如图2,AF平分∠HAB,BC平分∠FCG,∠BCG=20°,比较∠B,∠F的大小;
(3)如图3,点P是线段AB上一点,PN平分∠APC,CN平分∠PCE,探究∠HAP和∠N的数量关系,并说明理由.
参考答案
一.选择题(共8小题,满分40分)
1.解:A、∠1与∠2不是对顶角;
B、∠1与∠2是对顶角;
C、∠1与∠2不是对顶角;
D、∠1与∠2不是对顶角;
故选:B.
2.解:A、射线OP无限长,所以A选项不符合题意;
B、量出A、B点的距离,所以B选项不符合题意;
C、射线OA不需要延长,只能反向延长射线OA,所以C选项不符合题意;
D、用直尺可以连接A、B两点,所以D选项符合题意.
故选:D.
3.解:如图所示,①∠B和∠1是同旁内角,故说法错误;
②∠1和∠3不是对顶角,故说法错误;
③∠2和∠4是内错角,故说法正确;
④∠A和∠BCD不是同旁内角,故说法错误.
综上所述,说法正确的结论有1个.
故选:B.
4.解:从点A作直线l的垂线,垂足为C点,当A、B、C三点共线时,线段AB的长为7﹣3=4cm,其它情况下大于4cm,
当A、B在直线l的两侧时,AB>4cm,
故选:D.
5.解:2条直线相交最多有1个交点,1=×1×2,
3条直线相交最多有3个交点,3=1+2=×2×3,
4条直线相交最多有6个交点,6=1+2+3=×3×4,
5条直线相交最多有10个交点,10=1+2+3+4=×4×5,…
n条直线相交最多有交点的个数是:n(n﹣1).
20条直线相交最多有交点的个数是:n(n﹣1)=×20×19=190.
故选:C.
6.解:A、∠3=∠A,无法得到,AB∥CD,故此选项错误;
B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项正确;
C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项错误;
D、∠D+∠ACD=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项错误;
故选:B.
7.解:∵EO⊥CD,
∴∠EOD=90°,
又∵∠AOE+∠EOD+∠BOD=180°,∠AOE=36°,
∴∠BOD=54°,
故选:D.
8.解:∵直角三角板的直角顶点在直线a上,∠1=30°,
∴∠3=60°,
∵a∥b,
∴∠2=∠3=60°,
故选:D.
二.填空题(共8小题,满分40分)
9.解:根据余角的定义:若一个角是60°13′25'',
则这个角的余角的大小为90°﹣60°13′25''=29°46'35''.
故答案为29°46'35''.
10.解:∵∠BOE=××180°=20°,∠BOC=90°,
∴∠COE的度数为:90°+20°=110°,
故答案为:110°.
11.解:∵AB∥CD,
∴∠B=∠BED=40°.
∵BE⊥AF,
∴∠AEB=90°,
∴∠A=180°﹣∠AEB﹣∠B=180°﹣90°﹣40°=50°.
故答案为:50°.
12.解:如图,
∵∠1=∠3=38°,
∴∠2=90°+∠3=90°+38°=128°.
故答案为:128°.
13.解:过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,EF∥CD,
∴∠AEF=∠A=75°,∠CEF=∠C=30°,
∴∠AEC=∠AEF﹣∠CEF=75°﹣30°=45°.
故答案为:45°.
14.解:过点C作CM∥AB,则CM∥DE,
∵CM∥DE,∠2=36°,
∴∠MCD=∠2=36°,
∵AB∥CM,∠1=130°,
∴∠MCB+∠1=180°,
∴∠MCB=50°;
∴∠BCD=∠MCB+∠MCD=50°+36°=86°.
故答案为:86.
15.解:∵∠BEG=52°,∠GEF=90°,
∴∠AEF=180°﹣∠GEF﹣∠BEG=38°,
∵AB∥CD,
∴∠CPF=∠AEF=38°,
故答案为:38°.
16.解:∵BC平分∠DCF,且AC平分∠DCE,
∴∠FCB=∠DCB=∠FCD,∠ECA=∠1=∠ECD,
∵∠ECD+∠FCD=180°,
∴∠1+∠DCB=×180°=90°=∠ACB,
∴AC⊥BC,
故①正确,符合题意;
∵AC平分∠DCE,
∴∠1=∠ECA,
∵∠EAC=∠ECA,
∴∠1=∠EAC,
∴AE∥CD,
故②正确,符合题意;
∵AC⊥BC,
∴∠1+∠DCB=90°,
∵BC平分∠DCF,
∴∠FCB=∠DCB,
∴∠1+∠FCB=90°,
∵AB∥EF,
∴∠B=∠FCB,
∴∠1+∠B=90°,
故③正确,符合题意;
∵AC平分∠DCE,
∴∠1=∠ECA,
∵AB∥EF,
∴∠ECA=∠CAD,
∴∠1=∠CAD,
∴∠BDC=∠1+∠CAD=2∠1,
故④正确,符合题意.
故选:ABCD.
三.解答题(共5小题,满分40分)
17.解:(1)∠AOC的补角是∠AOD,∠BOC;
(2)∵∠AOC=40°,
∴∠BOD=∠AOC=40°,
∵OF平分∠BOD,
∴∠BOF=20°,
∵OE⊥AB,
∴∠EOB=90°,
∴∠EOF=90°﹣20°=70°.
18.解:(1)∵∠A=∠ADE,
∴AC∥DE,
∴∠EDC+∠C=180°,
又∵∠EDC=3∠C,
∴4∠C=180°,
即∠C=45°;
(2)∵AC∥DE,
∴∠E=∠ABE,
又∵∠C=∠E,
∴∠C=∠ABE,
∴BE∥CD.
19.(1)证明:∵∠ENC+∠CMG=180°,∠FMB=∠CMG,
∴∠ENC+∠ENC=180°,
∴DE∥FG,
∴∠3=∠BFG,
∵AB∥CD,
∴∠BFG=∠2,
∴∠2=∠3;
(2)解:∵AB∥CD,
∴∠A+∠ACD=180°,∠1=∠B,
∵∠A=∠1+70°,∠ACB=42°,
∴∠1+70°+∠ACB+∠1=180°,
即∠1+70°+42°+∠1=180°,
解得:∠1=34°,
∴∠B=∠1=34°.
故答案为:34°.
20.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
21.解:(1)过点B作BM∥HD,则HD∥GE∥BM,如图1,
∴∠ABM=180°﹣∠DAB,∠CBM=∠BCG,
∵∠DAB=120°,∠BCG=40°,
∴∠ABM=60°,∠CBM=40°,
∴∠ABC=∠ABM+∠CBM=100°;
(2)过B作BP∥HD∥GE,过F作FQ∥HD∥GE,如图2,
∴∠ABP=∠HAB,∠CBP=∠BCG,∠AFQ=∠HAF,∠CFQ=∠FCG,
∴∠ABC=∠HAB+∠BCG,∠AFC=∠HAF+∠FCG,
∵∠DAB=120°,
∴∠HAB=180°﹣120°=60°,
∵AF平分∠HAB,BC平分∠FCG,∠BCG=20°,
∴∠HAF=30°,∠FCG=40°,
∴∠ABC=60°+20°=80°,
∠AFC=30°+40°=70°,
∴∠ABC>∠AFC;
(3)过P作PK∥HD∥GE,如图3,
∴∠APK=∠HAP,∠CPK=∠PCG,
∴∠APC=∠HAP+∠PCG,
∵PN平分∠APC,
∴∠NPC=∠HAP+∠PCG,
∵∠PCE=180°﹣∠PCG,CN平分∠PCE,
∴∠PCN==90°﹣∠PCG,
∵∠N+∠NPC+∠PCN=180°,
∴∠N=180°﹣∠HAP﹣∠PCG﹣90°+∠PCG=90°﹣∠HAP,
即,∠N=90°﹣∠HAP.
一.选择题(共8小题,满分40分)
1.在下面四个图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
2.下列画图语句中,正确的是( )
A.画射线OP=3cm B.画出A、B两点的距离
C.延长射线OA D.连接A、B两点
3.如图,给出下列说法:①∠B和∠1是同位角;②∠1和∠3是对顶角;③∠2和∠4是内错角;④∠A和∠BCD是同旁内角.其中说法正确的有( )
A.0个 B.1个 C.2个 D.3个
4.若点A到直线l的距离为7cm,点B到直线l的距离为3cm,则线段AB的长度为( )
A.10cm B.4cm C.10cm或4cm D.至少4cm
5.观察如图,并阅读图形下面的相关文字:
两条直线相交,最多有1个交点;三条直线相交,最多有3个交点;4条直线相交,最多有6个交点……
像这样,20条直线相交,交点最多的个数是( )
A.100个 B.135个 C.190个 D.200个
6.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A B.∠1=∠2
C.∠D=∠DCE D.∠D+∠ACD=180°
7.如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )
A.36° B.44° C.50° D.54°
8.如图,已知a∥b,直角三角板的直角顶点在直线a上,若∠1=30°,则∠2等于( )
A.30° B.40° C.50° D.60°
二.填空题(共8小题,满分40分)
9.一个角的大小为60°13′25'',则这个角的余角的大小为 .
10.如图,A、O、D在一条直线上,且∠AOB:∠BOD=2:7,若BO⊥CO,OE平分∠AOB,则∠COE的度数为 .
11.如图,已知AB∥CD,AF交CD于点E,且BE⊥AF,∠BED=40°,则∠A的度数是 .
12.把一块直尺与一块直角三角板如图放置,若∠1=38°,则∠2的度数为 .
13.如图,AB∥CD,∠A=75°,∠C=30°,∠E的度数为 .
14.如图所示,AB∥DE,∠1=130°,∠2=36°,则∠3= 度.
15.如图,AB∥CD,Rt△EFG的直角顶点E在直线AB上,且EF交CD于点P,若∠BEG=52°,则∠CPF的度数为 .
16.如图,AB∥EF,C点在EF上,∠EAC=∠ECA,BC平分∠DCF,且AC平分∠DCE.下列结论中正确的是 .
A.AC⊥BC
B.AE∥CD
C.∠1+∠B=90°
D.∠BDC=2∠1
三.解答题(共5小题,满分40分)
17.如图,直线AB、CD相交于点O,过点O作OE⊥AB,OF平分∠BOD.
(1)直接写出∠AOC的补角;
(2)若∠AOC=40°,求∠EOF的度数.
18.已知:如图,∠A=∠ADE,∠C=∠E.
(1)若∠EDC=3∠C,求∠C的度数;
(2)求证:BE∥CD.
19.如图,∠ENC+∠CMG=180°,AB∥CD.
(1)求证:∠2=∠3.
(2)若∠A=∠1+70°,∠ACB=42°,则∠B的大小为 .
20.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
21.如图,直线HD∥GE,点A在直线HD上,点C在直线GE上,点B在直线D、GE之间,∠DAB=120°.
(1)如图1,若∠BCG=40°,求∠ABC的度数;
(2)如图2,AF平分∠HAB,BC平分∠FCG,∠BCG=20°,比较∠B,∠F的大小;
(3)如图3,点P是线段AB上一点,PN平分∠APC,CN平分∠PCE,探究∠HAP和∠N的数量关系,并说明理由.
参考答案
一.选择题(共8小题,满分40分)
1.解:A、∠1与∠2不是对顶角;
B、∠1与∠2是对顶角;
C、∠1与∠2不是对顶角;
D、∠1与∠2不是对顶角;
故选:B.
2.解:A、射线OP无限长,所以A选项不符合题意;
B、量出A、B点的距离,所以B选项不符合题意;
C、射线OA不需要延长,只能反向延长射线OA,所以C选项不符合题意;
D、用直尺可以连接A、B两点,所以D选项符合题意.
故选:D.
3.解:如图所示,①∠B和∠1是同旁内角,故说法错误;
②∠1和∠3不是对顶角,故说法错误;
③∠2和∠4是内错角,故说法正确;
④∠A和∠BCD不是同旁内角,故说法错误.
综上所述,说法正确的结论有1个.
故选:B.
4.解:从点A作直线l的垂线,垂足为C点,当A、B、C三点共线时,线段AB的长为7﹣3=4cm,其它情况下大于4cm,
当A、B在直线l的两侧时,AB>4cm,
故选:D.
5.解:2条直线相交最多有1个交点,1=×1×2,
3条直线相交最多有3个交点,3=1+2=×2×3,
4条直线相交最多有6个交点,6=1+2+3=×3×4,
5条直线相交最多有10个交点,10=1+2+3+4=×4×5,…
n条直线相交最多有交点的个数是:n(n﹣1).
20条直线相交最多有交点的个数是:n(n﹣1)=×20×19=190.
故选:C.
6.解:A、∠3=∠A,无法得到,AB∥CD,故此选项错误;
B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项正确;
C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项错误;
D、∠D+∠ACD=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项错误;
故选:B.
7.解:∵EO⊥CD,
∴∠EOD=90°,
又∵∠AOE+∠EOD+∠BOD=180°,∠AOE=36°,
∴∠BOD=54°,
故选:D.
8.解:∵直角三角板的直角顶点在直线a上,∠1=30°,
∴∠3=60°,
∵a∥b,
∴∠2=∠3=60°,
故选:D.
二.填空题(共8小题,满分40分)
9.解:根据余角的定义:若一个角是60°13′25'',
则这个角的余角的大小为90°﹣60°13′25''=29°46'35''.
故答案为29°46'35''.
10.解:∵∠BOE=××180°=20°,∠BOC=90°,
∴∠COE的度数为:90°+20°=110°,
故答案为:110°.
11.解:∵AB∥CD,
∴∠B=∠BED=40°.
∵BE⊥AF,
∴∠AEB=90°,
∴∠A=180°﹣∠AEB﹣∠B=180°﹣90°﹣40°=50°.
故答案为:50°.
12.解:如图,
∵∠1=∠3=38°,
∴∠2=90°+∠3=90°+38°=128°.
故答案为:128°.
13.解:过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,EF∥CD,
∴∠AEF=∠A=75°,∠CEF=∠C=30°,
∴∠AEC=∠AEF﹣∠CEF=75°﹣30°=45°.
故答案为:45°.
14.解:过点C作CM∥AB,则CM∥DE,
∵CM∥DE,∠2=36°,
∴∠MCD=∠2=36°,
∵AB∥CM,∠1=130°,
∴∠MCB+∠1=180°,
∴∠MCB=50°;
∴∠BCD=∠MCB+∠MCD=50°+36°=86°.
故答案为:86.
15.解:∵∠BEG=52°,∠GEF=90°,
∴∠AEF=180°﹣∠GEF﹣∠BEG=38°,
∵AB∥CD,
∴∠CPF=∠AEF=38°,
故答案为:38°.
16.解:∵BC平分∠DCF,且AC平分∠DCE,
∴∠FCB=∠DCB=∠FCD,∠ECA=∠1=∠ECD,
∵∠ECD+∠FCD=180°,
∴∠1+∠DCB=×180°=90°=∠ACB,
∴AC⊥BC,
故①正确,符合题意;
∵AC平分∠DCE,
∴∠1=∠ECA,
∵∠EAC=∠ECA,
∴∠1=∠EAC,
∴AE∥CD,
故②正确,符合题意;
∵AC⊥BC,
∴∠1+∠DCB=90°,
∵BC平分∠DCF,
∴∠FCB=∠DCB,
∴∠1+∠FCB=90°,
∵AB∥EF,
∴∠B=∠FCB,
∴∠1+∠B=90°,
故③正确,符合题意;
∵AC平分∠DCE,
∴∠1=∠ECA,
∵AB∥EF,
∴∠ECA=∠CAD,
∴∠1=∠CAD,
∴∠BDC=∠1+∠CAD=2∠1,
故④正确,符合题意.
故选:ABCD.
三.解答题(共5小题,满分40分)
17.解:(1)∠AOC的补角是∠AOD,∠BOC;
(2)∵∠AOC=40°,
∴∠BOD=∠AOC=40°,
∵OF平分∠BOD,
∴∠BOF=20°,
∵OE⊥AB,
∴∠EOB=90°,
∴∠EOF=90°﹣20°=70°.
18.解:(1)∵∠A=∠ADE,
∴AC∥DE,
∴∠EDC+∠C=180°,
又∵∠EDC=3∠C,
∴4∠C=180°,
即∠C=45°;
(2)∵AC∥DE,
∴∠E=∠ABE,
又∵∠C=∠E,
∴∠C=∠ABE,
∴BE∥CD.
19.(1)证明:∵∠ENC+∠CMG=180°,∠FMB=∠CMG,
∴∠ENC+∠ENC=180°,
∴DE∥FG,
∴∠3=∠BFG,
∵AB∥CD,
∴∠BFG=∠2,
∴∠2=∠3;
(2)解:∵AB∥CD,
∴∠A+∠ACD=180°,∠1=∠B,
∵∠A=∠1+70°,∠ACB=42°,
∴∠1+70°+∠ACB+∠1=180°,
即∠1+70°+42°+∠1=180°,
解得:∠1=34°,
∴∠B=∠1=34°.
故答案为:34°.
20.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
21.解:(1)过点B作BM∥HD,则HD∥GE∥BM,如图1,
∴∠ABM=180°﹣∠DAB,∠CBM=∠BCG,
∵∠DAB=120°,∠BCG=40°,
∴∠ABM=60°,∠CBM=40°,
∴∠ABC=∠ABM+∠CBM=100°;
(2)过B作BP∥HD∥GE,过F作FQ∥HD∥GE,如图2,
∴∠ABP=∠HAB,∠CBP=∠BCG,∠AFQ=∠HAF,∠CFQ=∠FCG,
∴∠ABC=∠HAB+∠BCG,∠AFC=∠HAF+∠FCG,
∵∠DAB=120°,
∴∠HAB=180°﹣120°=60°,
∵AF平分∠HAB,BC平分∠FCG,∠BCG=20°,
∴∠HAF=30°,∠FCG=40°,
∴∠ABC=60°+20°=80°,
∠AFC=30°+40°=70°,
∴∠ABC>∠AFC;
(3)过P作PK∥HD∥GE,如图3,
∴∠APK=∠HAP,∠CPK=∠PCG,
∴∠APC=∠HAP+∠PCG,
∵PN平分∠APC,
∴∠NPC=∠HAP+∠PCG,
∵∠PCE=180°﹣∠PCG,CN平分∠PCE,
∴∠PCN==90°﹣∠PCG,
∵∠N+∠NPC+∠PCN=180°,
∴∠N=180°﹣∠HAP﹣∠PCG﹣90°+∠PCG=90°﹣∠HAP,
即,∠N=90°﹣∠HAP.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
