人教版五年级数学下册 正方体的认识精选练习题目(有答案)
文档属性
| 名称 | 人教版五年级数学下册 正方体的认识精选练习题目(有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
五年级下册-正方体的认识精选练习题目
学校:___________ 姓名:___________ 班级:___________ 学号:___________
一、正方体的特征
1.长方体( )的面完全相同,正方体( )的面完全相同。
2.正方体和长方体都有________个面,________个顶点,________条棱。
3.一个正方体,无论从前面、上面或左面,看到的都是( )形。
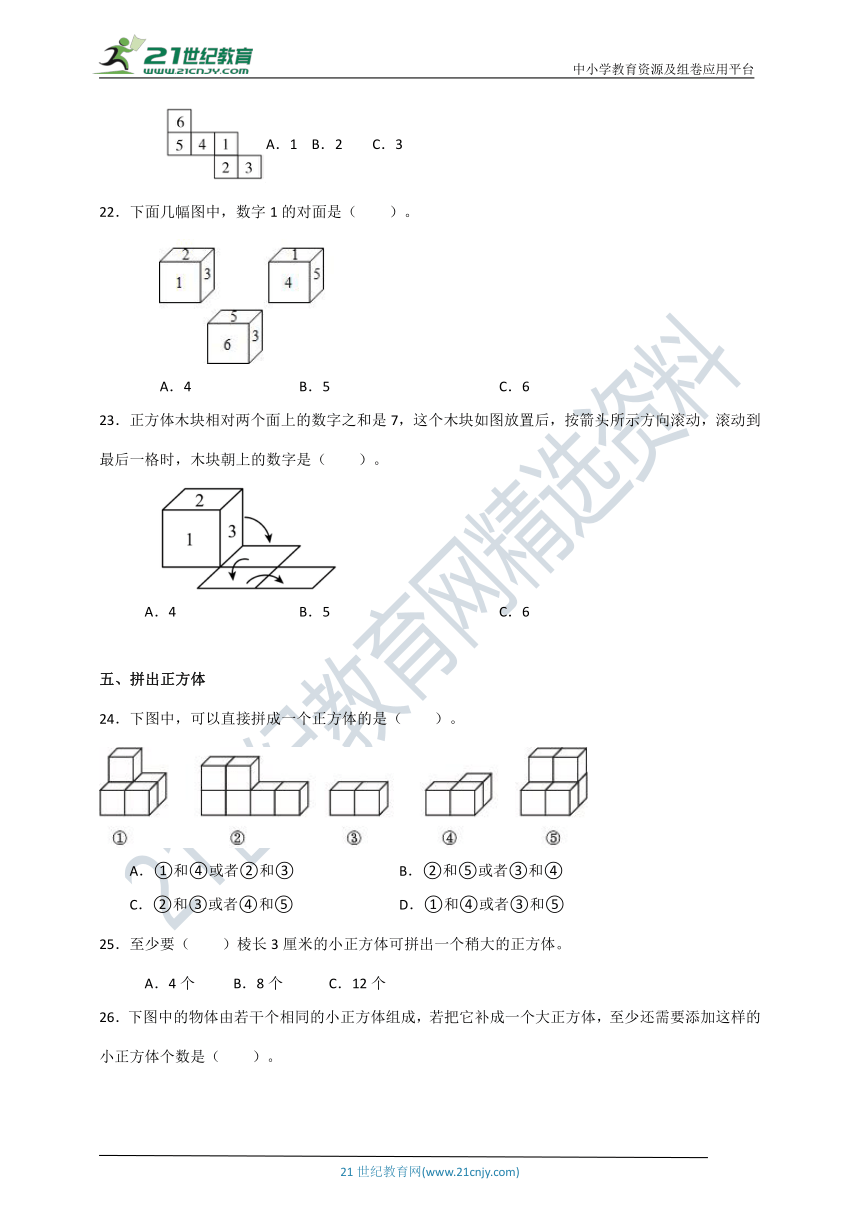
4.下图中,用小棒与小球搭一个正方体,还缺( )个小球和( )根小棒。
5.如图,这个魔方是( )体,它的棱长是( )cm,有( )个面的形状完全相同。
6.每个长方体或正方体,棱的数量都是( )。
A.4条 B.6条 C.8条 D.12条
7.下面几种纸片,请你从中选出5张,围一个无盖的长方体或正方体。
下面第( )种围法,体积最大。
A.①②②③③ B.③③③③④ C.②②②③③ D.5张④
二、判断题
8.用至少4个相同的小正方体才能拼成一个大正方体。( )
9.观察正方体时,从正面和左面看到的形状完全相同。( )
10.四个正方体可以组成一个大的正方体。( )
11.有三条棱相交于一个顶点,且长度相等的长方体一定是正方体。( )
12.长方体是特殊的正方体. ( )
三、棱长总和
13.一个正方体的底面周长是12cm,它的棱长之和是( )cm。
14.若一个正方体棱和扩大到原来的2倍,则这个正方体的棱长总和扩大到原来的( )倍。
A.2 B.8 C.12 D.24
15.如下图,绳子的长是( )厘米。
16.捆下图正方体盒子要用( )厘米彩带。(打结用了35厘米彩带)
17.一个正方体的棱长总和是60cm,它的棱长是( ).
A.4cm B.5cm C.10cm
18.现在有一根150cm长的铁丝,用这根铁丝焊成了一个正方体的框架,还剩铁丝6cm。这个正方体框架的棱长是________厘米。
19.用一根铁丝制成了一个长8cm,宽8cm,高是2cm的长方体框架.如果用这根铁丝制成一个正方体,制成的正方体的棱长是多少厘米?
四、展开图
20.下列图形中,不能折成正方体的图形是( )
A. B. C. D.
21.如图为一个正方体盒子的展开图,与4号面对的面是( )号面。
A.1 B.2 C.3
22.下面几幅图中,数字1的对面是( )。
A.4 B.5 C.6
23.正方体木块相对两个面上的数字之和是7,这个木块如图放置后,按箭头所示方向滚动,滚动到最后一格时,木块朝上的数字是( )。
A.4 B.5 C.6
五、拼出正方体
24.下图中,可以直接拼成一个正方体的是( )。
①和④或者②和③ B.②和⑤或者③和④
C.②和③或者④和⑤ D.①和④或者③和⑤
25.至少要( )棱长3厘米的小正方体可拼出一个稍大的正方体。
A.4个 B.8个 C.12个
26.下图中的物体由若干个相同的小正方体组成,若把它补成一个大正方体,至少还需要添加这样的小正方体个数是( )。
A.9 B.14 C.16
27.至少用( )个同样的正方体才能拼成一个新的正方体。
A.4 B.8 C.16 D.27
28.如图是用小正方体搭成一个立体图形,它是由( )块小正方体搭成的。
A.6 B.9 C.10
29.一个长方体长、宽、高,把它切成一个尽可能大的正方体,这个正方体的棱长是( )。
A.12 B.9 C.8 D.7
30.乐乐把若干个白色小正方体木块拼成如图所示的大的正方体,然后在它的表面涂上颜色。
(1)2个面被涂色的小正方体木块有( )块。
(2)1个面被涂色的小正方体木块有( )块。
没有被涂色的小正方体木块有( )块。
参考答案:
1. 相对 所有
【分析】长方体中每两个相对的面完全相同,在一个长方体中最多有4个面完全相同;正方体有6个面,所有的面完全相同,据此解答。
【详解】长方体( 相对 )的面完全相同,正方体( 所有 )的面完全相同。
【点睛】掌握长方体和正方体的特征是解答题目的关键。
2. 6 8 12
【解析】正方体和长方体都有6个面,正方体是正方形的面,长方体至少有4个长方形的面;长方体和正方体都有8个顶点;长方体和正方体都有12条棱,正方体所有棱的长度相等,长方体相对的棱长度相等。
【详解】正方体和长方体都有6个面,8个顶点,12条棱。
故答案为:6;8;12。
【点睛】本题考查了正方体和长方体的特征,正方体可以看成特殊的长方体。
3.正方
【解析】从正面看正方体,看到的是正方体的前面;从上面看正方体,看到的是正方体的上面;从左面或右面看正方体,看到的是正方体的侧面;根据正方体的特征可知,正方体的每个面都是相同的正方形;因此可以判断:一个正方体,不论从正面、上面、侧面看都是正方形。
【详解】根据分析可知,一个正方体,无论从前面、上面或左面,看到的都是正方形。
【点睛】本题考查了从不同方向观察物体和几何体,关键是理解正方体的特征。
4. 1 5
5. 正方 10 6
【分析】根据正方体的特征解答,正方体有6个面,每个面完全相同。有8个顶点,有12条棱,每条棱长度相等。
【详解】这个魔方是正方体,它的棱长是10cm,有6个面的形状完全相同。
【点睛】掌握正方体的特征是解题的关键。
6.D
【解析】不论是长方体还是正方体,都有6个面,8个顶点,12条棱,据此进行判断。
【详解】每个长方体或正方体,棱的数量都是12条;故答案选:D。
【点睛】本题考查的是长方体和正方体的基本特征,长方体有4条长,4条宽,4条高,正方体的12条棱都相等。
7.A
【解析】根据长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,计算出长方体或正方体的体积,比较即可。
【详解】A. ①②②③③,长方体的长、宽、高分别是5分米、4分米、3分米,体积是5×4×3=20×3=60(立方分米);
B.③③③③④,长方体的长、宽、高分别是3分米、3分米、4分米,体积3×3×4=9×4=36(立方分米)
C.②②②③③,无法围成长方体或正方体。
D. 5张④,正方体的棱长是3分米,体积是3×3×3=9×3=27(立方分米)
60>36>27
故选择:A
【点睛】此题考查了长方体、正方体的特征以及体积计算,根据所给选项先确定出长方体的长、宽、高是解题关键。
8.×
【解析】正方体的12条棱长度相等,用4个相同的小正方体拼成的是一个长方形,要拼成一个较大的正方体至少需要8个相同的小正方体,据此解答。
【详解】
由图可知,4个相同的小正方体拼成的是长方体,用至少8个相同的小正方体才能拼成一个大正方体。
故答案为:×
【点睛】掌握正方体的特征是解答题目的关键。
9.√
【解析】根据正方体特征,正方体有6个面,都是完全一样的正方形,进行分析。
10.×
【解析】小正方体拼组大正方体,每条棱长上至少需要2个小正方体,由此即可求得小正方体的个数。
【详解】
2×2×2=8(个)
所以至少需要8个小正方体才能拼成一个大正方体,原题说法错误。
故答案为:×。
【点睛】本题主要考查正方体的特征(12条棱长度都相等)。
11.√
【分析】
正方体的棱的特点是每条棱的长度都相等,据此进行判断即可。
【详解】
三条棱相交于一个顶点,且长度相等,说明这个长方体的长、宽、高长度都相等,则每条棱长度都相等,它是正方体,原题说法正确;
故答案为:√。
【点睛】
熟练掌握正方体的特征是解答本题的关键。
12.×
【解析】长、宽、高都相等的长方体叫做正方体,正方体是特殊的长方体,也叫立方体,据此判断.
13.36
【解析】根据正方体的特征,12条棱的长度都相等,6个面的面积都相等.已知一个正方体的底面周长是12厘米,根据正方形的周长公式:,用周长除以4求出边长,再根据正方体的棱长总和=棱长×12,由此列式解答。
【详解】
12÷4=3(厘米)
3×12=36(厘米)
【点睛】此题主要考查正方体的特征和棱长总和的计算,根据求棱长总和的公式,直接列式解答。
14.A
【解析】根据正方体的棱长总和=棱长×12,举例计算即可。
【详解】设一个正方体棱长原来是1,则棱长总和是1×12=12;
一个正方体棱长扩大到原来的2倍就是2,则棱长总和是2×12=24。
则这个正方体的棱长总和扩大到原来的2倍。
故选:A。
【点睛】掌握正方体的棱长总和公式是关键。
15.340
【解析】绳长为30×4+60×2+40×2+20=340(厘米)
16.355
【解析】观察图形可知,所用彩带的长度相当于两个边长是40厘米的正方形的周长和加上35厘米;据此根据正方形周长计算公式即可解题。
【详解】
40×4×2+35
=160×2+35
=320+35
=355(厘米)
所以,捆下图正方体盒子要用355厘米彩带。(打结用了35厘米彩带)
【点睛】熟记:正方形周长=边长×4,是解答此题的关键。
17.B
【解析】正方体的棱长之和=棱长×12,用60除以12,求出棱长,列式解答即可.
【详解】
60÷12=5(厘米) 答:它的棱长是5厘米.
故选B.
18.12
【解析】用150-6求出正方体的棱长总和,再根据正方体有12条棱,而且每条棱都相等可知,正方体的棱长总和除以12等于每一条棱的棱长。
【详解】
(150-6)÷12=144÷12=12(cm)
【点睛】解答本题的关键是先求出正方体的棱长总和。
19.6厘米
【解析】(8×8+2×4)÷12=72÷12=6(厘米)
或(8×4+8×4+2×4)÷12
20.A
【解析】A、折叠后有一个面重合,缺少一个底面,故不能折成正方体;
B、C、D都可以折成正方体.
故选A.
21.C
【解析】确定一个面,以一个面为底面,依次确定其它面的位置,如确定4号面为底面,找到上面即可。
【详解】
以4号面为底面,1号面为右面,2号面为前面,则3号面为上面,所以与4号面对的面是3号面。
故答案为:C
【点睛】关键是熟悉正方体特征,具有一定的空间想象能力。
22.C
【解析】根据图形判断数字1的相邻面,和数字1相邻的面一定不是数字1的相对面,最后排除数字1的相邻面即可得到数字1的相对面。
【详解】
由可知,数字2和数字3是数字1的相邻面,由可知,数字4和数字5是数字1的相邻面,数字2、3、4、5一定不是数字1的相对面,由可知,数字1的对面是数字6。
故答案为:C
【点睛】
找出数字1的相邻面用排除法得出数字1的相对面是解答题目的关键。
23.B
【解析】由题意可知,1的对面是6,2的对面是5,3的对面是4,第一次滚动后,数字4朝上,1仍朝前;第二次滚动后,1朝下,6朝上;第三次滚动后,2朝下,5朝上。
【详解】1的对面是6,2的对面是5,3的对面是4,第一次滚动后,数字4朝上;第二次滚动后,1朝下,6朝上;第三次滚动后,2朝下,5朝上。
故答案为:B
【点睛】解答此题的关键是根据题意弄清各面上的数字,然后可动手操作一下。
24.D
【解析】观察图可知,①号图形还差3个正方体就可以拼成一个正方体,⑤号图形还差2个正方体就可以拼成一个正方体,据此解答。
【详解】根据题图可知,①和④或者③和⑤可以直接拼成一个正方体。
故答案为:D。
【点睛】解答本题的关键是读懂每个立体图形的特点,进而找到与其相匹配的另一个立体图形。
25.B
【解析】根据正方体的每条棱长度都相等可知,小正方体拼一个稍大的正方体,沿长、宽、高需要各放两个小正方体,一共需要2×2×2=8个,据此解答即可。
【详解】
至少要8个棱长3厘米的小正方体可拼出一个稍大的正方体;
故答案为:B。
【点睛】
熟记正方体的特征是解答本题的关键。
26.B
【解析】根据图形可得,从下向上数,第二层缺1个;第三层缺4个;第四层缺9个;然后相加即可。
【详解】
根据分析可得
1+4+9=14(个)
故答案为:B
【点睛】本题要结合图形的正面观测到的形状,确定各层所缺的小立方体的个数是解答的突破口。
27.B
【解析】要使所用的小正方体最少,那么大正方体的棱长最少可以由2个小正方体的棱长组成,由此即可求得小正方体的个数。
【详解】2×2×2=8(个);故答案为:B。
【点睛】此题考查了小正方体拼组大正方体的特点的灵活应用。
28.C
【解析】如图,最顶层有一个小正方体,第二层有1+2=3(个)小正方体,第三层有1+2+3=6(个)小正方体,则一共有1+3+6=10(个)小正方体。
【详解】结合图示可知:1+3+6=10(个)
故答案为:C。
【点睛】本题需要我们仔细观察图示,通过分析每层的构成规律,来得到每层的小正方体个数,最后把它们相加即可。
29.D
【解析】已知这个长方体长、宽、高,即在长、宽、高这几条线段中,高7厘米是最短的。那么当我们对这个长方体进行切割时,不可能得到棱长是9厘米、或12厘米的正方体,因此,所切割得到的最大的正方体棱长为7厘米。
【详解】由分析得:
7<9<12
所以这个正方体的棱长为7厘米。
故答案为:D。
30. 24 24 8
【解析】观察图形可知,大正方体每条棱上都有4个小正方体,所以小正方体有4×4×4=64块,根据正方体表面积涂色的特点,分别得出切割后小正方体的涂色面的排列特点:
(1)没有涂色的都在内部;
(2)两面涂色的在每条棱上(除去顶点处的小正方体);
(3)一面涂色的都在每一个面上,(除去棱上的小正方体);据此即可解答。
【详解】(1)2个面涂色:(4-2)×12=2×12=24(块)
(2)1个面涂色:4×6=24(块)
(3)没有涂色:(4-2)×(4-2)×(4-2)
=2×2×2
=4×2
=8(块)
【点睛】解答本题的关键是明确;两面涂色的在每条棱长的中间上;一面涂色的在每一个面的中心上;没有涂色的在内部。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
五年级下册-正方体的认识精选练习题目
学校:___________ 姓名:___________ 班级:___________ 学号:___________
一、正方体的特征
1.长方体( )的面完全相同,正方体( )的面完全相同。
2.正方体和长方体都有________个面,________个顶点,________条棱。
3.一个正方体,无论从前面、上面或左面,看到的都是( )形。
4.下图中,用小棒与小球搭一个正方体,还缺( )个小球和( )根小棒。
5.如图,这个魔方是( )体,它的棱长是( )cm,有( )个面的形状完全相同。
6.每个长方体或正方体,棱的数量都是( )。
A.4条 B.6条 C.8条 D.12条
7.下面几种纸片,请你从中选出5张,围一个无盖的长方体或正方体。
下面第( )种围法,体积最大。
A.①②②③③ B.③③③③④ C.②②②③③ D.5张④
二、判断题
8.用至少4个相同的小正方体才能拼成一个大正方体。( )
9.观察正方体时,从正面和左面看到的形状完全相同。( )
10.四个正方体可以组成一个大的正方体。( )
11.有三条棱相交于一个顶点,且长度相等的长方体一定是正方体。( )
12.长方体是特殊的正方体. ( )
三、棱长总和
13.一个正方体的底面周长是12cm,它的棱长之和是( )cm。
14.若一个正方体棱和扩大到原来的2倍,则这个正方体的棱长总和扩大到原来的( )倍。
A.2 B.8 C.12 D.24
15.如下图,绳子的长是( )厘米。
16.捆下图正方体盒子要用( )厘米彩带。(打结用了35厘米彩带)
17.一个正方体的棱长总和是60cm,它的棱长是( ).
A.4cm B.5cm C.10cm
18.现在有一根150cm长的铁丝,用这根铁丝焊成了一个正方体的框架,还剩铁丝6cm。这个正方体框架的棱长是________厘米。
19.用一根铁丝制成了一个长8cm,宽8cm,高是2cm的长方体框架.如果用这根铁丝制成一个正方体,制成的正方体的棱长是多少厘米?
四、展开图
20.下列图形中,不能折成正方体的图形是( )
A. B. C. D.
21.如图为一个正方体盒子的展开图,与4号面对的面是( )号面。
A.1 B.2 C.3
22.下面几幅图中,数字1的对面是( )。
A.4 B.5 C.6
23.正方体木块相对两个面上的数字之和是7,这个木块如图放置后,按箭头所示方向滚动,滚动到最后一格时,木块朝上的数字是( )。
A.4 B.5 C.6
五、拼出正方体
24.下图中,可以直接拼成一个正方体的是( )。
①和④或者②和③ B.②和⑤或者③和④
C.②和③或者④和⑤ D.①和④或者③和⑤
25.至少要( )棱长3厘米的小正方体可拼出一个稍大的正方体。
A.4个 B.8个 C.12个
26.下图中的物体由若干个相同的小正方体组成,若把它补成一个大正方体,至少还需要添加这样的小正方体个数是( )。
A.9 B.14 C.16
27.至少用( )个同样的正方体才能拼成一个新的正方体。
A.4 B.8 C.16 D.27
28.如图是用小正方体搭成一个立体图形,它是由( )块小正方体搭成的。
A.6 B.9 C.10
29.一个长方体长、宽、高,把它切成一个尽可能大的正方体,这个正方体的棱长是( )。
A.12 B.9 C.8 D.7
30.乐乐把若干个白色小正方体木块拼成如图所示的大的正方体,然后在它的表面涂上颜色。
(1)2个面被涂色的小正方体木块有( )块。
(2)1个面被涂色的小正方体木块有( )块。
没有被涂色的小正方体木块有( )块。
参考答案:
1. 相对 所有
【分析】长方体中每两个相对的面完全相同,在一个长方体中最多有4个面完全相同;正方体有6个面,所有的面完全相同,据此解答。
【详解】长方体( 相对 )的面完全相同,正方体( 所有 )的面完全相同。
【点睛】掌握长方体和正方体的特征是解答题目的关键。
2. 6 8 12
【解析】正方体和长方体都有6个面,正方体是正方形的面,长方体至少有4个长方形的面;长方体和正方体都有8个顶点;长方体和正方体都有12条棱,正方体所有棱的长度相等,长方体相对的棱长度相等。
【详解】正方体和长方体都有6个面,8个顶点,12条棱。
故答案为:6;8;12。
【点睛】本题考查了正方体和长方体的特征,正方体可以看成特殊的长方体。
3.正方
【解析】从正面看正方体,看到的是正方体的前面;从上面看正方体,看到的是正方体的上面;从左面或右面看正方体,看到的是正方体的侧面;根据正方体的特征可知,正方体的每个面都是相同的正方形;因此可以判断:一个正方体,不论从正面、上面、侧面看都是正方形。
【详解】根据分析可知,一个正方体,无论从前面、上面或左面,看到的都是正方形。
【点睛】本题考查了从不同方向观察物体和几何体,关键是理解正方体的特征。
4. 1 5
5. 正方 10 6
【分析】根据正方体的特征解答,正方体有6个面,每个面完全相同。有8个顶点,有12条棱,每条棱长度相等。
【详解】这个魔方是正方体,它的棱长是10cm,有6个面的形状完全相同。
【点睛】掌握正方体的特征是解题的关键。
6.D
【解析】不论是长方体还是正方体,都有6个面,8个顶点,12条棱,据此进行判断。
【详解】每个长方体或正方体,棱的数量都是12条;故答案选:D。
【点睛】本题考查的是长方体和正方体的基本特征,长方体有4条长,4条宽,4条高,正方体的12条棱都相等。
7.A
【解析】根据长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,计算出长方体或正方体的体积,比较即可。
【详解】A. ①②②③③,长方体的长、宽、高分别是5分米、4分米、3分米,体积是5×4×3=20×3=60(立方分米);
B.③③③③④,长方体的长、宽、高分别是3分米、3分米、4分米,体积3×3×4=9×4=36(立方分米)
C.②②②③③,无法围成长方体或正方体。
D. 5张④,正方体的棱长是3分米,体积是3×3×3=9×3=27(立方分米)
60>36>27
故选择:A
【点睛】此题考查了长方体、正方体的特征以及体积计算,根据所给选项先确定出长方体的长、宽、高是解题关键。
8.×
【解析】正方体的12条棱长度相等,用4个相同的小正方体拼成的是一个长方形,要拼成一个较大的正方体至少需要8个相同的小正方体,据此解答。
【详解】
由图可知,4个相同的小正方体拼成的是长方体,用至少8个相同的小正方体才能拼成一个大正方体。
故答案为:×
【点睛】掌握正方体的特征是解答题目的关键。
9.√
【解析】根据正方体特征,正方体有6个面,都是完全一样的正方形,进行分析。
10.×
【解析】小正方体拼组大正方体,每条棱长上至少需要2个小正方体,由此即可求得小正方体的个数。
【详解】
2×2×2=8(个)
所以至少需要8个小正方体才能拼成一个大正方体,原题说法错误。
故答案为:×。
【点睛】本题主要考查正方体的特征(12条棱长度都相等)。
11.√
【分析】
正方体的棱的特点是每条棱的长度都相等,据此进行判断即可。
【详解】
三条棱相交于一个顶点,且长度相等,说明这个长方体的长、宽、高长度都相等,则每条棱长度都相等,它是正方体,原题说法正确;
故答案为:√。
【点睛】
熟练掌握正方体的特征是解答本题的关键。
12.×
【解析】长、宽、高都相等的长方体叫做正方体,正方体是特殊的长方体,也叫立方体,据此判断.
13.36
【解析】根据正方体的特征,12条棱的长度都相等,6个面的面积都相等.已知一个正方体的底面周长是12厘米,根据正方形的周长公式:,用周长除以4求出边长,再根据正方体的棱长总和=棱长×12,由此列式解答。
【详解】
12÷4=3(厘米)
3×12=36(厘米)
【点睛】此题主要考查正方体的特征和棱长总和的计算,根据求棱长总和的公式,直接列式解答。
14.A
【解析】根据正方体的棱长总和=棱长×12,举例计算即可。
【详解】设一个正方体棱长原来是1,则棱长总和是1×12=12;
一个正方体棱长扩大到原来的2倍就是2,则棱长总和是2×12=24。
则这个正方体的棱长总和扩大到原来的2倍。
故选:A。
【点睛】掌握正方体的棱长总和公式是关键。
15.340
【解析】绳长为30×4+60×2+40×2+20=340(厘米)
16.355
【解析】观察图形可知,所用彩带的长度相当于两个边长是40厘米的正方形的周长和加上35厘米;据此根据正方形周长计算公式即可解题。
【详解】
40×4×2+35
=160×2+35
=320+35
=355(厘米)
所以,捆下图正方体盒子要用355厘米彩带。(打结用了35厘米彩带)
【点睛】熟记:正方形周长=边长×4,是解答此题的关键。
17.B
【解析】正方体的棱长之和=棱长×12,用60除以12,求出棱长,列式解答即可.
【详解】
60÷12=5(厘米) 答:它的棱长是5厘米.
故选B.
18.12
【解析】用150-6求出正方体的棱长总和,再根据正方体有12条棱,而且每条棱都相等可知,正方体的棱长总和除以12等于每一条棱的棱长。
【详解】
(150-6)÷12=144÷12=12(cm)
【点睛】解答本题的关键是先求出正方体的棱长总和。
19.6厘米
【解析】(8×8+2×4)÷12=72÷12=6(厘米)
或(8×4+8×4+2×4)÷12
20.A
【解析】A、折叠后有一个面重合,缺少一个底面,故不能折成正方体;
B、C、D都可以折成正方体.
故选A.
21.C
【解析】确定一个面,以一个面为底面,依次确定其它面的位置,如确定4号面为底面,找到上面即可。
【详解】
以4号面为底面,1号面为右面,2号面为前面,则3号面为上面,所以与4号面对的面是3号面。
故答案为:C
【点睛】关键是熟悉正方体特征,具有一定的空间想象能力。
22.C
【解析】根据图形判断数字1的相邻面,和数字1相邻的面一定不是数字1的相对面,最后排除数字1的相邻面即可得到数字1的相对面。
【详解】
由可知,数字2和数字3是数字1的相邻面,由可知,数字4和数字5是数字1的相邻面,数字2、3、4、5一定不是数字1的相对面,由可知,数字1的对面是数字6。
故答案为:C
【点睛】
找出数字1的相邻面用排除法得出数字1的相对面是解答题目的关键。
23.B
【解析】由题意可知,1的对面是6,2的对面是5,3的对面是4,第一次滚动后,数字4朝上,1仍朝前;第二次滚动后,1朝下,6朝上;第三次滚动后,2朝下,5朝上。
【详解】1的对面是6,2的对面是5,3的对面是4,第一次滚动后,数字4朝上;第二次滚动后,1朝下,6朝上;第三次滚动后,2朝下,5朝上。
故答案为:B
【点睛】解答此题的关键是根据题意弄清各面上的数字,然后可动手操作一下。
24.D
【解析】观察图可知,①号图形还差3个正方体就可以拼成一个正方体,⑤号图形还差2个正方体就可以拼成一个正方体,据此解答。
【详解】根据题图可知,①和④或者③和⑤可以直接拼成一个正方体。
故答案为:D。
【点睛】解答本题的关键是读懂每个立体图形的特点,进而找到与其相匹配的另一个立体图形。
25.B
【解析】根据正方体的每条棱长度都相等可知,小正方体拼一个稍大的正方体,沿长、宽、高需要各放两个小正方体,一共需要2×2×2=8个,据此解答即可。
【详解】
至少要8个棱长3厘米的小正方体可拼出一个稍大的正方体;
故答案为:B。
【点睛】
熟记正方体的特征是解答本题的关键。
26.B
【解析】根据图形可得,从下向上数,第二层缺1个;第三层缺4个;第四层缺9个;然后相加即可。
【详解】
根据分析可得
1+4+9=14(个)
故答案为:B
【点睛】本题要结合图形的正面观测到的形状,确定各层所缺的小立方体的个数是解答的突破口。
27.B
【解析】要使所用的小正方体最少,那么大正方体的棱长最少可以由2个小正方体的棱长组成,由此即可求得小正方体的个数。
【详解】2×2×2=8(个);故答案为:B。
【点睛】此题考查了小正方体拼组大正方体的特点的灵活应用。
28.C
【解析】如图,最顶层有一个小正方体,第二层有1+2=3(个)小正方体,第三层有1+2+3=6(个)小正方体,则一共有1+3+6=10(个)小正方体。
【详解】结合图示可知:1+3+6=10(个)
故答案为:C。
【点睛】本题需要我们仔细观察图示,通过分析每层的构成规律,来得到每层的小正方体个数,最后把它们相加即可。
29.D
【解析】已知这个长方体长、宽、高,即在长、宽、高这几条线段中,高7厘米是最短的。那么当我们对这个长方体进行切割时,不可能得到棱长是9厘米、或12厘米的正方体,因此,所切割得到的最大的正方体棱长为7厘米。
【详解】由分析得:
7<9<12
所以这个正方体的棱长为7厘米。
故答案为:D。
30. 24 24 8
【解析】观察图形可知,大正方体每条棱上都有4个小正方体,所以小正方体有4×4×4=64块,根据正方体表面积涂色的特点,分别得出切割后小正方体的涂色面的排列特点:
(1)没有涂色的都在内部;
(2)两面涂色的在每条棱上(除去顶点处的小正方体);
(3)一面涂色的都在每一个面上,(除去棱上的小正方体);据此即可解答。
【详解】(1)2个面涂色:(4-2)×12=2×12=24(块)
(2)1个面涂色:4×6=24(块)
(3)没有涂色:(4-2)×(4-2)×(4-2)
=2×2×2
=4×2
=8(块)
【点睛】解答本题的关键是明确;两面涂色的在每条棱长的中间上;一面涂色的在每一个面的中心上;没有涂色的在内部。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
