2021-2022学年苏科版八年级数学下册9.3平行四边形优生辅导训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学下册9.3平行四边形优生辅导训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 401.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 20:22:38 | ||
图片预览




文档简介
2021-2022学年苏科版八年级数学下册《9-3平行四边形》优生辅导训练(附答案)
一.选择题
1.如图,在 ABCD中,EF∥AD,HN∥AB,则图中的平行四边形(不包括四边形ABCD)的个数共有( )
A.9个 B.8个 C.6个 D.4个
2.下列四个说法:
①一组对角相等,一组邻角互补的四边形是平行四边形;
②一组对边平行,另一组对边相等的四边形是平行四边形;
③一组对边平行,一组对角相等的四边形是平行四边形;
④一组对边相等,一组对角相等的四边形是平行四边形;
其中说法正确的个数是( )
A.1个 B.2个 C.3个 D.4个
3.如图, ABCD中,AB=4,BC=5,AC的垂直平分线交AD于点E,则△CDE的周长是( )
A.6 B.8 C.9 D.10
4.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD=8.错误的个数是( )
A.1个 B.2个 C.3个 D.4个
5.如图,点O是 ABCD对角线的交点,EF过点O分别交AD,BC于点E,F.下列结论:①OE=OF;②AE=BF;③∠DOC=∠OCD;④∠CFE=∠DEF,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
6.如图,在平面直角坐标系xOy中,A(0,1),B(0,﹣1),C(3,0).若以A、B、C、D为顶点的四边形是平行四边形,所有符合条件的D点坐标是( )
A.(﹣3,0) B.(3,﹣2),(﹣3,0)
C.(3,2),(3,﹣2) D.(﹣3,0),(3,﹣2),(3,2)
二.填空题
7.如图,在 ABCD中,BE平分∠ABC,BC=6,DE=2,则 ABCD的周长等于 .
8.如图,在 ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB= cm.
9.如图,在 ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S AEPH= .
10.如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有 次.
11.如图,在 ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为 cm2.
12.如图,在 ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 .
二.解答题
13.如图,在平行四边形ABCD中,点E,F分别是边AD,BC的中点.
(1)求证:AF=CE;
(2)若四边形AECF的周长为10,AF=3,AB=2,求平行四边形ABCD的周长.
14.如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E、F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连接BD交AC于点O,若BD=14,AE+CF=EF,求EG的长.
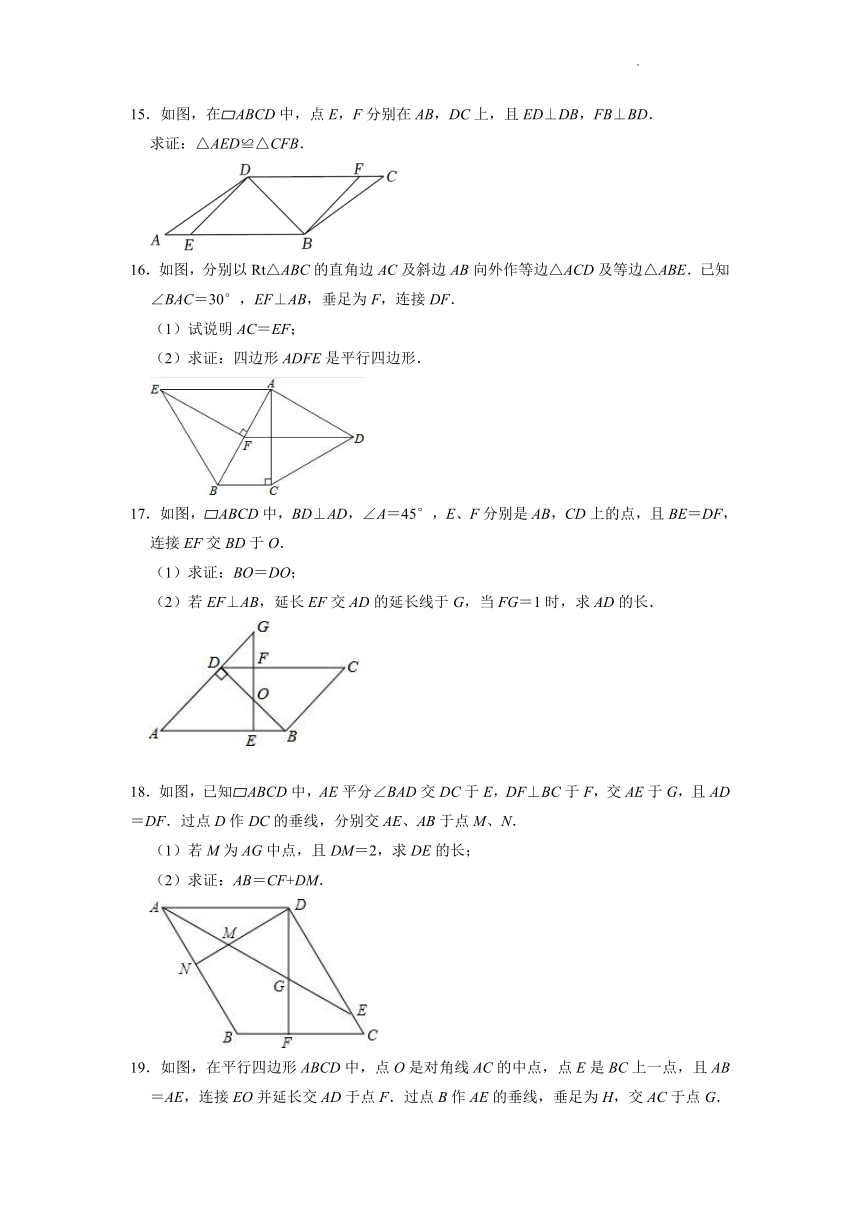
15.如图,在 ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
求证:△AED≌△CFB.
16.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
17.如图, ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
18.如图,已知 ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D作DC的垂线,分别交AE、AB于点M、N.
(1)若M为AG中点,且DM=2,求DE的长;
(2)求证:AB=CF+DM.
19.如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.
(1)若AH=3,HE=1,求△ABE的面积;
(2)若∠ACB=45°,求证:DF=CG.
20.已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
(1)证明四边形ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.
参考答案
一.选择题
1.解:设EF与NH交于点O,
∵在 ABCD中,EF∥AD,HN∥AB,
∴AD∥EF∥BC,AB∥NH∥CD,
则图中的四边BEON、DFOH、DHNC、BEFC、BAHN、AEOH、AEFD、ONCF都是平行四边形,共8个.
故选:B.
2.解:①一组对角相等,一组邻角互补.可得到任意两对邻角互补,那么可得到两组对边分别平行,为平行四边形,此选项正确;
②一组对边平行,另一组对边相等的四边形不是平行四边形,此选项错误;
③由一组对边平行,一组对角相等可得另一组对边平行,所以是平行四边形,此选项正确;
④一组对边相等,一组对角相等的四边形不能证明另一组对边也相等或平行,所以该四边形不一定是平行四边形,故本选项错误;
所以①③共2项正确,
故选:B.
3.解:∵ ABCD中,AB=4,BC=5,
∴AD=5,CD=4,
∵AC的垂直平分线交AD于点E,
∴AE=CE
∴△CDE的周长=CE+DE+CD=AE+DE+CD=AD+CD=5+4=9,
故选:C.
4.解:∵AB=3,AC=4,BC=5,32+42=52,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∴AB⊥AC,故①正确;
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=150°,
∵△ABD和△FBC都是等边三角形,
∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC,
在△ABC与△DBF中,
,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证:△ABC≌△EFC(SAS),
∴AB=EF=AD=3,
∴四边形AEFD是平行四边形,故②正确;
∴∠DFE=∠DAE=150°,故③正确;
过A作AG⊥DF于G,如图所示:
则∠AGD=90°,
∵四边形AEFD是平行四边形,
∴∠FDA=180°﹣∠DFE=180°﹣150°=30°,
∴AG=AD=,
∴S AEFD=DF AG=4×=6,故④错误;
∴错误的个数是1个,
故选:A.
5.解:∵ ABCD的对角线AC,BD交于点O,
∴AO=CO,BO=DO,AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF,AE=CF,∠CFE=∠AEF,
又∵∠DOC=∠BOA,
∴选项①成立,选项②,③,④不一定成立,
故选:A.
6.解:如图所示,符合条件的点D的坐标分别是D1(﹣3,0).
D2(3,2),D3(3,﹣2),
故选:D.
二.填空题
7.解:∵四边形ABCD为平行四边形,
∴AE∥BC,AD=BC,AB=CD,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE,
∴AE+DE=AD=BC=6,
∴AE+2=6,
∴AE=4,
∴AB=CD=4,
∴ ABCD的周长=4+4+6+6=20,
故答案为:20.
8.解:∵四边形ABCD是平行四边形,
∴BC=AD=8cm,OA=OC=AC,
∵AC⊥BC,
∴∠ACB=90°,
∴AC===6,
∴OC=3,
∴OB===;
故答案为:.
9.解:∵EF∥BC,GH∥AB,
∴四边形HPFD、BEPG、AEPH、CFPG为平行四边形,
∴S△PEB=S△BGP,
同理可得S△PHD=S△DFP,S△ABD=S△CDB,
∴S△ABD﹣S△PEB﹣S△PHD=S△CDB﹣S△BGP﹣S△DFP,
即S四边形AEPH=S四边形PFCG.
∵CG=2BG,S△BPG=1,
∴S四边形AEPH=S四边形PFCG=4×1=4;
故答案为:4.
10.解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,
∵以点P、D、Q、B为顶点组成平行四边形,
∴DP=BQ,
分为以下情况:①点Q的运动路线是C﹣B,方程为12﹣4t=12﹣t,
此时方程t=0,此时不符合题意;
②点Q的运动路线是C﹣B﹣C,方程为4t﹣12=12﹣t,
解得:t=4.8;
③点Q的运动路线是C﹣B﹣C﹣B,方程为12﹣(4t﹣24)=12﹣t,
解得:t=8;
④点Q的运动路线是C﹣B﹣C﹣B﹣C,方程为4t﹣36=12﹣t,
解得:t=9.6;
∴共3次.
故答案为:3.
11.解:连接E、F两点,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△EFC的FC边上的高与△BCF的FC边上的高相等,
∴S△EFC=S△BCF,
∴S△EFQ=S△BCQ,
同理:S△EFD=S△ADF,
∴S△EFP=S△ADP,
∵S△APD=16cm2,S△BQC=25cm2,
∴S四边形EPFQ=41cm2,
故答案为:41.
12.解:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°﹣∠EAD′﹣∠D′=108°,
∴∠FED′=108°﹣72°=36°;
故答案为:36°.
二.解答题
13.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,即AE∥CF,
又∵点E,F分别是边AD,BC的中点,
∴AE=AD,CF=BC,
∴AE=CF,
∴四边形AECF为平行四边形,
∴AF=CE;
(2)解:∵四边形AECF的周长为10,AF=3,
∴AE+CF=10﹣2×3=4,
∵点E,F分别是边AD,BC的中点,
∴AD+BC=2(AE+CF)=8,
∵AB=2,
∴平行四边形ABCD的周长=8+2×2=12.
14.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
在△AGE和△CHF中,
,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE∥HF,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)解:连接BD交AC于点O,如图:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=14,
∴OB=OD=7,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE+CF=EF,AE=CF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴EG=OB=.
15.证明:∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C,AD∥CB,AB∥CD,
∴∠ADB=∠CBD,
∵ED⊥DB,FB⊥BD,
∴∠EDB=∠FBD=90°,
∴∠ADE=∠CBF,
在△AED和△CFB中,
,
∴△AED≌△CFB(ASA).
16.证明:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF
∴AF=BC,
在Rt△AFE和Rt△BCA中,
,
∴△AFE≌△BCA(HL),
∴AC=EF;
(2)∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形.
17.(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB,
∴∠ODF=∠OBE,
在△ODF与△OBE中
∴△ODF≌△OBE(AAS)
∴BO=DO;
(2)解:∵BD⊥AD,
∴∠ADB=90°,
∵∠A=45°,
∴∠DBA=∠A=45°,
∵EF⊥AB,
∴∠G=∠A=45°,
∴△ODG是等腰直角三角形,
∵AB∥CD,EF⊥AB,
∴DF⊥OG,
∴OF=FG,△DFG是等腰直角三角形,
∵△ODF≌△OBE(AAS)
∴OE=OF,
∴GF=OF=OE,
即2FG=EF,
∵△DFG是等腰直角三角形,
∴DF=FG=1,∴DG==DO,
∴在等腰Rt△ADB 中,DB=2DO=2=AD
∴AD=2,
18.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠BAE=∠DEA,
∵AE平分∠BAD,
∴∠DAE=∠DEA,
∴DE=AD,
∵DF⊥BC,
∴DF⊥AD,
∵M为AG中点,
∴AG=2DM=4,
∵DN⊥CD,
∴∠ADM+∠MDG=∠MDG+∠EDG,
∴∠ADM=∠EDG,
∴∠DAE+∠ADM=∠DEA+∠EDG,
即∠DMG=∠DGM,
∴DG=DM=2,
在Rt△ADG中,DE=AD==;
(2)证法一:过点A作AD的垂线交DN的延长线于点H,
在△ADH和△FDC中,
,
∴△DAH≌△DFC(ASA),
∴AH=FC,DH=DC,
∵DF⊥AD,
∴AH∥DF,
∴∠HAM=∠DGM,
∵∠AMH=∠DMG,∠DMG=∠DGM,
∴∠HAM=∠HMA,
∴AH=MH,
∴MH=CF,
∴AB=CD=DH=MH+DM=CF+DM.
证法二:延长MD到点P,使DP=CF,连接PE
由(1)知AD=DE,
又AD=DF,
∴DF=DE,
∠DFC=∠EDP=90°
∴Rt△DCF≌Rt△EPD,
∴DC=EP,∠CDF=∠PED
∴PE∥DF,
∴∠PEA=∠DGA,
由(1)得∠DGA=∠DME,
∴∠PEA=∠DME
∴PM=PE,
而PM=DM+DP=DM+CF,PE=CD=AB,
∴AB=DM+FC.
证法三:过点A作AH⊥CB于点H,
易证△ABH≌△DCF,
从而证得四边形AHFD为正方形.
把△ADG绕点A顺时针旋转90°,
得△AHP,∠AHP=∠AHB=90°
∴P、H、B三点共线
∵AE平分∠BAD,
∴∠1=∠2,而∠2=∠HAP,
∴∠HAB+∠1=∠HAB+∠HAP,即∠HAG=∠PAB
∵AH∥DF,
∴∠HAG=∠DGA
而∠DGA=∠APB
∴∠PAB=∠APB
∴AB=PB
∵PB=PH+HB=DG+FC
∴AB=DM+FC.
证法四:在DC上截取DP=DM,连接PF,
∵四边形ABCD是平行四边形,
∴AB∥CD
∴∠BAE=∠DEA,
而∠BAE=∠DAE,
∴∠DAE=∠DEA DA=DE,
又∠ADF=∠MDE=90°,
∴∠ADM=∠EDG,
∴△ADM≌△EDG,
∴DM=DG,
∴DG=DP,
又AD=DF,
∴DF=DE,而∠PDF=∠FDP,
∴△PDF≌△GDE,
∴∠DPF=∠DGE,∠DFP=∠DEG,
∴∠CPF=∠DGM,
∵∠DFP+∠CFP=∠DEG+∠DMG=90°,
∴∠CFP=∠DMG,
而∠DMG=∠DGM,
∴∠CFP=∠CPF CF=CP,
而CD=DP+CP=DM+CF,AB=CD,
∴AB=DM+CF.
19.解:(1)∵AH=3,HE=1,
∴AB=AE=4,
又∵Rt△ABH中,BH==,
∴S△ABE=AE×BH=×4×=;
(2)如图,过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,则∠AMB=∠AME=∠BNG=90°,
∵∠ACB=45°,
∴∠MAC=∠NGC=45°,
∵AB=AE,
∴BM=EM=BE,∠BAM=∠EAM,
又∵AE⊥BG,
∴∠AHK=90°=∠BMK,而∠AKH=∠BKM,
∴∠MAE=∠NBG,
设∠BAM=∠MAE=∠NBG=α,则∠BAG=45°+α,∠BGA=∠GCN+∠GBC=45°+α,
∴AB=BG,
∴AE=BG,
在△AME和△BNG中,
,
∴△AME≌△BNG(AAS),
∴ME=NG,
在等腰Rt△CNG中,NG=NC,
∴GC=NG=ME=BE,
∴BE=GC,
∵O是AC的中点,
∴OA=OC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠OAF=∠OCE,∠AFO=∠CEO,
∴△AFO≌△CEO(AAS),
∴AF=CE,
∴AD﹣AF=BC﹣EC,即DF=BE,
∴DF=BE=CG.
20.(1)证明:∵BD垂直平分AC,
∴AB=BC,AD=DC,
在△ADB与△CDB中,
,
∴△ADB≌△CDB(SSS)
∴∠BCD=∠BAD,
∵∠BCD=∠ADF,
∴∠BAD=∠ADF,
∴AB∥FD,
∵BD⊥AC,AF⊥AC,
∴AF∥BD,
∴四边形ABDF是平行四边形,
(2)解:∵四边形ABDF是平行四边形,AF=DF=5,
∴ ABDF是菱形,
∴AB=BD=5,
∵AD=6,
设BE=x,则DE=5﹣x,
∴AB2﹣BE2=AD2﹣DE2,
即52﹣x2=62﹣(5﹣x)2
解得:x=,
∴=,
∴AC=2AE=.
一.选择题
1.如图,在 ABCD中,EF∥AD,HN∥AB,则图中的平行四边形(不包括四边形ABCD)的个数共有( )
A.9个 B.8个 C.6个 D.4个
2.下列四个说法:
①一组对角相等,一组邻角互补的四边形是平行四边形;
②一组对边平行,另一组对边相等的四边形是平行四边形;
③一组对边平行,一组对角相等的四边形是平行四边形;
④一组对边相等,一组对角相等的四边形是平行四边形;
其中说法正确的个数是( )
A.1个 B.2个 C.3个 D.4个
3.如图, ABCD中,AB=4,BC=5,AC的垂直平分线交AD于点E,则△CDE的周长是( )
A.6 B.8 C.9 D.10
4.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD=8.错误的个数是( )
A.1个 B.2个 C.3个 D.4个
5.如图,点O是 ABCD对角线的交点,EF过点O分别交AD,BC于点E,F.下列结论:①OE=OF;②AE=BF;③∠DOC=∠OCD;④∠CFE=∠DEF,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
6.如图,在平面直角坐标系xOy中,A(0,1),B(0,﹣1),C(3,0).若以A、B、C、D为顶点的四边形是平行四边形,所有符合条件的D点坐标是( )
A.(﹣3,0) B.(3,﹣2),(﹣3,0)
C.(3,2),(3,﹣2) D.(﹣3,0),(3,﹣2),(3,2)
二.填空题
7.如图,在 ABCD中,BE平分∠ABC,BC=6,DE=2,则 ABCD的周长等于 .
8.如图,在 ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB= cm.
9.如图,在 ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S AEPH= .
10.如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有 次.
11.如图,在 ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为 cm2.
12.如图,在 ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 .
二.解答题
13.如图,在平行四边形ABCD中,点E,F分别是边AD,BC的中点.
(1)求证:AF=CE;
(2)若四边形AECF的周长为10,AF=3,AB=2,求平行四边形ABCD的周长.
14.如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E、F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连接BD交AC于点O,若BD=14,AE+CF=EF,求EG的长.
15.如图,在 ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
求证:△AED≌△CFB.
16.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
17.如图, ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
18.如图,已知 ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D作DC的垂线,分别交AE、AB于点M、N.
(1)若M为AG中点,且DM=2,求DE的长;
(2)求证:AB=CF+DM.
19.如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.
(1)若AH=3,HE=1,求△ABE的面积;
(2)若∠ACB=45°,求证:DF=CG.
20.已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
(1)证明四边形ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.
参考答案
一.选择题
1.解:设EF与NH交于点O,
∵在 ABCD中,EF∥AD,HN∥AB,
∴AD∥EF∥BC,AB∥NH∥CD,
则图中的四边BEON、DFOH、DHNC、BEFC、BAHN、AEOH、AEFD、ONCF都是平行四边形,共8个.
故选:B.
2.解:①一组对角相等,一组邻角互补.可得到任意两对邻角互补,那么可得到两组对边分别平行,为平行四边形,此选项正确;
②一组对边平行,另一组对边相等的四边形不是平行四边形,此选项错误;
③由一组对边平行,一组对角相等可得另一组对边平行,所以是平行四边形,此选项正确;
④一组对边相等,一组对角相等的四边形不能证明另一组对边也相等或平行,所以该四边形不一定是平行四边形,故本选项错误;
所以①③共2项正确,
故选:B.
3.解:∵ ABCD中,AB=4,BC=5,
∴AD=5,CD=4,
∵AC的垂直平分线交AD于点E,
∴AE=CE
∴△CDE的周长=CE+DE+CD=AE+DE+CD=AD+CD=5+4=9,
故选:C.
4.解:∵AB=3,AC=4,BC=5,32+42=52,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∴AB⊥AC,故①正确;
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=150°,
∵△ABD和△FBC都是等边三角形,
∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC,
在△ABC与△DBF中,
,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证:△ABC≌△EFC(SAS),
∴AB=EF=AD=3,
∴四边形AEFD是平行四边形,故②正确;
∴∠DFE=∠DAE=150°,故③正确;
过A作AG⊥DF于G,如图所示:
则∠AGD=90°,
∵四边形AEFD是平行四边形,
∴∠FDA=180°﹣∠DFE=180°﹣150°=30°,
∴AG=AD=,
∴S AEFD=DF AG=4×=6,故④错误;
∴错误的个数是1个,
故选:A.
5.解:∵ ABCD的对角线AC,BD交于点O,
∴AO=CO,BO=DO,AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF,AE=CF,∠CFE=∠AEF,
又∵∠DOC=∠BOA,
∴选项①成立,选项②,③,④不一定成立,
故选:A.
6.解:如图所示,符合条件的点D的坐标分别是D1(﹣3,0).
D2(3,2),D3(3,﹣2),
故选:D.
二.填空题
7.解:∵四边形ABCD为平行四边形,
∴AE∥BC,AD=BC,AB=CD,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE,
∴AE+DE=AD=BC=6,
∴AE+2=6,
∴AE=4,
∴AB=CD=4,
∴ ABCD的周长=4+4+6+6=20,
故答案为:20.
8.解:∵四边形ABCD是平行四边形,
∴BC=AD=8cm,OA=OC=AC,
∵AC⊥BC,
∴∠ACB=90°,
∴AC===6,
∴OC=3,
∴OB===;
故答案为:.
9.解:∵EF∥BC,GH∥AB,
∴四边形HPFD、BEPG、AEPH、CFPG为平行四边形,
∴S△PEB=S△BGP,
同理可得S△PHD=S△DFP,S△ABD=S△CDB,
∴S△ABD﹣S△PEB﹣S△PHD=S△CDB﹣S△BGP﹣S△DFP,
即S四边形AEPH=S四边形PFCG.
∵CG=2BG,S△BPG=1,
∴S四边形AEPH=S四边形PFCG=4×1=4;
故答案为:4.
10.解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,
∵以点P、D、Q、B为顶点组成平行四边形,
∴DP=BQ,
分为以下情况:①点Q的运动路线是C﹣B,方程为12﹣4t=12﹣t,
此时方程t=0,此时不符合题意;
②点Q的运动路线是C﹣B﹣C,方程为4t﹣12=12﹣t,
解得:t=4.8;
③点Q的运动路线是C﹣B﹣C﹣B,方程为12﹣(4t﹣24)=12﹣t,
解得:t=8;
④点Q的运动路线是C﹣B﹣C﹣B﹣C,方程为4t﹣36=12﹣t,
解得:t=9.6;
∴共3次.
故答案为:3.
11.解:连接E、F两点,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△EFC的FC边上的高与△BCF的FC边上的高相等,
∴S△EFC=S△BCF,
∴S△EFQ=S△BCQ,
同理:S△EFD=S△ADF,
∴S△EFP=S△ADP,
∵S△APD=16cm2,S△BQC=25cm2,
∴S四边形EPFQ=41cm2,
故答案为:41.
12.解:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°﹣∠EAD′﹣∠D′=108°,
∴∠FED′=108°﹣72°=36°;
故答案为:36°.
二.解答题
13.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,即AE∥CF,
又∵点E,F分别是边AD,BC的中点,
∴AE=AD,CF=BC,
∴AE=CF,
∴四边形AECF为平行四边形,
∴AF=CE;
(2)解:∵四边形AECF的周长为10,AF=3,
∴AE+CF=10﹣2×3=4,
∵点E,F分别是边AD,BC的中点,
∴AD+BC=2(AE+CF)=8,
∵AB=2,
∴平行四边形ABCD的周长=8+2×2=12.
14.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
在△AGE和△CHF中,
,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE∥HF,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)解:连接BD交AC于点O,如图:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=14,
∴OB=OD=7,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE+CF=EF,AE=CF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴EG=OB=.
15.证明:∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C,AD∥CB,AB∥CD,
∴∠ADB=∠CBD,
∵ED⊥DB,FB⊥BD,
∴∠EDB=∠FBD=90°,
∴∠ADE=∠CBF,
在△AED和△CFB中,
,
∴△AED≌△CFB(ASA).
16.证明:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF
∴AF=BC,
在Rt△AFE和Rt△BCA中,
,
∴△AFE≌△BCA(HL),
∴AC=EF;
(2)∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形.
17.(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB,
∴∠ODF=∠OBE,
在△ODF与△OBE中
∴△ODF≌△OBE(AAS)
∴BO=DO;
(2)解:∵BD⊥AD,
∴∠ADB=90°,
∵∠A=45°,
∴∠DBA=∠A=45°,
∵EF⊥AB,
∴∠G=∠A=45°,
∴△ODG是等腰直角三角形,
∵AB∥CD,EF⊥AB,
∴DF⊥OG,
∴OF=FG,△DFG是等腰直角三角形,
∵△ODF≌△OBE(AAS)
∴OE=OF,
∴GF=OF=OE,
即2FG=EF,
∵△DFG是等腰直角三角形,
∴DF=FG=1,∴DG==DO,
∴在等腰Rt△ADB 中,DB=2DO=2=AD
∴AD=2,
18.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠BAE=∠DEA,
∵AE平分∠BAD,
∴∠DAE=∠DEA,
∴DE=AD,
∵DF⊥BC,
∴DF⊥AD,
∵M为AG中点,
∴AG=2DM=4,
∵DN⊥CD,
∴∠ADM+∠MDG=∠MDG+∠EDG,
∴∠ADM=∠EDG,
∴∠DAE+∠ADM=∠DEA+∠EDG,
即∠DMG=∠DGM,
∴DG=DM=2,
在Rt△ADG中,DE=AD==;
(2)证法一:过点A作AD的垂线交DN的延长线于点H,
在△ADH和△FDC中,
,
∴△DAH≌△DFC(ASA),
∴AH=FC,DH=DC,
∵DF⊥AD,
∴AH∥DF,
∴∠HAM=∠DGM,
∵∠AMH=∠DMG,∠DMG=∠DGM,
∴∠HAM=∠HMA,
∴AH=MH,
∴MH=CF,
∴AB=CD=DH=MH+DM=CF+DM.
证法二:延长MD到点P,使DP=CF,连接PE
由(1)知AD=DE,
又AD=DF,
∴DF=DE,
∠DFC=∠EDP=90°
∴Rt△DCF≌Rt△EPD,
∴DC=EP,∠CDF=∠PED
∴PE∥DF,
∴∠PEA=∠DGA,
由(1)得∠DGA=∠DME,
∴∠PEA=∠DME
∴PM=PE,
而PM=DM+DP=DM+CF,PE=CD=AB,
∴AB=DM+FC.
证法三:过点A作AH⊥CB于点H,
易证△ABH≌△DCF,
从而证得四边形AHFD为正方形.
把△ADG绕点A顺时针旋转90°,
得△AHP,∠AHP=∠AHB=90°
∴P、H、B三点共线
∵AE平分∠BAD,
∴∠1=∠2,而∠2=∠HAP,
∴∠HAB+∠1=∠HAB+∠HAP,即∠HAG=∠PAB
∵AH∥DF,
∴∠HAG=∠DGA
而∠DGA=∠APB
∴∠PAB=∠APB
∴AB=PB
∵PB=PH+HB=DG+FC
∴AB=DM+FC.
证法四:在DC上截取DP=DM,连接PF,
∵四边形ABCD是平行四边形,
∴AB∥CD
∴∠BAE=∠DEA,
而∠BAE=∠DAE,
∴∠DAE=∠DEA DA=DE,
又∠ADF=∠MDE=90°,
∴∠ADM=∠EDG,
∴△ADM≌△EDG,
∴DM=DG,
∴DG=DP,
又AD=DF,
∴DF=DE,而∠PDF=∠FDP,
∴△PDF≌△GDE,
∴∠DPF=∠DGE,∠DFP=∠DEG,
∴∠CPF=∠DGM,
∵∠DFP+∠CFP=∠DEG+∠DMG=90°,
∴∠CFP=∠DMG,
而∠DMG=∠DGM,
∴∠CFP=∠CPF CF=CP,
而CD=DP+CP=DM+CF,AB=CD,
∴AB=DM+CF.
19.解:(1)∵AH=3,HE=1,
∴AB=AE=4,
又∵Rt△ABH中,BH==,
∴S△ABE=AE×BH=×4×=;
(2)如图,过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,则∠AMB=∠AME=∠BNG=90°,
∵∠ACB=45°,
∴∠MAC=∠NGC=45°,
∵AB=AE,
∴BM=EM=BE,∠BAM=∠EAM,
又∵AE⊥BG,
∴∠AHK=90°=∠BMK,而∠AKH=∠BKM,
∴∠MAE=∠NBG,
设∠BAM=∠MAE=∠NBG=α,则∠BAG=45°+α,∠BGA=∠GCN+∠GBC=45°+α,
∴AB=BG,
∴AE=BG,
在△AME和△BNG中,
,
∴△AME≌△BNG(AAS),
∴ME=NG,
在等腰Rt△CNG中,NG=NC,
∴GC=NG=ME=BE,
∴BE=GC,
∵O是AC的中点,
∴OA=OC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠OAF=∠OCE,∠AFO=∠CEO,
∴△AFO≌△CEO(AAS),
∴AF=CE,
∴AD﹣AF=BC﹣EC,即DF=BE,
∴DF=BE=CG.
20.(1)证明:∵BD垂直平分AC,
∴AB=BC,AD=DC,
在△ADB与△CDB中,
,
∴△ADB≌△CDB(SSS)
∴∠BCD=∠BAD,
∵∠BCD=∠ADF,
∴∠BAD=∠ADF,
∴AB∥FD,
∵BD⊥AC,AF⊥AC,
∴AF∥BD,
∴四边形ABDF是平行四边形,
(2)解:∵四边形ABDF是平行四边形,AF=DF=5,
∴ ABDF是菱形,
∴AB=BD=5,
∵AD=6,
设BE=x,则DE=5﹣x,
∴AB2﹣BE2=AD2﹣DE2,
即52﹣x2=62﹣(5﹣x)2
解得:x=,
∴=,
∴AC=2AE=.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
