27.3.2 平面直角坐标系中的位似 课件(共14张PPT)
文档属性
| 名称 | 27.3.2 平面直角坐标系中的位似 课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 286.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 18:54:29 | ||
图片预览



文档简介
(共14张PPT)
人教版 九年级数学下册
第27章 相似
27.3 位似
第2课时 平面直角坐标系中的位似
B'
A'
x
y
B
A
O
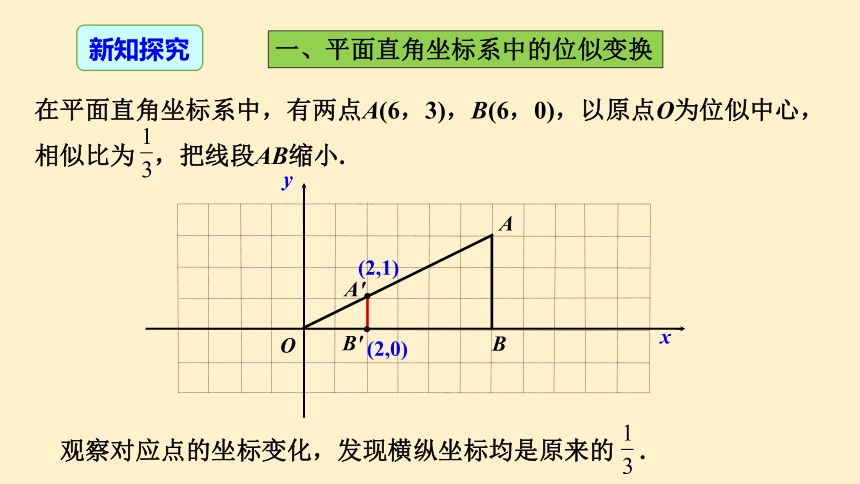
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为 ,把线段AB缩小.
(2,1)
观察对应点的坐标变化,发现横纵坐标均是原来的 .
(2,0)
一、平面直角坐标系中的位似变换
新知探究
B'
A'
x
y
B
A
O
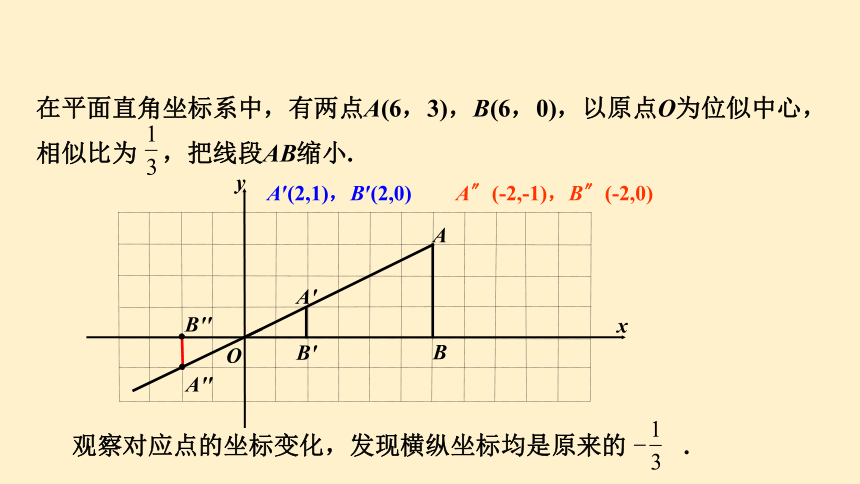
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为 ,把线段AB缩小.
A′(2,1),B′(2,0)
A''
B''
A〞(-2,-1),B〞(-2,0)
观察对应点的坐标变化,发现横纵坐标均是原来的 .
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
O
9
10
11
12
-9
-10
-12
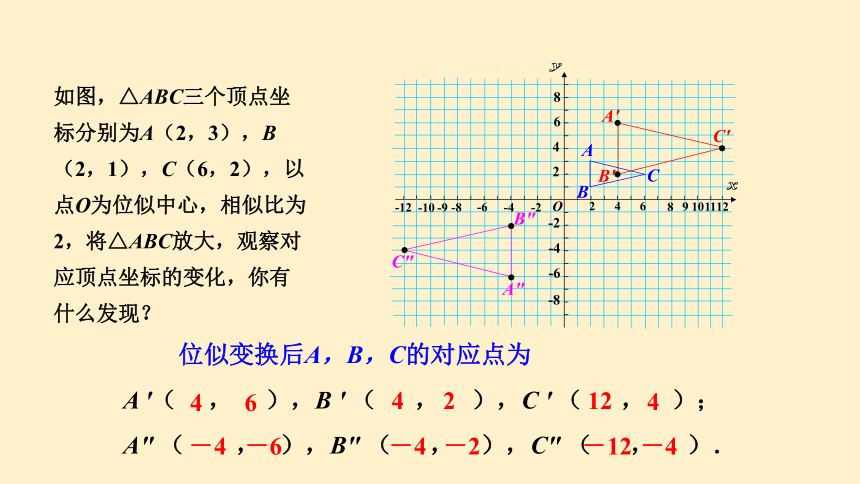
如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?
A
B
C
位似变换后A,B,C的对应点为
A '( , ),B ' ( , ),C ' ( , );
A" ( , ),B" ( , ),C" ( , ).
4
6
4
2
12
4
-4
-6
-4
-2
-4
-12
A'
B'
C'
A"
B"
C"
小组讨论:
在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
2. 在平面直角坐标系中,以原点为位似中心,相似比为k,对应点的坐标变化有什么规律?
反思
1. 如图,线段 AB 两个端点的坐标分别为 A (4,4),B (6,2),以原点 O 为位似中心,在第一象限内将线段 AB 缩小为原来的 后得到线段 CD,则端点 D 的坐标为 ( )
A. (2,2) B. (2,1)
C. (3,2) D. (3,1)
D
x
y
A
B
C
D
O
针对训练
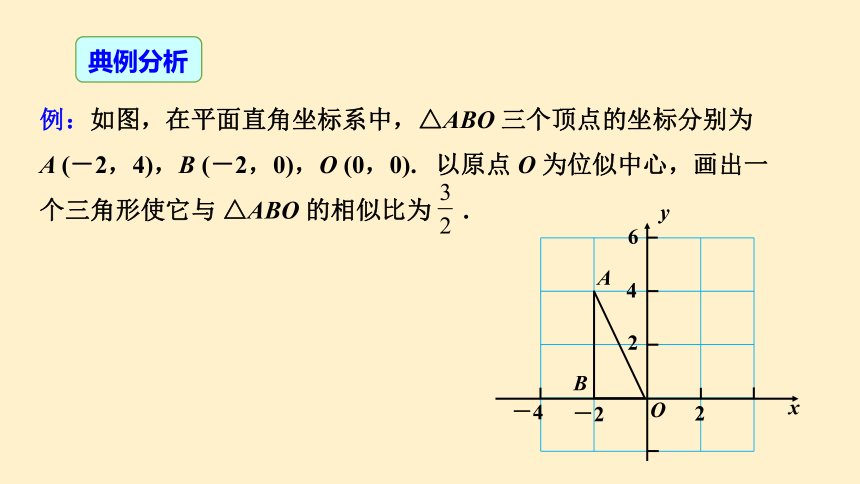
例:如图,在平面直角坐标系中,△ABO 三个顶点的坐标分别为 A (-2,4),B (-2,0),O (0,0). 以原点 O 为位似中心,画出一个三角形使它与 △ABO 的相似比为 .
2
4
6
2
-2
-4
x
y
A
B
O
典例分析
2
4
6
2
-2
-4
x
y
A
B
O
解:利用位似中对应点的坐标的变化规律,先分别找到:
A ( -2,4 ) ,B ( -2,0),O ( 0,0),
横纵坐标均乘以 , 得到对应点坐标: A′ (-3,6),B′ (-3,0),O (0,0).
A′
B′
顺次连接点 A′ ,B′ ,O,所得的 △A′ B′ O 就是要画的一个图形.
还有其他画法吗?
1. 将平面直角坐标系中某个图形的各点坐标做如下变化,其中属于位似变换的是 ( )
A. 将各点的纵坐标乘以 2,横坐标不变
B. 将各点的横坐标除以 2,纵坐标不变
C. 将各点的横坐标、纵坐标都乘以 2
D. 将各点的纵坐标减去 2,横坐标加上 2
C
当堂巩固
2. 已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标分别变成原来的2倍,得到点A′,B′,C′.下列说法正确的是( )
A.△A′B′C′与△ABC是位似图形,位似中心是点(1,0)
B.△A′B′C′与△ABC是位似图形,位似中心是点(0,0)
C.△A′B′C′与△ABC是相似图形,但不是位似图形
D.△A′B′C′与△ABC不是相似图形
B
3. 如图,某学习小组在讨论 “变化的鱼”时,知道大鱼与小鱼是位似图形,则小鱼上的点 (a,b) 对应大鱼上的点 .
(-2a,-2b)
1.(4分)(2021 重庆B卷4/26)如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的相似比是( )
A.2:1 B.1:2 C.3:1 D.1:3
【解答】解:∵B(0,1),D(0,3).
∴OB=1,OD=3.
∵△OAB以原点O为位似中心放大后得到△OCD.
∴△OAB与△OCD的相似比是OB:OD=1:3.
故选:D.
感受中考
平面直角坐标系中的位似
平面直角坐标系中的位似变换
平面直角坐标系中的图形变换
坐标变化规律
平面直角坐标系中的位似图形的画法
在平面直角坐标系中,以原点O为位似中心,位似比为k,若原图形上点p的坐标为(x,y),那么位似图形对应点p'的坐标为(kx,ky)或(-kx,-ky)
先根据变化规律计算出对应点的坐标,然后描点并顺次连接.
平移,轴对称,旋转(中心对称),位似
课堂小结
P51:习题27.3:第3、5题.
P52:习题27.3:第6、7题.
布置作业
人教版 九年级数学下册
第27章 相似
27.3 位似
第2课时 平面直角坐标系中的位似
B'
A'
x
y
B
A
O
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为 ,把线段AB缩小.
(2,1)
观察对应点的坐标变化,发现横纵坐标均是原来的 .
(2,0)
一、平面直角坐标系中的位似变换
新知探究
B'
A'
x
y
B
A
O
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为 ,把线段AB缩小.
A′(2,1),B′(2,0)
A''
B''
A〞(-2,-1),B〞(-2,0)
观察对应点的坐标变化,发现横纵坐标均是原来的 .
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
O
9
10
11
12
-9
-10
-12
如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?
A
B
C
位似变换后A,B,C的对应点为
A '( , ),B ' ( , ),C ' ( , );
A" ( , ),B" ( , ),C" ( , ).
4
6
4
2
12
4
-4
-6
-4
-2
-4
-12
A'
B'
C'
A"
B"
C"
小组讨论:
在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
2. 在平面直角坐标系中,以原点为位似中心,相似比为k,对应点的坐标变化有什么规律?
反思
1. 如图,线段 AB 两个端点的坐标分别为 A (4,4),B (6,2),以原点 O 为位似中心,在第一象限内将线段 AB 缩小为原来的 后得到线段 CD,则端点 D 的坐标为 ( )
A. (2,2) B. (2,1)
C. (3,2) D. (3,1)
D
x
y
A
B
C
D
O
针对训练
例:如图,在平面直角坐标系中,△ABO 三个顶点的坐标分别为 A (-2,4),B (-2,0),O (0,0). 以原点 O 为位似中心,画出一个三角形使它与 △ABO 的相似比为 .
2
4
6
2
-2
-4
x
y
A
B
O
典例分析
2
4
6
2
-2
-4
x
y
A
B
O
解:利用位似中对应点的坐标的变化规律,先分别找到:
A ( -2,4 ) ,B ( -2,0),O ( 0,0),
横纵坐标均乘以 , 得到对应点坐标: A′ (-3,6),B′ (-3,0),O (0,0).
A′
B′
顺次连接点 A′ ,B′ ,O,所得的 △A′ B′ O 就是要画的一个图形.
还有其他画法吗?
1. 将平面直角坐标系中某个图形的各点坐标做如下变化,其中属于位似变换的是 ( )
A. 将各点的纵坐标乘以 2,横坐标不变
B. 将各点的横坐标除以 2,纵坐标不变
C. 将各点的横坐标、纵坐标都乘以 2
D. 将各点的纵坐标减去 2,横坐标加上 2
C
当堂巩固
2. 已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标分别变成原来的2倍,得到点A′,B′,C′.下列说法正确的是( )
A.△A′B′C′与△ABC是位似图形,位似中心是点(1,0)
B.△A′B′C′与△ABC是位似图形,位似中心是点(0,0)
C.△A′B′C′与△ABC是相似图形,但不是位似图形
D.△A′B′C′与△ABC不是相似图形
B
3. 如图,某学习小组在讨论 “变化的鱼”时,知道大鱼与小鱼是位似图形,则小鱼上的点 (a,b) 对应大鱼上的点 .
(-2a,-2b)
1.(4分)(2021 重庆B卷4/26)如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的相似比是( )
A.2:1 B.1:2 C.3:1 D.1:3
【解答】解:∵B(0,1),D(0,3).
∴OB=1,OD=3.
∵△OAB以原点O为位似中心放大后得到△OCD.
∴△OAB与△OCD的相似比是OB:OD=1:3.
故选:D.
感受中考
平面直角坐标系中的位似
平面直角坐标系中的位似变换
平面直角坐标系中的图形变换
坐标变化规律
平面直角坐标系中的位似图形的画法
在平面直角坐标系中,以原点O为位似中心,位似比为k,若原图形上点p的坐标为(x,y),那么位似图形对应点p'的坐标为(kx,ky)或(-kx,-ky)
先根据变化规律计算出对应点的坐标,然后描点并顺次连接.
平移,轴对称,旋转(中心对称),位似
课堂小结
P51:习题27.3:第3、5题.
P52:习题27.3:第6、7题.
布置作业
