2021-2022学年北师大版八年级数学下册第一章三角形的证明单元测试训练卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册第一章三角形的证明单元测试训练卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 283.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 00:00:00 | ||
图片预览



文档简介
北师大版八年级数学下册
第一章 三角形的证明
单元测试训练卷
一、选择题(共10小题,每小题4分,共40分)
1. 如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,若∠1=20°,则∠2的度数为( )
A.25° B.65° C.70° D.75°
2. 已知点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上任意一点,则下列结论正确的是( )
A.PQ≤5 B.PQ<5 C.PQ≥5 D.PQ>5
3. 如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )
A.6 B.6 C.9 D.3
4. 如图,地面上有三个洞口A,B,C,老鼠可以从任意一个洞口跑出去,猫为能最省力地顾及到三个洞口(到A,B,C三个点的距离相等),尽快抓到老鼠,应该蹲守在( )
A.△ABC三边垂直平分线的交点处
B.△ABC三条角平分线的交点处
C.△ABC三条高所在直线的交点处
D.△ABC三条中线的交点处
5. 通过如下尺规作图,能确定点D是BC边中点的是( )
6. 如图所示,在△ABC与△ABD中,∠C=∠D=90°,要使△ABC≌△ABD(HL)成立,还需要添加的条件是( )
A.∠BAC=∠BAD B.BC=BD或AC=AD
C.∠ABC=∠ABD D.AB为公共边
7. 如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD B.CD垂直平分AB
C.AB与CD互相垂直平分 D.CD平分∠ACB
8. 过直线l外一点P作l的垂线,先在直线l上取两点A,B,使PA=PB,再作( )
A.线段AB的垂线 B.∠PAB的平分线
C.∠PBA的平分线 D.∠APB的平分线
9. 如图,在Rt△ABE中,∠B=90°,延长BE到C,使EC=AB,分别过点C,E作BC,AE的垂线,两线相交于点D,连接AD.若AB=3,DC=4,则AD的长是( )
A.5 B.7 C.5 D.无法确定
10. 如图,在△ABC中,∠BAC=90°,∠ABC=30°,以AB,AC为边向外分别作等边三角形ABD和等边三角形ACE.若AC=2,则BE的长为( )
A.6 B.2 C. D.5
二.填空题(共6小题,每小题4分,共24分)
11. “垂直于同一条直线的两条直线互相平行”的逆命题是__ __(填“真”或“假”)命题.
12. 如图,一个等边三角形的纸片剪去一个角后得到一个四边形,则图中∠α+∠β的度数是_________.
13. 如图,DA⊥AC,DE⊥BC,垂足分别为A,E,若DA=5 cm,DE=5 cm,∠ACD=30°,则∠DCE的度数为__ __.
14. 如图,△ABC的周长为22 cm,AB的垂直平分线交AC于点E,垂足为D,若△BCE的周长为14 cm,则AB=__ __cm.
15. 如图,一架2.6 m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4 m,当梯子的顶端A沿墙向下滑的距离AC与梯子底端B向外移的距离BD相等时,AC的长是____.
16. 如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的是_____________.(填序号)
三.解答题(共6小题, 56分)
17.(6分) 如图,在△ABC中,点P是AC上一点,连接BP,求作一点M,使得点M到AB和AC两边的距离相等,并且到点B和点P的距离相等.(不写作法,保留作图痕迹)
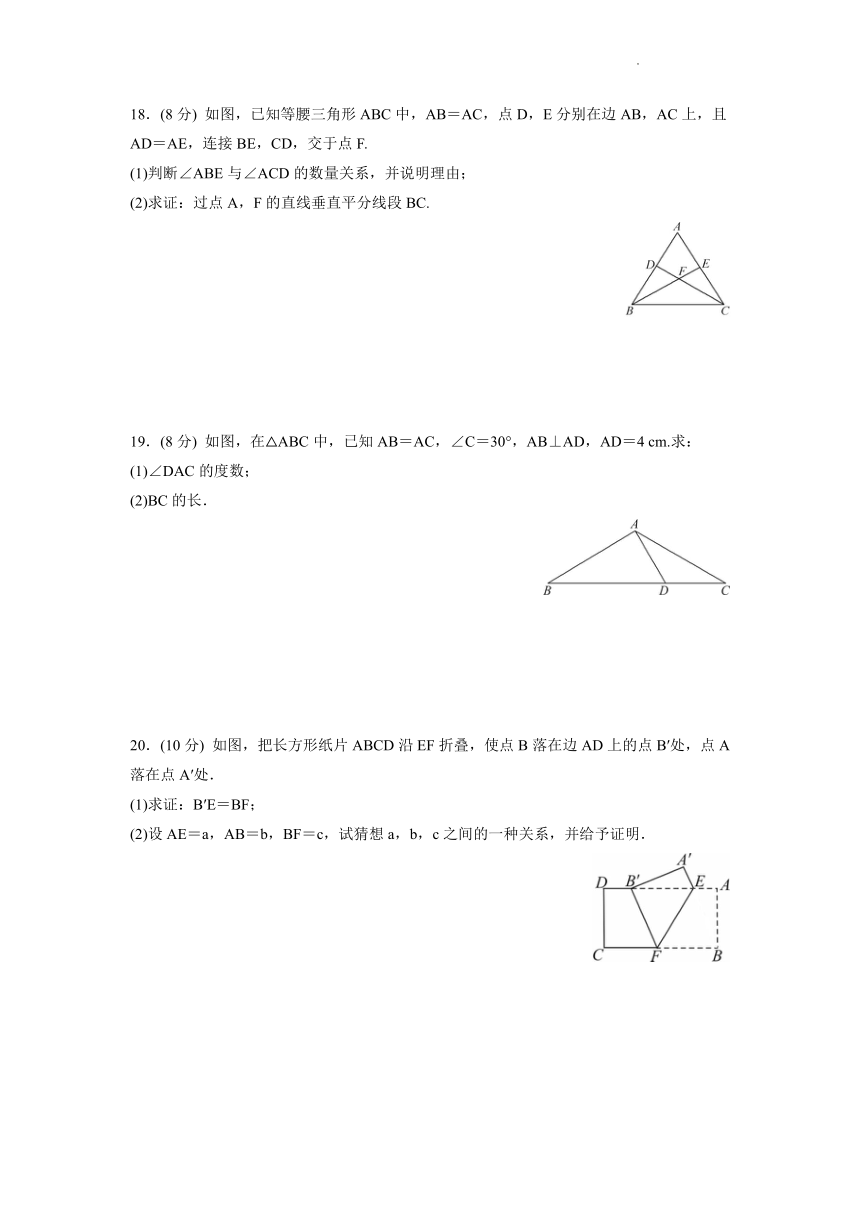
18.(8分) 如图,已知等腰三角形ABC中,AB=AC,点D,E分别在边AB,AC上,且AD=AE,连接BE,CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A,F的直线垂直平分线段BC.
19.(8分) 如图,在△ABC中,已知AB=AC,∠C=30°,AB⊥AD,AD=4 cm.求:
(1)∠DAC的度数;
(2)BC的长.
20.(10分) 如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处.
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的一种关系,并给予证明.
21.(12分) 已知:如图,锐角三角形ABC的两条高BD,CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
22.(12分) 如图,在△ABC中,AB=BC=AC=12 cm,现有两点M,N分别从点A,点B同时出发,沿三角形的边运动,已知点M的速度为1 cm/s,点N的速度为2 cm/s.当点N第一次回到B点时,点M,N同时停止运动.
(1)点M,N运动几秒后,M,N两点重合?
(2)点M,N运动几秒后,可得到等边三角形AMN
(3)当点M,N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?若存在,请求出此时M,N运动的时间.
参考答案
1-5BCCAA 6-10AAACDBACCB
11.真
12.240°
13.30°
14.8
15.1.4m
16.①②③④
17.解:点M即为所求
18.解:(1)∠ABE=∠ACD.理由如下:在△ABE和△ACD中,∴△ABE≌△ACD,∴∠ABE=∠ACD.(2)证明:∵AB=AC,∴∠ABC=∠ACB,由(1)可知∠ABE=∠ACD,∴∠FBC=∠FCB,∴FB=FC, ∵AB=AC,∴点A,F均在线段BC的垂直平分线上,即直线AF垂直平分线段BC.
19.解:(1)∵AB=AC,∠C=30°,∴∠B=30°,∴∠BAC=180°-30°-30°=120°.∵AB⊥AD,∴∠DAC=120°-90°=30°
(2)∵AD=4 cm,∠B=30°,∠BAD=90°,∴BD=8 cm.∵∠DAC=30°=∠C,∴DC=AD=4 cm,∴BC=BD+DC=12 cm
20.解:(1)证明:由题意得B′F=BF,∠B′FE=∠BFE.又∵AD∥BC,∴∠B′EF=∠BFE,∴∠B′FE=∠B′EF,∴B′F=B′E,∴B′E=BF (2)a,b,c的关系为a2+b2=c2,连接BE,则BE=B′E,由(1)知B′E=BF=c,∴BE=c.∵AE2+AB2=BE2,又∵AE=a,AB=b,∴a2+b2=c2(若写a+b>c也可以)
21.(1)证明:∵OB=OC,∴∠OBC=∠OCB.∵锐角三角形ABC的两条高BD,CE相交于点O,∴∠BEC=∠BDC=90°.∴∠BCE+∠ABC=∠DBC+∠ACB=90°.∴∠ABC=∠ACB.∴AB=AC,即△ABC是等腰三角形.
(2)解:点O在∠BAC的平分线上.理由:在△EOB和△DOC中, ∴△EOB≌△DOC(AAS).∴OE=OD.又∵OE⊥AE,OD⊥AD,∴点O在∠BAC的平分线上.
22.解:(1)设点M,N运动x秒后,M,N两点重合,则x+12=2x,解得x=12,故点M,N运动12秒后,M,N两点重合.
(2)设点M,N运动t秒后,可得到等边三角形AMN,如图①,AM=t,AN=AB-BN=12-2t,∵三角形AMN是等边三角形,∴t=12-2t,解得t=4,∴点M,N运动4秒后,可得到等边三角形AMN.
(3)当点M,N在BC边上运动时,可以得到以MN为底边的等腰三角形AMN,由(1)知12秒时M,N两点重合,恰好在C处,如图②,假设△AMN是以边MN为底边的等腰三角形,∴AN=AM,∴∠AMN=∠ANM,∴∠AMC=∠ANB,∵AB=BC=AC,∴△ACB是等边三角形,∴∠C=∠B,∴△ACM≌△ABN,∴CM=BN,设当点M,N在BC边上运动时,M,N运动的时间为y秒时,△AMN是以边MN为底边的等腰三角形,∴CM=y-12,NB=36-2y,又∵CM=NB,∴y-12=36-2y,解得y=16.∴当点M,N在BC边上运动时,能得到以MN为底边的等腰三角形AMN,此时M,N运动的时间为16秒.
第一章 三角形的证明
单元测试训练卷
一、选择题(共10小题,每小题4分,共40分)
1. 如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,若∠1=20°,则∠2的度数为( )
A.25° B.65° C.70° D.75°
2. 已知点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上任意一点,则下列结论正确的是( )
A.PQ≤5 B.PQ<5 C.PQ≥5 D.PQ>5
3. 如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )
A.6 B.6 C.9 D.3
4. 如图,地面上有三个洞口A,B,C,老鼠可以从任意一个洞口跑出去,猫为能最省力地顾及到三个洞口(到A,B,C三个点的距离相等),尽快抓到老鼠,应该蹲守在( )
A.△ABC三边垂直平分线的交点处
B.△ABC三条角平分线的交点处
C.△ABC三条高所在直线的交点处
D.△ABC三条中线的交点处
5. 通过如下尺规作图,能确定点D是BC边中点的是( )
6. 如图所示,在△ABC与△ABD中,∠C=∠D=90°,要使△ABC≌△ABD(HL)成立,还需要添加的条件是( )
A.∠BAC=∠BAD B.BC=BD或AC=AD
C.∠ABC=∠ABD D.AB为公共边
7. 如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD B.CD垂直平分AB
C.AB与CD互相垂直平分 D.CD平分∠ACB
8. 过直线l外一点P作l的垂线,先在直线l上取两点A,B,使PA=PB,再作( )
A.线段AB的垂线 B.∠PAB的平分线
C.∠PBA的平分线 D.∠APB的平分线
9. 如图,在Rt△ABE中,∠B=90°,延长BE到C,使EC=AB,分别过点C,E作BC,AE的垂线,两线相交于点D,连接AD.若AB=3,DC=4,则AD的长是( )
A.5 B.7 C.5 D.无法确定
10. 如图,在△ABC中,∠BAC=90°,∠ABC=30°,以AB,AC为边向外分别作等边三角形ABD和等边三角形ACE.若AC=2,则BE的长为( )
A.6 B.2 C. D.5
二.填空题(共6小题,每小题4分,共24分)
11. “垂直于同一条直线的两条直线互相平行”的逆命题是__ __(填“真”或“假”)命题.
12. 如图,一个等边三角形的纸片剪去一个角后得到一个四边形,则图中∠α+∠β的度数是_________.
13. 如图,DA⊥AC,DE⊥BC,垂足分别为A,E,若DA=5 cm,DE=5 cm,∠ACD=30°,则∠DCE的度数为__ __.
14. 如图,△ABC的周长为22 cm,AB的垂直平分线交AC于点E,垂足为D,若△BCE的周长为14 cm,则AB=__ __cm.
15. 如图,一架2.6 m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4 m,当梯子的顶端A沿墙向下滑的距离AC与梯子底端B向外移的距离BD相等时,AC的长是____.
16. 如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的是_____________.(填序号)
三.解答题(共6小题, 56分)
17.(6分) 如图,在△ABC中,点P是AC上一点,连接BP,求作一点M,使得点M到AB和AC两边的距离相等,并且到点B和点P的距离相等.(不写作法,保留作图痕迹)
18.(8分) 如图,已知等腰三角形ABC中,AB=AC,点D,E分别在边AB,AC上,且AD=AE,连接BE,CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A,F的直线垂直平分线段BC.
19.(8分) 如图,在△ABC中,已知AB=AC,∠C=30°,AB⊥AD,AD=4 cm.求:
(1)∠DAC的度数;
(2)BC的长.
20.(10分) 如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处.
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的一种关系,并给予证明.
21.(12分) 已知:如图,锐角三角形ABC的两条高BD,CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
22.(12分) 如图,在△ABC中,AB=BC=AC=12 cm,现有两点M,N分别从点A,点B同时出发,沿三角形的边运动,已知点M的速度为1 cm/s,点N的速度为2 cm/s.当点N第一次回到B点时,点M,N同时停止运动.
(1)点M,N运动几秒后,M,N两点重合?
(2)点M,N运动几秒后,可得到等边三角形AMN
(3)当点M,N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?若存在,请求出此时M,N运动的时间.
参考答案
1-5BCCAA 6-10AAACDBACCB
11.真
12.240°
13.30°
14.8
15.1.4m
16.①②③④
17.解:点M即为所求
18.解:(1)∠ABE=∠ACD.理由如下:在△ABE和△ACD中,∴△ABE≌△ACD,∴∠ABE=∠ACD.(2)证明:∵AB=AC,∴∠ABC=∠ACB,由(1)可知∠ABE=∠ACD,∴∠FBC=∠FCB,∴FB=FC, ∵AB=AC,∴点A,F均在线段BC的垂直平分线上,即直线AF垂直平分线段BC.
19.解:(1)∵AB=AC,∠C=30°,∴∠B=30°,∴∠BAC=180°-30°-30°=120°.∵AB⊥AD,∴∠DAC=120°-90°=30°
(2)∵AD=4 cm,∠B=30°,∠BAD=90°,∴BD=8 cm.∵∠DAC=30°=∠C,∴DC=AD=4 cm,∴BC=BD+DC=12 cm
20.解:(1)证明:由题意得B′F=BF,∠B′FE=∠BFE.又∵AD∥BC,∴∠B′EF=∠BFE,∴∠B′FE=∠B′EF,∴B′F=B′E,∴B′E=BF (2)a,b,c的关系为a2+b2=c2,连接BE,则BE=B′E,由(1)知B′E=BF=c,∴BE=c.∵AE2+AB2=BE2,又∵AE=a,AB=b,∴a2+b2=c2(若写a+b>c也可以)
21.(1)证明:∵OB=OC,∴∠OBC=∠OCB.∵锐角三角形ABC的两条高BD,CE相交于点O,∴∠BEC=∠BDC=90°.∴∠BCE+∠ABC=∠DBC+∠ACB=90°.∴∠ABC=∠ACB.∴AB=AC,即△ABC是等腰三角形.
(2)解:点O在∠BAC的平分线上.理由:在△EOB和△DOC中, ∴△EOB≌△DOC(AAS).∴OE=OD.又∵OE⊥AE,OD⊥AD,∴点O在∠BAC的平分线上.
22.解:(1)设点M,N运动x秒后,M,N两点重合,则x+12=2x,解得x=12,故点M,N运动12秒后,M,N两点重合.
(2)设点M,N运动t秒后,可得到等边三角形AMN,如图①,AM=t,AN=AB-BN=12-2t,∵三角形AMN是等边三角形,∴t=12-2t,解得t=4,∴点M,N运动4秒后,可得到等边三角形AMN.
(3)当点M,N在BC边上运动时,可以得到以MN为底边的等腰三角形AMN,由(1)知12秒时M,N两点重合,恰好在C处,如图②,假设△AMN是以边MN为底边的等腰三角形,∴AN=AM,∴∠AMN=∠ANM,∴∠AMC=∠ANB,∵AB=BC=AC,∴△ACB是等边三角形,∴∠C=∠B,∴△ACM≌△ABN,∴CM=BN,设当点M,N在BC边上运动时,M,N运动的时间为y秒时,△AMN是以边MN为底边的等腰三角形,∴CM=y-12,NB=36-2y,又∵CM=NB,∴y-12=36-2y,解得y=16.∴当点M,N在BC边上运动时,能得到以MN为底边的等腰三角形AMN,此时M,N运动的时间为16秒.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
