27.2.2 相似三角形应用举例
文档属性
| 名称 | 27.2.2 相似三角形应用举例 |  | |
| 格式 | zip | ||
| 文件大小 | 800.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-26 19:55:58 | ||
图片预览





文档简介
课件17张PPT。 在古希腊,有一位伟大的数学家、天文学家叫泰勒斯,一天,希腊国王阿马西斯对他说:“听说你什么都知道,那就请你测量一下埃及金字塔的高度吧!”这在当时条件下是个大难题,因为是很难爬到塔顶的。
一连几天,他站在金字塔下,用不同的工具都无法测出它的高度,他又失望、又伤心地坐在金字塔下,难过极了,忽然他注意到广场的地面上有许多人影,灵机一动,他决定利用影长来测定金字塔的高度。你知道泰勒斯是如何利用影长测量金字塔的高度的吗?相关情资泰勒斯:古希腊第一位科学家 利用三角形的相似,可以解决一些不能直接测量的物体的高度、宽度等问题。27.2.2相似三角形应用举例学习目标1.进一步巩固相似三角形的知识.
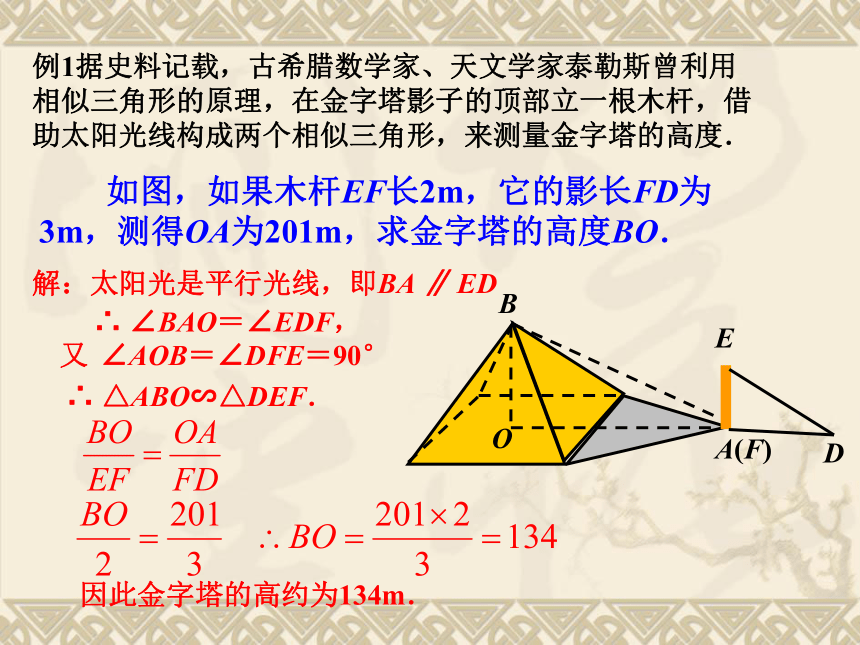
2.能够运用三角形相似的知识,解决不能直接测量物体的长度和高度(如测量金字塔高度问题、测量河宽问题、盲区问题)等的一些实际问题. 例1据史料记载,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度. 如图,如果木杆EF长2m,它的影长FD为3m,测得OA为201m,求金字塔的高度BO.解:太阳光是平行光线,即BA ∥ ED∠AOB=∠DFE=90°∴ △ABO∽△DEF.因此金字塔的高约为134m.又∴ ∠BAO=∠EDF, 解法二:用镜面反射:
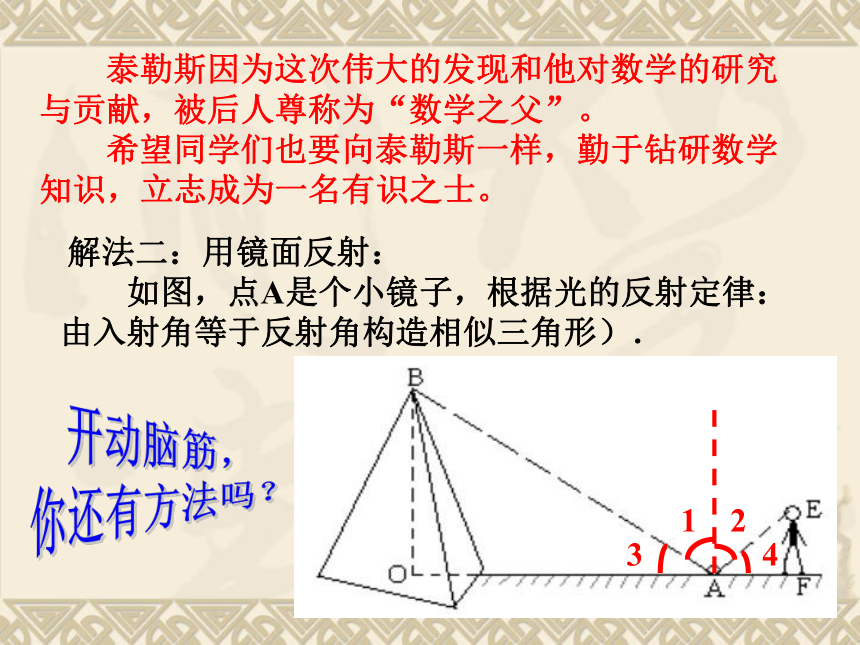
如图,点A是个小镜子,根据光的反射定律:
由入射角等于反射角构造相似三角形). 泰勒斯因为这次伟大的发现和他对数学的研究
与贡献,被后人尊称为“数学之父”。
希望同学们也要向泰勒斯一样,勤于钻研数学
知识,立志成为一名有识之士。1234开动脑筋,
你还有方法吗?例2 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.解:∵ ∠PQR=∠PST=90°,∠P=∠P,x×90=(x+45)×60解得 x=90.∴ △PQR∽△PST.因此河宽PQ大约为90m设PQ=x你能想出其它方法测量河的宽度吗? 开动脑筋解法二:如图构造相似三角形 例3 已知左、右并排的两棵大树的高分别是AB=8cm和CD=12m,两树的根部的距离BD=5m.一个身高1.6m的人沿着正对这两棵树的一条水平直路 l 从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C?分析:如图,说观察者眼睛的位置为点F,画出观察者的水平视线FG,它交AB、CD于点H、K.视线FA、FG的夹角∠CFK是观察点C时的仰角.由于树的遮挡,区域1 和11都在观察者看不到的区域(盲区)之内.HK仰角视线水平线AC解:如图,假设观察者从左向右走到点E时,他的眼睛的位置点F与两棵树顶端点A、C恰在一条直线上.由题意可知,AB⊥l,CD⊥l∴ AB∥CD,△AFH∽△CFK即解得 FH=8由此可知,如果观察者继续前进,即他与左边的树的距离小于8m时,由于这棵树的遮挡,右边树的顶端点C在观察者的盲区之内,观察者看不到它.1、在某一时刻,测得一根高为1.8m的竹竿的影长为 3m,同时测得一栋高楼的影长为90m,这栋高楼的高度是多少?易得△ABC ∽ △A'B'C'求得 A'C'=54m答:这栋高楼的高度是54m.解:牛刀小试由题意画图, 2、王东同学为了测量我们美丽的洹河宽度,他
想出了一个这样的办法,以对面岸边的电线杆
为标志点O,在自己的岸边选点A、B、D,使AB⊥AO,DB⊥AB,然后确定DO和AB的交点C。
然后测得AC=27米,CB=3米,BD=10米,你能帮
助他算出洹河的宽度吗?牛刀小试安
阳
洹
河3、如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高 m。 1m16m0.5m8给我一个支点我可以撬起整个地球!---阿基米德?牛刀小试4、小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.(设网球是直线运动)
ADBCE┏┏0.8m5m10m?牛刀小试一 、相似三角形的应用主要有如下两个方面
1 测高(不易直接使用皮尺或刻度尺量的)
2 测距(不易直接测量的两点间的距离)、测高的方法
测量不易到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决。 、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解。解决实际问题时(如测高、测距),一般有以下步骤:
①审题
②构建图形
③利用相似解决问题
归纳小结,强化思想
一连几天,他站在金字塔下,用不同的工具都无法测出它的高度,他又失望、又伤心地坐在金字塔下,难过极了,忽然他注意到广场的地面上有许多人影,灵机一动,他决定利用影长来测定金字塔的高度。你知道泰勒斯是如何利用影长测量金字塔的高度的吗?相关情资泰勒斯:古希腊第一位科学家 利用三角形的相似,可以解决一些不能直接测量的物体的高度、宽度等问题。27.2.2相似三角形应用举例学习目标1.进一步巩固相似三角形的知识.
2.能够运用三角形相似的知识,解决不能直接测量物体的长度和高度(如测量金字塔高度问题、测量河宽问题、盲区问题)等的一些实际问题. 例1据史料记载,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度. 如图,如果木杆EF长2m,它的影长FD为3m,测得OA为201m,求金字塔的高度BO.解:太阳光是平行光线,即BA ∥ ED∠AOB=∠DFE=90°∴ △ABO∽△DEF.因此金字塔的高约为134m.又∴ ∠BAO=∠EDF, 解法二:用镜面反射:
如图,点A是个小镜子,根据光的反射定律:
由入射角等于反射角构造相似三角形). 泰勒斯因为这次伟大的发现和他对数学的研究
与贡献,被后人尊称为“数学之父”。
希望同学们也要向泰勒斯一样,勤于钻研数学
知识,立志成为一名有识之士。1234开动脑筋,
你还有方法吗?例2 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.解:∵ ∠PQR=∠PST=90°,∠P=∠P,x×90=(x+45)×60解得 x=90.∴ △PQR∽△PST.因此河宽PQ大约为90m设PQ=x你能想出其它方法测量河的宽度吗? 开动脑筋解法二:如图构造相似三角形 例3 已知左、右并排的两棵大树的高分别是AB=8cm和CD=12m,两树的根部的距离BD=5m.一个身高1.6m的人沿着正对这两棵树的一条水平直路 l 从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C?分析:如图,说观察者眼睛的位置为点F,画出观察者的水平视线FG,它交AB、CD于点H、K.视线FA、FG的夹角∠CFK是观察点C时的仰角.由于树的遮挡,区域1 和11都在观察者看不到的区域(盲区)之内.HK仰角视线水平线AC解:如图,假设观察者从左向右走到点E时,他的眼睛的位置点F与两棵树顶端点A、C恰在一条直线上.由题意可知,AB⊥l,CD⊥l∴ AB∥CD,△AFH∽△CFK即解得 FH=8由此可知,如果观察者继续前进,即他与左边的树的距离小于8m时,由于这棵树的遮挡,右边树的顶端点C在观察者的盲区之内,观察者看不到它.1、在某一时刻,测得一根高为1.8m的竹竿的影长为 3m,同时测得一栋高楼的影长为90m,这栋高楼的高度是多少?易得△ABC ∽ △A'B'C'求得 A'C'=54m答:这栋高楼的高度是54m.解:牛刀小试由题意画图, 2、王东同学为了测量我们美丽的洹河宽度,他
想出了一个这样的办法,以对面岸边的电线杆
为标志点O,在自己的岸边选点A、B、D,使AB⊥AO,DB⊥AB,然后确定DO和AB的交点C。
然后测得AC=27米,CB=3米,BD=10米,你能帮
助他算出洹河的宽度吗?牛刀小试安
阳
洹
河3、如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高 m。 1m16m0.5m8给我一个支点我可以撬起整个地球!---阿基米德?牛刀小试4、小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.(设网球是直线运动)
ADBCE┏┏0.8m5m10m?牛刀小试一 、相似三角形的应用主要有如下两个方面
1 测高(不易直接使用皮尺或刻度尺量的)
2 测距(不易直接测量的两点间的距离)、测高的方法
测量不易到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决。 、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解。解决实际问题时(如测高、测距),一般有以下步骤:
①审题
②构建图形
③利用相似解决问题
归纳小结,强化思想
