北师大版八下数学第一章三角形的证明 压轴题选编(word版、含解析)
文档属性
| 名称 | 北师大版八下数学第一章三角形的证明 压轴题选编(word版、含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 685.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 00:00:00 | ||
图片预览



文档简介
三角形的证明压轴题选编
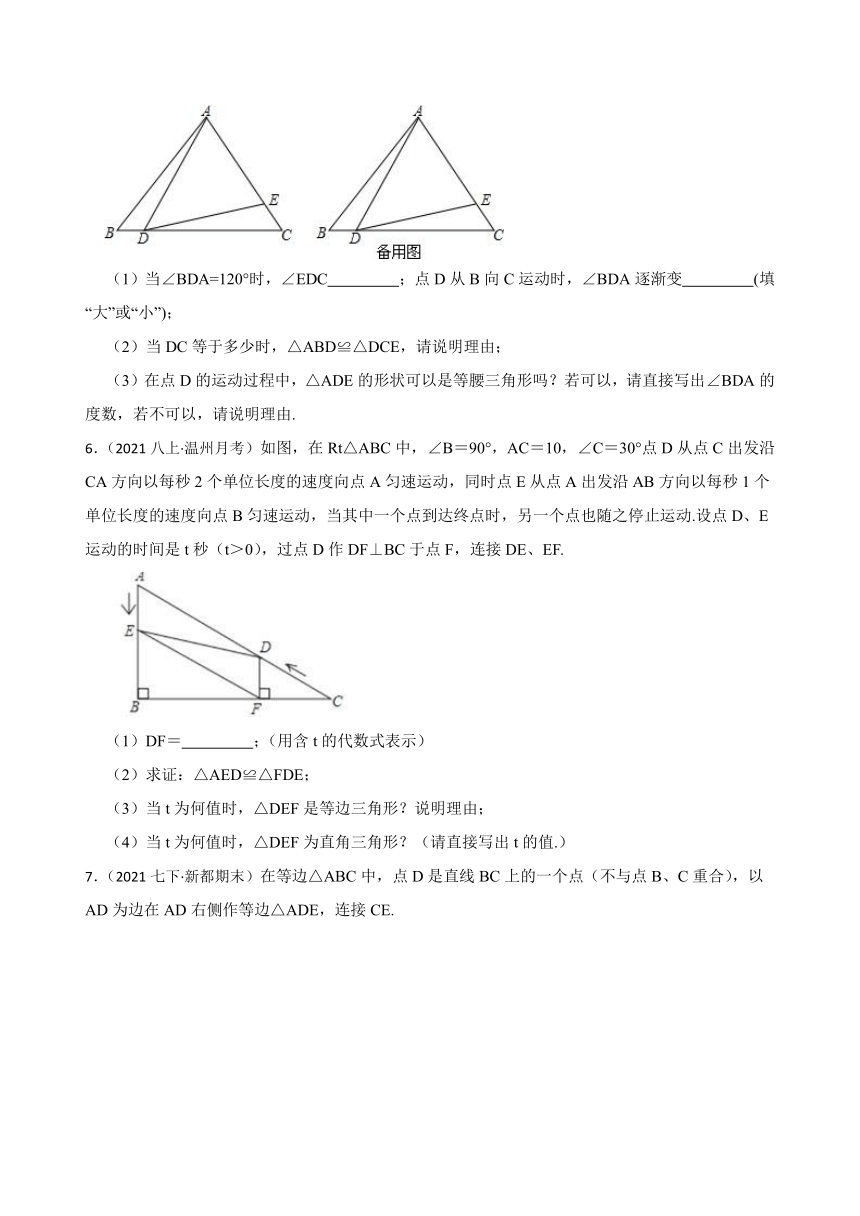
1.(2019八上·越秀期中)已知:在等腰三角形ABC中,AB=AC,AD⊥BC于点D,以AC为边作等边三角形ACE,直线BE交直线AD于点F,连接FC.
(1)如图1,120°<∠BAC<180°,△ACE与△ABC在直线AC的异侧,且FC交AE于点M.
①求证:∠FEA=∠FCA;
②猜想线段FE,AD,FD之间的数量关系,并证明你的结论;
(2)当60°<∠BAC<120°,且△ACE与△ABC在直线AC的异侧时,利用图2画出图形探究线段FE,AD,FD之间的数量关系,并直接写出你的结论.
2.(2019八上·南开期中)如图,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.
(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.
3.问题情境:如图①,在△ABD与△CAE中,BD=AE,∠DBA=∠EAC,AB=AC,易证:△ABD≌△CAE.(不需要证明)
特例探究:如图②,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F.求证:△ABD≌△CAE.
归纳证明:如图③,在等边△ABC中,点D、E分别在边CB、BA的延长线上,且BD=AE.△ABD与△CAE是否全等?如果全等,请证明;如果不全等,请说明理由.
拓展应用:如图④,在等腰三角形中,AB=AC,点O是AB边的垂直平分线与AC的交点,点D、E分别在OB、BA的延长线上.若BD=AE,∠BAC=50°,∠AEC=32°,求∠BAD的度数.
4.如图,已知在△ABC中,AB=AC=10cm,BC=8cm,D为AB中点,设点P在线段BC上以3cm/秒的速度由B点向C点运动,点Q在线段CA上由C点向A点运动.
(1)若Q点运动的速度与P点相同,且点P,Q同时出发,经过1秒钟后△BPD与△CQP是否全等,并说明理由;
(2)若点P,Q同时出发,但运动的速度不相同,当Q点的运动速度为多少时,能在运动过程中有△BPD与△CQP全等?
(3)若点Q以(2)中的速度从点C出发,点P以原来的速度从点B同时出发,都是逆时针沿△ABC的三边上运动,经过多少时间点P与点Q第一次在△ABC的哪条边上相遇?
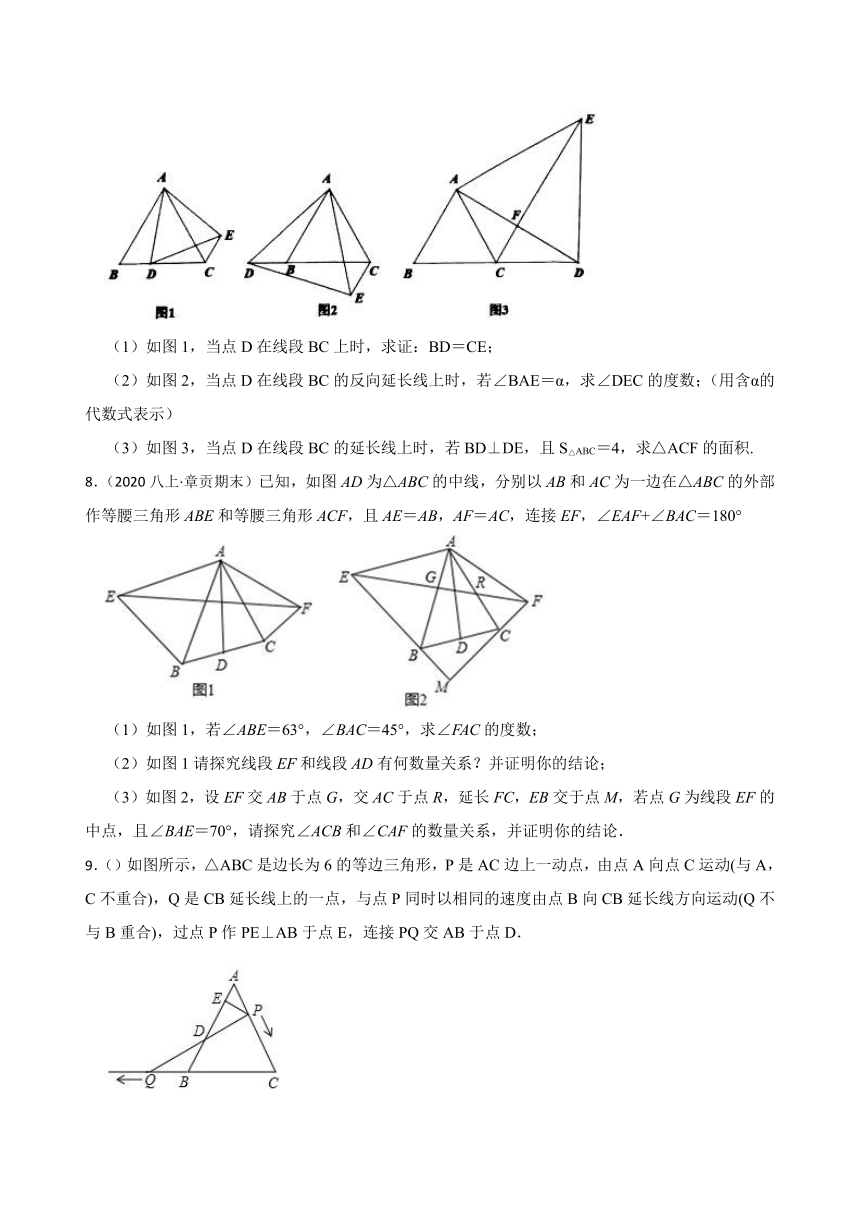
5.(2021八上·灌云月考)如图,在△ABC中,AB=AC=4,∠B=∠C=50°,点D在线段BC上运动(D不与B,C重合),连接AD,作∠ADE=50°,DE交线段AC于E.
(1)当∠BDA=120°时,∠EDC ;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数,若不可以,请说明理由.
6.(2021八上·温州月考)如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)DF= ;(用含t的代数式表示)
(2)求证:△AED≌△FDE;
(3)当t为何值时,△DEF是等边三角形?说明理由;
(4)当t为何值时,△DEF为直角三角形?(请直接写出t的值.)
7.(2021七下·新都期末)在等边△ABC中,点D是直线BC上的一个点(不与点B、C重合),以AD为边在AD右侧作等边△ADE,连接CE.
(1)如图1,当点D在线段BC上时,求证:BD=CE;
(2)如图2,当点D在线段BC的反向延长线上时,若∠BAE=α,求∠DEC的度数;(用含α的代数式表示)
(3)如图3,当点D在线段BC的延长线上时,若BD⊥DE,且S△ABC=4,求△ACF的面积.
8.(2020八上·章贡期末)已知,如图AD为△ABC的中线,分别以AB和AC为一边在△ABC的外部作等腰三角形ABE和等腰三角形ACF,且AE=AB,AF=AC,连接EF,∠EAF+∠BAC=180°
(1)如图1,若∠ABE=63°,∠BAC=45°,求∠FAC的度数;
(2)如图1请探究线段EF和线段AD有何数量关系?并证明你的结论;
(3)如图2,设EF交AB于点G,交AC于点R,延长FC,EB交于点M,若点G为线段EF的中点,且∠BAE=70°,请探究∠ACB和∠CAF的数量关系,并证明你的结论.
9.()如图所示,△ABC是边长为6的等边三角形,P是AC边上一动点,由点A向点C运动(与A,C不重合),Q是CB延长线上的一点,与点P同时以相同的速度由点B向CB延长线方向运动(Q不与B重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.
(1)当∠BQD=30°时,求AP的长.
(2)试说明:在运动过程中,点D是线段PQ的中点.
(3)在运动过程中,线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化,请说明理由.
10.(2020八上·农安期末)完成下面问题:
(1)问题发现:如图, 和 均为等边三角形,点 , , 在同一直线上,连接 ,填空:① 的度数为 ;②线段 , 之间的数量关系为 ;
(2)拓展探究:如图, 和 均为等腰直角三角形, ,点 , , 在同一直线上, 为 中 边上的高,连接 ,请判断 的度数及线段 , , 之间的数量关系,并说明理由.
11.(2021·孝感模拟)在 中, , 于点 , 为 上一点(不与 , 重合),
(1)如图1,若 ,求证: 平分 ;
(2)如图2,若 ,过点 作 于点 ,交 于 .
①求证: ;
②当 时, 与 的数量关系是▲.
12.(2020八上·沭阳期中)如图①, 和 是等腰三角形,且 , , , ,以 为顶点作一个 角,角的两边分别交边 , 于点 、 ,连接 .
(1)探究 、 、 之间的关系,并说明理由;
(2)若点 、 分别在 、CA延长线上,其他条件不变,如图②所示,则 、 、 之间存在什么样的关系?并说明理由.
13.(2021八上·包河期末)在等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE交DE于点F,连接FC.
(1)如图1,求证:∠ABE=∠ACF;
(2)如图2,当∠ABC=60°时,在BE上取点M,使BM=EF,连接AM.求证:△AFM是等边三角形;
(3)如图3,当∠ABC=45°,且AEBC时,求证:BD=2EF.
14.(2021八上·盐湖期中)定义:顶角相等且顶点重合的两个等腰三角形叫做对顶三角形.如图1,在 OAB与 OCD中,OA=OB,OC=OD,∠AOB=∠COD.
(1)如图1, OAB与 OCD是对顶三角形,且A,O,C三点共线请判断AB与CD的位置关系,并说明理由.
(2)如图2, OAB与 OCD是对顶三角形,∠AOB=∠COD=90°,连接AC,BD,试探究线段AC,BD之间的关系,并说明理由.
(3)如图3, OAB与 OCD是对顶三角形,∠AOB=∠COD=90°,连接AD,BC,取AD的中点E,连接EO并延长交BC于点F,延长OE至点G,使EG=OE,连接AG,求证:EF⊥BC.
15.(2021八上·莒南期中)如图,点 是等边 内的一点, .以 为边作等边 ,使 和 在直线 的同侧,连接 .
(1) 与 全等吗 说明你的理由;
(2)当 时,试判断 的形状,并说明理由;
(3)当 为多少度时, 是等腰三角形 请直接写出答案.
16.(2021八上·江汉期中)如图,在 中, 是角平分线, 于点 , 在边AC上, .
(1)如图1,若 ,求证: ;
(2)如图2,求证: ;
(3)若 , , ,直接写出 的长.
17.(2021·太原模拟)综合与实践
问题背景:数学小组在一次课外学习交流时,组内一同学提出如下问题:在 中, ,D为 边上一点,但不与点B,点C重合,过点D作 于点E.连接 ,M为 的中点,连接 , .
(1)观察发现:如图1, 与 之间的数量关系是 ;
(2)思考分享:如图2,将 绕点B顺时针旋转,其他条件不变,则(1)中的结论还成立,请证明.小明是这样思考的:延长 至点 ,使得 ,连接 运用三角形中位线定理,….按照他的思路或采用其他方法证明;
(3)探究计算:若 , , ,在 绕点B旋转一周的过程中,当直线 经过点A时,线段 的长为 .
18.(2020八上·滨海期末)在 中, , , 平分 交 于点E, 交 延长线于点D,连接 ,过点C作 交 于F.
(1)如图①,①求 的度数;
②求证: ;
(2)如图②, 交 的延长线于点M,探究 之间的数量关系,并给出证明.
19.(2020八上·重庆月考)已知,在等边△ABC 中,D、E 分别为 AC、BC 边上的点,BE=CD,连接 AE、BD 相交于点 F.
(1)如图 1,求∠AFD的度数;
(2)如图 2,过点A作AH⊥BD于H,若EF=HD,求证:BF=HF;
(3)如图 3,在(2)的条件下,延长BD到点M,连接AM,使∠AMB=∠ABM,若EF=2, AF=10,求DM长.
20.(2020八下·成都期中)已知Rt△ABC中,∠BAC=90°,AB=AC,点E为△ABC内一点,连接AE,CE,CE⊥AE,过点B作BD⊥AE,交AE的延长线于D.
(1)如图1,求证BD=AE;
(2)如图2,点H为BC中点,分别连接EH,DH,求∠EDH的度数;
(3)如图3,在(2)的条件下,点M为CH上的一点,连接EM,点F为EM的中点,连接FH,过点D作DG⊥FH,交FH的延长线于点G,若GH:FH=6:5,△FHM的面积为30,∠EHB=∠BHG,求线段EH的长.
21.(2019八上·南平期中)在 中, ,点 为射线 上一个动点(不与 重合),以 为一边在 的右侧作 ,使 , ,过点 作 ,交直线 于点 ,连接 .
(1)如图①,若 ,则按边分类: 是 三角形,并证明;
(2)若 .
①如图②,当点 在线段 上移动时,判断 的形状并证明;
②当点 在线段 的延长线上移动时, 是什么三角形?请在图③中画出相应的图形并直接写出结论(不必证明).
22.(2019八上·江山期中)如图1,△ABC中,CD⊥AB于D,且BD=4,AD=6,CD=8.
(1)求证:∠ACB=∠ABC;
(2)如图2,E为AC的中点,连结DE.动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时另一个点也停止运动.设点M运动的时间为t(秒),
①若MN与BC平行,求t的值;
②问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.
23.(2019七下·西安期末)如图
(1)如图1,在△ABC中,∠ACB是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F,
①请你猜想写出FE与FD之间的数量关系,不用说明理由;
②判断∠AFC与∠B的数量关系,请说明理由.
(2)如图2,在△ABC中,如果∠ACB不是直角,而(1)中其他条件不变,请问你在(1)中所得FE与FD之间的数量关系是否依然成立?请说明理由.
24.如图,已知∠AOB=120°,在∠AOB的平分线OM上有一点C,将一个60°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;
(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?若成立,请给于证明;若不成立,线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
25.如图,在平面直角坐标系中,A(﹣3,0),点B是y轴正半轴上一动点,点C、D在x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长 .
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接QD并延长,交y轴于点P,当点C运动到什么位置时,满足PD= DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在y轴上运动时,求OP的最小值.
26.(1)【问题探究】如图①已知锐角△ABC,分别以AB、AC为腰,在△ABC的外部作等腰Rt△ABD和Rt△ACE,连接CD、BE,是猜想CD、BE的大小关系 ;(不必证明)
(2)【深入探究】如图②△ABC、△ADE都是等腰直角三角形,点D在边BC上(不与B、C重合),连接EC,则线段BC,DC,EC之间满足的等量关系式为 ;(不必证明)线段AD2,BD2,CD2之间满足的等量关系,并证明你的结论;
(3)【拓展应用】如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.
答案与解析
1.【答案】(1)证明:①∵△AEC是等边三角形
∴∠EAC=∠ACE=60°,CE=AC=AE,且AB=AC
∴AB=AE
∴∠ABF=∠AEF
∵AB=AC,AD⊥BC
∴AD是BC的垂直平分线
∴BF=FC,且AF=AF,AB=AC
∴△ABF≌△ACF(SSS)
∴∠ABF=∠ACF
∴∠ACF=∠AEF
②EF=FD+AD
延长AD使DP=AD,连接CP
∵AD=DP,∠ADC=∠PDC,CD=CD
∴△ADC≌△PDC(SAS)
∴AC=CP=CE,∠ACD=∠PCD
∵∠ACF=∠AEF,且∠AMC=∠FME
∴∠EFC=∠EAC=60°
∵BF=CF,且∠EFC=60°
∴∠FCD=30°
∵∠FCA=∠FCD-∠ACD
∴∠FCA=30°-∠ACD
∵∠ECF=∠ECA-∠FCA
∴∠ECF=30°+∠ACD
∵∠FCP=∠FCD+∠DCP
∴∠FCP=30°+∠ACD
∴∠ECF=∠FCP,且FC=FC,CP=CE
∴△ECF≌△FCP(SAS)
∴EF=FP
∴EF=FD+AD
(2)解:连接CF,延长AD使FD=DP,连接CP.
∵△AEC是等边三角形
∴∠EAC=∠ACE=60°,CE=AC=AE,且AB=AC
∴AB=AE
∴∠ABF=∠AEF
∵AB=AC,AD⊥BC
∴AD是BC的垂直平分线
∴BF=FC,且AF=AF,AB=AC
∴△ABF≌△ACF(SSS)
∴∠ABF=∠ACF
∴∠ACF=∠AEF且∠AME=∠CMF
∴∠EAC=∠EFC=60°
∵BF=CF,∠EFC=60°
∴∠FCB=30°
∵FD=DP,∠FDC=∠PDC,CD=CD
∴△FDC≌△PDC(SAS)
∴FC=CP,∠FCD=∠PCD=30°
∴∠FCP=60°=∠ACE
∴∠ACP=∠FCE且CF=CP,AC=CE
∴△ACP≌△ECF(SAS)
∴EF=AP
∴EF=AD+DP=AD+DF.
2.【答案】(1)解:∵在Rt△ABO中,∠BAO=30°,
∴AB=2BO=2.
(2)证明:连接OD,
∵△ABE为等边三角形,
∴AB=AE,∠EAB=60°,
∵∠BAO=30°,作OA的垂直平分线MN交AB的垂线AD于点D,
∴∠DAO=60°.
∴∠EAO=∠NAB
又∵DO=DA,
∴△ADO为等边三角形.
∴DA=AO.
在△ABD与△AEO中,
∵ ,
∴△ABD≌△AEO(SAS).
∴BD=OE.
(3)证明:作EH⊥AB于H.
∵AE=BE,∴AH= AB,
∵BO= AB,∴AH=BO,
在Rt△AEH与Rt△BAO中,
,
∴Rt△AEH≌Rt△BAO(HL),
∴EH=AO=AD.
又∵∠EHF=∠DAF=90°,
在△HFE与△AFD中,
,
∴△HFE≌△AFD(AAS),
∴EF=DF.
∴F为DE的中点.
3.【答案】特例探究:证明:∵△ABC是等边三角形,∴AB=AC,∠DBA=∠EAC=60°,在△ABD与△CAE中, ,∴△ABD≌△CAE(SAS);归纳证明:证明:△ABD与△CAE全等.理由如下:∵△ABC是等边三角形,∴AB=AC,∠ABC=∠BAC=60°,∴∠DBA=∠EAC=120°.在△ABD与△CAE中, ,∴△ABD≌△CAE(SAS);拓展应用:解:∵点O在AB的垂直平分线上,∴OA=OB,∴∠OBA=∠BAC=50°,∴∠EAC=∠DBA.在△ABD与△CAE中, ,∴△ABD≌△CAE(SAS),∴∠BDA=∠AEC=32°,∴∠BAD=∠OBA﹣∠BDA=18°.
4.【答案】(1)解:∵t=1秒,
∴BP=CQ=3×1=3cm,
∵AB=10cm,点D为AB的中点,
∴BD=5cm.
又∵PC=BC﹣BP,BC=8cm,
∴PC=8﹣3=5cm,
∴PC=BD.
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,
∴△BPD≌△CQP(SAS).
(2)解:∵vP≠vQ,∴BP≠CQ,
又∵△BPD≌△CPQ,∠B=∠C,则BP=PC=4cm,CQ=BD=5cm,
∴点P,点Q运动的时间 秒,
∴vQ= cm/秒;
(3)设经过x秒后点P与点Q第一次相遇,
由题意,得 x=3x+2×10,
解得x= .
∴点P共运动了 ×3=80cm.
∴80=56+24=2×28+24,
∴点P、点Q在AB边上相遇,
∴经过 秒点P与点Q第一次在边AB上相遇.
5.【答案】(1)10;小
(2)解:当DC=4时,△ABD≌△DCE,
理由:∵∠C=50°,
∴∠DEC+∠EDC=130°,
又∵∠ADE=50°,
∴∠ADB+∠EDC=130°,
∴∠ADB=∠DEC,
又∵AB=DC=4,
在△ABD和△DCE中,
∴△ABD≌△DCE(AAS),
即当DC=4时,△ABD≌△DCE.
(3)可以,100°或115°
【解析】【解答】解:∵在△BAD中,∠B=∠C=∠50°,∠BDA=120°,
∴∠BAD=180°-∠B-∠BDA=180°-50°-120°=10°;
∴∠EDC=180°-∠BDA-∠ADE=180°-120°-50°=10°.
点D从B向C运动时,∠BDA逐渐变小,
故答案为:10,小;
(3)当∠BDA的度数为100°或115°时,△ADE的形状是等腰三角形,
∵∠BDA=100°时,
∴∠ADC=80°,
∵∠C=50°,
∴∠DAC=50°,
∴∠DAC=∠ADE,
∴△ADE的形状是等腰三角形;
∵当∠BDA的度数为115°时,
∴∠ADC=65°,
∵∠C=50°,
∴∠DAC=65°,
∵∠ADE=50°,
∴∠AED=65°,
∴∠DAC=∠AED,
∴△ADE的形状是等腰三角形.
6.【答案】(1)t
(2)证明:∵∠CFD=90°,∠B=90°,
∴DF∥AB,
∴∠AED=∠FDE.
在△AED和△FDE中, ,
∴△AED≌△FDE(SAS).
(3)解:∵△AED≌△FDE,
∴当△DEF是等边三角形时,△EDA是等边三角形.
∵∠A=90°﹣∠C=60°,
∴AD=AE.
∵AE=t,AD=AC﹣CD=10﹣2t,
∴t=10﹣2t,
∴t= ,
∴当t为 时,△DEF是等边三角形.
(4)解:∵△AED≌△FDE,
∴当△DEF为直角三角形时,△EDA是直角三角形.
当∠AED=90°时,AD=2AE,即10﹣2t=2t,
解得:t= ;
当∠ADE=90°时,AE=2AD,即t=2(10﹣2t),
解得:t=4.
综上所述:当t为 或4时,△DEF为直角三角形.
【解析】【解答】解:(1)∵DF⊥BC,
∴∠CFD=90°.
在Rt△CDF中,∠CFD=90°,∠C=30°,CD=2t,
∴DF= CD=t.
故答案为:t.
7.【答案】(1)证明:如图1中,
∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(2)解:如图2中,设AE交CD于O.
∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABD=∠ACE,
∵∠ABC=∠ACB=60°,
∴∠ABD=180° ∠ABC=120°,
∴∠ACE=120°,
∴∠DCE=∠ACE ∠ACB=60°,
∵∠AOC=∠DOE,∠ACO=∠DEO=60°,
∴∠EDC=∠CAO=60° α,
∴∠DEC=180° ∠EDC ∠ECD=180° (60° α) 60°=60°+α
(3)解:如图3中,
∵△ABC,△ADE都是等边三角形,
∴∠ACB=∠B=∠ADE=60°,AC=BC,
∵ED⊥BD,
∴∠EDB=90°,
∴∠ADB=90° 60°=30°,
∴∠BAD=180° ∠B ∠ADB=90°,
∵∠ACB=∠CAD+∠CDA=60°,
∴∠CDA=∠CAD=30°,
∴CA=CD,
∴CB=CD,
∴S△ACD=S△ABC=4,
∵EA=ED,CA=CD,
∴CE垂直平分线段AD,
∴AF=DF,
∴S△ACF= S△ACD=2.
8.【答案】(1)解:∵AE=AB,
∴∠AEB=∠ABE=63°,
∴∠EAB=54°,
∵∠BAC=45°,∠EAF+∠BAC=180°,
∴∠EAB+2∠BAC+∠FAC=180°,
∴54°+2×45°+∠FAC=180°,
∴∠FAC=36°;
(2)解:EF=2AD;理由如下:
延长AD至H,使DH=AD,连接BH,如图1所示:
∵AD为△ABC的中线,
∴BD=CD,
在△BDH和△CDA中, ,
∴△BDH≌△CDA(SAS),
∴HB=AC=AF,∠BHD=∠CAD,
∴AC∥BH,
∴∠ABH+∠BAC=180°,
∵∠EAF+∠BAC=180°,
∴∠EAF=∠ABH,
在△ABH和△EAF中, ,
∴△ABH≌△EAF(SAS),
∴EF=AH=2AD;
(3)解: ;理由如下:
由(2)得,AD= EF,又点G为EF中点,
∴EG=AD,
由(2)△ABH≌△EAF,
∴∠AEG=∠BAD,
在△EAG和△ABD中, ,
∴△EAG≌△ABD(SAS),
∴∠EAG=∠ABC=70°,
∵∠EAF+∠BAC=180°,
∴∠EAB+2∠BAC+∠CAF=180°,
即:70°+2∠BAC+∠CAF=180°,
∴∠BAC+ ∠CAF=55°,
∴∠BAC=55°﹣ ∠CAF,
∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣70°﹣∠ACB=110°﹣∠ACB,
∴55°﹣ ∠CAF=110°﹣∠ACB,
∴∠ACB﹣ ∠CAF=55°.
9.【答案】(1)解:设AP=x,则BQ=x.
∵∠BQD=30°,∠C= 60°,
∴∠QPC= 90°,
∴QC=2PC,即x+6=2(6- x)
解得x=2,
即AP=2.
(2)解: 如图,过点P作PF∥BC,交AB于点F,
∵PF∥BC,
∴∠PFA=∠FPA=∠A= 60°,
∴PF=AP=AF,所以PF= BQ.
又∠BDQ=∠PDF,∠DBQ=∠DFP,
∴△DQB≌△DPF(AAS),
∴DQ= DP,
∴在运动过程中,点D是线段PQ的中点.
(3)解:在运动过程中,线段ED的长不发生变化.
∵PF=AP=AF,PE⊥AF,
∴EF= AF.
又△DQB≌△DPF,
∴DF=DB,即DF= BF,
∴ED= EF+ DF= (AF+ BF)= AB=3.
10.【答案】(1);
(2)解: , .
理由:∵ 和 均为等腰直角三角形, ,
∴ , ,
∴ ,
∴ ,
在 和 中,
∴ ,
∴ , .
∵ 为等腰直角三角形,
∴ .
∵点 , , 在同一直线上,
∴ ,
∴ ,
∴ .
又∵ , ,
∴ ,
∴ ,
∴ .
【解析】【解答】(1)①∵ 和 均为等边三角形,
∴∠ABC=∠BAC= , , ,
∴ ,
∴ .
在 和 中,
∴ ,
∴∠CAD=∠CBE,
∵∠CAE+∠EAB+∠ABC= ,
∴∠EAB+∠ABC+∠CBE= ,即∠EAB+∠ABE= ,
∴∠AEB= (∠EAB+∠ABE)= ,
故答案为: ;
②∵ ,
∴ ,
故答案为: ;
11.【答案】(1)证明:∵ , 于点
∴ ,
∴
又∵ ,
∴ ,
∵ , ,
∴ ,即 平分 ;
(2)解:①∵ ,且 , ∴ 为等腰直角三角形 ∵ , ∴ , 在 和 中, ∵ , ∴ ,即 在 和 中, ∵∴∴
【解析】【解答】解:(2)②根据(2)①的结论:
∴
∵
∴
∴
故答案为: .
12.【答案】(1)解: 和 是等腰三角形,
延长AB至G,使得BG=CF,连接DG
在 和 中,
BG=CF,
,
在 和 中,
DE=DE,
,
(2)解:在CA上截取CG=BE,连接DG
是等腰三角形,
在 和 中,
CG=BE,
在 和 中,
FD=FD,
13.【答案】(1)证明:∵AF平分∠CAE,
∴∠EAF=∠CAF,
∵AB=AC,AB=AE,
∴AE=AC,
在△ACF和△AEF中,
∵AE=AC,∠EAF=∠CAF,AF=AF,
∴△ACF≌△AEF(SAS),
∴∠E=∠ACF,
∵AB=AE,
∴∠E=∠ABE,
∴∠ABE=∠ACF;
(2)解:如图,在BF上截取BM=CF,连接AM,
∵△ACF≌△AEF,
∴EF=CF,∠E=∠ACF=∠ABM,
在△ABM和△ACF中,
∵AB=AC,∠ABM=∠ACF,BM=CF,
∴△ABM≌△ACF(SAS),
∴AM=AF,∠BAM=∠CAF,
∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=60°,
∴∠MAF=∠MAC+∠CAF=∠MAC+∠BAM=∠BAC=60°,
∵AM=AF,
∴△AMF为等边三角形;
(3)解:如图3,延长BA、CF交于N,
∵AE∥BC,
∴∠E=∠EBC,
∵AB=AE,
∴∠ABE=∠E,
∴∠ABF=∠CBF,
∵∠ABC=45°,
∴∠ABF=∠CBF=22.5°,∠ACB=45°,
∴∠BAC=180°-45°-45°=90°,
∴∠ACF=∠ABF=22.5°,
∴∠BFC=180°-22.5°-45°-22.5°=90°,
∴∠BFN=∠BFC=90°,
在△BFN和△BFC中,
∵∠NBF=∠CBF,BF=BF,∠BFN=∠BFC,
∴△BFN≌△BFC(ASA),
∴CF=FN,即CN=2CF=2EF,
∵∠BAC=90°,
∴∠NAC=∠BAD=90°,
在△BAD和△CAN中,
∵∠ABD=∠ACN ,AB=AC,∠BAD=∠CAN,
∴△BAD≌△CAN(ASA),
∴BD=CN,
∴BD=2EF.
14.【答案】(1)解: .
理由:∵ 与 是对顶三角形,
∴ , , ,
∴ ,
,
∴ ,
∴ ;
(2)解: ,且 .
理由:∵ ,
∴ ,
又∵ , ,
∴ ,
∴ , ,
在 中, ,
∴ ,
∴ ,
即 ,
设AC,BD相交于点M,则 ,
∴ ,
综上所述, ,且 ;
(3)证明:∵E为AD的中点,
∴ ,
又∵ , ,
∴ ,
∴ , ,
∴ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,即 .
15.【答案】(1) 和 都是等边三角形,
,
,即 ,
在 和 中, ,
;
(2)由(1)已证: ,
,
是等边三角形,
,
,
又 ,
,
是直角三角形;
(3)由(2)可知, ,
,
由等腰三角形的定义,分以下三种情况:
①当 时, 是等腰三角形,
则 ,
解得 ;
②当 时, 是等腰三角形,
则 ,
解得 ;
③当 时, 是等腰三角形,
则 ,
解得 ;
综上,当 为 或 或 时, 是等腰三角形.
16.【答案】(1)证明:∵ 平分 , , ,
∴ ,且 , ,
在 和 中,
∴ ,
即 ;
(2)证明:在 上截取 ,连接 ,
∵ 平分 ,
∴ ,
在 和 中,
∴ ,
∴ ,
∵ ,
∴ ,
又∵ 于点E,
∴ ,
∴ ;
(3)
【解析】【解答】解:(3)
已知 , , ,
∴ ,
∴ 是直角三角形, ,
由(1)易证明得到 ,
∴ ,
根据(2)易证明得到 ,
设 ,
则 , ,
∴ , ,
由 可得,
,
∴解得 ,
∴ .
17.【答案】(1)
(2)解:(2)如图,
延长 到点 ,使得 ,延长 到点 ,使得 ,分别连接 、 、 和 ,
∵ ,
∴ 为 的垂直平分线,
∴ ,
∴ ,
同理可得 , ,
∵ ,
∴ ,
∴ ,
在 和 中,
,
∴ (SAS),
∴ ,
∵ , , ,
∴ , 分别是 和 的中位线,
∴ , ,
∴ ;
(3) 或
【解析】【解答】解:(1)∵ , ,M为 的中点,
∴ ,
∴EM=CM;
故答案为: ;
(3)如图1,当直线DE过点A且在AB左侧时,
∵∠DBE=∠ABC=30°,AC=4,DE=2,
∴AB=2AC=8,BD=2DE=4,
∴BE= ,
在Rt△ABE中,AE= ,
∴AD= ;
如图2,当直线DE过点A且在AB右侧时,
∵∠DBE=∠ABC=30°,
∴AB=2AC=8,BD=2DE=4,BE= ,
∴AE= ,
∴AD= .
故答案为: 或 .
18.【答案】(1)解:①∵AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵AE平分∠BAC,
∴∠CAE= ,
∵BD⊥AD,
∴∠ADB=90°,
∵∠AEC=∠BED,
∴∠EBD=∠CAE=
②如图所示,
∵CF⊥CD
∴∠FCD=90°,
∵∠ACB=90°,
∴∠ACF+∠FCE=∠BCD+∠FCE,
即∠ACF=∠BCD,
由①得∠EBD=∠CAE=
在△ACF和△BCD中 ,
∴△ACF≌△BCD(ASA),
∴AF=BD,
(2)解:如图所示,过点D作DH⊥AB于点H,
∵AD平分∠BAC,DM⊥AC,DH⊥AB,
∴DM=DH,
由△ACF≌△BCD 得CF=CD
又∵CF⊥CD
∴∠CFD=45°
∵∠CAE
∴∠FCA=22.5°
∴AF=CF 由②得AF=BD
∴DC=DB
在Rt△CDM和Rt△BDH中 ,
∴Rt△CDM≌Rt△BDH(HL),
∴CM=BH,
在Rt△ADM和Rt△ADH中 ,
∴Rt△ADM≌Rt△ADH(HL),
∴AM=AH,
∴AB+AC=AH+BH+AC=AM+CM+AC=AM+AM=2AM
∴AB、AC、AM之间的数量关系为AB+AC=2AM
19.【答案】(1)解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°,
在△ABE和△BCD中,
,
∴△ABE≌△BCD(SAS),
∴∠BAE=∠CBD;
∴∠AFD=∠ABD+∠BAE=∠ABD+∠CBD=∠ABC=60°;
(2)证明:由(1)得:△ABE≌△BCD,
∴∠BAE=∠CBD,AE=BD,
∴∠AFH=∠BAE+∠ABF=∠CBD+∠ABF=∠ABC=60°,
∵AH⊥BD,
∴∠FAH=30°,
∴HF= AF,
∵EF=HD,
∴AF=BH,
∴HF= BH,
∴BF=HF;
(3)解:由(2)得:BH=AF=10,HF= AF=5,BD=AE=AF+EF=12,
∵∠AMB=∠ABM,
∴AB=AM,
∵AH⊥BD,
∴MH=BH=10,
∴BM=2BH=20,
∴DM=BM-BD=20-12=8.
20.【答案】(1)证明:∵CE⊥AE,BD⊥AE,
∴∠AEC=∠ADB=90°,
∵∠BAC=90°,
∴∠ACE+CAE=∠CAE+∠BAD=90°,
∴∠ACE=∠BAD,
在△CAE与△ABD中
∴△CAE≌△ABD(AAS),
∴AE=BD;
(2)解:连接AH
∵AB=AC,BH=CH,
∴∠BAH= ,∠AHB=90°,
∴∠ABH=∠BAH=45°,
∴AH=BH,
∵∠EAH=∠BAH﹣∠BAD=45°﹣∠BAD,
∠DBH=180°﹣∠ADB﹣∠BAD﹣∠ABH=45°﹣∠BAD,
∴∠EAH=∠DBH,
在△AEH与△BDH中
∴△AEH≌△BDH(SAS),
∴EH=DH,∠AHE=∠BHD,
∴∠AHE+∠EHB=∠BHD+∠EHB=90°
即∠EHD=90°,
∴∠EDH=∠DEH= ;
(3)解:过点M作MS⊥FH于点S,过点E作ER⊥FH,交HF的延长线于点R,过点E作ET∥BC,交HR的延长线于点T.
∵DG⊥FH,ER⊥FH,
∴∠DGH=∠ERH=90°,
∴∠HDG+∠DHG=90°
∵∠DHE=90°,
∴∠EHR+∠DHG=90°,
∴∠HDG=∠HER
在△DHG与△HER中
∴△DHG≌△HER (AAS),
∴HG=ER,
∵ET∥BC,
∴∠ETF=∠BHG,∠EHB=∠HET,
∠ETF=∠FHM,
∵∠EHB=∠BHG,
∴∠HET=∠ETF,
∴HE=HT,
在△EFT与△MFH中
,
∴△EFT≌△MFH(AAS),
∴HF=FT,
∴ ,
∴ER=MS,
∴HG=ER=MS,
设GH=6k,FH=5k,则HG=ER=MS=6k,
,
k= ,
∴FH=5 ,
∴HE=HT=2HF=10 .
21.【答案】(1)等边
(2)①△CEF为等腰三角形,
证明:如图2,∵AB=AC,AD=AE,∠BAC=∠DAE,
∴∠ACB=∠ABC,∠EAC=∠DAB,
∴△EAC≌△DAB,
∴∠ECA=∠B,
∴∠ACE=∠ACB,
∵EF∥BC,
∴∠EFC=∠ACB,
∴∠EFC=∠ACE,
∴CE=FE,
∴△EFC为等腰三角形;
②如图③,△EFC为等腰三角形.
当点D在BC延长线上时,以AD为一边在AD的左侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作BC的平行线EF,交直线AC的延长线于点F,连接DE.
证明:∵AB=AC,AD=AE,∠BAC=∠DAE,
∴∠ACB=∠ABC,∠EAC=∠DAB,
∴△EAC≌△DAB,
∴∠ECA=∠DBA,
∴∠ECF=∠ABC,
∵EF∥BC,
∴∠AFE=∠ACB,
又∵∠ABC=∠ACB,
∴∠AFE=∠ECF,
∴EC=EF,
∴△EFC为等腰三角形.
【解析】【解答】解:(1)如图1,∵AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠ACB=∠ABC=60°,∠EAC=∠DAB,
∴△DAB≌△EAC,
∴∠ECA=∠B=60°,
∵EF∥BC,
∴∠EFC=∠ACB=60°,
∵在△EFC中,∠EFC=∠ECF=60°=∠CEF,
∴△EFC为等边三角形,
故答案为:等边;
22.【答案】(1)证明:∵AB=AD+BD=6+4=10,
AC=,
∴AB=AC,
∴ ∠ACB=∠ABC.
(2)解:如图,
①由题意得BM=t,AN=t,则AM=10-t,
当MN∥BC时,AM=AN,
即10﹣t=t,
∴t=5
②当点M在DA上,即4<t≤10时,△MDE为等腰三角形,有3种可能.
如果DE=DM,则t﹣4=5,
∴t=9;
如果ED=EM,则点M运动到点A,
∴t=10;
如果MD=ME=t﹣4,过E作EH⊥AD,在△EHM中
则(t﹣4)2﹣(t﹣7)2=42,
∴t= ;
综上所述,符合要求的t值为9或10或
23.【答案】(1)解:
①如图1,过点F作FM⊥BC于M.作FN⊥AB于N,连接BF,
∵F是角平分线交点,
∴BF也是角平分线,
∴MF=FN,∠DMF=∠ENF=90°,
∵在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠DAC= ∠BAC=15°,
∴∠CDA=75°,
∵∠MFC=45°,∠MFN=120°,
∴∠NFE=15°,
∴∠NEF=75°=∠MDF,
在△DMF和△ENF中,
∠DMF=∠ENF,∠MDF=∠NEF,MF=NF,
∴△DMF≌△ENF(AAS),
∴FE=FD;
②由①知∠BCE=45°,∠CDF=75°,所以∠AFC=120°,因为∠B=60°,所以∠AFC=2∠B.
(2)解:EF=FD仍然成立;
理由如下:
在AC上截取CG=CD,如图2所示,
∵CE是∠BCA的平分线,
∴∠DCF=∠GCF,
在△CFG和△CFD(SAS),,
∴△CFG≌△CFD(SAS),
∴FD=GF.
∵∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=∠BAC,∠FCA=∠ACB,且∠EAF=∠GAF,
∴∠FAC+∠FCA=(∠BAC+∠ACB)=(180°-∠B)=60°,
∴∠AFC=120°,
∴∠CFD=60°=∠CFG,
∴∠AFG=60°,
又∵∠AFE=∠CFD=60°,
∴∠AFE=∠AFG,
在△AFG和△AFE中,,
∴△AFG≌△AFE(ASA),
∴EF=GF,
∴EF=FD.
24.【答案】(1)解:∵OM是∠AOB的角平分线,
∴∠AOC=∠BOC= ∠AOB=60°,
∵CD⊥OA,
∴∠ODC=90°,
∴∠OCD=30°,
∴∠OCE=∠DCE﹣∠OCD=30°,
在Rt△OCD中,OD= OC,同理:OE= OC,
∴OD+OE=OC
(2)解:(1)中结论仍然成立,理由:
过点C作CF⊥OA于F,CG⊥OB于G,如图,
∴∠OFC=∠OGC=90°,
∵∠AOB=120°,
∴∠FCG=60°,
同(1)的方法得,OF= OC,OG= OC,
∴OF+OG=OC,
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,
∴CF=CG,
∵∠DCE=60°,∠FCG=60°,
∴∠DCF=∠ECG,
∴△CFD≌△CGE,
∴DF=EG,
∴OF=OD+DF=OD+EG,OG=OE﹣EG,
∴OF+OG=OD+EG+OE﹣EG=OD+OE,
∴OD+OE=OC
(3)解:(1)中结论不成立,结论为:OE﹣OD=OC,
理由:过点C作CF⊥OA于F,CG⊥OB于G,如图,
∴∠OFC=∠OGC=90°,
∵∠AOB=120°,
∴∠FCG=60°,
同(1)的方法得,OF= OC,OG= OC,
∴OF+OG=OC,
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,
∴CF=CG,
∵∠DCE=60°,∠FCG=60°,
∴∠DCF=∠ECG,
∴△CFD≌△CGE,
∴DF=EG,
∴OF=DF﹣OD=EG﹣OD,
OG=OE﹣EG,
∴OF+OG=EG﹣OD+OE﹣EG=OE﹣OD,
∴OE﹣OD=OC
25.【答案】(1)6
(2)解:∵△ABD和△BCQ是等边三角形,
∴∠ABD=∠CBQ=60°,
∴∠ABC=∠DBQ,
在△CBA和△QBD中,
∴△CBA≌△QBD(SAS),
∴∠BDQ=∠BAC=60°,
∴∠PDO=60°,
∴PD=2DO=6,
∵PD= DC,
∴DC=9,即OC=OD+CD=12,
∴点C的坐标为(12,0)
(3)解:如图3,
以OA为对称轴作等边△ADE,连接EP,并延长EP交x轴于点F.
由(2)得,△AEP≌△ADB,
∴∠AEP=∠ADB=120°,
∴∠OEF=60°,
∴OF=OA=3,
∴点P在直线EF上运动,当OP⊥EF时,OP最小,
∴OP= OF=
则OP的最小值为 .
【解析】【解答】(1)解:作∠DCH=10°,CH交BD的延长线于H,
∵∠BAO=60°,
∴∠ABO=30°,
∴AB=2OA=6,
∵∠BAO=60°,∠BCO=40°,
∴∠ABC=180°﹣60°﹣40°=80°,
∵BD是△ABC的角平分线,
∴∠ABD=∠CBD=40°,
∴∠CBD=∠DCB,∠OBD=40°﹣30°=10°,
∴DB=DC,
在△OBD和△HCD中,
∴△OBD≌△HCD(ASA),
∴OB=HC,
在△AOB和△FHC中,
∴△AOB≌△FHC(ASA),
∴CF=AB=6,
故答案为6
26.【答案】(1)CD=BE
(2)BC=CD+EC;BD2+CD2=2AD2理由如下:∵∠BAC=∠DAE=90°,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,在△BAD和△CAE中, ,∴△BAD≌△CAE,∴BD=CE,∠ACE=∠B,∴∠DCE=90°,∴CE2+CD2=ED2,在Rt△ADE中,AD2+AE2=ED2,又AD=AE,∴BD2+CD2=2AD2;
(3)解:作AE⊥AD,使AE=AD,连接CE,DE,
∵∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE=9,
∵∠ADC=45°,∠EDA=45°,
∴∠EDC=90°,
∴DE= =6 ,
∵∠DAE=90°,
∴AD=AE= DE=6.
【解析】【解答】解:(1)∵△ADB与△AEC为等腰直角三角形
∴∠DAB=90 =∠EAC,
AD=AB ①
AE=AC ②
∴∠CAD=∠DAB+∠BAC=∠EAC+∠BAC=∠BAE ③
综合①②③,可证△ADC≌△ABE,
∴CD=BE
1.(2019八上·越秀期中)已知:在等腰三角形ABC中,AB=AC,AD⊥BC于点D,以AC为边作等边三角形ACE,直线BE交直线AD于点F,连接FC.
(1)如图1,120°<∠BAC<180°,△ACE与△ABC在直线AC的异侧,且FC交AE于点M.
①求证:∠FEA=∠FCA;
②猜想线段FE,AD,FD之间的数量关系,并证明你的结论;
(2)当60°<∠BAC<120°,且△ACE与△ABC在直线AC的异侧时,利用图2画出图形探究线段FE,AD,FD之间的数量关系,并直接写出你的结论.
2.(2019八上·南开期中)如图,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.
(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.
3.问题情境:如图①,在△ABD与△CAE中,BD=AE,∠DBA=∠EAC,AB=AC,易证:△ABD≌△CAE.(不需要证明)
特例探究:如图②,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F.求证:△ABD≌△CAE.
归纳证明:如图③,在等边△ABC中,点D、E分别在边CB、BA的延长线上,且BD=AE.△ABD与△CAE是否全等?如果全等,请证明;如果不全等,请说明理由.
拓展应用:如图④,在等腰三角形中,AB=AC,点O是AB边的垂直平分线与AC的交点,点D、E分别在OB、BA的延长线上.若BD=AE,∠BAC=50°,∠AEC=32°,求∠BAD的度数.
4.如图,已知在△ABC中,AB=AC=10cm,BC=8cm,D为AB中点,设点P在线段BC上以3cm/秒的速度由B点向C点运动,点Q在线段CA上由C点向A点运动.
(1)若Q点运动的速度与P点相同,且点P,Q同时出发,经过1秒钟后△BPD与△CQP是否全等,并说明理由;
(2)若点P,Q同时出发,但运动的速度不相同,当Q点的运动速度为多少时,能在运动过程中有△BPD与△CQP全等?
(3)若点Q以(2)中的速度从点C出发,点P以原来的速度从点B同时出发,都是逆时针沿△ABC的三边上运动,经过多少时间点P与点Q第一次在△ABC的哪条边上相遇?
5.(2021八上·灌云月考)如图,在△ABC中,AB=AC=4,∠B=∠C=50°,点D在线段BC上运动(D不与B,C重合),连接AD,作∠ADE=50°,DE交线段AC于E.
(1)当∠BDA=120°时,∠EDC ;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数,若不可以,请说明理由.
6.(2021八上·温州月考)如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)DF= ;(用含t的代数式表示)
(2)求证:△AED≌△FDE;
(3)当t为何值时,△DEF是等边三角形?说明理由;
(4)当t为何值时,△DEF为直角三角形?(请直接写出t的值.)
7.(2021七下·新都期末)在等边△ABC中,点D是直线BC上的一个点(不与点B、C重合),以AD为边在AD右侧作等边△ADE,连接CE.
(1)如图1,当点D在线段BC上时,求证:BD=CE;
(2)如图2,当点D在线段BC的反向延长线上时,若∠BAE=α,求∠DEC的度数;(用含α的代数式表示)
(3)如图3,当点D在线段BC的延长线上时,若BD⊥DE,且S△ABC=4,求△ACF的面积.
8.(2020八上·章贡期末)已知,如图AD为△ABC的中线,分别以AB和AC为一边在△ABC的外部作等腰三角形ABE和等腰三角形ACF,且AE=AB,AF=AC,连接EF,∠EAF+∠BAC=180°
(1)如图1,若∠ABE=63°,∠BAC=45°,求∠FAC的度数;
(2)如图1请探究线段EF和线段AD有何数量关系?并证明你的结论;
(3)如图2,设EF交AB于点G,交AC于点R,延长FC,EB交于点M,若点G为线段EF的中点,且∠BAE=70°,请探究∠ACB和∠CAF的数量关系,并证明你的结论.
9.()如图所示,△ABC是边长为6的等边三角形,P是AC边上一动点,由点A向点C运动(与A,C不重合),Q是CB延长线上的一点,与点P同时以相同的速度由点B向CB延长线方向运动(Q不与B重合),过点P作PE⊥AB于点E,连接PQ交AB于点D.
(1)当∠BQD=30°时,求AP的长.
(2)试说明:在运动过程中,点D是线段PQ的中点.
(3)在运动过程中,线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化,请说明理由.
10.(2020八上·农安期末)完成下面问题:
(1)问题发现:如图, 和 均为等边三角形,点 , , 在同一直线上,连接 ,填空:① 的度数为 ;②线段 , 之间的数量关系为 ;
(2)拓展探究:如图, 和 均为等腰直角三角形, ,点 , , 在同一直线上, 为 中 边上的高,连接 ,请判断 的度数及线段 , , 之间的数量关系,并说明理由.
11.(2021·孝感模拟)在 中, , 于点 , 为 上一点(不与 , 重合),
(1)如图1,若 ,求证: 平分 ;
(2)如图2,若 ,过点 作 于点 ,交 于 .
①求证: ;
②当 时, 与 的数量关系是▲.
12.(2020八上·沭阳期中)如图①, 和 是等腰三角形,且 , , , ,以 为顶点作一个 角,角的两边分别交边 , 于点 、 ,连接 .
(1)探究 、 、 之间的关系,并说明理由;
(2)若点 、 分别在 、CA延长线上,其他条件不变,如图②所示,则 、 、 之间存在什么样的关系?并说明理由.
13.(2021八上·包河期末)在等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE交DE于点F,连接FC.
(1)如图1,求证:∠ABE=∠ACF;
(2)如图2,当∠ABC=60°时,在BE上取点M,使BM=EF,连接AM.求证:△AFM是等边三角形;
(3)如图3,当∠ABC=45°,且AEBC时,求证:BD=2EF.
14.(2021八上·盐湖期中)定义:顶角相等且顶点重合的两个等腰三角形叫做对顶三角形.如图1,在 OAB与 OCD中,OA=OB,OC=OD,∠AOB=∠COD.
(1)如图1, OAB与 OCD是对顶三角形,且A,O,C三点共线请判断AB与CD的位置关系,并说明理由.
(2)如图2, OAB与 OCD是对顶三角形,∠AOB=∠COD=90°,连接AC,BD,试探究线段AC,BD之间的关系,并说明理由.
(3)如图3, OAB与 OCD是对顶三角形,∠AOB=∠COD=90°,连接AD,BC,取AD的中点E,连接EO并延长交BC于点F,延长OE至点G,使EG=OE,连接AG,求证:EF⊥BC.
15.(2021八上·莒南期中)如图,点 是等边 内的一点, .以 为边作等边 ,使 和 在直线 的同侧,连接 .
(1) 与 全等吗 说明你的理由;
(2)当 时,试判断 的形状,并说明理由;
(3)当 为多少度时, 是等腰三角形 请直接写出答案.
16.(2021八上·江汉期中)如图,在 中, 是角平分线, 于点 , 在边AC上, .
(1)如图1,若 ,求证: ;
(2)如图2,求证: ;
(3)若 , , ,直接写出 的长.
17.(2021·太原模拟)综合与实践
问题背景:数学小组在一次课外学习交流时,组内一同学提出如下问题:在 中, ,D为 边上一点,但不与点B,点C重合,过点D作 于点E.连接 ,M为 的中点,连接 , .
(1)观察发现:如图1, 与 之间的数量关系是 ;
(2)思考分享:如图2,将 绕点B顺时针旋转,其他条件不变,则(1)中的结论还成立,请证明.小明是这样思考的:延长 至点 ,使得 ,连接 运用三角形中位线定理,….按照他的思路或采用其他方法证明;
(3)探究计算:若 , , ,在 绕点B旋转一周的过程中,当直线 经过点A时,线段 的长为 .
18.(2020八上·滨海期末)在 中, , , 平分 交 于点E, 交 延长线于点D,连接 ,过点C作 交 于F.
(1)如图①,①求 的度数;
②求证: ;
(2)如图②, 交 的延长线于点M,探究 之间的数量关系,并给出证明.
19.(2020八上·重庆月考)已知,在等边△ABC 中,D、E 分别为 AC、BC 边上的点,BE=CD,连接 AE、BD 相交于点 F.
(1)如图 1,求∠AFD的度数;
(2)如图 2,过点A作AH⊥BD于H,若EF=HD,求证:BF=HF;
(3)如图 3,在(2)的条件下,延长BD到点M,连接AM,使∠AMB=∠ABM,若EF=2, AF=10,求DM长.
20.(2020八下·成都期中)已知Rt△ABC中,∠BAC=90°,AB=AC,点E为△ABC内一点,连接AE,CE,CE⊥AE,过点B作BD⊥AE,交AE的延长线于D.
(1)如图1,求证BD=AE;
(2)如图2,点H为BC中点,分别连接EH,DH,求∠EDH的度数;
(3)如图3,在(2)的条件下,点M为CH上的一点,连接EM,点F为EM的中点,连接FH,过点D作DG⊥FH,交FH的延长线于点G,若GH:FH=6:5,△FHM的面积为30,∠EHB=∠BHG,求线段EH的长.
21.(2019八上·南平期中)在 中, ,点 为射线 上一个动点(不与 重合),以 为一边在 的右侧作 ,使 , ,过点 作 ,交直线 于点 ,连接 .
(1)如图①,若 ,则按边分类: 是 三角形,并证明;
(2)若 .
①如图②,当点 在线段 上移动时,判断 的形状并证明;
②当点 在线段 的延长线上移动时, 是什么三角形?请在图③中画出相应的图形并直接写出结论(不必证明).
22.(2019八上·江山期中)如图1,△ABC中,CD⊥AB于D,且BD=4,AD=6,CD=8.
(1)求证:∠ACB=∠ABC;
(2)如图2,E为AC的中点,连结DE.动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时另一个点也停止运动.设点M运动的时间为t(秒),
①若MN与BC平行,求t的值;
②问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.
23.(2019七下·西安期末)如图
(1)如图1,在△ABC中,∠ACB是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F,
①请你猜想写出FE与FD之间的数量关系,不用说明理由;
②判断∠AFC与∠B的数量关系,请说明理由.
(2)如图2,在△ABC中,如果∠ACB不是直角,而(1)中其他条件不变,请问你在(1)中所得FE与FD之间的数量关系是否依然成立?请说明理由.
24.如图,已知∠AOB=120°,在∠AOB的平分线OM上有一点C,将一个60°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;
(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?若成立,请给于证明;若不成立,线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
25.如图,在平面直角坐标系中,A(﹣3,0),点B是y轴正半轴上一动点,点C、D在x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长 .
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接QD并延长,交y轴于点P,当点C运动到什么位置时,满足PD= DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在y轴上运动时,求OP的最小值.
26.(1)【问题探究】如图①已知锐角△ABC,分别以AB、AC为腰,在△ABC的外部作等腰Rt△ABD和Rt△ACE,连接CD、BE,是猜想CD、BE的大小关系 ;(不必证明)
(2)【深入探究】如图②△ABC、△ADE都是等腰直角三角形,点D在边BC上(不与B、C重合),连接EC,则线段BC,DC,EC之间满足的等量关系式为 ;(不必证明)线段AD2,BD2,CD2之间满足的等量关系,并证明你的结论;
(3)【拓展应用】如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.
答案与解析
1.【答案】(1)证明:①∵△AEC是等边三角形
∴∠EAC=∠ACE=60°,CE=AC=AE,且AB=AC
∴AB=AE
∴∠ABF=∠AEF
∵AB=AC,AD⊥BC
∴AD是BC的垂直平分线
∴BF=FC,且AF=AF,AB=AC
∴△ABF≌△ACF(SSS)
∴∠ABF=∠ACF
∴∠ACF=∠AEF
②EF=FD+AD
延长AD使DP=AD,连接CP
∵AD=DP,∠ADC=∠PDC,CD=CD
∴△ADC≌△PDC(SAS)
∴AC=CP=CE,∠ACD=∠PCD
∵∠ACF=∠AEF,且∠AMC=∠FME
∴∠EFC=∠EAC=60°
∵BF=CF,且∠EFC=60°
∴∠FCD=30°
∵∠FCA=∠FCD-∠ACD
∴∠FCA=30°-∠ACD
∵∠ECF=∠ECA-∠FCA
∴∠ECF=30°+∠ACD
∵∠FCP=∠FCD+∠DCP
∴∠FCP=30°+∠ACD
∴∠ECF=∠FCP,且FC=FC,CP=CE
∴△ECF≌△FCP(SAS)
∴EF=FP
∴EF=FD+AD
(2)解:连接CF,延长AD使FD=DP,连接CP.
∵△AEC是等边三角形
∴∠EAC=∠ACE=60°,CE=AC=AE,且AB=AC
∴AB=AE
∴∠ABF=∠AEF
∵AB=AC,AD⊥BC
∴AD是BC的垂直平分线
∴BF=FC,且AF=AF,AB=AC
∴△ABF≌△ACF(SSS)
∴∠ABF=∠ACF
∴∠ACF=∠AEF且∠AME=∠CMF
∴∠EAC=∠EFC=60°
∵BF=CF,∠EFC=60°
∴∠FCB=30°
∵FD=DP,∠FDC=∠PDC,CD=CD
∴△FDC≌△PDC(SAS)
∴FC=CP,∠FCD=∠PCD=30°
∴∠FCP=60°=∠ACE
∴∠ACP=∠FCE且CF=CP,AC=CE
∴△ACP≌△ECF(SAS)
∴EF=AP
∴EF=AD+DP=AD+DF.
2.【答案】(1)解:∵在Rt△ABO中,∠BAO=30°,
∴AB=2BO=2.
(2)证明:连接OD,
∵△ABE为等边三角形,
∴AB=AE,∠EAB=60°,
∵∠BAO=30°,作OA的垂直平分线MN交AB的垂线AD于点D,
∴∠DAO=60°.
∴∠EAO=∠NAB
又∵DO=DA,
∴△ADO为等边三角形.
∴DA=AO.
在△ABD与△AEO中,
∵ ,
∴△ABD≌△AEO(SAS).
∴BD=OE.
(3)证明:作EH⊥AB于H.
∵AE=BE,∴AH= AB,
∵BO= AB,∴AH=BO,
在Rt△AEH与Rt△BAO中,
,
∴Rt△AEH≌Rt△BAO(HL),
∴EH=AO=AD.
又∵∠EHF=∠DAF=90°,
在△HFE与△AFD中,
,
∴△HFE≌△AFD(AAS),
∴EF=DF.
∴F为DE的中点.
3.【答案】特例探究:证明:∵△ABC是等边三角形,∴AB=AC,∠DBA=∠EAC=60°,在△ABD与△CAE中, ,∴△ABD≌△CAE(SAS);归纳证明:证明:△ABD与△CAE全等.理由如下:∵△ABC是等边三角形,∴AB=AC,∠ABC=∠BAC=60°,∴∠DBA=∠EAC=120°.在△ABD与△CAE中, ,∴△ABD≌△CAE(SAS);拓展应用:解:∵点O在AB的垂直平分线上,∴OA=OB,∴∠OBA=∠BAC=50°,∴∠EAC=∠DBA.在△ABD与△CAE中, ,∴△ABD≌△CAE(SAS),∴∠BDA=∠AEC=32°,∴∠BAD=∠OBA﹣∠BDA=18°.
4.【答案】(1)解:∵t=1秒,
∴BP=CQ=3×1=3cm,
∵AB=10cm,点D为AB的中点,
∴BD=5cm.
又∵PC=BC﹣BP,BC=8cm,
∴PC=8﹣3=5cm,
∴PC=BD.
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,
∴△BPD≌△CQP(SAS).
(2)解:∵vP≠vQ,∴BP≠CQ,
又∵△BPD≌△CPQ,∠B=∠C,则BP=PC=4cm,CQ=BD=5cm,
∴点P,点Q运动的时间 秒,
∴vQ= cm/秒;
(3)设经过x秒后点P与点Q第一次相遇,
由题意,得 x=3x+2×10,
解得x= .
∴点P共运动了 ×3=80cm.
∴80=56+24=2×28+24,
∴点P、点Q在AB边上相遇,
∴经过 秒点P与点Q第一次在边AB上相遇.
5.【答案】(1)10;小
(2)解:当DC=4时,△ABD≌△DCE,
理由:∵∠C=50°,
∴∠DEC+∠EDC=130°,
又∵∠ADE=50°,
∴∠ADB+∠EDC=130°,
∴∠ADB=∠DEC,
又∵AB=DC=4,
在△ABD和△DCE中,
∴△ABD≌△DCE(AAS),
即当DC=4时,△ABD≌△DCE.
(3)可以,100°或115°
【解析】【解答】解:∵在△BAD中,∠B=∠C=∠50°,∠BDA=120°,
∴∠BAD=180°-∠B-∠BDA=180°-50°-120°=10°;
∴∠EDC=180°-∠BDA-∠ADE=180°-120°-50°=10°.
点D从B向C运动时,∠BDA逐渐变小,
故答案为:10,小;
(3)当∠BDA的度数为100°或115°时,△ADE的形状是等腰三角形,
∵∠BDA=100°时,
∴∠ADC=80°,
∵∠C=50°,
∴∠DAC=50°,
∴∠DAC=∠ADE,
∴△ADE的形状是等腰三角形;
∵当∠BDA的度数为115°时,
∴∠ADC=65°,
∵∠C=50°,
∴∠DAC=65°,
∵∠ADE=50°,
∴∠AED=65°,
∴∠DAC=∠AED,
∴△ADE的形状是等腰三角形.
6.【答案】(1)t
(2)证明:∵∠CFD=90°,∠B=90°,
∴DF∥AB,
∴∠AED=∠FDE.
在△AED和△FDE中, ,
∴△AED≌△FDE(SAS).
(3)解:∵△AED≌△FDE,
∴当△DEF是等边三角形时,△EDA是等边三角形.
∵∠A=90°﹣∠C=60°,
∴AD=AE.
∵AE=t,AD=AC﹣CD=10﹣2t,
∴t=10﹣2t,
∴t= ,
∴当t为 时,△DEF是等边三角形.
(4)解:∵△AED≌△FDE,
∴当△DEF为直角三角形时,△EDA是直角三角形.
当∠AED=90°时,AD=2AE,即10﹣2t=2t,
解得:t= ;
当∠ADE=90°时,AE=2AD,即t=2(10﹣2t),
解得:t=4.
综上所述:当t为 或4时,△DEF为直角三角形.
【解析】【解答】解:(1)∵DF⊥BC,
∴∠CFD=90°.
在Rt△CDF中,∠CFD=90°,∠C=30°,CD=2t,
∴DF= CD=t.
故答案为:t.
7.【答案】(1)证明:如图1中,
∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(2)解:如图2中,设AE交CD于O.
∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABD=∠ACE,
∵∠ABC=∠ACB=60°,
∴∠ABD=180° ∠ABC=120°,
∴∠ACE=120°,
∴∠DCE=∠ACE ∠ACB=60°,
∵∠AOC=∠DOE,∠ACO=∠DEO=60°,
∴∠EDC=∠CAO=60° α,
∴∠DEC=180° ∠EDC ∠ECD=180° (60° α) 60°=60°+α
(3)解:如图3中,
∵△ABC,△ADE都是等边三角形,
∴∠ACB=∠B=∠ADE=60°,AC=BC,
∵ED⊥BD,
∴∠EDB=90°,
∴∠ADB=90° 60°=30°,
∴∠BAD=180° ∠B ∠ADB=90°,
∵∠ACB=∠CAD+∠CDA=60°,
∴∠CDA=∠CAD=30°,
∴CA=CD,
∴CB=CD,
∴S△ACD=S△ABC=4,
∵EA=ED,CA=CD,
∴CE垂直平分线段AD,
∴AF=DF,
∴S△ACF= S△ACD=2.
8.【答案】(1)解:∵AE=AB,
∴∠AEB=∠ABE=63°,
∴∠EAB=54°,
∵∠BAC=45°,∠EAF+∠BAC=180°,
∴∠EAB+2∠BAC+∠FAC=180°,
∴54°+2×45°+∠FAC=180°,
∴∠FAC=36°;
(2)解:EF=2AD;理由如下:
延长AD至H,使DH=AD,连接BH,如图1所示:
∵AD为△ABC的中线,
∴BD=CD,
在△BDH和△CDA中, ,
∴△BDH≌△CDA(SAS),
∴HB=AC=AF,∠BHD=∠CAD,
∴AC∥BH,
∴∠ABH+∠BAC=180°,
∵∠EAF+∠BAC=180°,
∴∠EAF=∠ABH,
在△ABH和△EAF中, ,
∴△ABH≌△EAF(SAS),
∴EF=AH=2AD;
(3)解: ;理由如下:
由(2)得,AD= EF,又点G为EF中点,
∴EG=AD,
由(2)△ABH≌△EAF,
∴∠AEG=∠BAD,
在△EAG和△ABD中, ,
∴△EAG≌△ABD(SAS),
∴∠EAG=∠ABC=70°,
∵∠EAF+∠BAC=180°,
∴∠EAB+2∠BAC+∠CAF=180°,
即:70°+2∠BAC+∠CAF=180°,
∴∠BAC+ ∠CAF=55°,
∴∠BAC=55°﹣ ∠CAF,
∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣70°﹣∠ACB=110°﹣∠ACB,
∴55°﹣ ∠CAF=110°﹣∠ACB,
∴∠ACB﹣ ∠CAF=55°.
9.【答案】(1)解:设AP=x,则BQ=x.
∵∠BQD=30°,∠C= 60°,
∴∠QPC= 90°,
∴QC=2PC,即x+6=2(6- x)
解得x=2,
即AP=2.
(2)解: 如图,过点P作PF∥BC,交AB于点F,
∵PF∥BC,
∴∠PFA=∠FPA=∠A= 60°,
∴PF=AP=AF,所以PF= BQ.
又∠BDQ=∠PDF,∠DBQ=∠DFP,
∴△DQB≌△DPF(AAS),
∴DQ= DP,
∴在运动过程中,点D是线段PQ的中点.
(3)解:在运动过程中,线段ED的长不发生变化.
∵PF=AP=AF,PE⊥AF,
∴EF= AF.
又△DQB≌△DPF,
∴DF=DB,即DF= BF,
∴ED= EF+ DF= (AF+ BF)= AB=3.
10.【答案】(1);
(2)解: , .
理由:∵ 和 均为等腰直角三角形, ,
∴ , ,
∴ ,
∴ ,
在 和 中,
∴ ,
∴ , .
∵ 为等腰直角三角形,
∴ .
∵点 , , 在同一直线上,
∴ ,
∴ ,
∴ .
又∵ , ,
∴ ,
∴ ,
∴ .
【解析】【解答】(1)①∵ 和 均为等边三角形,
∴∠ABC=∠BAC= , , ,
∴ ,
∴ .
在 和 中,
∴ ,
∴∠CAD=∠CBE,
∵∠CAE+∠EAB+∠ABC= ,
∴∠EAB+∠ABC+∠CBE= ,即∠EAB+∠ABE= ,
∴∠AEB= (∠EAB+∠ABE)= ,
故答案为: ;
②∵ ,
∴ ,
故答案为: ;
11.【答案】(1)证明:∵ , 于点
∴ ,
∴
又∵ ,
∴ ,
∵ , ,
∴ ,即 平分 ;
(2)解:①∵ ,且 , ∴ 为等腰直角三角形 ∵ , ∴ , 在 和 中, ∵ , ∴ ,即 在 和 中, ∵∴∴
【解析】【解答】解:(2)②根据(2)①的结论:
∴
∵
∴
∴
故答案为: .
12.【答案】(1)解: 和 是等腰三角形,
延长AB至G,使得BG=CF,连接DG
在 和 中,
BG=CF,
,
在 和 中,
DE=DE,
,
(2)解:在CA上截取CG=BE,连接DG
是等腰三角形,
在 和 中,
CG=BE,
在 和 中,
FD=FD,
13.【答案】(1)证明:∵AF平分∠CAE,
∴∠EAF=∠CAF,
∵AB=AC,AB=AE,
∴AE=AC,
在△ACF和△AEF中,
∵AE=AC,∠EAF=∠CAF,AF=AF,
∴△ACF≌△AEF(SAS),
∴∠E=∠ACF,
∵AB=AE,
∴∠E=∠ABE,
∴∠ABE=∠ACF;
(2)解:如图,在BF上截取BM=CF,连接AM,
∵△ACF≌△AEF,
∴EF=CF,∠E=∠ACF=∠ABM,
在△ABM和△ACF中,
∵AB=AC,∠ABM=∠ACF,BM=CF,
∴△ABM≌△ACF(SAS),
∴AM=AF,∠BAM=∠CAF,
∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=60°,
∴∠MAF=∠MAC+∠CAF=∠MAC+∠BAM=∠BAC=60°,
∵AM=AF,
∴△AMF为等边三角形;
(3)解:如图3,延长BA、CF交于N,
∵AE∥BC,
∴∠E=∠EBC,
∵AB=AE,
∴∠ABE=∠E,
∴∠ABF=∠CBF,
∵∠ABC=45°,
∴∠ABF=∠CBF=22.5°,∠ACB=45°,
∴∠BAC=180°-45°-45°=90°,
∴∠ACF=∠ABF=22.5°,
∴∠BFC=180°-22.5°-45°-22.5°=90°,
∴∠BFN=∠BFC=90°,
在△BFN和△BFC中,
∵∠NBF=∠CBF,BF=BF,∠BFN=∠BFC,
∴△BFN≌△BFC(ASA),
∴CF=FN,即CN=2CF=2EF,
∵∠BAC=90°,
∴∠NAC=∠BAD=90°,
在△BAD和△CAN中,
∵∠ABD=∠ACN ,AB=AC,∠BAD=∠CAN,
∴△BAD≌△CAN(ASA),
∴BD=CN,
∴BD=2EF.
14.【答案】(1)解: .
理由:∵ 与 是对顶三角形,
∴ , , ,
∴ ,
,
∴ ,
∴ ;
(2)解: ,且 .
理由:∵ ,
∴ ,
又∵ , ,
∴ ,
∴ , ,
在 中, ,
∴ ,
∴ ,
即 ,
设AC,BD相交于点M,则 ,
∴ ,
综上所述, ,且 ;
(3)证明:∵E为AD的中点,
∴ ,
又∵ , ,
∴ ,
∴ , ,
∴ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,即 .
15.【答案】(1) 和 都是等边三角形,
,
,即 ,
在 和 中, ,
;
(2)由(1)已证: ,
,
是等边三角形,
,
,
又 ,
,
是直角三角形;
(3)由(2)可知, ,
,
由等腰三角形的定义,分以下三种情况:
①当 时, 是等腰三角形,
则 ,
解得 ;
②当 时, 是等腰三角形,
则 ,
解得 ;
③当 时, 是等腰三角形,
则 ,
解得 ;
综上,当 为 或 或 时, 是等腰三角形.
16.【答案】(1)证明:∵ 平分 , , ,
∴ ,且 , ,
在 和 中,
∴ ,
即 ;
(2)证明:在 上截取 ,连接 ,
∵ 平分 ,
∴ ,
在 和 中,
∴ ,
∴ ,
∵ ,
∴ ,
又∵ 于点E,
∴ ,
∴ ;
(3)
【解析】【解答】解:(3)
已知 , , ,
∴ ,
∴ 是直角三角形, ,
由(1)易证明得到 ,
∴ ,
根据(2)易证明得到 ,
设 ,
则 , ,
∴ , ,
由 可得,
,
∴解得 ,
∴ .
17.【答案】(1)
(2)解:(2)如图,
延长 到点 ,使得 ,延长 到点 ,使得 ,分别连接 、 、 和 ,
∵ ,
∴ 为 的垂直平分线,
∴ ,
∴ ,
同理可得 , ,
∵ ,
∴ ,
∴ ,
在 和 中,
,
∴ (SAS),
∴ ,
∵ , , ,
∴ , 分别是 和 的中位线,
∴ , ,
∴ ;
(3) 或
【解析】【解答】解:(1)∵ , ,M为 的中点,
∴ ,
∴EM=CM;
故答案为: ;
(3)如图1,当直线DE过点A且在AB左侧时,
∵∠DBE=∠ABC=30°,AC=4,DE=2,
∴AB=2AC=8,BD=2DE=4,
∴BE= ,
在Rt△ABE中,AE= ,
∴AD= ;
如图2,当直线DE过点A且在AB右侧时,
∵∠DBE=∠ABC=30°,
∴AB=2AC=8,BD=2DE=4,BE= ,
∴AE= ,
∴AD= .
故答案为: 或 .
18.【答案】(1)解:①∵AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵AE平分∠BAC,
∴∠CAE= ,
∵BD⊥AD,
∴∠ADB=90°,
∵∠AEC=∠BED,
∴∠EBD=∠CAE=
②如图所示,
∵CF⊥CD
∴∠FCD=90°,
∵∠ACB=90°,
∴∠ACF+∠FCE=∠BCD+∠FCE,
即∠ACF=∠BCD,
由①得∠EBD=∠CAE=
在△ACF和△BCD中 ,
∴△ACF≌△BCD(ASA),
∴AF=BD,
(2)解:如图所示,过点D作DH⊥AB于点H,
∵AD平分∠BAC,DM⊥AC,DH⊥AB,
∴DM=DH,
由△ACF≌△BCD 得CF=CD
又∵CF⊥CD
∴∠CFD=45°
∵∠CAE
∴∠FCA=22.5°
∴AF=CF 由②得AF=BD
∴DC=DB
在Rt△CDM和Rt△BDH中 ,
∴Rt△CDM≌Rt△BDH(HL),
∴CM=BH,
在Rt△ADM和Rt△ADH中 ,
∴Rt△ADM≌Rt△ADH(HL),
∴AM=AH,
∴AB+AC=AH+BH+AC=AM+CM+AC=AM+AM=2AM
∴AB、AC、AM之间的数量关系为AB+AC=2AM
19.【答案】(1)解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°,
在△ABE和△BCD中,
,
∴△ABE≌△BCD(SAS),
∴∠BAE=∠CBD;
∴∠AFD=∠ABD+∠BAE=∠ABD+∠CBD=∠ABC=60°;
(2)证明:由(1)得:△ABE≌△BCD,
∴∠BAE=∠CBD,AE=BD,
∴∠AFH=∠BAE+∠ABF=∠CBD+∠ABF=∠ABC=60°,
∵AH⊥BD,
∴∠FAH=30°,
∴HF= AF,
∵EF=HD,
∴AF=BH,
∴HF= BH,
∴BF=HF;
(3)解:由(2)得:BH=AF=10,HF= AF=5,BD=AE=AF+EF=12,
∵∠AMB=∠ABM,
∴AB=AM,
∵AH⊥BD,
∴MH=BH=10,
∴BM=2BH=20,
∴DM=BM-BD=20-12=8.
20.【答案】(1)证明:∵CE⊥AE,BD⊥AE,
∴∠AEC=∠ADB=90°,
∵∠BAC=90°,
∴∠ACE+CAE=∠CAE+∠BAD=90°,
∴∠ACE=∠BAD,
在△CAE与△ABD中
∴△CAE≌△ABD(AAS),
∴AE=BD;
(2)解:连接AH
∵AB=AC,BH=CH,
∴∠BAH= ,∠AHB=90°,
∴∠ABH=∠BAH=45°,
∴AH=BH,
∵∠EAH=∠BAH﹣∠BAD=45°﹣∠BAD,
∠DBH=180°﹣∠ADB﹣∠BAD﹣∠ABH=45°﹣∠BAD,
∴∠EAH=∠DBH,
在△AEH与△BDH中
∴△AEH≌△BDH(SAS),
∴EH=DH,∠AHE=∠BHD,
∴∠AHE+∠EHB=∠BHD+∠EHB=90°
即∠EHD=90°,
∴∠EDH=∠DEH= ;
(3)解:过点M作MS⊥FH于点S,过点E作ER⊥FH,交HF的延长线于点R,过点E作ET∥BC,交HR的延长线于点T.
∵DG⊥FH,ER⊥FH,
∴∠DGH=∠ERH=90°,
∴∠HDG+∠DHG=90°
∵∠DHE=90°,
∴∠EHR+∠DHG=90°,
∴∠HDG=∠HER
在△DHG与△HER中
∴△DHG≌△HER (AAS),
∴HG=ER,
∵ET∥BC,
∴∠ETF=∠BHG,∠EHB=∠HET,
∠ETF=∠FHM,
∵∠EHB=∠BHG,
∴∠HET=∠ETF,
∴HE=HT,
在△EFT与△MFH中
,
∴△EFT≌△MFH(AAS),
∴HF=FT,
∴ ,
∴ER=MS,
∴HG=ER=MS,
设GH=6k,FH=5k,则HG=ER=MS=6k,
,
k= ,
∴FH=5 ,
∴HE=HT=2HF=10 .
21.【答案】(1)等边
(2)①△CEF为等腰三角形,
证明:如图2,∵AB=AC,AD=AE,∠BAC=∠DAE,
∴∠ACB=∠ABC,∠EAC=∠DAB,
∴△EAC≌△DAB,
∴∠ECA=∠B,
∴∠ACE=∠ACB,
∵EF∥BC,
∴∠EFC=∠ACB,
∴∠EFC=∠ACE,
∴CE=FE,
∴△EFC为等腰三角形;
②如图③,△EFC为等腰三角形.
当点D在BC延长线上时,以AD为一边在AD的左侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作BC的平行线EF,交直线AC的延长线于点F,连接DE.
证明:∵AB=AC,AD=AE,∠BAC=∠DAE,
∴∠ACB=∠ABC,∠EAC=∠DAB,
∴△EAC≌△DAB,
∴∠ECA=∠DBA,
∴∠ECF=∠ABC,
∵EF∥BC,
∴∠AFE=∠ACB,
又∵∠ABC=∠ACB,
∴∠AFE=∠ECF,
∴EC=EF,
∴△EFC为等腰三角形.
【解析】【解答】解:(1)如图1,∵AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠ACB=∠ABC=60°,∠EAC=∠DAB,
∴△DAB≌△EAC,
∴∠ECA=∠B=60°,
∵EF∥BC,
∴∠EFC=∠ACB=60°,
∵在△EFC中,∠EFC=∠ECF=60°=∠CEF,
∴△EFC为等边三角形,
故答案为:等边;
22.【答案】(1)证明:∵AB=AD+BD=6+4=10,
AC=,
∴AB=AC,
∴ ∠ACB=∠ABC.
(2)解:如图,
①由题意得BM=t,AN=t,则AM=10-t,
当MN∥BC时,AM=AN,
即10﹣t=t,
∴t=5
②当点M在DA上,即4<t≤10时,△MDE为等腰三角形,有3种可能.
如果DE=DM,则t﹣4=5,
∴t=9;
如果ED=EM,则点M运动到点A,
∴t=10;
如果MD=ME=t﹣4,过E作EH⊥AD,在△EHM中
则(t﹣4)2﹣(t﹣7)2=42,
∴t= ;
综上所述,符合要求的t值为9或10或
23.【答案】(1)解:
①如图1,过点F作FM⊥BC于M.作FN⊥AB于N,连接BF,
∵F是角平分线交点,
∴BF也是角平分线,
∴MF=FN,∠DMF=∠ENF=90°,
∵在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠DAC= ∠BAC=15°,
∴∠CDA=75°,
∵∠MFC=45°,∠MFN=120°,
∴∠NFE=15°,
∴∠NEF=75°=∠MDF,
在△DMF和△ENF中,
∠DMF=∠ENF,∠MDF=∠NEF,MF=NF,
∴△DMF≌△ENF(AAS),
∴FE=FD;
②由①知∠BCE=45°,∠CDF=75°,所以∠AFC=120°,因为∠B=60°,所以∠AFC=2∠B.
(2)解:EF=FD仍然成立;
理由如下:
在AC上截取CG=CD,如图2所示,
∵CE是∠BCA的平分线,
∴∠DCF=∠GCF,
在△CFG和△CFD(SAS),,
∴△CFG≌△CFD(SAS),
∴FD=GF.
∵∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=∠BAC,∠FCA=∠ACB,且∠EAF=∠GAF,
∴∠FAC+∠FCA=(∠BAC+∠ACB)=(180°-∠B)=60°,
∴∠AFC=120°,
∴∠CFD=60°=∠CFG,
∴∠AFG=60°,
又∵∠AFE=∠CFD=60°,
∴∠AFE=∠AFG,
在△AFG和△AFE中,,
∴△AFG≌△AFE(ASA),
∴EF=GF,
∴EF=FD.
24.【答案】(1)解:∵OM是∠AOB的角平分线,
∴∠AOC=∠BOC= ∠AOB=60°,
∵CD⊥OA,
∴∠ODC=90°,
∴∠OCD=30°,
∴∠OCE=∠DCE﹣∠OCD=30°,
在Rt△OCD中,OD= OC,同理:OE= OC,
∴OD+OE=OC
(2)解:(1)中结论仍然成立,理由:
过点C作CF⊥OA于F,CG⊥OB于G,如图,
∴∠OFC=∠OGC=90°,
∵∠AOB=120°,
∴∠FCG=60°,
同(1)的方法得,OF= OC,OG= OC,
∴OF+OG=OC,
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,
∴CF=CG,
∵∠DCE=60°,∠FCG=60°,
∴∠DCF=∠ECG,
∴△CFD≌△CGE,
∴DF=EG,
∴OF=OD+DF=OD+EG,OG=OE﹣EG,
∴OF+OG=OD+EG+OE﹣EG=OD+OE,
∴OD+OE=OC
(3)解:(1)中结论不成立,结论为:OE﹣OD=OC,
理由:过点C作CF⊥OA于F,CG⊥OB于G,如图,
∴∠OFC=∠OGC=90°,
∵∠AOB=120°,
∴∠FCG=60°,
同(1)的方法得,OF= OC,OG= OC,
∴OF+OG=OC,
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,
∴CF=CG,
∵∠DCE=60°,∠FCG=60°,
∴∠DCF=∠ECG,
∴△CFD≌△CGE,
∴DF=EG,
∴OF=DF﹣OD=EG﹣OD,
OG=OE﹣EG,
∴OF+OG=EG﹣OD+OE﹣EG=OE﹣OD,
∴OE﹣OD=OC
25.【答案】(1)6
(2)解:∵△ABD和△BCQ是等边三角形,
∴∠ABD=∠CBQ=60°,
∴∠ABC=∠DBQ,
在△CBA和△QBD中,
∴△CBA≌△QBD(SAS),
∴∠BDQ=∠BAC=60°,
∴∠PDO=60°,
∴PD=2DO=6,
∵PD= DC,
∴DC=9,即OC=OD+CD=12,
∴点C的坐标为(12,0)
(3)解:如图3,
以OA为对称轴作等边△ADE,连接EP,并延长EP交x轴于点F.
由(2)得,△AEP≌△ADB,
∴∠AEP=∠ADB=120°,
∴∠OEF=60°,
∴OF=OA=3,
∴点P在直线EF上运动,当OP⊥EF时,OP最小,
∴OP= OF=
则OP的最小值为 .
【解析】【解答】(1)解:作∠DCH=10°,CH交BD的延长线于H,
∵∠BAO=60°,
∴∠ABO=30°,
∴AB=2OA=6,
∵∠BAO=60°,∠BCO=40°,
∴∠ABC=180°﹣60°﹣40°=80°,
∵BD是△ABC的角平分线,
∴∠ABD=∠CBD=40°,
∴∠CBD=∠DCB,∠OBD=40°﹣30°=10°,
∴DB=DC,
在△OBD和△HCD中,
∴△OBD≌△HCD(ASA),
∴OB=HC,
在△AOB和△FHC中,
∴△AOB≌△FHC(ASA),
∴CF=AB=6,
故答案为6
26.【答案】(1)CD=BE
(2)BC=CD+EC;BD2+CD2=2AD2理由如下:∵∠BAC=∠DAE=90°,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,在△BAD和△CAE中, ,∴△BAD≌△CAE,∴BD=CE,∠ACE=∠B,∴∠DCE=90°,∴CE2+CD2=ED2,在Rt△ADE中,AD2+AE2=ED2,又AD=AE,∴BD2+CD2=2AD2;
(3)解:作AE⊥AD,使AE=AD,连接CE,DE,
∵∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE=9,
∵∠ADC=45°,∠EDA=45°,
∴∠EDC=90°,
∴DE= =6 ,
∵∠DAE=90°,
∴AD=AE= DE=6.
【解析】【解答】解:(1)∵△ADB与△AEC为等腰直角三角形
∴∠DAB=90 =∠EAC,
AD=AB ①
AE=AC ②
∴∠CAD=∠DAB+∠BAC=∠EAC+∠BAC=∠BAE ③
综合①②③,可证△ADC≌△ABE,
∴CD=BE
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
