6.3向心加速度(共17张ppt)
文档属性
| 名称 | 6.3向心加速度(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 558.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-12 07:48:12 | ||
图片预览



文档简介
(共17张PPT)
思考?
物体做曲线运动的条件是什么?
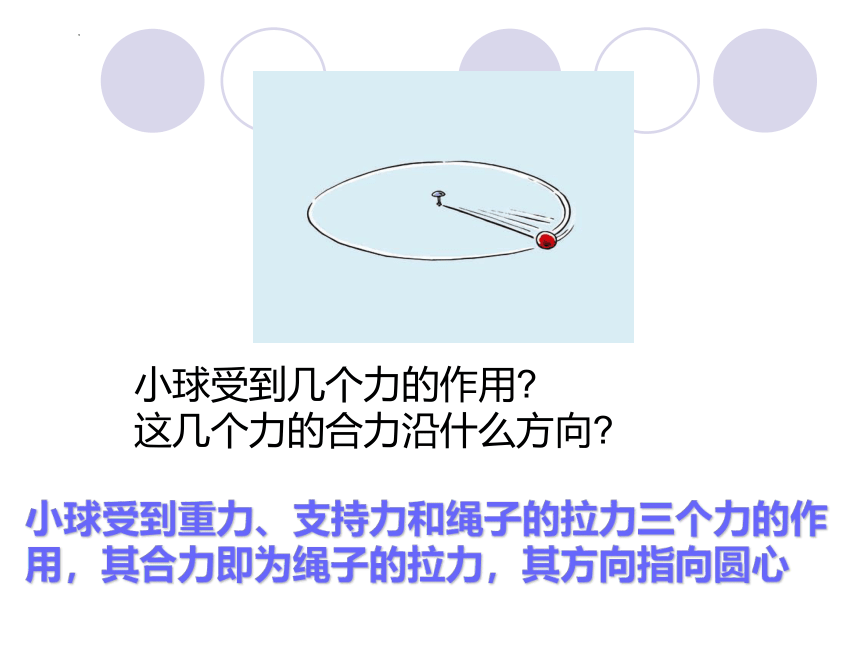
小球受到几个力的作用
这几个力的合力沿什么方向
小球受到重力、支持力和绳子的拉力三个力的作用,其合力即为绳子的拉力,其方向指向圆心
地球受到什么力的作用
这个力可能沿什么方向
应该受到指向太阳的引力作用
向心加速度
“任何物体做匀速圆周运动的加速度都指向圆心”
讨论
一、感知加速度的方向
下面我们要从加速度的定义a = △ v/△t进行一般性的讨论
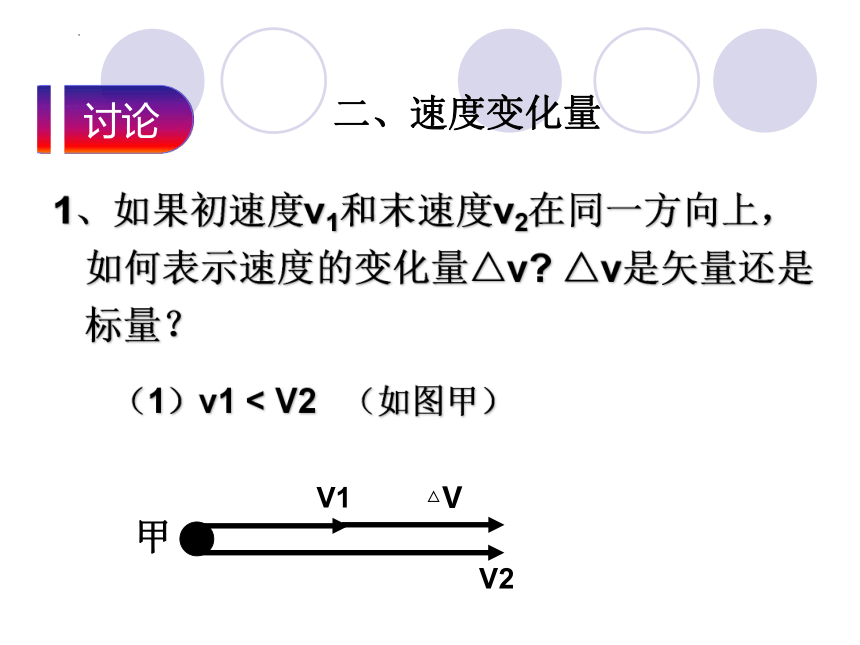
1、如果初速度v1和末速度v2在同一方向上,如何表示速度的变化量△v △v是矢量还是标量?
甲
V1
△V
V2
(1)v1 < V2 (如图甲)
讨论
二、速度变化量
乙
V1
△V
V2
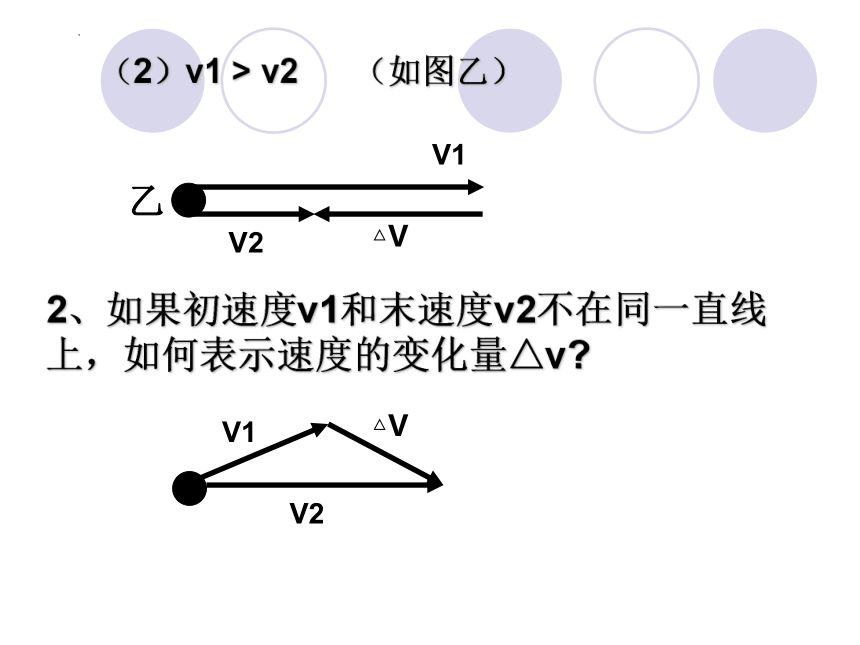
(2)v1 > v2 (如图乙)
2、如果初速度v1和末速度v2不在同一直线上,如何表示速度的变化量△v
V1
△V
V2
速度的变化量
探究:设质点沿半径为r的圆周运动,某时刻位于A点,速度为VA,经过时间后位于B点,速度为VB,质点速度的变化量沿什么方向?
从初速度矢量vA 的末端作一个矢量△v至末速度矢量vB 的末端,矢量△v就等于速度的变化量。
从同一点作出物体在这段时间内的始末两个速度的矢量vA和vB,
讨论
在图丁中,△v的延长线并不通过圆心,为什么说这个加速度是“指向圆心”的
讨论
三、向心加速度
上面的推导不涉及“地球公转“小球绕图钉转动”等具体的运动,结论具有一般性:
做匀速圆周运动的物体加速度指向圆心.这个加速度称为向心加速度.
结论
三、向心加速度的方向
推导
四、向心加速度表达式的推导过程
vA⊥OA,vB⊥OA,且vA=vB=v,OA=OA=r,
所以△AOB与vA、vB、△v组成的矢量三角形相似,
则有:
代入加速度定义式 a =
得:a=
当△t→0时,
即有:△t→0时,
=
= v,
∴ a =
又∵v=ωr
∴又有 a =ω2r 或 a =ωv
an=v2/r , an=rω2
分析
三、向心加速度的大小
讨论
正确认识向心加速度的两种表达式
下列关于向心加速度的说法中,正确的是 ( )
A.向心加速度的方向始终与速度的方向垂直 B.向心加速度的方向保持不变
C.在匀速圆周运动中,向心加速度是恒定的
D.在匀速圆周运动中,向心加速度的大小不断变化
练习
A
如图6.6—10所示,长度为L=0.5m的轻杆,一端固定质量为M=1.0kg的小球A(小球的半径不计),另一端固定在一转动轴O上.小球绕轴在水平面上匀速转动的过程中,每隔0.1s杆转过的角度为30°.试求:小球运动的向心加速度.
练习
14 m/S2
一、感知做匀速圆周运动的物体加速度的方向
二、速度变化量的求法
三、向心加速度
(1)名称的由来
(2)表达式:an=v2/r , an=rω2
(3)对两种表达式的比较、分析
小结
通过本节课的学习我们知道
思考?
物体做曲线运动的条件是什么?
小球受到几个力的作用
这几个力的合力沿什么方向
小球受到重力、支持力和绳子的拉力三个力的作用,其合力即为绳子的拉力,其方向指向圆心
地球受到什么力的作用
这个力可能沿什么方向
应该受到指向太阳的引力作用
向心加速度
“任何物体做匀速圆周运动的加速度都指向圆心”
讨论
一、感知加速度的方向
下面我们要从加速度的定义a = △ v/△t进行一般性的讨论
1、如果初速度v1和末速度v2在同一方向上,如何表示速度的变化量△v △v是矢量还是标量?
甲
V1
△V
V2
(1)v1 < V2 (如图甲)
讨论
二、速度变化量
乙
V1
△V
V2
(2)v1 > v2 (如图乙)
2、如果初速度v1和末速度v2不在同一直线上,如何表示速度的变化量△v
V1
△V
V2
速度的变化量
探究:设质点沿半径为r的圆周运动,某时刻位于A点,速度为VA,经过时间后位于B点,速度为VB,质点速度的变化量沿什么方向?
从初速度矢量vA 的末端作一个矢量△v至末速度矢量vB 的末端,矢量△v就等于速度的变化量。
从同一点作出物体在这段时间内的始末两个速度的矢量vA和vB,
讨论
在图丁中,△v的延长线并不通过圆心,为什么说这个加速度是“指向圆心”的
讨论
三、向心加速度
上面的推导不涉及“地球公转“小球绕图钉转动”等具体的运动,结论具有一般性:
做匀速圆周运动的物体加速度指向圆心.这个加速度称为向心加速度.
结论
三、向心加速度的方向
推导
四、向心加速度表达式的推导过程
vA⊥OA,vB⊥OA,且vA=vB=v,OA=OA=r,
所以△AOB与vA、vB、△v组成的矢量三角形相似,
则有:
代入加速度定义式 a =
得:a=
当△t→0时,
即有:△t→0时,
=
= v,
∴ a =
又∵v=ωr
∴又有 a =ω2r 或 a =ωv
an=v2/r , an=rω2
分析
三、向心加速度的大小
讨论
正确认识向心加速度的两种表达式
下列关于向心加速度的说法中,正确的是 ( )
A.向心加速度的方向始终与速度的方向垂直 B.向心加速度的方向保持不变
C.在匀速圆周运动中,向心加速度是恒定的
D.在匀速圆周运动中,向心加速度的大小不断变化
练习
A
如图6.6—10所示,长度为L=0.5m的轻杆,一端固定质量为M=1.0kg的小球A(小球的半径不计),另一端固定在一转动轴O上.小球绕轴在水平面上匀速转动的过程中,每隔0.1s杆转过的角度为30°.试求:小球运动的向心加速度.
练习
14 m/S2
一、感知做匀速圆周运动的物体加速度的方向
二、速度变化量的求法
三、向心加速度
(1)名称的由来
(2)表达式:an=v2/r , an=rω2
(3)对两种表达式的比较、分析
小结
通过本节课的学习我们知道
