2021-2022学年人教版数学八年级下册17.2勾股定理的逆定理课后练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册17.2勾股定理的逆定理课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 519.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 10:51:12 | ||
图片预览



文档简介
勾股定理的逆定理
一、单选题
1.下列几组线段中,不能组成直角三角形的是( )
A.5,12,13 B.6,8,10 C.7,24,25 D.8,25,27
2.如图,在方格中作以为一边的,要求点也在格点上,这样的能做出( )
A.个 B.个 C. 个 D.个
3.在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB的距离为5,且△ABC是直角三角形,则满足条件的C点有( )
A.4个 B.5个 C.6个 D.8个
4.如果的三边分别为,且满足,则的面积为( )
A.6 B.8 C.10 D.12
5.如图,在四边形中,,,,,.则的大小为( )
A. B. C. D.
6.在中,,,的对边分别是a,b,c,且,则( )
A. B. C. D.不确定哪个角是直角
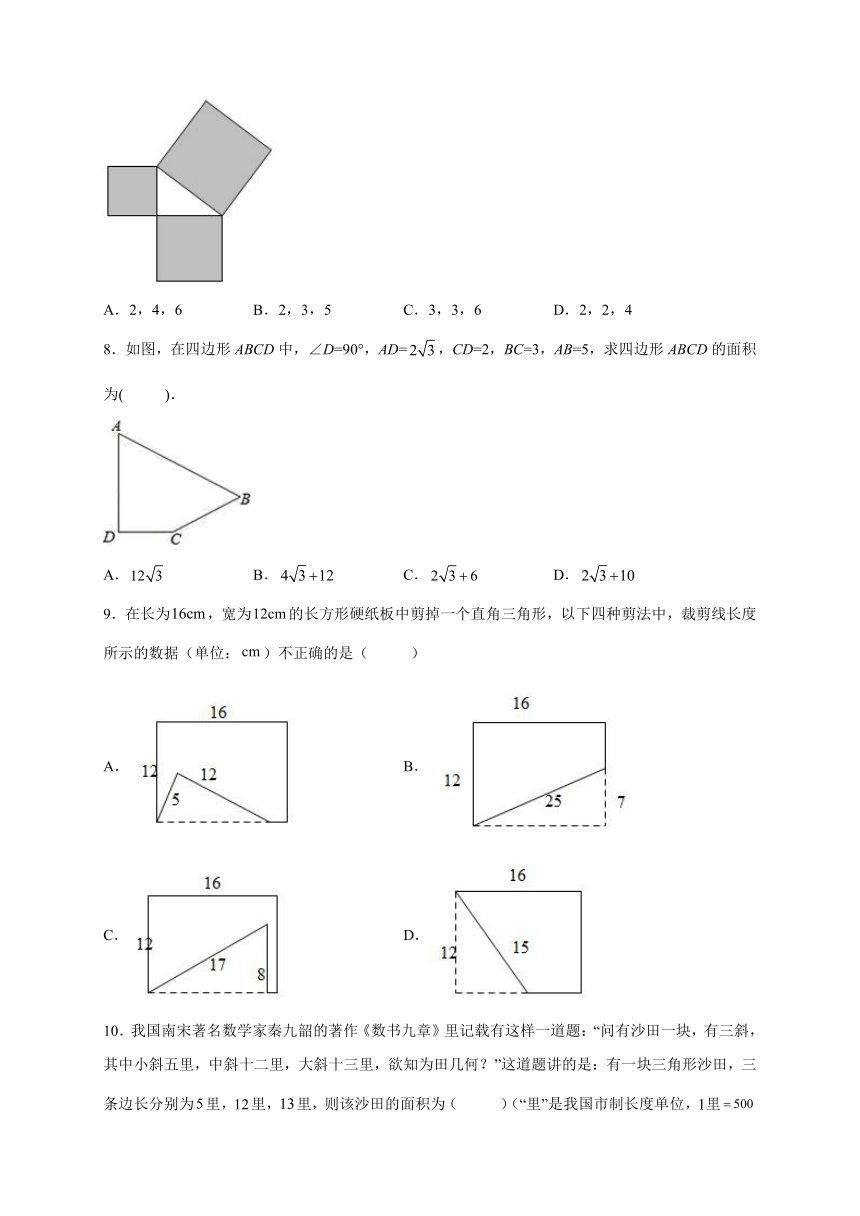
7.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是2,3,4,5,6,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
A.2,4,6 B.2,3,5 C.3,3,6 D.2,2,4
8.如图,在四边形ABCD中,∠D=90°,AD=,CD=2,BC=3,AB=5,求四边形ABCD的面积为( ).
A. B. C. D.
9.在长为,宽为的长方形硬纸板中剪掉一个直角三角形,以下四种剪法中,裁剪线长度所示的数据(单位:)不正确的是( )
A. B.
C. D.
10.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为里,里,里,则该沙田的面积为( )(“里”是我国市制长度单位,里米)
A.平方千米 B.平方千米 C.平方千米 D.平方千米
11.甲、乙两艘轮船同时从港口出发,甲以16海里/时的速度向北偏东的方向航行,它们出发1.5小时后,两船相距30海里,若乙以12海里/时的速度航行,则它的航行方向为( )
A.北偏西 B.南偏西75°
C.南偏东或北偏西 D.南偏西或北偏东
12.已知,,是三角形的三边长,且,那么此三角形是( )
A.以为斜边的直角三角形 B.以为斜边的直角三角形
C.等腰直角三角形 D.锐角三角形
13.如图,在△ABC中,AB=12,BC=13,AC=5,则BC边上的高AD为( )
A.3 B.4 C. D.4.8
14.已知△ABC,AB=5,BC=12,AC=13,点P是AC上一个动点,则线段BP长的最小值是( )
A. B.5 C. D.12
15.在海面上有两个疑似漂浮目标. 接到消息后,A舰艇以12海里/时的速度离开港口O,向北偏西50°方向航行. 同时,B舰艇在同地以16海里/时的速度向北偏东方向行驶,如图所示,离开港口1.5小时后两船相距30海里,则B舰艇的航行方向是( )
A.北偏东60° B.北偏东50° C.北偏东40° D.北偏东30°
二、填空题
16.杜老师要画一个三角形,画好后量得三边长分别为7cm,24cm和25cm,则这个三角形_______(填“是”或“不是”)直角三角形.
17.禅城区某一中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,,若每种植1平方米草皮需要300元,总共需投入______元
18.如图,在四边形中,为的中点,于点,,,,,则四边形的面积为_____.
19.如图,点D在△ABC内,∠BDC=90°,AB=3,AC=BD=2,CD=1,则图中阴影部分的面积为 _______________.
20.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交边BC于点DE,E,F分别是AD,AC上的点,连接CE,EF.若AB=10,BC=6,AC=8,则CE+EF的最小值是________.
三、解答题
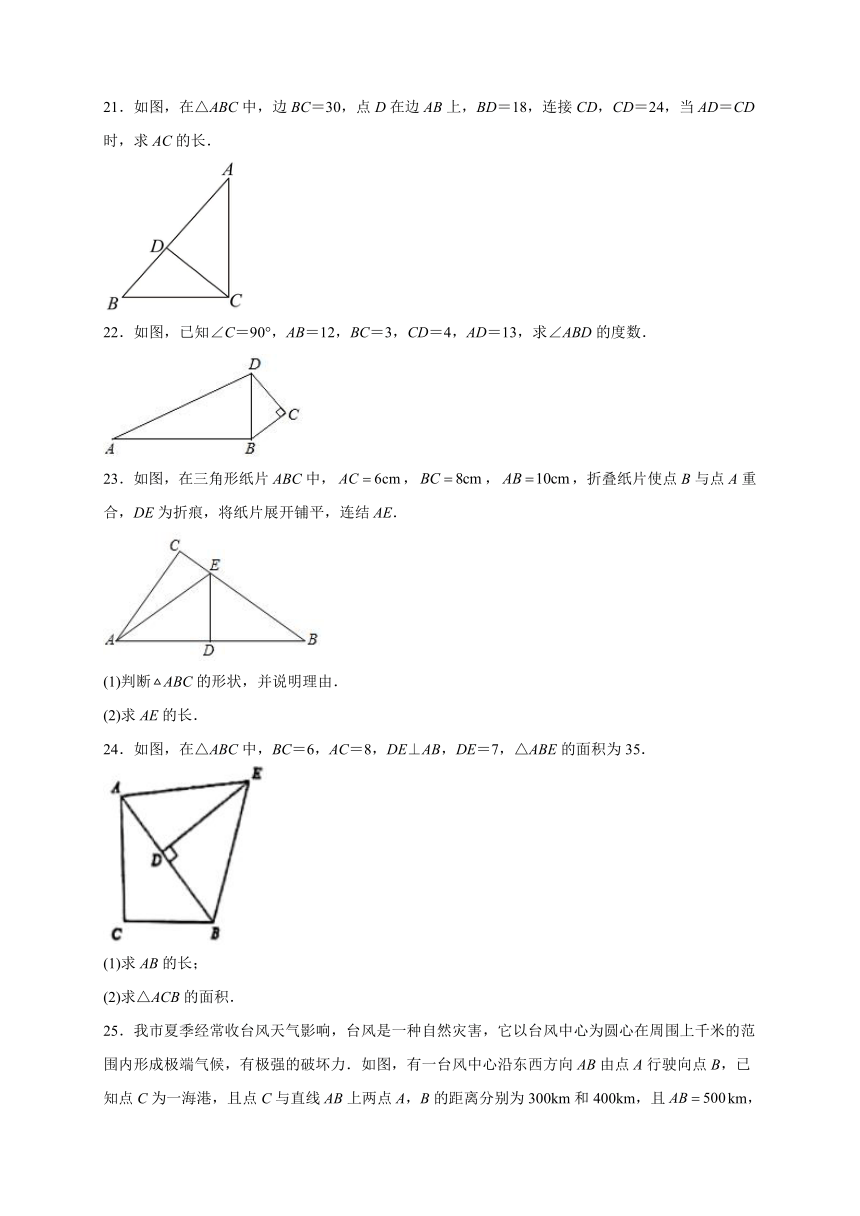
21.如图,在△ABC中,边BC=30,点D在边AB上,BD=18,连接CD,CD=24,当AD=CD时,求AC的长.
22.如图,已知∠C=90°,AB=12,BC=3,CD=4,AD=13,求∠ABD的度数.
23.如图,在三角形纸片ABC中,,,,折叠纸片使点B与点A重合,DE为折痕,将纸片展开铺平,连结AE.
(1)判断ABC的形状,并说明理由.
(2)求AE的长.
24.如图,在△ABC中,BC=6,AC=8,DE⊥AB,DE=7,△ABE的面积为35.
(1)求AB的长;
(2)求△ACB的面积.
25.我市夏季经常收台风天气影响,台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300km和400km,且km,以台风中心为圆心周围250km以内为受影响区域.
(1)求证:;
(2)海港C受台风影响吗?为什么?
(3)若台风的速度为40km/h,则台风影响该海港持续的时间有多长?
试卷第1页,共3页
参考答案:
1.D
解:A、52+122=132,即能组成直角三角形,故本选项不合题意;
B、62+82=102,即能组成直角三角形,故本选项不合题意;
C、72+242=252,即能组成直角三角形,故本选项不合题意;
D、82+252≠272,即不能组成直角三角形,故本选项符合题意;
故选:D.
2.D
解:当AB是斜边时,则第三个顶点所在的位置有:C、D,E,H四个;
当AB是直角边,A是直角顶点时,第三个顶点是F点;
当AB是直角边,B是直角顶点时,第三个顶点是G.
因而共有6个满足条件的顶点.
故选D.
3.C
解:∵点A,B的纵坐标相等,
∴AB∥x轴,
∵点C到AB距离为5,AB=10,
∴点C在平行于AB的两条直线上,
∴过点A的垂线与那两条直线有2个交点,过点B的垂线与那两条直线有2个交点,以AB为直径的圆与那两条直线有只有2个交点(这两个两点在线段AB的垂直平分线上),
∴满足条件的C点共,6个.
故选C.
4.A
解:,
,
,
,
又,
,
为直角三角形,
,
故选:A.
5.D
解:如图,连接AC,
∵,
在Rt△ABC中,由勾股定理得:
AC2=
=
=8
∵,
AD2+AC2
=8+1
=9
而CD2=32=9
∴AD2+AC2=CD2
∴∠CAD=90°,
∠D+∠ACD=90°
∵,
∴∠BAC=∠ACB=45°
∵
∴∠ACD=90°-
∴∠BCD=∠ACB+∠ACD
=45°+(90°-)
=135°-α
故选D
6.A
解:∵在中,,,的对边分别是a,b,c,且,
∴.
∴b、c是两直角边,a是斜边,
∴.
故选:A.
7.C
解:当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是;
当选取的三块纸片的面积分别是2,4,6时,围成的直角三角形的面积是;
当选取的三块纸片的面积分别是3,3,6时,围成的三角形面积是;
当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是,
∵,
因为当选取2,3,4;2,3,6;3,4,5;4,5,6;四种情况时,都不能构成直角三角形,
∴要使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是3,3,6.
故选:C.
8.C
解:∵连接AC,如图所示:
∵∠D=90°,AD=,CD=2,
∴AC==4.
∵BC=3,AB=5,32+42=52,
∴△ABC是直角三角形,∠ACB=90°,
∴S四边形ABCD=S△ACD+S△ABC=××2+×4×3=+6.
故答案选C
9.B
解:A.,
,
故A不符合题意;
B.
,
故B符合题意;
C.
,
故C不符合题意;
D.
,
故D不符合题意,
故选:B.
10.A
解:∵,
,
∴三条边长分别为5里,12里,13里,构成了直角三角形,
∴这块沙田面积为:×5×500×12×500=7500000(平方米)=7.5(平方千米).
故选A.
11.C
解:出发1.5小时后,甲船航行的路程是16×1.5=24海里,乙船航行的路程是12×1.5=18海里;
∵,
∴乙船的航行方向与甲船的航行方向垂直,
∵甲船的航行方向是北偏东75°,
∴乙船的航行方向是南偏东15°或北偏西15°.
故选:C.
12.B
解:∵,
根据绝对值、偶次方的非负性质,
∴c =13,b=12,a=5,
∵52+122=132,
∴△ABC是以c为斜边的直角三角形.
故选B.
13.C
解:,
,
是直角三角形,
,
,
.
故选:.
14.A
解:∵AB=5,BC=12,AC=13,∴AB2+BC2=169=AC2,∴△ABC是直角三角形,当BP⊥AC时,BP最小,∴线段BP长的最小值是:13BP=5×12,解得:BP=.故选A.
点睛:本题主要考查勾股定理的逆定理以及直角三角形面积求法,关键是熟练运用勾股定理的逆定理进行分析.
15.C
解:由题意,得:AB=30海里,
OA=12×1.5=18(海里),
OB=16×1.5=24(海里),
∵OA2+OB2=182+242=900,
AB2=302=900,
∴OA2+OB2= AB2,
∴∠AOB=90°,
∵A舰艇向北偏西50°方向航行,
∴B舰艇的航行方向为北偏东40°.
故选C.
16.是
解:∵三边长分别为7cm,24cm和25cm,,
∴这个三角形是直角三角形,
故答案为:是.
17.10800
解:在中,
∵,
∴AC=5.
在中,,,
而,
即,
∴,
即:
=.
所以需费用:(元).
故答案为10800.
18.##
解:连接,
为的中点,,
∴DE是AB的垂直平分线,,
∵,
,
,
,
,,
,
是直角三角形,
四边形的面积
,
故答案为:.
19.##
解:,,,
,
,,
,
是直角三角形,,
阴影,
故答案为:.
20.4.8##245
解:如图所示:在AB上取点,使,过点C作,垂足为H.
∵AB=10,BC=6,AC=8,
∴
∴是直角三角形,且
∴
∴,
∵,
∴当C、E、共线,且点与H重合时,的值最小,最小值为4.8,
故答案为:4.8.
21.
解:
为直角三角形,
在中
22.90°
解:在直角△BCD中,∠C=90°,BC=3,CD=4,
∴BD=5,
在△ABD中,AD2=132=169,AB2+BD2=122+52=144+25=169,
∴AD2=AB2+BD2,
∴△ABD是直角三角形,
∴∠ABD=90°.
23.(1)直角三角形,见解析
(2)cm
(1)
解:△ABC为直角三角形,理由如下:
∵,,,
∴,
∴△ABC为直角三角形.
(2)
解:折叠纸片点B与点A重合,DE为折痕,
∴,
设,则,
在Rt△ACE中由勾股定理得,,
解得:.
∴.
24.(1)AB=10
(2)24
(1)
解:∵△ABE的面积为35,DE=7,DE⊥AB,
∴AB×7=35,
解得:AB=10;
(2)
解:在△ABC中,AB2=102=100,AC2+BC2=62+82=100,
则AB2=AC2+BC2,
∴∠C=90°,
∴S△ABC=AC BC=×6×8=24,
答:△ACB的面积24.
25.(1)见解析
(2)海港C受台风影响,理由见解析
(3)3.5h
(1)
解:∵km,km,km,
∴.
∴是直角三角形,
∴;
(2)
解:海港C受台风影响.理由如下:
如图,过点C作于D.
∵,
∴.
∵,
∴海港C受到台风影响.
(3)
解:如图,在线段AB上取点E,F,使km,km,则台风中心在线段EF上时正好影响C港口.
∴EC=FC,
∵CD⊥AB,
∴ED=FD,
在中,由勾股定理得:
,
∴km,
∵台风的速度为40km/h,
∴.
∴台风影响该海港持续的时间为3.5h .
答案第1页,共2页
一、单选题
1.下列几组线段中,不能组成直角三角形的是( )
A.5,12,13 B.6,8,10 C.7,24,25 D.8,25,27
2.如图,在方格中作以为一边的,要求点也在格点上,这样的能做出( )
A.个 B.个 C. 个 D.个
3.在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB的距离为5,且△ABC是直角三角形,则满足条件的C点有( )
A.4个 B.5个 C.6个 D.8个
4.如果的三边分别为,且满足,则的面积为( )
A.6 B.8 C.10 D.12
5.如图,在四边形中,,,,,.则的大小为( )
A. B. C. D.
6.在中,,,的对边分别是a,b,c,且,则( )
A. B. C. D.不确定哪个角是直角
7.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是2,3,4,5,6,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
A.2,4,6 B.2,3,5 C.3,3,6 D.2,2,4
8.如图,在四边形ABCD中,∠D=90°,AD=,CD=2,BC=3,AB=5,求四边形ABCD的面积为( ).
A. B. C. D.
9.在长为,宽为的长方形硬纸板中剪掉一个直角三角形,以下四种剪法中,裁剪线长度所示的数据(单位:)不正确的是( )
A. B.
C. D.
10.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为里,里,里,则该沙田的面积为( )(“里”是我国市制长度单位,里米)
A.平方千米 B.平方千米 C.平方千米 D.平方千米
11.甲、乙两艘轮船同时从港口出发,甲以16海里/时的速度向北偏东的方向航行,它们出发1.5小时后,两船相距30海里,若乙以12海里/时的速度航行,则它的航行方向为( )
A.北偏西 B.南偏西75°
C.南偏东或北偏西 D.南偏西或北偏东
12.已知,,是三角形的三边长,且,那么此三角形是( )
A.以为斜边的直角三角形 B.以为斜边的直角三角形
C.等腰直角三角形 D.锐角三角形
13.如图,在△ABC中,AB=12,BC=13,AC=5,则BC边上的高AD为( )
A.3 B.4 C. D.4.8
14.已知△ABC,AB=5,BC=12,AC=13,点P是AC上一个动点,则线段BP长的最小值是( )
A. B.5 C. D.12
15.在海面上有两个疑似漂浮目标. 接到消息后,A舰艇以12海里/时的速度离开港口O,向北偏西50°方向航行. 同时,B舰艇在同地以16海里/时的速度向北偏东方向行驶,如图所示,离开港口1.5小时后两船相距30海里,则B舰艇的航行方向是( )
A.北偏东60° B.北偏东50° C.北偏东40° D.北偏东30°
二、填空题
16.杜老师要画一个三角形,画好后量得三边长分别为7cm,24cm和25cm,则这个三角形_______(填“是”或“不是”)直角三角形.
17.禅城区某一中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,,若每种植1平方米草皮需要300元,总共需投入______元
18.如图,在四边形中,为的中点,于点,,,,,则四边形的面积为_____.
19.如图,点D在△ABC内,∠BDC=90°,AB=3,AC=BD=2,CD=1,则图中阴影部分的面积为 _______________.
20.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交边BC于点DE,E,F分别是AD,AC上的点,连接CE,EF.若AB=10,BC=6,AC=8,则CE+EF的最小值是________.
三、解答题
21.如图,在△ABC中,边BC=30,点D在边AB上,BD=18,连接CD,CD=24,当AD=CD时,求AC的长.
22.如图,已知∠C=90°,AB=12,BC=3,CD=4,AD=13,求∠ABD的度数.
23.如图,在三角形纸片ABC中,,,,折叠纸片使点B与点A重合,DE为折痕,将纸片展开铺平,连结AE.
(1)判断ABC的形状,并说明理由.
(2)求AE的长.
24.如图,在△ABC中,BC=6,AC=8,DE⊥AB,DE=7,△ABE的面积为35.
(1)求AB的长;
(2)求△ACB的面积.
25.我市夏季经常收台风天气影响,台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300km和400km,且km,以台风中心为圆心周围250km以内为受影响区域.
(1)求证:;
(2)海港C受台风影响吗?为什么?
(3)若台风的速度为40km/h,则台风影响该海港持续的时间有多长?
试卷第1页,共3页
参考答案:
1.D
解:A、52+122=132,即能组成直角三角形,故本选项不合题意;
B、62+82=102,即能组成直角三角形,故本选项不合题意;
C、72+242=252,即能组成直角三角形,故本选项不合题意;
D、82+252≠272,即不能组成直角三角形,故本选项符合题意;
故选:D.
2.D
解:当AB是斜边时,则第三个顶点所在的位置有:C、D,E,H四个;
当AB是直角边,A是直角顶点时,第三个顶点是F点;
当AB是直角边,B是直角顶点时,第三个顶点是G.
因而共有6个满足条件的顶点.
故选D.
3.C
解:∵点A,B的纵坐标相等,
∴AB∥x轴,
∵点C到AB距离为5,AB=10,
∴点C在平行于AB的两条直线上,
∴过点A的垂线与那两条直线有2个交点,过点B的垂线与那两条直线有2个交点,以AB为直径的圆与那两条直线有只有2个交点(这两个两点在线段AB的垂直平分线上),
∴满足条件的C点共,6个.
故选C.
4.A
解:,
,
,
,
又,
,
为直角三角形,
,
故选:A.
5.D
解:如图,连接AC,
∵,
在Rt△ABC中,由勾股定理得:
AC2=
=
=8
∵,
AD2+AC2
=8+1
=9
而CD2=32=9
∴AD2+AC2=CD2
∴∠CAD=90°,
∠D+∠ACD=90°
∵,
∴∠BAC=∠ACB=45°
∵
∴∠ACD=90°-
∴∠BCD=∠ACB+∠ACD
=45°+(90°-)
=135°-α
故选D
6.A
解:∵在中,,,的对边分别是a,b,c,且,
∴.
∴b、c是两直角边,a是斜边,
∴.
故选:A.
7.C
解:当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是;
当选取的三块纸片的面积分别是2,4,6时,围成的直角三角形的面积是;
当选取的三块纸片的面积分别是3,3,6时,围成的三角形面积是;
当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是,
∵,
因为当选取2,3,4;2,3,6;3,4,5;4,5,6;四种情况时,都不能构成直角三角形,
∴要使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是3,3,6.
故选:C.
8.C
解:∵连接AC,如图所示:
∵∠D=90°,AD=,CD=2,
∴AC==4.
∵BC=3,AB=5,32+42=52,
∴△ABC是直角三角形,∠ACB=90°,
∴S四边形ABCD=S△ACD+S△ABC=××2+×4×3=+6.
故答案选C
9.B
解:A.,
,
故A不符合题意;
B.
,
故B符合题意;
C.
,
故C不符合题意;
D.
,
故D不符合题意,
故选:B.
10.A
解:∵,
,
∴三条边长分别为5里,12里,13里,构成了直角三角形,
∴这块沙田面积为:×5×500×12×500=7500000(平方米)=7.5(平方千米).
故选A.
11.C
解:出发1.5小时后,甲船航行的路程是16×1.5=24海里,乙船航行的路程是12×1.5=18海里;
∵,
∴乙船的航行方向与甲船的航行方向垂直,
∵甲船的航行方向是北偏东75°,
∴乙船的航行方向是南偏东15°或北偏西15°.
故选:C.
12.B
解:∵,
根据绝对值、偶次方的非负性质,
∴c =13,b=12,a=5,
∵52+122=132,
∴△ABC是以c为斜边的直角三角形.
故选B.
13.C
解:,
,
是直角三角形,
,
,
.
故选:.
14.A
解:∵AB=5,BC=12,AC=13,∴AB2+BC2=169=AC2,∴△ABC是直角三角形,当BP⊥AC时,BP最小,∴线段BP长的最小值是:13BP=5×12,解得:BP=.故选A.
点睛:本题主要考查勾股定理的逆定理以及直角三角形面积求法,关键是熟练运用勾股定理的逆定理进行分析.
15.C
解:由题意,得:AB=30海里,
OA=12×1.5=18(海里),
OB=16×1.5=24(海里),
∵OA2+OB2=182+242=900,
AB2=302=900,
∴OA2+OB2= AB2,
∴∠AOB=90°,
∵A舰艇向北偏西50°方向航行,
∴B舰艇的航行方向为北偏东40°.
故选C.
16.是
解:∵三边长分别为7cm,24cm和25cm,,
∴这个三角形是直角三角形,
故答案为:是.
17.10800
解:在中,
∵,
∴AC=5.
在中,,,
而,
即,
∴,
即:
=.
所以需费用:(元).
故答案为10800.
18.##
解:连接,
为的中点,,
∴DE是AB的垂直平分线,,
∵,
,
,
,
,,
,
是直角三角形,
四边形的面积
,
故答案为:.
19.##
解:,,,
,
,,
,
是直角三角形,,
阴影,
故答案为:.
20.4.8##245
解:如图所示:在AB上取点,使,过点C作,垂足为H.
∵AB=10,BC=6,AC=8,
∴
∴是直角三角形,且
∴
∴,
∵,
∴当C、E、共线,且点与H重合时,的值最小,最小值为4.8,
故答案为:4.8.
21.
解:
为直角三角形,
在中
22.90°
解:在直角△BCD中,∠C=90°,BC=3,CD=4,
∴BD=5,
在△ABD中,AD2=132=169,AB2+BD2=122+52=144+25=169,
∴AD2=AB2+BD2,
∴△ABD是直角三角形,
∴∠ABD=90°.
23.(1)直角三角形,见解析
(2)cm
(1)
解:△ABC为直角三角形,理由如下:
∵,,,
∴,
∴△ABC为直角三角形.
(2)
解:折叠纸片点B与点A重合,DE为折痕,
∴,
设,则,
在Rt△ACE中由勾股定理得,,
解得:.
∴.
24.(1)AB=10
(2)24
(1)
解:∵△ABE的面积为35,DE=7,DE⊥AB,
∴AB×7=35,
解得:AB=10;
(2)
解:在△ABC中,AB2=102=100,AC2+BC2=62+82=100,
则AB2=AC2+BC2,
∴∠C=90°,
∴S△ABC=AC BC=×6×8=24,
答:△ACB的面积24.
25.(1)见解析
(2)海港C受台风影响,理由见解析
(3)3.5h
(1)
解:∵km,km,km,
∴.
∴是直角三角形,
∴;
(2)
解:海港C受台风影响.理由如下:
如图,过点C作于D.
∵,
∴.
∵,
∴海港C受到台风影响.
(3)
解:如图,在线段AB上取点E,F,使km,km,则台风中心在线段EF上时正好影响C港口.
∴EC=FC,
∵CD⊥AB,
∴ED=FD,
在中,由勾股定理得:
,
∴km,
∵台风的速度为40km/h,
∴.
∴台风影响该海港持续的时间为3.5h .
答案第1页,共2页
