2021-2022学年人教版八年级数学下册17.1勾股定理同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册17.1勾股定理同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 11:02:42 | ||
图片预览

文档简介
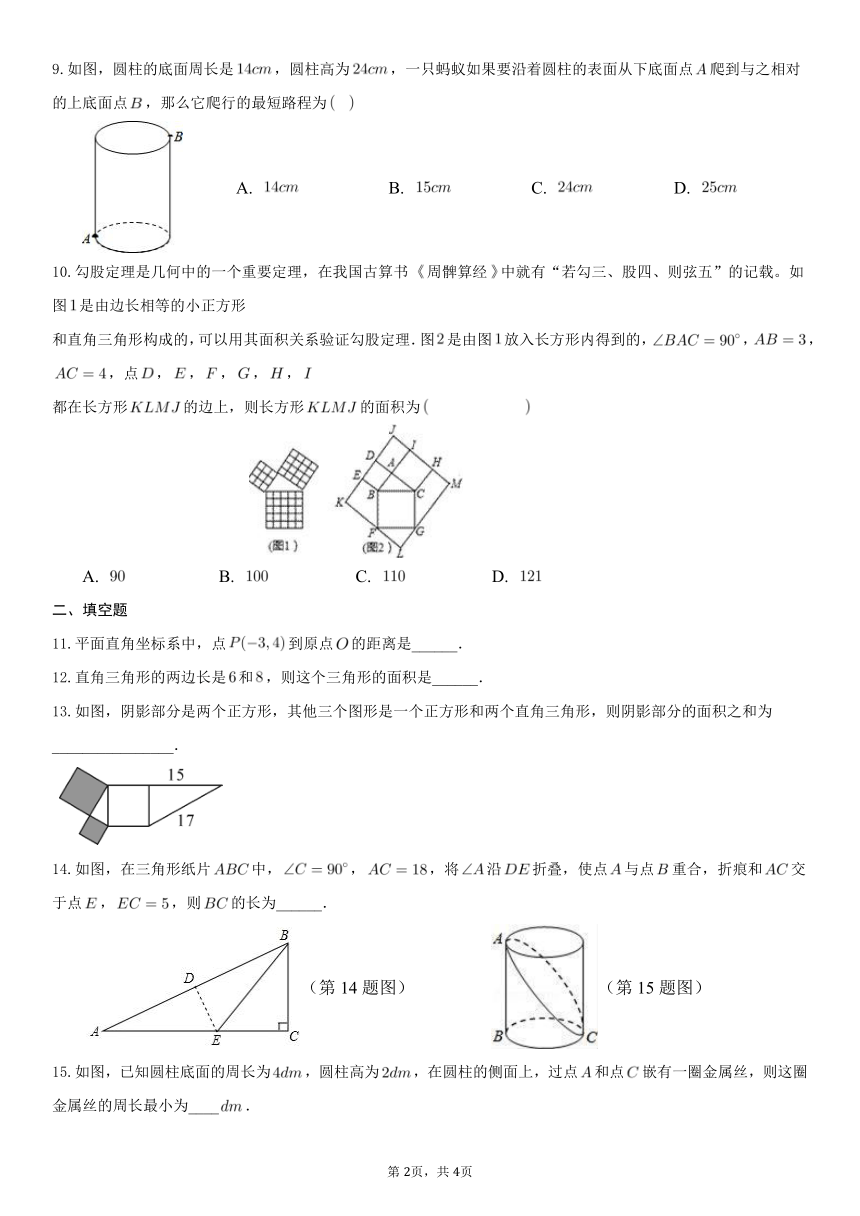
17.1 勾股定理 课时训练
一、单项选择题
1.在中,,,,则的长是
A. B. C. D.
2.我国汉代的赵爽在注释周髀算经时给出了勾股定理的无字证明,人们称它为“赵爽弦图”,“赵爽弦图”指的是
A. B. C. D.
3.下列说法中正确的是
A. 已知,,是三角形的三边,则
B. 在直角三角形中两边和的平方等于第三边的平方
C. 在中,,所以
D. 在中,,所以
4.直角三角形两边长分别为为和,则另一边长为
A. B. C. 或 D. 不确定
5.如图,两个较大正方形的面积分别为,,则字母所代表的正方形的面积为
A. B. C. D.
6.如下图进行尺规作图,则这点表示的实数是
A. B. C. D.
7.小明想知道学校旗杆垂直地面的高,他发现旗杆上的绳子垂到地面还多了,当他把绳子拉直后,发现绳子下端拉开,且下端刚好接触地面,则旗杆的高是
A. B. C. D.
8.如图,将边长分别是,的矩形纸片折叠,使点与点重合,则的长是
A. B. C. D.
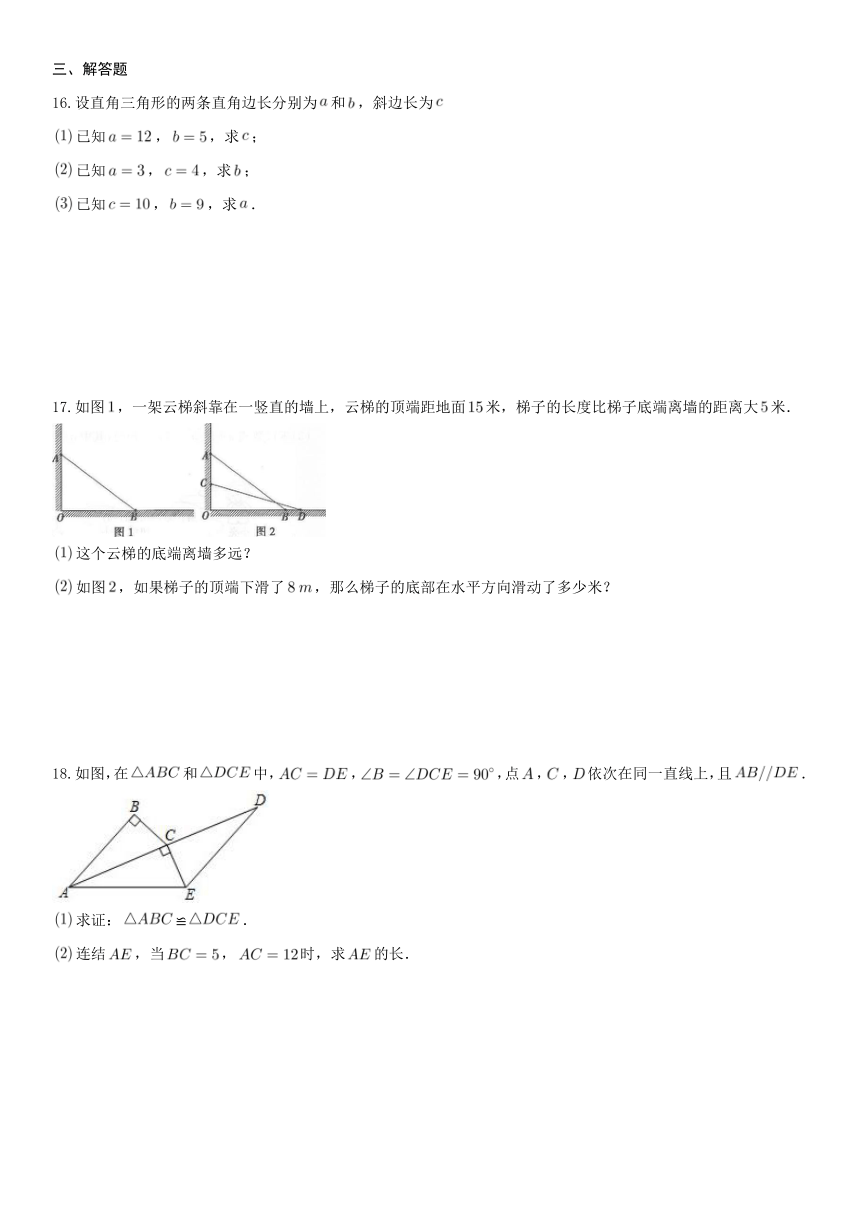
9.如图,圆柱的底面周长是,圆柱高为,一只蚂蚁如果要沿着圆柱的表面从下底面点爬到与之相对的上底面点,那么它爬行的最短路程为
A. B. C. D.
10.勾股定理是几何中的一个重要定理,在我国古算书周髀算经中就有“若勾三、股四、则弦五”的记载。如图是由边长相等的小正方形
和直角三角形构成的,可以用其面积关系验证勾股定理.图是由图放入长方形内得到的,,,,点,,,,,
都在长方形的边上,则长方形的面积为
A. B. C. D.
二、填空题
11.平面直角坐标系中,点到原点的距离是______.
12.直角三角形的两边长是和,则这个三角形的面积是______.
13.如图,阴影部分是两个正方形,其他三个图形是一个正方形和两个直角三角形,则阴影部分的面积之和为________________.
14.如图,在三角形纸片中,,,将沿折叠,使点与点重合,折痕和交于点,,则的长为______.
(第14题图) (第15题图)
15.如图,已知圆柱底面的周长为,圆柱高为,在圆柱的侧面上,过点和点嵌有一圈金属丝,则这圈金属丝的周长最小为____.
三、解答题
16.设直角三角形的两条直角边长分别为和,斜边长为
已知,,求;
已知,,求;
已知,,求.
17.如图,一架云梯斜靠在一竖直的墙上,云梯的顶端距地面米,梯子的长度比梯子底端离墙的距离大米.
这个云梯的底端离墙多远?
如图,如果梯子的顶端下滑了,那么梯子的底部在水平方向滑动了多少米?
18.如图,在和中,,,点,,依次在同一直线上,且.
求证:≌.
连结,当,时,求的长.
19.如图,一巡逻艇在处,发现一走私船在处的南偏东方向上距离处海里的处,并以每小时海里的速度沿南偏西方向行驶,若巡逻艇以每小时海里的速度追赶走私船,则追上走私船所需时间是多少?
20.如图,在长方形纸片中,,,点在上,将沿折叠,使点落在对角线上的点处,求的长.
第2页,共2页
答案和解析
1-10
11、
12、或
13、
14、
15、
16、解:直角三角形的两条直角边长分别为和,斜边长为,,,
;
直角三角形的两条直角边长分别为和,斜边长为,,,
;
直角三角形的两条直角边长分别为和,斜边长为,,,
.
17、解:根据题意可得米,米,
由勾股定理,可得:
解得:,
答:这个云梯的底端离墙米远;
由可得:米,
根据题意可得:米,米,
由勾股定理,可得:,
米,
答:梯子的底部在水平方向滑动了米.
18、证明:,,
又,,≌;
≌,,
,.
19、解:走私船在处的南偏东方向上,,
走私船在处沿南偏西方向行驶,,.
设追上走私船所需时间是小时,则
解得不合题意,舍去或.
答:追上走私船所需时间小时.
20、解:在长方纸片中,,,
,,
,
根据折叠可得,,,,
,
设,则,,
在中,,解得,
.
一、单项选择题
1.在中,,,,则的长是
A. B. C. D.
2.我国汉代的赵爽在注释周髀算经时给出了勾股定理的无字证明,人们称它为“赵爽弦图”,“赵爽弦图”指的是
A. B. C. D.
3.下列说法中正确的是
A. 已知,,是三角形的三边,则
B. 在直角三角形中两边和的平方等于第三边的平方
C. 在中,,所以
D. 在中,,所以
4.直角三角形两边长分别为为和,则另一边长为
A. B. C. 或 D. 不确定
5.如图,两个较大正方形的面积分别为,,则字母所代表的正方形的面积为
A. B. C. D.
6.如下图进行尺规作图,则这点表示的实数是
A. B. C. D.
7.小明想知道学校旗杆垂直地面的高,他发现旗杆上的绳子垂到地面还多了,当他把绳子拉直后,发现绳子下端拉开,且下端刚好接触地面,则旗杆的高是
A. B. C. D.
8.如图,将边长分别是,的矩形纸片折叠,使点与点重合,则的长是
A. B. C. D.
9.如图,圆柱的底面周长是,圆柱高为,一只蚂蚁如果要沿着圆柱的表面从下底面点爬到与之相对的上底面点,那么它爬行的最短路程为
A. B. C. D.
10.勾股定理是几何中的一个重要定理,在我国古算书周髀算经中就有“若勾三、股四、则弦五”的记载。如图是由边长相等的小正方形
和直角三角形构成的,可以用其面积关系验证勾股定理.图是由图放入长方形内得到的,,,,点,,,,,
都在长方形的边上,则长方形的面积为
A. B. C. D.
二、填空题
11.平面直角坐标系中,点到原点的距离是______.
12.直角三角形的两边长是和,则这个三角形的面积是______.
13.如图,阴影部分是两个正方形,其他三个图形是一个正方形和两个直角三角形,则阴影部分的面积之和为________________.
14.如图,在三角形纸片中,,,将沿折叠,使点与点重合,折痕和交于点,,则的长为______.
(第14题图) (第15题图)
15.如图,已知圆柱底面的周长为,圆柱高为,在圆柱的侧面上,过点和点嵌有一圈金属丝,则这圈金属丝的周长最小为____.
三、解答题
16.设直角三角形的两条直角边长分别为和,斜边长为
已知,,求;
已知,,求;
已知,,求.
17.如图,一架云梯斜靠在一竖直的墙上,云梯的顶端距地面米,梯子的长度比梯子底端离墙的距离大米.
这个云梯的底端离墙多远?
如图,如果梯子的顶端下滑了,那么梯子的底部在水平方向滑动了多少米?
18.如图,在和中,,,点,,依次在同一直线上,且.
求证:≌.
连结,当,时,求的长.
19.如图,一巡逻艇在处,发现一走私船在处的南偏东方向上距离处海里的处,并以每小时海里的速度沿南偏西方向行驶,若巡逻艇以每小时海里的速度追赶走私船,则追上走私船所需时间是多少?
20.如图,在长方形纸片中,,,点在上,将沿折叠,使点落在对角线上的点处,求的长.
第2页,共2页
答案和解析
1-10
11、
12、或
13、
14、
15、
16、解:直角三角形的两条直角边长分别为和,斜边长为,,,
;
直角三角形的两条直角边长分别为和,斜边长为,,,
;
直角三角形的两条直角边长分别为和,斜边长为,,,
.
17、解:根据题意可得米,米,
由勾股定理,可得:
解得:,
答:这个云梯的底端离墙米远;
由可得:米,
根据题意可得:米,米,
由勾股定理,可得:,
米,
答:梯子的底部在水平方向滑动了米.
18、证明:,,
又,,≌;
≌,,
,.
19、解:走私船在处的南偏东方向上,,
走私船在处沿南偏西方向行驶,,.
设追上走私船所需时间是小时,则
解得不合题意,舍去或.
答:追上走私船所需时间小时.
20、解:在长方纸片中,,,
,,
,
根据折叠可得,,,,
,
设,则,,
在中,,解得,
.
