2021-2022学年苏科版数学七年级下册第8章幂的运算计算力提升训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学七年级下册第8章幂的运算计算力提升训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 11:05:34 | ||
图片预览

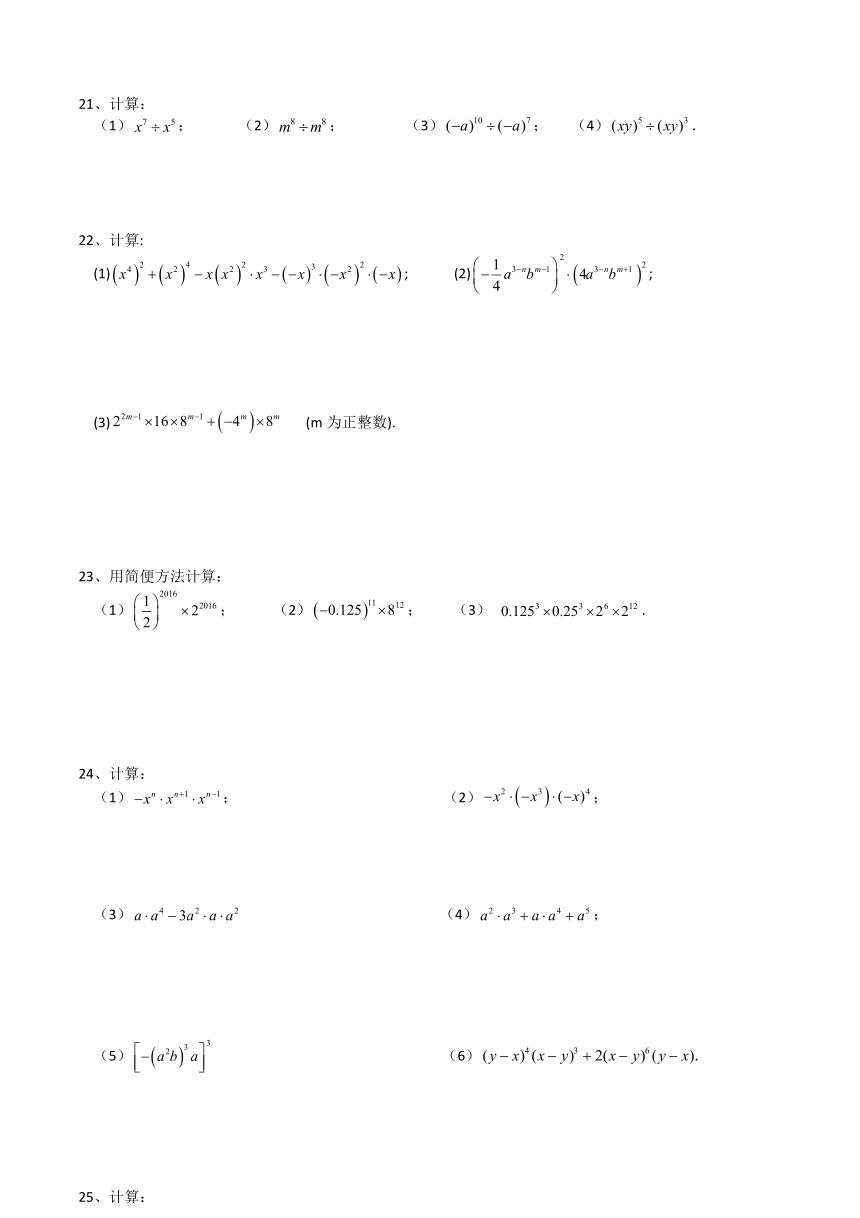



文档简介
第8章 8.1~8.3.1计算力提升训练
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、(2021·通道侗族自治县教育科学研究室七年级期中)计算的结果是( )
A. B. C. D.
2、(2021·河北滦南·)y2m2可以改写成( )
A.ym+y2 B.(ym)2 C.ym y2 D.2ym
3、(2021·上海·初一期末)下列运算正确的是( )
A. B. C. D.
4、(2021·长沙市开福区青竹湖湘一外国语学校)下列计算正确的是( )
A. B. C. D.
5、计算的结果是( )
A. B. C. D.
6、(2021·浙江金华市·七年级期中)若,,则等于( )
A.9 B.18 C.11 D.14
7、(2020·山东中区·初一期末)已知则的大小关系是( )
A. B. C. D.
8、(2021·山东寒亭·七年级期中)若,,,则( )
A. B. C. D.
9、(2021·浙江八年级期末)我们知道下面的结论:若(,且),则.利用这个结论解决下列问题:设.现给出三者之间的三个关系式:①,
②,③.其中正确的是( )
A.①② B.①③ C.②③ D.①
10、(2021·江苏句容·七年级期中)规定,例如:;若,则x的值为( )
A.29 B.4 C.3 D.2
二、填空题
11、(2021·山东日照·)在等式中,括号内的代数式为______.
12、(2021·余姚市兰江中学七年级期中)若,则________.
13、已知,则=__________.
14、已知,则=_______.
15、(2021·江西南城·七年级期中)若,则_______.
16、(2021·重庆八中初一期中)已知,则的值是______.
17、已知a=255,b=344,c=433,则a,b,c的大小关系为______.
18、(2021·南靖县城关中学)已知,则m的值是_________________.
三、解答题
19、计算
(1)a a2 a3; (2)(﹣2ab)2;
(3)(a3)5; (4)(﹣a)6÷(﹣a)2÷(﹣a)2.
20、计算:(1); (2); (3).
21、计算:
(1); (2); (3); (4).
22、计算:
(1); (2);
(3) (m为正整数).
23、用简便方法计算:
(1); (2); (3) .
24、计算:
(1); (2);
(3) (4);
(5) (6).
25、计算:
(1); (2); (3);
(4); (5).
26、(1)若,,求的值; (2)计算的值.
27、(1)已知,,求:①的值; ②的值;
(2)已知,求的值
28、已知:,,.
(1)求的值.
(2)求的值.
(3)直接写出字母、、之间的数量关系.
29、(1)若,,求的值;
(2)若,求的值;
(3)比较大小:,,.
30、(2020·江苏苏州·七年级期中)(1)已知,求x的值,
(2)若,,求.
31、(1)若,求的值;
(2)已知,,求的值.
32、小明和小红在计算时,分别采用了不同的解法.
小明的解法:,
小红的解法:.
请你借鉴小明和小红的解题思路,解决下列问题:
(1)若,求的值;
(2)已知满足,求的值
33、(2021·河南八年级月考)规定,求:
(1)求; (2)若,求x的值.
34、(2021·福建南靖·八年级期中)阅读:已知正整数a、b、c,显然,当同底数时,指数大的幂也大,若对于同指数,不同底数的两个幂和,当时,则有,根据上述材料,回答下列问题.
(1)比较大小:__________(填写>、<或=).
(2)比较与的大小(写出比较的具体过程).
(3)计算.
第8章 8.1~8.3.1计算力提升训练
-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、(2021·通道侗族自治县教育科学研究室七年级期中)计算的结果是( )
A. B. C. D.
【答案】B
【分析】根据积的乘方的运算法则求解即可.
【详解】解:故答案为:B
2、(2021·河北滦南·)y2m2可以改写成( )
A.ym+y2 B.(ym)2 C.ym y2 D.2ym
【答案】B
【分析】根据积的乘方法则的逆运用,即可得到答案.
【详解】解:y2m2=(ym)2,故选B.
3、(2021·上海·初一期末)下列运算正确的是( )
A. B. C. D.
【答案】D
【分析】利用幂的乘方、积的乘方、同底数幂的乘法以及同底数幂的除法的性质求解即可求得答案.注意掌握排除法在选择题中的应用.
【解析】解:A.(a2)3=a6,故本选项错误; B.,故本选项错误;
C.a6÷a3=a3,故本选项错误;D.a2 a3=a5,故本选项正确.故选D.
4、(2021·长沙市开福区青竹湖湘一外国语学校)下列计算正确的是( )
A. B. C. D.
【答案】D
【分析】分别根据同底数幂的乘法法则,积的乘方运算法则,以及幂的乘方法则逐一判断即可.
【详解】解:A.,故本选项不符合题意;B.,故本选项不合题意;
C.,故本选项不合题意;D.,故本选项符合题意;故选:D.
5、计算的结果是( )
A. B. C. D.
【答案】A
【分析】将化为使两个幂的指数相同,再利用积的乘方逆运算进行计算.
解:,
故选:A.
6、(2021·浙江金华市·七年级期中)若,,则等于( )
A.9 B.18 C.11 D.14
【答案】A
【分析】根据同底数幂的除法法则将转化为,即可求解.
【详解】解:∵,,∴.故选:A.
7、(2020·山东中区·初一期末)已知则的大小关系是( )
A. B. C. D.
【答案】A
【分析】先把a,b,c化成以3为底数的幂的形式,再比较大小.
【解析】解:故选A.
8、(2021·山东寒亭·七年级期中)若,,,则( )
A. B. C. D.
【答案】A
【分析】直接利用同底数幂的乘法运算法则以及幂的乘方运算法则将所给出的条件式进行变形得出答案.
【详解】解:∵,,,∴,,,
∵ ,即∴故选:A
9、(2021·浙江八年级期末)我们知道下面的结论:若(,且),则.利用这个结论解决下列问题:设.现给出三者之间的三个关系式:①,
②,③.其中正确的是( )
A.①② B.①③ C.②③ D.①
【答案】B
【分析】根据同底数幂的乘除法公式即可求出m、n、p的关系.
【详解】解:∵,∴n=1+m,m=n-1,
∵,∴p=1+n=1+1+m=2+m,
①m+p=n-1+1+n=2n,故正确;②3m+n=3(p-2)+p-1=4p-7,故错误;
③===3,故正确;故选B.
10、(2021·江苏句容·七年级期中)规定,例如:;若,则x的值为( )
A.29 B.4 C.3 D.2
【答案】D
【分析】根据定义新运算列出相应的等式,然后利用同底数幂的乘法法则进行计算求解.
【详解】解:∵,由题意可得:
∴∴,解得故选:D.
二、填空题
11、(2021·山东日照·)在等式中,括号内的代数式为______.
【答案】
【分析】根据同底数幂乘法的计算法则,得出答案.
【详解】解:,故答案为:.
12、(2021·余姚市兰江中学七年级期中)若,则________.
【答案】3
【分析】根据同底数幂相除,底数不变,指数相减即可即可求解.
【详解】∵,∴,∴,故答案为:3.
13、已知,则=__________.
【分析】根据积的乘方和幂的乘方的逆运算,把等式变形,根据指数相同求解即可.
解:,
根据积的乘方和幂的乘方,等式可变形为:,
即,
,
解得,
故答案为:8.
14、已知,则=_______.
【分析】根据题意可得2x-3y=2,然后根据幂的乘方和同底数幂相除,底数不变,指数相减即可求得答案.
解:由已知可得2x-3y=2,
所以=102x÷103y=102x-3y=102=100.
故答案为100.
15、(2021·江西南城·七年级期中)若,则_______.
【答案】3
【分析】根据同底数幂的乘法法则,即可求解.
【详解】解:∵,∴,又∵,∴12÷4=3,故答案是:3.
16、(2021·重庆八中初一期中)已知,则的值是______.
【答案】16
【分析】根据题意利用同底数幂的除法以及幂的乘方的运算法则进行变形与代入运算即可.
【解析】解:∵,,
∴,∴.故答案为:16.
17、已知a=255,b=344,c=433,则a,b,c的大小关系为______.
【分析】根据幂运算的性质,及它们的指数相同,只需比较它们的底数的大小,底数大的就大.
解:a=255=(25)11=3211,
b=344=(34)11=8111,
c=433=(43)11=6411,
则b>c>a.
18、(2021·南靖县城关中学)已知,则m的值是_________________.
【答案】2
【分析】根据同底数幂的乘法法则将原式变形可得,再利用乘法分配律合并计算,得到m值.
【详解】解:∵,∴,
∴,∴,∴m=2,故答案为:2.
三、解答题
19、计算
(1)a a2 a3; (2)(﹣2ab)2;
(3)(a3)5; (4)(﹣a)6÷(﹣a)2÷(﹣a)2.
【答案】(1)a6;(2)4a2b2;(3)a15;(4)a2
【解析】
【分析】(1)根据同底数幂的乘法法则,即可求解;
(2)根据幂的乘方法则,即可求解;
(3)根据幂的乘方法则,即可求解;
(4)先算乘方,再根据同底数幂的除法法则,即可求解.
解:(1)原式=a1+2+3= a6;
(2)原式=4a2b2;
(3)原式=a15;
(4)原式=a6÷a2÷a2= a2.
20、计算:(1); (2); (3).
【答案】(1);(2);(3)
【分析】本题考查幂的乘方法则,运用幂的乘方法则进行计算时要注意符号的计算及处理,一定不要将幂的乘方与同底数幂的乘法混淆.幂的乘方法则中的底数仍可以为单个数字、字母,也可以是单项式或多项式.熟练掌握幂的乘方法则是解题关键.(1)题中的底数是,(2)题中的底数是,(3)题中的底数的指数是,乘方以后的指数应是.
解:(1).
(2).
(3).
21、计算:
(1); (2); (3); (4).
【答案】(1);(2)1;(3);(4)
【分析】本题考查同底数幂的除法和积的乘方法则.同底数幂的除法法则:底数不变,指数相减.积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘.
(1)根据同底数幂的除法法则计算即可;
(2)根据同底数幂的除法法则计算即可;
(3)根据同底数幂的除法法则计算即可;
(4)根据同底数幂的除法法则和积的乘方法则计算即可.
解:(1)原式==;
(2)原式===1;
(3)原式===;
(4)原式===.
22、计算:
(1); (2);
(3) (m为正整数).
【答案】(1)0;(2);(3)0.
试题分析:(1)先进行幂的乘方运算,再进行幂的乘法运算,最后进行加减运算;(2)先进行积的乘方运算,再进行幂的乘法运算;(3)先将式子变形为底数相同的形式,然后再计算幂的乘方,幂的乘法,最后进行减法运算.
试题解析:
(1)原式=x8+x8-x·x4·x3+x3·x4×(-x)= x8+x8-x8-x8=0;
(2)原式=(a6-2nb2m-2)(16a6-2nb2m+2)=a12-4nb4m;
(3)原式=22m-1×24×(23)m-1+(-22m)×23m=22m+3×23m-3-25m=25m-25m=0.
23、用简便方法计算:
(1); (2); (3) .
【答案】(1)1;(2)-8;(3)8
【分析】(1)此题逆用积的乘方,即进行计算;(2)先将812写成,再将与相乘,最后化简结果即可;(3)将26写成43,将212写成84,再将43与0.253相乘,将84与0.1253相乘,再将乘积相乘即可得到答案.
解:(1)=1;
(2)=-8;
(3)=8.
24、计算:
(1); (2);
(3) (4);
(5) (6).
【答案】(1);(2);(3);(4);(5);(6).
【分析】(1)根据同底数幂相乘法则计算;
(2)根据乘法法则及同底数幂相乘法则计算;
(3)根据同底数幂相乘法则及合并同类项法则计算;
(4)根据同底数幂乘法法则及合并同类项法则计算;
(5)根据幂的乘方及积的乘方法则计算;
(6)先将多项式变为同底数的形式,再根据同底数幂乘法法则及合并同类项法则计算.
解:(1)=;
(2)==;
(3)==;
(4)==;
(5)= =;
(6)===.
25、计算:
(1); (2); (3);
(4); (5).
【答案】(1);(2);(3);(4);(5).
【分析】(1)先计算同底数幂的除法,然后计算积的乘方即可;
(2)利用同底数幂的除法计算法则求解即可;
(3)先得到,然后利用同底数幂的除法计算法则求解即可;
(4)先计算同底数幂的除法,然后计算积的乘方即可;
(5)直接根据同底数幂的乘除法计算法则求解即可.
解:(1);
(2);
(3);
(4);
(5).
26、(1)若,,求的值; (2)计算的值.
【答案】(1);(2).
【分析】(1)逆用同底数幂的除法的运算法则解答即可;(2)设S=,则2S=, 把这两个式子相减即可求解.
解:(1)∵,,
∴;
(2) 设S=,
则2S=,
∴S=2S-S=.
27、(1)已知,,求:①的值; ②的值;
(2)已知,求的值
【答案】(1)①6;②;(2)6
解:试题分析:(1)根据同底数幂的乘法法则和除法法则求解即可;
(2)把各个数字化为以2为底数的形式,按照同底数幂的乘法法则,求解即可.
试题解析:
(1),
.
(2)因为,所以,即:,故,
所以.
28、已知:,,.
(1)求的值.
(2)求的值.
(3)直接写出字母、、之间的数量关系.
【答案】(1);(2);(3)
【分析】(1)直接将代入计算即可;
(2)逆运用同底数幂乘法和除法公式变形后代入计算即可;
(3)结合(1)中,再观察,,易得9×8=72,利用幂的乘方和同底数幂乘法变形即可得出.
解:解(1)∵,
∴;
(2)∵,,,
∴;
(3)∵,
∴,即.
29、(1)若,,求的值;
(2)若,求的值;
(3)比较大小:,,.
【答案】(1)108;(2)8;(3).
【分析】(1)根据求解即可;
(2)根据求解即可;
(3)先得到,,,然后比较大小即可.
解:(1)∵,,
∴;
(2)∵,
∴;
(3),,
∵,
∴.
30、(2020·江苏苏州·七年级期中)(1)已知,求x的值,
(2)若,,求.
【答案】(1);(2)
【分析】(1)根据幂的乘方的逆用可直接进行求解;
(2)根据积的乘方和幂的乘方的逆用可直接进行求解.
【详解】解:(1)∵,∴,∴,解得:;
(2)∵,,∴.
31、(1)若,求的值;
(2)已知,,求的值.
【答案】(1)27;(2)27
【分析】(1)把27x 9y都改为底数为3的乘方,再利用同底数幂的乘法计算,由3x+2y-3=0得出3x+2y=3整体代入即可.
(2)先根据幂的乘方的法则分别求出32m和34n的值,然后根据同底数幂的乘除法法则求解.
解:(1)∵3x+2y-3=0,
∴3x+2y=3
∴27x 9y=33x 32y=33x+2y,=33=27.
(2)∵3m=6,9n=2,
∴32m=(3m)2=36,34n=(32n)2=(9n)2=4,
∴==.
32、小明和小红在计算时,分别采用了不同的解法.
小明的解法:,
小红的解法:.
请你借鉴小明和小红的解题思路,解决下列问题:
(1)若,求的值;
(2)已知满足,求的值
【答案】(1)27;(2).
【分析】本题考查了同底数幂的运算,熟悉相关性质是解题的关键.
(1)根据同底数幂的乘法和除法化简,然后再计算即可;
(2)将化成,然后得到,然后再化成指数相同计算即可.
解:(1)
∵∴
∴原式;
(2)∵
∴
∴
∴
∴
∴
∴
∴.
33、(2021·河南八年级月考)规定,求:
(1)求; (2)若,求x的值.
【答案】(1);(2)
【分析】(1)根据规定即可完成;(2)根据规定及幂的运算,可得关于x的方程,解方程即可.
【详解】(1),;
(2),,则,解得:.
34、(2021·福建南靖·八年级期中)阅读:已知正整数a、b、c,显然,当同底数时,指数大的幂也大,若对于同指数,不同底数的两个幂和,当时,则有,根据上述材料,回答下列问题.
(1)比较大小:__________(填写>、<或=).
(2)比较与的大小(写出比较的具体过程).
(3)计算.
【答案】(1)>;(2)<;(3)-4
【分析】(1)根据同指数的幂底数越大幂越大,可得答案;
(2)根据幂的乘方,可得指数相同的幂,根据底数越大幂越大,可得答案;
(3)先根据积的乘方逆运算进行运算,再进行减法运算即可得出答案.
【详解】解:(1)∵5>4,∴>,故答案为:>;
(2)∵233=(23)11=811,322=(32)11=911,又∵8<9, ∴<.
(3)
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、(2021·通道侗族自治县教育科学研究室七年级期中)计算的结果是( )
A. B. C. D.
2、(2021·河北滦南·)y2m2可以改写成( )
A.ym+y2 B.(ym)2 C.ym y2 D.2ym
3、(2021·上海·初一期末)下列运算正确的是( )
A. B. C. D.
4、(2021·长沙市开福区青竹湖湘一外国语学校)下列计算正确的是( )
A. B. C. D.
5、计算的结果是( )
A. B. C. D.
6、(2021·浙江金华市·七年级期中)若,,则等于( )
A.9 B.18 C.11 D.14
7、(2020·山东中区·初一期末)已知则的大小关系是( )
A. B. C. D.
8、(2021·山东寒亭·七年级期中)若,,,则( )
A. B. C. D.
9、(2021·浙江八年级期末)我们知道下面的结论:若(,且),则.利用这个结论解决下列问题:设.现给出三者之间的三个关系式:①,
②,③.其中正确的是( )
A.①② B.①③ C.②③ D.①
10、(2021·江苏句容·七年级期中)规定,例如:;若,则x的值为( )
A.29 B.4 C.3 D.2
二、填空题
11、(2021·山东日照·)在等式中,括号内的代数式为______.
12、(2021·余姚市兰江中学七年级期中)若,则________.
13、已知,则=__________.
14、已知,则=_______.
15、(2021·江西南城·七年级期中)若,则_______.
16、(2021·重庆八中初一期中)已知,则的值是______.
17、已知a=255,b=344,c=433,则a,b,c的大小关系为______.
18、(2021·南靖县城关中学)已知,则m的值是_________________.
三、解答题
19、计算
(1)a a2 a3; (2)(﹣2ab)2;
(3)(a3)5; (4)(﹣a)6÷(﹣a)2÷(﹣a)2.
20、计算:(1); (2); (3).
21、计算:
(1); (2); (3); (4).
22、计算:
(1); (2);
(3) (m为正整数).
23、用简便方法计算:
(1); (2); (3) .
24、计算:
(1); (2);
(3) (4);
(5) (6).
25、计算:
(1); (2); (3);
(4); (5).
26、(1)若,,求的值; (2)计算的值.
27、(1)已知,,求:①的值; ②的值;
(2)已知,求的值
28、已知:,,.
(1)求的值.
(2)求的值.
(3)直接写出字母、、之间的数量关系.
29、(1)若,,求的值;
(2)若,求的值;
(3)比较大小:,,.
30、(2020·江苏苏州·七年级期中)(1)已知,求x的值,
(2)若,,求.
31、(1)若,求的值;
(2)已知,,求的值.
32、小明和小红在计算时,分别采用了不同的解法.
小明的解法:,
小红的解法:.
请你借鉴小明和小红的解题思路,解决下列问题:
(1)若,求的值;
(2)已知满足,求的值
33、(2021·河南八年级月考)规定,求:
(1)求; (2)若,求x的值.
34、(2021·福建南靖·八年级期中)阅读:已知正整数a、b、c,显然,当同底数时,指数大的幂也大,若对于同指数,不同底数的两个幂和,当时,则有,根据上述材料,回答下列问题.
(1)比较大小:__________(填写>、<或=).
(2)比较与的大小(写出比较的具体过程).
(3)计算.
第8章 8.1~8.3.1计算力提升训练
-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、(2021·通道侗族自治县教育科学研究室七年级期中)计算的结果是( )
A. B. C. D.
【答案】B
【分析】根据积的乘方的运算法则求解即可.
【详解】解:故答案为:B
2、(2021·河北滦南·)y2m2可以改写成( )
A.ym+y2 B.(ym)2 C.ym y2 D.2ym
【答案】B
【分析】根据积的乘方法则的逆运用,即可得到答案.
【详解】解:y2m2=(ym)2,故选B.
3、(2021·上海·初一期末)下列运算正确的是( )
A. B. C. D.
【答案】D
【分析】利用幂的乘方、积的乘方、同底数幂的乘法以及同底数幂的除法的性质求解即可求得答案.注意掌握排除法在选择题中的应用.
【解析】解:A.(a2)3=a6,故本选项错误; B.,故本选项错误;
C.a6÷a3=a3,故本选项错误;D.a2 a3=a5,故本选项正确.故选D.
4、(2021·长沙市开福区青竹湖湘一外国语学校)下列计算正确的是( )
A. B. C. D.
【答案】D
【分析】分别根据同底数幂的乘法法则,积的乘方运算法则,以及幂的乘方法则逐一判断即可.
【详解】解:A.,故本选项不符合题意;B.,故本选项不合题意;
C.,故本选项不合题意;D.,故本选项符合题意;故选:D.
5、计算的结果是( )
A. B. C. D.
【答案】A
【分析】将化为使两个幂的指数相同,再利用积的乘方逆运算进行计算.
解:,
故选:A.
6、(2021·浙江金华市·七年级期中)若,,则等于( )
A.9 B.18 C.11 D.14
【答案】A
【分析】根据同底数幂的除法法则将转化为,即可求解.
【详解】解:∵,,∴.故选:A.
7、(2020·山东中区·初一期末)已知则的大小关系是( )
A. B. C. D.
【答案】A
【分析】先把a,b,c化成以3为底数的幂的形式,再比较大小.
【解析】解:故选A.
8、(2021·山东寒亭·七年级期中)若,,,则( )
A. B. C. D.
【答案】A
【分析】直接利用同底数幂的乘法运算法则以及幂的乘方运算法则将所给出的条件式进行变形得出答案.
【详解】解:∵,,,∴,,,
∵ ,即∴故选:A
9、(2021·浙江八年级期末)我们知道下面的结论:若(,且),则.利用这个结论解决下列问题:设.现给出三者之间的三个关系式:①,
②,③.其中正确的是( )
A.①② B.①③ C.②③ D.①
【答案】B
【分析】根据同底数幂的乘除法公式即可求出m、n、p的关系.
【详解】解:∵,∴n=1+m,m=n-1,
∵,∴p=1+n=1+1+m=2+m,
①m+p=n-1+1+n=2n,故正确;②3m+n=3(p-2)+p-1=4p-7,故错误;
③===3,故正确;故选B.
10、(2021·江苏句容·七年级期中)规定,例如:;若,则x的值为( )
A.29 B.4 C.3 D.2
【答案】D
【分析】根据定义新运算列出相应的等式,然后利用同底数幂的乘法法则进行计算求解.
【详解】解:∵,由题意可得:
∴∴,解得故选:D.
二、填空题
11、(2021·山东日照·)在等式中,括号内的代数式为______.
【答案】
【分析】根据同底数幂乘法的计算法则,得出答案.
【详解】解:,故答案为:.
12、(2021·余姚市兰江中学七年级期中)若,则________.
【答案】3
【分析】根据同底数幂相除,底数不变,指数相减即可即可求解.
【详解】∵,∴,∴,故答案为:3.
13、已知,则=__________.
【分析】根据积的乘方和幂的乘方的逆运算,把等式变形,根据指数相同求解即可.
解:,
根据积的乘方和幂的乘方,等式可变形为:,
即,
,
解得,
故答案为:8.
14、已知,则=_______.
【分析】根据题意可得2x-3y=2,然后根据幂的乘方和同底数幂相除,底数不变,指数相减即可求得答案.
解:由已知可得2x-3y=2,
所以=102x÷103y=102x-3y=102=100.
故答案为100.
15、(2021·江西南城·七年级期中)若,则_______.
【答案】3
【分析】根据同底数幂的乘法法则,即可求解.
【详解】解:∵,∴,又∵,∴12÷4=3,故答案是:3.
16、(2021·重庆八中初一期中)已知,则的值是______.
【答案】16
【分析】根据题意利用同底数幂的除法以及幂的乘方的运算法则进行变形与代入运算即可.
【解析】解:∵,,
∴,∴.故答案为:16.
17、已知a=255,b=344,c=433,则a,b,c的大小关系为______.
【分析】根据幂运算的性质,及它们的指数相同,只需比较它们的底数的大小,底数大的就大.
解:a=255=(25)11=3211,
b=344=(34)11=8111,
c=433=(43)11=6411,
则b>c>a.
18、(2021·南靖县城关中学)已知,则m的值是_________________.
【答案】2
【分析】根据同底数幂的乘法法则将原式变形可得,再利用乘法分配律合并计算,得到m值.
【详解】解:∵,∴,
∴,∴,∴m=2,故答案为:2.
三、解答题
19、计算
(1)a a2 a3; (2)(﹣2ab)2;
(3)(a3)5; (4)(﹣a)6÷(﹣a)2÷(﹣a)2.
【答案】(1)a6;(2)4a2b2;(3)a15;(4)a2
【解析】
【分析】(1)根据同底数幂的乘法法则,即可求解;
(2)根据幂的乘方法则,即可求解;
(3)根据幂的乘方法则,即可求解;
(4)先算乘方,再根据同底数幂的除法法则,即可求解.
解:(1)原式=a1+2+3= a6;
(2)原式=4a2b2;
(3)原式=a15;
(4)原式=a6÷a2÷a2= a2.
20、计算:(1); (2); (3).
【答案】(1);(2);(3)
【分析】本题考查幂的乘方法则,运用幂的乘方法则进行计算时要注意符号的计算及处理,一定不要将幂的乘方与同底数幂的乘法混淆.幂的乘方法则中的底数仍可以为单个数字、字母,也可以是单项式或多项式.熟练掌握幂的乘方法则是解题关键.(1)题中的底数是,(2)题中的底数是,(3)题中的底数的指数是,乘方以后的指数应是.
解:(1).
(2).
(3).
21、计算:
(1); (2); (3); (4).
【答案】(1);(2)1;(3);(4)
【分析】本题考查同底数幂的除法和积的乘方法则.同底数幂的除法法则:底数不变,指数相减.积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘.
(1)根据同底数幂的除法法则计算即可;
(2)根据同底数幂的除法法则计算即可;
(3)根据同底数幂的除法法则计算即可;
(4)根据同底数幂的除法法则和积的乘方法则计算即可.
解:(1)原式==;
(2)原式===1;
(3)原式===;
(4)原式===.
22、计算:
(1); (2);
(3) (m为正整数).
【答案】(1)0;(2);(3)0.
试题分析:(1)先进行幂的乘方运算,再进行幂的乘法运算,最后进行加减运算;(2)先进行积的乘方运算,再进行幂的乘法运算;(3)先将式子变形为底数相同的形式,然后再计算幂的乘方,幂的乘法,最后进行减法运算.
试题解析:
(1)原式=x8+x8-x·x4·x3+x3·x4×(-x)= x8+x8-x8-x8=0;
(2)原式=(a6-2nb2m-2)(16a6-2nb2m+2)=a12-4nb4m;
(3)原式=22m-1×24×(23)m-1+(-22m)×23m=22m+3×23m-3-25m=25m-25m=0.
23、用简便方法计算:
(1); (2); (3) .
【答案】(1)1;(2)-8;(3)8
【分析】(1)此题逆用积的乘方,即进行计算;(2)先将812写成,再将与相乘,最后化简结果即可;(3)将26写成43,将212写成84,再将43与0.253相乘,将84与0.1253相乘,再将乘积相乘即可得到答案.
解:(1)=1;
(2)=-8;
(3)=8.
24、计算:
(1); (2);
(3) (4);
(5) (6).
【答案】(1);(2);(3);(4);(5);(6).
【分析】(1)根据同底数幂相乘法则计算;
(2)根据乘法法则及同底数幂相乘法则计算;
(3)根据同底数幂相乘法则及合并同类项法则计算;
(4)根据同底数幂乘法法则及合并同类项法则计算;
(5)根据幂的乘方及积的乘方法则计算;
(6)先将多项式变为同底数的形式,再根据同底数幂乘法法则及合并同类项法则计算.
解:(1)=;
(2)==;
(3)==;
(4)==;
(5)= =;
(6)===.
25、计算:
(1); (2); (3);
(4); (5).
【答案】(1);(2);(3);(4);(5).
【分析】(1)先计算同底数幂的除法,然后计算积的乘方即可;
(2)利用同底数幂的除法计算法则求解即可;
(3)先得到,然后利用同底数幂的除法计算法则求解即可;
(4)先计算同底数幂的除法,然后计算积的乘方即可;
(5)直接根据同底数幂的乘除法计算法则求解即可.
解:(1);
(2);
(3);
(4);
(5).
26、(1)若,,求的值; (2)计算的值.
【答案】(1);(2).
【分析】(1)逆用同底数幂的除法的运算法则解答即可;(2)设S=,则2S=, 把这两个式子相减即可求解.
解:(1)∵,,
∴;
(2) 设S=,
则2S=,
∴S=2S-S=.
27、(1)已知,,求:①的值; ②的值;
(2)已知,求的值
【答案】(1)①6;②;(2)6
解:试题分析:(1)根据同底数幂的乘法法则和除法法则求解即可;
(2)把各个数字化为以2为底数的形式,按照同底数幂的乘法法则,求解即可.
试题解析:
(1),
.
(2)因为,所以,即:,故,
所以.
28、已知:,,.
(1)求的值.
(2)求的值.
(3)直接写出字母、、之间的数量关系.
【答案】(1);(2);(3)
【分析】(1)直接将代入计算即可;
(2)逆运用同底数幂乘法和除法公式变形后代入计算即可;
(3)结合(1)中,再观察,,易得9×8=72,利用幂的乘方和同底数幂乘法变形即可得出.
解:解(1)∵,
∴;
(2)∵,,,
∴;
(3)∵,
∴,即.
29、(1)若,,求的值;
(2)若,求的值;
(3)比较大小:,,.
【答案】(1)108;(2)8;(3).
【分析】(1)根据求解即可;
(2)根据求解即可;
(3)先得到,,,然后比较大小即可.
解:(1)∵,,
∴;
(2)∵,
∴;
(3),,
∵,
∴.
30、(2020·江苏苏州·七年级期中)(1)已知,求x的值,
(2)若,,求.
【答案】(1);(2)
【分析】(1)根据幂的乘方的逆用可直接进行求解;
(2)根据积的乘方和幂的乘方的逆用可直接进行求解.
【详解】解:(1)∵,∴,∴,解得:;
(2)∵,,∴.
31、(1)若,求的值;
(2)已知,,求的值.
【答案】(1)27;(2)27
【分析】(1)把27x 9y都改为底数为3的乘方,再利用同底数幂的乘法计算,由3x+2y-3=0得出3x+2y=3整体代入即可.
(2)先根据幂的乘方的法则分别求出32m和34n的值,然后根据同底数幂的乘除法法则求解.
解:(1)∵3x+2y-3=0,
∴3x+2y=3
∴27x 9y=33x 32y=33x+2y,=33=27.
(2)∵3m=6,9n=2,
∴32m=(3m)2=36,34n=(32n)2=(9n)2=4,
∴==.
32、小明和小红在计算时,分别采用了不同的解法.
小明的解法:,
小红的解法:.
请你借鉴小明和小红的解题思路,解决下列问题:
(1)若,求的值;
(2)已知满足,求的值
【答案】(1)27;(2).
【分析】本题考查了同底数幂的运算,熟悉相关性质是解题的关键.
(1)根据同底数幂的乘法和除法化简,然后再计算即可;
(2)将化成,然后得到,然后再化成指数相同计算即可.
解:(1)
∵∴
∴原式;
(2)∵
∴
∴
∴
∴
∴
∴
∴.
33、(2021·河南八年级月考)规定,求:
(1)求; (2)若,求x的值.
【答案】(1);(2)
【分析】(1)根据规定即可完成;(2)根据规定及幂的运算,可得关于x的方程,解方程即可.
【详解】(1),;
(2),,则,解得:.
34、(2021·福建南靖·八年级期中)阅读:已知正整数a、b、c,显然,当同底数时,指数大的幂也大,若对于同指数,不同底数的两个幂和,当时,则有,根据上述材料,回答下列问题.
(1)比较大小:__________(填写>、<或=).
(2)比较与的大小(写出比较的具体过程).
(3)计算.
【答案】(1)>;(2)<;(3)-4
【分析】(1)根据同指数的幂底数越大幂越大,可得答案;
(2)根据幂的乘方,可得指数相同的幂,根据底数越大幂越大,可得答案;
(3)先根据积的乘方逆运算进行运算,再进行减法运算即可得出答案.
【详解】解:(1)∵5>4,∴>,故答案为:>;
(2)∵233=(23)11=811,322=(32)11=911,又∵8<9, ∴<.
(3)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
