苏科版七年级数学下册 11.6 一元一次不等式(组)复习课 教案
文档属性
| 名称 | 苏科版七年级数学下册 11.6 一元一次不等式(组)复习课 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 67.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-12 00:00:00 | ||
图片预览

文档简介
一元一次不等式(组)复习课
教学目标:
1.熟练掌握不等式的基本性质。
2.能熟练地解一元一次不等式(组)并能借助数轴确定他们的解集。
3.正确理解不等式(组)的解集,并能利用不等式(组)的解集确定待定字母的值或取值范围。
4.会用一元一次不等式(组)解决实际问题。
教学重点难点:
重点:一元一次不等式(组)及其运用。
难点:用一元一次不等式(组)解决实际问题。
教学过程
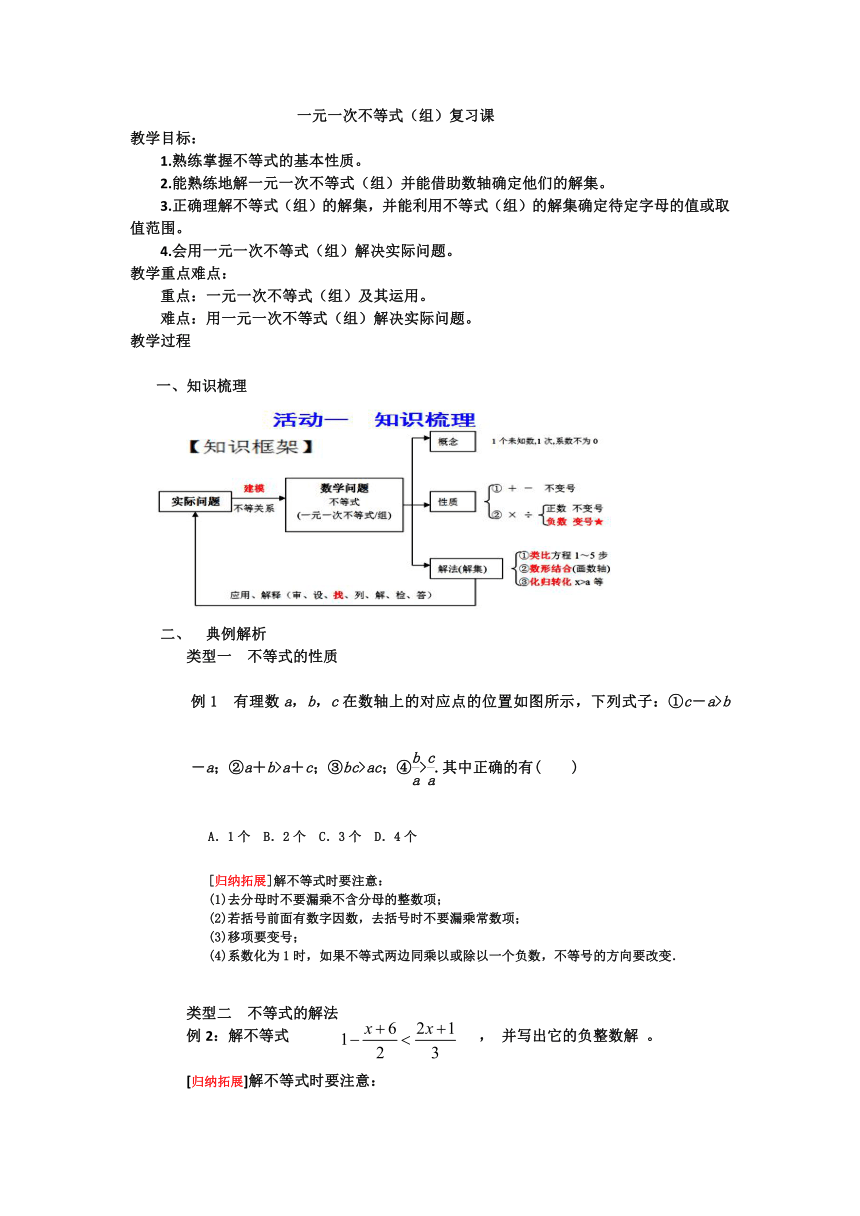
一、知识梳理
二、 典例解析
类型一 不等式的性质
例1 有理数a,b,c在数轴上的对应点的位置如图所示,下列式子:①c-a>b-a;②a+b>a+c;③bc>ac;④>.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
[归纳拓展]解不等式时要注意:
(1)去分母时不要漏乘不含分母的整数项;
(2)若括号前面有数字因数,去括号时不要漏乘常数项;
(3)移项要变号;
(4)系数化为1时,如果不等式两边同乘以或除以一个负数,不等号的方向要改变.
类型二 不等式的解法
例2:解不等式 , 并写出它的负整数解 。
[归纳拓展]解不等式时要注意:
(1)去分母时不要漏乘不含分母的整数项;
(2)若括号前面有数字因数,去括号时不要漏乘常数项;
(3)移项要变号;
(4)系数化为1时,如果不等式两边同乘以或除以一个负数,不等号的方向要改变.
类型三 解不等式组
例3 解不等式组并将它的解集在数轴上表示出来.
[归纳拓展] 确定不等式组的解集有两种方法:
(1)在数轴上表示各不等式的解集,找出公共部分即可.
(2)用口诀:同大取大;同小取小;大小小大取中间;
大大小小找不着(无解).
类型四 求不等式(组)中未知系数的取值范围
例4 若关于x的不等式组的解集为x<2,则a的取值范围是________.
[归纳拓展] 先用含有未知系数a的式子把原不等式组的解集表示出来,然后和已知解集进行比较,最后求出系数a的范围.
类型五 求方程(组)中未知系数的取值范围
例5 已知关于x的方程5x-2m=3x-6m+1的解满足-3类型六 列不等式解应用题
例6:某商场计划购进A,B两种商品,若购进A种商品20件和B种商品15件需380元;若购进A种商品15件和B种商品10件需280元.
(1)A,B两种商品的进价分别是多少元?
(2)若购进A、B两种商品共100件,总费用不超过900
元,则最多能购进A种商品多少件?
(3) 在(2)的条件下,若要求A种商品数量不少于39件,则有哪几种购买方案?选择哪种购买方案购买费用最省?
三、课堂小结
四、作业 见作业纸
教学目标:
1.熟练掌握不等式的基本性质。
2.能熟练地解一元一次不等式(组)并能借助数轴确定他们的解集。
3.正确理解不等式(组)的解集,并能利用不等式(组)的解集确定待定字母的值或取值范围。
4.会用一元一次不等式(组)解决实际问题。
教学重点难点:
重点:一元一次不等式(组)及其运用。
难点:用一元一次不等式(组)解决实际问题。
教学过程
一、知识梳理
二、 典例解析
类型一 不等式的性质
例1 有理数a,b,c在数轴上的对应点的位置如图所示,下列式子:①c-a>b-a;②a+b>a+c;③bc>ac;④>.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
[归纳拓展]解不等式时要注意:
(1)去分母时不要漏乘不含分母的整数项;
(2)若括号前面有数字因数,去括号时不要漏乘常数项;
(3)移项要变号;
(4)系数化为1时,如果不等式两边同乘以或除以一个负数,不等号的方向要改变.
类型二 不等式的解法
例2:解不等式 , 并写出它的负整数解 。
[归纳拓展]解不等式时要注意:
(1)去分母时不要漏乘不含分母的整数项;
(2)若括号前面有数字因数,去括号时不要漏乘常数项;
(3)移项要变号;
(4)系数化为1时,如果不等式两边同乘以或除以一个负数,不等号的方向要改变.
类型三 解不等式组
例3 解不等式组并将它的解集在数轴上表示出来.
[归纳拓展] 确定不等式组的解集有两种方法:
(1)在数轴上表示各不等式的解集,找出公共部分即可.
(2)用口诀:同大取大;同小取小;大小小大取中间;
大大小小找不着(无解).
类型四 求不等式(组)中未知系数的取值范围
例4 若关于x的不等式组的解集为x<2,则a的取值范围是________.
[归纳拓展] 先用含有未知系数a的式子把原不等式组的解集表示出来,然后和已知解集进行比较,最后求出系数a的范围.
类型五 求方程(组)中未知系数的取值范围
例5 已知关于x的方程5x-2m=3x-6m+1的解满足-3
例6:某商场计划购进A,B两种商品,若购进A种商品20件和B种商品15件需380元;若购进A种商品15件和B种商品10件需280元.
(1)A,B两种商品的进价分别是多少元?
(2)若购进A、B两种商品共100件,总费用不超过900
元,则最多能购进A种商品多少件?
(3) 在(2)的条件下,若要求A种商品数量不少于39件,则有哪几种购买方案?选择哪种购买方案购买费用最省?
三、课堂小结
四、作业 见作业纸
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
